主軸熱伸長建模耦合溫度測點優化的研究*

陳 松 王永青 智 瑩 劉子恒

(①遼寧科技大學機械工程與自動化學院, 遼寧 鞍山 114051；②大連理工大學精密與特種加工教育部重點實驗室, 遼寧 大連 116024；③ 鞍山師范學院數學與信息科學學院, 遼寧 鞍山 114205)

數控機床主軸溫度場具有時變性、非平穩性、時滯性等特點，主軸熱伸長也隨著主軸溫度場的變化呈現出非線性與交互關系[1-3]。溫度場信息的準確表達取決于溫度測點布置的準確性[4-5]。通常為確保溫度場信息完整，需要布置冗余溫度測點，以避免熱敏點的遺漏[6]，然而過多的溫度變量易導致主軸熱伸長預測數學模型計算量繁重[7-8]。另外冗余溫度變量的存在導致主軸溫度場熱敏點不明確，熱伸長建模的穩定性與魯棒性受到嚴重影響[9-10]，甚至導致熱伸長預測數學模型出現歧義現象。為提高主軸熱伸長建模魯棒性，要求能夠判定并消除溫度變量的強耦合，從而準確提取主軸溫度場的關鍵溫度測點。然而主軸溫度場的連續分布特性，導致關鍵溫度測點間固有的相關性不易識別與排除。為解決此問題以提高主軸熱伸長建模精度，要求能夠有效地消除主軸溫度場重疊信息，從而建立溫度變量與主軸熱伸長的非線性關系，以達到主軸熱伸長的精準預測的目的。

1 強耦合溫度測點質心聚類

主軸溫度場溫度測點的冗余布置具有隨機性，所以溫度測點的分組結構無法確定，需將溫度測點按照耦合強弱分類以便于關鍵溫度測點的提取。溫度測點溫升值相似度代表溫度測點間的耦合程度。根據溫度測點聚類原則，溫度測點溫升變化程度亦需考慮。為簡化聚類度量標準，利用溫度測點溫升值的距離作為分類的度量方法，距離近的溫度變量分為一類，在不同類中的溫度變量距離較遠。聚類分組后，耦合性強的溫度測點聚類為同一類，變化程度弱的溫度測點聚類為同一類。總結歸納得到主軸溫度場溫度測點優化策略：(1)排除溫度變量強耦合性，保證溫度變量間相關性較弱。(2)保證主軸溫度場信息完整性，適度減少溫度變量數目。(3)選擇影響熱伸長變化程度顯著溫度變量，最大化主軸溫度場信息。(4)量化優化結果與定性分析結果一致。

通過溫度測點的溫升值可以構建溫度變量矩陣T為

其中：m為溫度測點數目；n為溫度測點的溫升測量值樣本數目。T矩陣可視為n維空間中的m個點，可以利用歐氏距離作為溫度變量之間距離的度量標準。設第u個溫度變量為Tu，第v個溫度變量為Tv，Tu與Tv之間的歐氏距離為duv，Tu=(tu1,tu2,…,tun)，Tv=(tv1,tv2,…,tvn)，則：

(1)

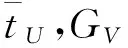
(2)

其中：nU為分類GU的樣本數；nW為分類GW的樣本數；nV為分類GV的樣本數。

以KHC63臥式加工中心主軸熱伸長為研究對象，根據主軸溫度場的分布情況，布置溫度測點，主軸溫度場的溫度測點布置位置如圖1所示。

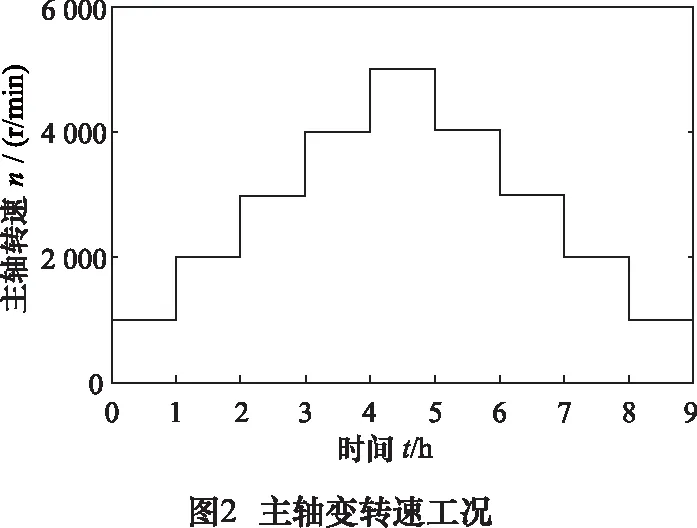
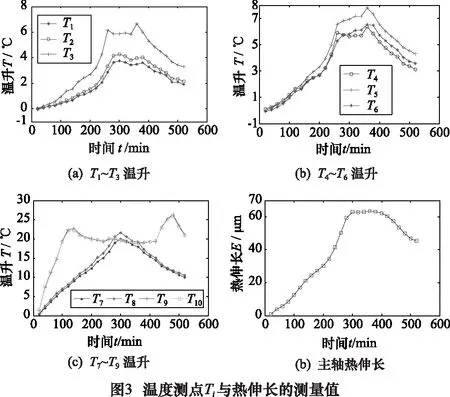
機床初始加工環境溫度為19～21 ℃；針對變轉速工況實驗進行研究，具體工況如圖2所示，空切削運轉，每1分鐘采集各溫度測點溫升與主軸熱伸長1次。溫度變量Ti與主軸熱伸長的實際測量數據如圖3所示，其中i∈N，i∈[1,10]。

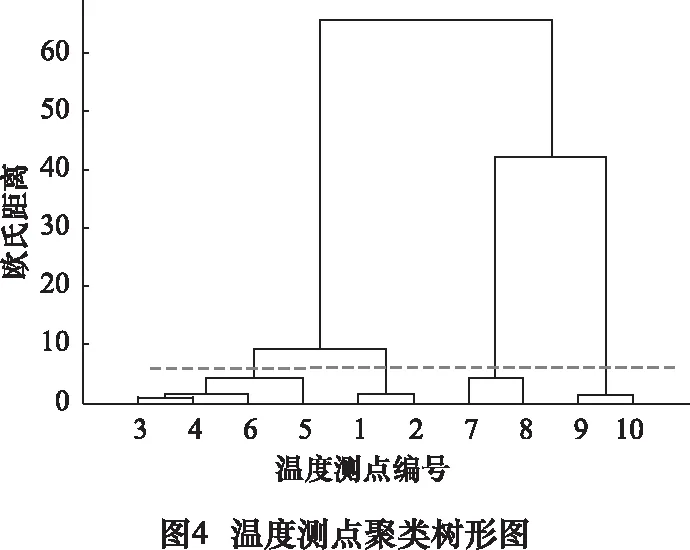
針對此10個初始溫度測點，通過質心聚類分析，生成的溫度測點質心聚類樹形結構如圖4所示。

2 聚類分組關鍵溫度變量灰色關聯分析

因為溫度測點的溫升變化直接影響主軸熱伸長的變化態勢[11]，所以在溫度測點分類內，各溫度測點的溫升與主軸熱伸長的變化態勢的一致性，可作為關鍵溫度測點提取的參考依據。針對溫度測點的溫升變化，有的溫度測點對主軸熱伸長影響程度弱，有的溫度測點對主軸熱伸長影響程度強，所以要求在溫度測點聚類分組內判定出主、次溫度測點，以提取關鍵溫度變量參加主軸熱伸長建模。

設溫度變量Ti為主軸熱伸長的影響因素，數控機床加工的時間序號為j，則Ti在j時刻的溫升測量值為ti(j)。則溫升時間序列為Ti=(ti(1),ti(2),…,ti(n))。主軸熱伸長變化趨勢的數據序列E=(e(1),e(2),…,e(n))。則比較序列Ti相對于參考序列E的灰色關聯系數為：

(3)

其中ζ為分辨系數，ζ∈(0,1)，j=1,2,…,n，i=1,2,…,m，這里ζ取值為0.6。

由于灰色關聯系數反映的關聯信息分散，不利于溫度變量序列之間的整體比較。將溫度變量序列曲線各個時刻的關聯系數進行均值計算得到Ti相對于E的灰色關聯程度，以解決溫度變量序列之間難以比較的問題，灰色關聯度為：

(4)

根據灰色關聯度的規范性，則0<γie1，即主軸溫度場中的溫度變量都與主軸熱伸長相關。R(Ti,E)=1?Ti=E，說明溫度變量序列的灰色關聯度越接近于1，其影響主軸熱伸長的程度越大。將m個關聯度的數值進行降序排序，從而得到溫度變量的灰色關聯序。若R(Tu,E)>R(Tv,E)，則比較序列Tu相對于參考序列E優于Tv，即相對于Tv序列曲線，Tu序列曲線更接近E序列曲線記為Tu>Tv。

根據公式4計算各個溫度變量的灰色關聯度。溫度變量的灰色關聯序的降序排列結果為：T9>T10>T8>T7>T5>T4>T6>T3>T2>T1

根據溫度變量的質心聚類得到4組分類，在同一分類內，依據各溫度變量的灰色關聯度提取關鍵溫度測點。關鍵溫度測點分類提取的結果如表1所示。

表1 關鍵溫度測點提取結果

質心聚類分類結果提取的關鍵溫度測點主軸位置T1T2T2主軸前軸承T3T4T5T6T5主軸箱T7T8T8變速箱T9T10T9主軸電動機

3 關鍵溫度測點相關性的主成分分析

溫度變量強耦合性經過溫度測點優化得以消除，但是關鍵溫度變量間固有的相關性卻難以排除。溫度變量的主成分分析方法采用降低維度技術，將溫度變量轉化為綜合溫度變量，而綜合溫度變量主成分能夠反映絕大部分溫度場信息，同時消除了主軸溫度場的重疊信息。

設綜合溫度變量C為

則綜合溫度變量的矩陣表達形式為：

C=βT

(5)

其中β為主成分系數矩陣。

λ1,λ2,…,λm為β的特征根，λ1≥λ2≥…≥λm>0，所對應的單位特征向量為u1,u2,…,um，有正交陣U=(u1,u2,…,um)，s.t.

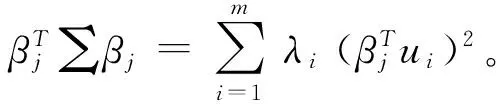
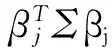
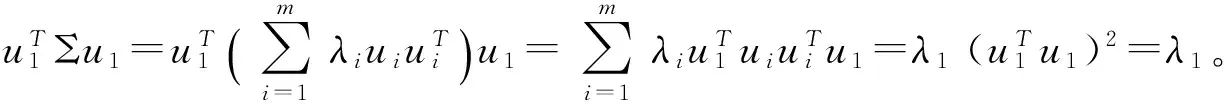
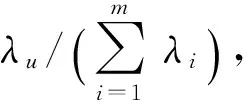
(6)

如果前u個主成分的累計貢獻率達到85%以上，則說明這u個主成分包含了全部的溫度場信息。

溫度變量樣本的協方差矩陣S=[suv]m×m，第u個溫度變量Tu與第v個溫度變量Tv的協方差為：

(7)

利用關鍵溫度變量T2、T5、T8、T9構建T矩陣，計算得到關鍵溫度變量的協方差矩陣S，計算S的特征根與相對應的單位特征向量：λ1=53.13；λ2=15.44；λ3=0.84；λ4=0.02；

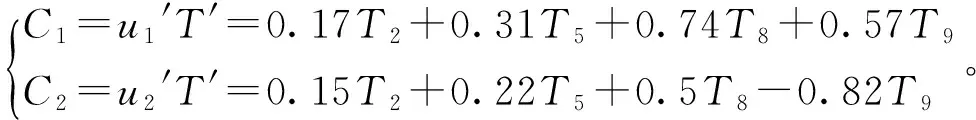
可以看出，經過主成分分析后，原先4維空間數據點的分布在2個維度上得到濃縮，證實了主軸溫度場信息得到簡化處理。

4 基于主成分的最小二乘支持向量機熱伸長建模

最小二乘支持向量機[11]將不等式約束轉換為等式約束，泛化能力強，樣本數量依賴性弱，核函數解決了溫度變量與主軸熱伸長的非線性難以表達問題。

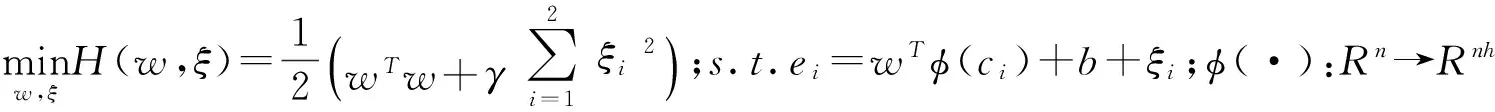
(8)

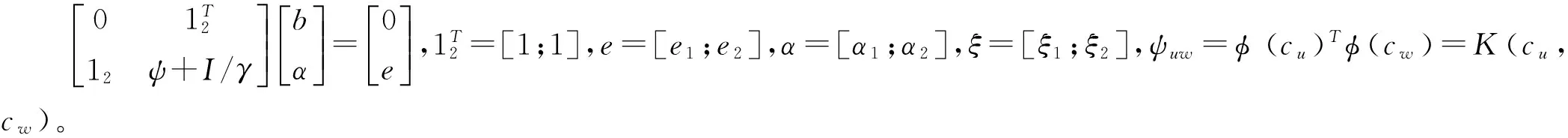
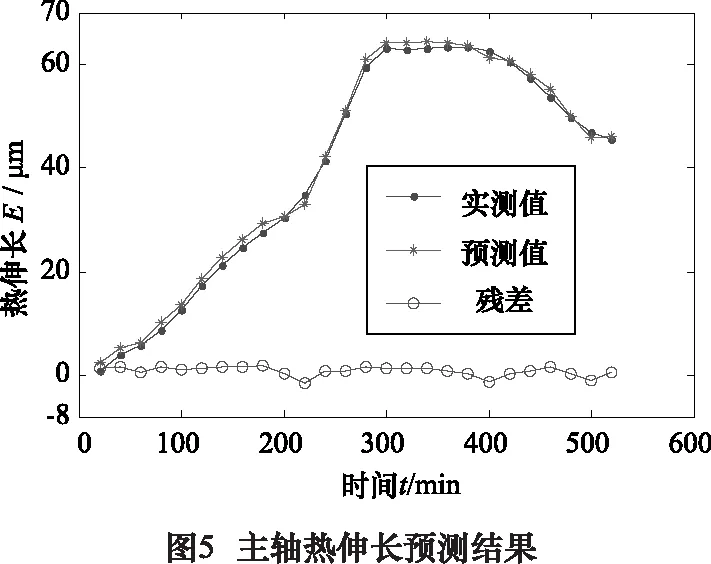
實驗結果表明，變轉速工況條件下，主軸熱伸長達到60 μm以上，預測殘差曲線波動幅度為3 μm以內，證明預測結果可靠，可滿足主軸熱伸長建模精度的要求。

5 結語

通過質心聚類利用歐氏距離為度量手段，聚類強耦合、不顯著變化溫度變量，以溫度變量的灰色關聯序為依據，在同類溫度變量中提取與主軸熱伸長關系緊密的熱敏點，實現了主軸溫度場溫度測點的精簡。基于主成分分析，利用溫度變量的累積貢獻率，降低了關鍵溫度變量維度，進一步簡化了主軸熱伸長的數學建模結構，利用綜合溫度變量的主成分來反映主軸溫度場信息，消除了主軸溫度場的重疊信息，提高了主軸熱伸長建模的魯棒性，基于最小二乘支持向量機的主軸熱伸長預測結果表明關鍵溫度測點判定準確，主軸溫度場關鍵溫度測點耦合信息消除，提高了主軸熱伸長預測模型的可靠性。

[1]李艷, 李英浩, 高峰,等.基于互信息法和改進模糊聚類的溫度測點優化[J].儀器儀表學報, 2015, 36(11):2466-2472.

[2] 羅范杰, 宋丹路.基于逐步線性回歸的溫度測點優化[J].組合機床與自動化加工技術, 2015(3):55-58.

[3] 周杰, 李小汝, 羅范杰.基于FCM自適應模糊聚類的溫度測點優化[J].制造技術與機床, 2015(2):39-42.

[4] Liu Q, Yan J, Pham D T, et al.Identification and optimal selection of temperature-sensitive measuring points of thermal error compensation on a heavy-duty machine tool[J].International Journal of Advanced Manufacturing Technology, 2016, 85(1-4):345-353.

[5] Miao E M, Gong Y Y, Dang L C, et al.Temperature-sensitive point selection of thermal error model of CNC machining center[J].International Journal of Advanced Manufacturing Technology, 2014, 74(5-8):681-691.

[6] Wang Q F, Zhang S, Chen Y, et al.Sensitivity analysis of temperature measuring points for machine tool spindle based on grey system theory[J].Materials Science Forum, 2014, 800-801:720-725.

[7] 黃娟, 肖鐵忠, 李小汝,等.基于模糊C均值聚類算法的溫度測點優化與建模研究[J].機床與液壓, 2015, 43(19):56-58.

[8] 郭前建, 徐汝鋒, 賀磊,等.基于逐步回歸的機床溫度測點優化及熱誤差建模技術[J].制造技術與機床, 2015(12):89-92.

[9] Vyroubal J.Compensation of machine tool thermal deformation in spindle axis direction based on decomposition method[J].Precision Engineering, 2012, 36(1):121-127.

[10] 鄒存建, 舒啟林, 王軍.機床溫度測點布置技術與優化方法的研究[J].工具技術, 2016, 50(10):3-7.

[11] Gao Y, Shan X, Hu Z, et al.Extended compressed tracking via random projection based on MSERs and online LS-SVM learning[J].Pattern Recognition, 2016, 59:245-254.