古建筑木結構榫卯節點剛度的地震損傷分析和識別

薛建陽， 白福玉， 張錫成， 隋 ， 周超鋒

(西安建筑科技大學 土木工程學院，西安 710055)

中國古建筑木結構各構件之間連接主要采用由榫頭和卯孔組成的榫卯節點構造。榫卯節點的剛度變化屬于非線性變化。榫卯節點具有很好的抵抗水平推力作用，能夠有效減少結構的地震響應[1]。強震激勵，榫卯節點張合和榫頭拔出明顯，榫卯節點承載能力下降，榫卯連接柱架層變形增大，結構倒塌危險性較大。在漫長的歷史長河中，由于歷史地震作用影響，榫卯節點松動、拔榫損傷，結構整體抗震性能減弱，結構剩余壽命縮短。確立榫卯節點的損傷剛度和提前辨識剛度參數，對古建筑損傷評估和維修保護具有重要指導意義。

王曉燕等[2]采用最小二乘和擴展卡爾曼濾波方法反演系統地震載荷和識別結構動態參數。何浩祥等[3]用靜動力凝聚和擴展卡爾曼濾波對連續梁進行了剛度和阻尼損傷識別。趙博宇等[4]完成了擴展卡爾曼濾波算法對在噪聲較大環境下的結構質量、阻尼和剛度識別，更新了長期不確定振動臺模型。王鑫等[5]對隨機激勵作用下的古木結構梁上各節點的加速度響應信號進行小波包分解，提出了小波包能量曲率差損傷識別指標，通過此指標進行古木結構的損傷識別。Weng等[6]提出了識別節點模態參數的子空間、有限元模型修正和非線性最小二乘結合的方法，這種方法識別過程耗時。Wu等[7]提出了加權最小二乘和貝葉斯結合的方法；Xu等[8]提出了節點損傷指數和二階特征靈敏度近似方法。刁延松等[9]利用振動傳遞率函數和統計假設檢驗對海洋平臺結構進行了損傷識別研究。鄭澤棟等[10]利用結構響應功率譜密度函數對結構損傷參數的靈敏度實現結構損傷識別。羅鈞等[11]根據單元損傷系數方程和約束線性最小二乘法對剪切型框架結構損傷進行了定位和定量識別。

本文根據西安建筑科技大學古建筑抗震課題組1∶3.52殿堂式古建筑木結構振動臺試驗模型，建立了結構簡化力學模型，推導了結構狀態方程和觀測方程。振動臺試驗確定了地震作用下榫卯節點剛度損傷演化規律，利用靜動力凝聚方法建立了結構剛度與榫卯節點剛度之間關系。進行了力錘敲擊測試試驗和仿真計算，獲得了結構柱架層和乳栿層位移、速度和加速度響應。考慮噪信比5%噪聲干擾，利用偏最小二乘和擴展卡爾曼濾波方法對榫卯節點轉動剛度進行了損傷識別。結果表明，基于偏最小二乘、擴展卡爾曼濾波和靜動力凝聚方法對榫卯節點轉動剛度識別精度較高，具有較好適用性。

1 結構狀態方程和觀測方程

1.1 結構簡化力學模型

忽略結構空間平扭耦合作用，根據西安建筑科技大學古建筑抗震課題組1∶3.52殿堂式古建筑木結構振動臺試驗設計模型，選取其一榀構架為研究對象，建立平面簡化力學模型，如圖1所示。模型立柱與額枋榫卯連接用彈簧單元模擬，梁柱及斗拱用梁單元模擬，將結構每個區域質量分別集中于榫卯連接柱架層和乳栿層處。

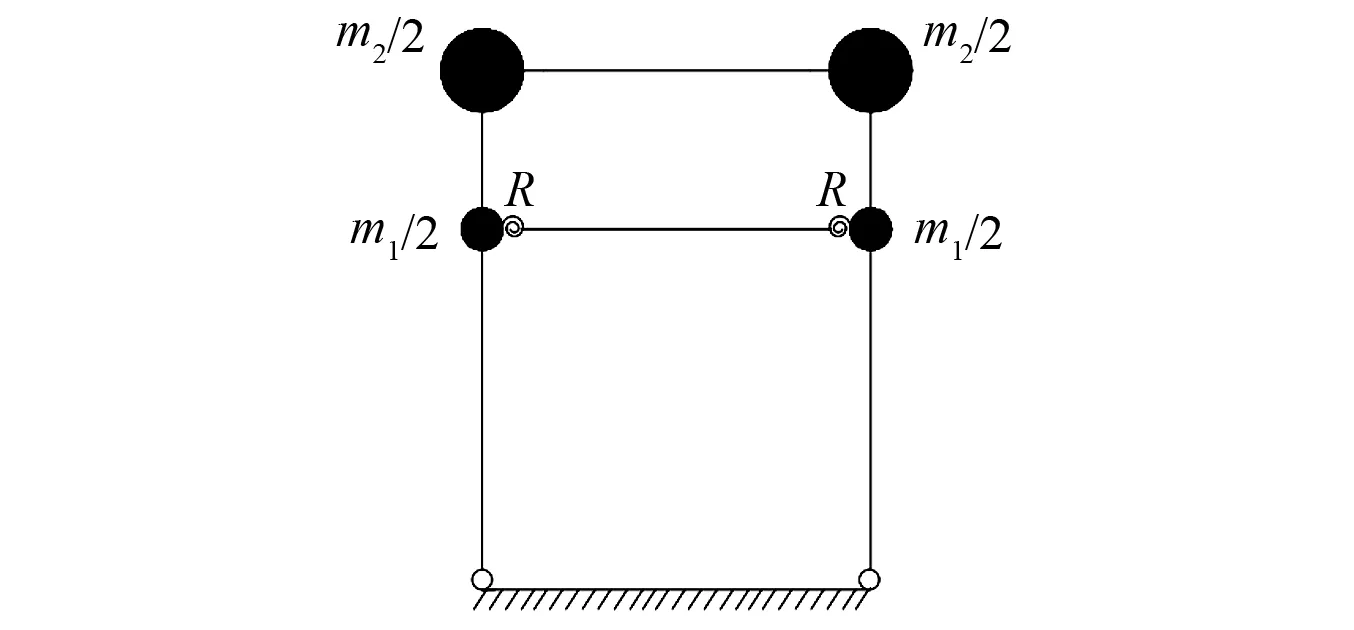
圖1 平面簡化力學模型Fig.1 The simplified mechanical model of timber structure

1.2 結構動力方程

(1)

設木材順紋抗彎彈性模量為E，梁枋截面慣性矩為IB、額枋截面慣性矩為IL、立柱截面慣性矩為IC，斗拱等效抗彎剛度為EIC，榫卯節點轉動剛度為R，立柱高度為h1，斗拱鋪作層高度為h2，額枋和梁枋跨度為L，半剛性系數為μ。忽略梁柱軸向變形，考慮榫卯節點半剛性連接特性，根據Chopra等[12]給出的兩端半剛性連接桿件、一端鉸接一端固定桿件的剛度矩陣，組裝確定結構整體剛度矩陣[K]各元素

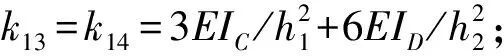
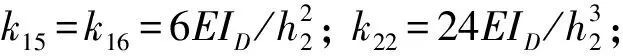
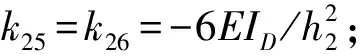
k33=k44=3EIC/h1+(4+12μ)EIL/(R*L)+4EID/h2;

k34=2EIL/(R*L)；

k35=2EID/h2;k36=0,k45=0；

k46=2EID/h2;k56=2EIB/L;

k55=k66=4EIB/L+4EID/h2;μ=EIL/(RL);

R*=1+8μ+12μ2。

1.3 結構狀態方程和觀測方程

動力方程分塊形式為

(2)

利用靜動力凝聚法，消除具有零質量轉動項，凝聚后結構動力方程為

(3)

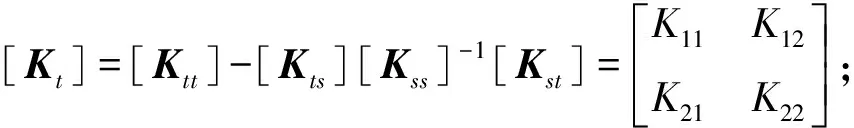
將動力方程式(3)轉化為狀態方程

(4)

令結構柱架層和乳栿層平動速度δ3、δ4，將結構剛度K11、K12(K21)、K22，阻尼比ζ和結構固有頻率ω看成結構的5個狀態向量，結構狀態方程

(5)

設結構量測值分別為Z1、Z2，結構觀測方程

(6)

2 剛度識別方法

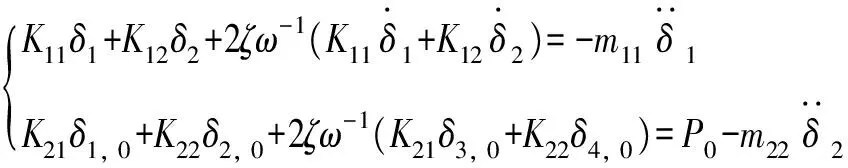
觀測柱架層和乳栿層位移、速度和加速度響應；獲得觀測矩陣H、剛度參數X、量測Z為

X=[K11K12K22]T

(8)

首先基于奇異值分解的偏最小二乘法(PLS-SVD)計算步驟如下：

步驟1H和Z進行標準化得到H0和Z0；

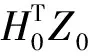
步驟3 計算H0的潛變量矩陣T和Z0的潛變量矩陣U，其中T=H0W，U=Z0C。

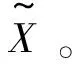
擴展卡爾曼濾波是用遞推狀態空間方程一階泰勒公式進行估計的一種方法，適用剪切型結構體系參數識別。質量已知的剪切型結構體系，擴展卡爾曼濾波估計公式[13]為

(9)

式中：R為觀測噪聲；P為誤差協方差矩陣；Φ為狀態轉移矩陣；G為增益矩陣。

狀態轉移矩陣為

(10)

式中：A為狀態雅可比矩陣；H為觀測雅可比矩陣；I為單位矩陣；Δt為采樣時間間隔。

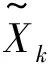
3 榫卯節點剛度損傷分析

為了研究古建筑木結構榫卯節點剛度在地震下的累積損傷，課題組制作了一個縮尺比為1∶3.52單層單開間殿堂結構當心間梁柱燕尾榫榫卯連接模型，如圖2所示，模型上面嵌固配重為14 kN/m2的鋼筋混凝土板作為等效屋蓋荷載，4塊柱礎固定在2.0 m×2.2 m的振動臺上。試驗中分別在臺面、柱腳、柱頂和乳栿處布置磁電式位移傳感器、磁電式速度傳感器和差容式加速度傳感器。對模型分別輸入50 gal、75 gal、100 gal、150 gal、200 gal、300 gal的El Centro波、Taft波、蘭州波，400 gal、500 gal、600 gal、800 gal、900 gal的El Centro地震波，獲得模型柱腳、柱架層、乳栿層在不同損傷工況下的位移、速度和加速度響應。

圖2 古建筑木結構振動臺試驗Fig.2 Shaking table test of ancient timber building

試驗表明，隨著地震作用增加，柱架層最大側移和榫頭拔出量越來越大，直至榫頭劈裂和卯口破壞，結構模型倒塌。當地震輸入小于150 gal時，榫卯節點轉動

不明顯；地震輸入200 gal時，榫卯節點轉動幅度較小，未出現拔榫；當地震輸入達300 gal時，柱架層最大側移28.28 mm，榫頭拔出量約為3 mm；如圖3所示；當輸入激勵達600 gal時，柱架層最大側移56.782 mm，榫頭拔出量約為8 mm。

圖3 試驗現象Fig.3 The test phenomenon

根據加載過程榫卯節點轉動幅度，定義工況1為震前無損工況，工況2為200 gal地震加載完時刻工況，工況3為300 gal地震加載完時刻工況，工況4為600 gal El Centro波加載完時刻損傷工況。各工況榫卯節點的滯回曲線如圖4所示。

圖4 不同工況下榫卯節點的滯回曲線Fig.4 The moment-rotation curve of the node under different conditions

根據滯回曲線擬合榫卯節點的骨架曲線，確定各工況下榫卯節點的割線剛度如圖5所示，工況3的榫卯節點剛度損傷最大，初始剛度只有工況1的23.19%，屈服剛度只有工況1的11.31%；而工況4初始剛度較工況3增大；增大48.32%，屈服剛度較工況3減小，減小29.95%。說明隨著地震作用累積增加，榫頭從卯口拔出，榫頭受卯口擠壓加劇，榫卯節點初始剛度損傷程度先增大后減小，屈服剛度損傷程度一直增大。

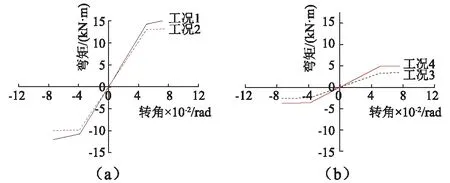
圖5 不同工況榫卯節點割線剛度Fig.5 The secant stiffness of the node under different conditions

各工況榫卯節點轉動剛度如表1所示。地震前榫卯節點初始剛度279.8 kN·m/rad、地震后榫卯節點初始剛度最小為64.88 kN·m/rad，發現榫卯節點初始剛度變化范圍與不同松動程度下古建筑燕尾榫節點初始剛度試驗[14]50～300 kN·m/rad的范圍基本一致，說明了地震前后榫卯節點初始轉動剛度試驗結果的準確性。

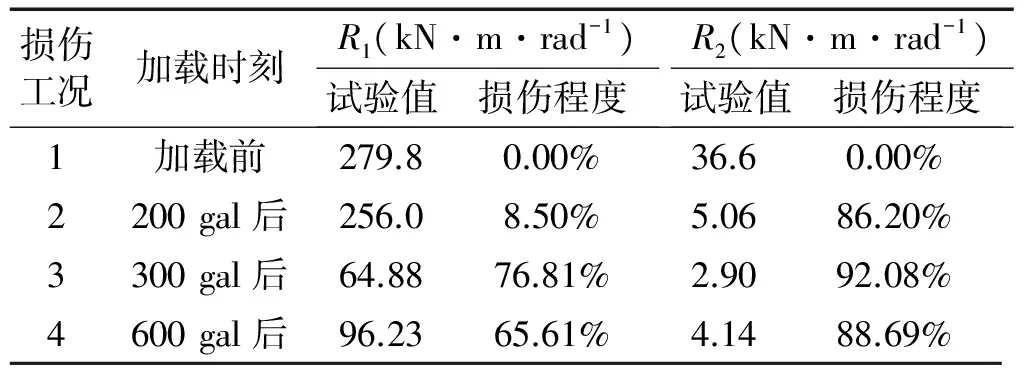
表1 不同工況下榫卯節點割線剛度值

根據靜動力凝聚方法，獲得了結構剛度參數K11與榫卯節點初始剛度R1近似關系，如圖6所示，四種工況剛度參數K11試驗值分別為107.99 kN/m、107.47 kN/m、102.87 kN/m、103.67 kN/m。

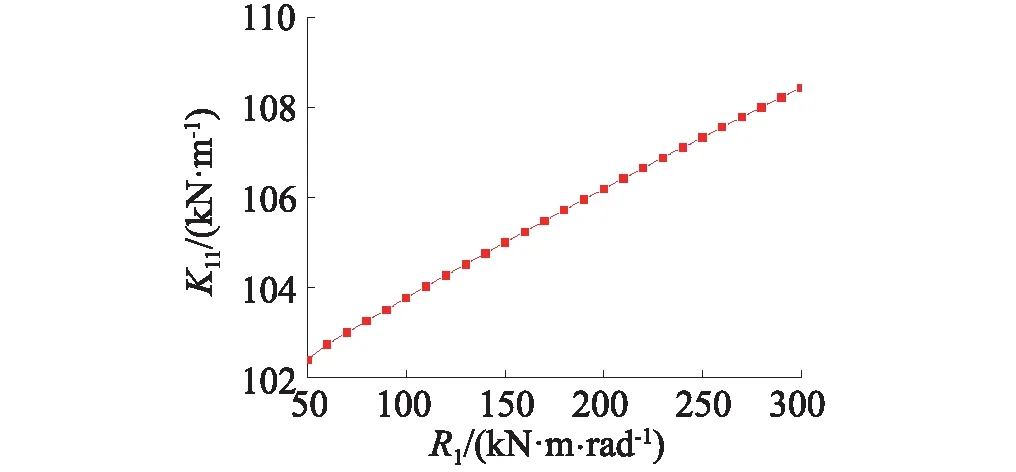
圖6 結構剛度K11和節點剛度R1的關系Fig.6 Relationship between structural layer stiffness K11 and node stiffness R1

西安建筑科技大學古建筑課題組根據榫卯連接模型低周反復荷載試驗，擬合榫卯節點恢復力模型，獲得了榫卯節點初始剛度和屈服剛度呈一定的比例關系[15]。根據各工況榫卯節點割線剛度R1和R2，得到屈服前后割線剛度比例系數。如表2所示。

表2 R2和R1的比值

4 仿真算例

根據試驗模型建立仿真模型，如圖7所示。柱、額枋和梁枋用三維線性兩節點單元模擬；柱與額枋榫卯連接用非線性轉動彈簧單元模擬，柱腳與礎石滑移連

接用軸向彈簧、阻尼器、間隙單元及滑動器構成組合單元模擬，斗拱用水平和豎向的彈簧-阻尼器單元模擬，連接彈簧單元和阻尼器假定為無質量和尺寸。屋蓋質量等效到乳栿相交四個節點上，用2D單元模擬。模型材料密度為550 kg/m3，材料順紋抗彎彈性模量為67.27 MPa，榫卯節點剛度根據表1定義，斗拱水平抗側剛度、豎向抗壓剛度由低周反復荷載試驗[16]和豎向承載力試驗[17]測得，柱腳與礎石的滑動摩擦系數取為0.4，四種工況下有限元仿真計算采用的阻尼比例系數從振動臺試驗獲得，分別為0.029、0.035、0.039和0.044。

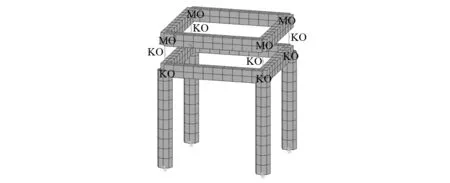
圖7 木構架有限元模型Fig.7 Finite element model of wooden building

由圖8可以看出，柱腳、榫卯連接柱架層和乳栿層加速度時程響應曲線基本吻合，峰值出現的時刻和大小基本相同。由于仿真模型中未完全模擬榫卯節點的滯回關系，致使響應曲線形狀和走向略有不同。無損工況下仿真模型自振頻率為1.88 Hz，與試驗獲得的一階自振頻率2.05 Hz比較，相對誤差為8.29%。由此可以說明，仿真模型可滿足計算精度要求。

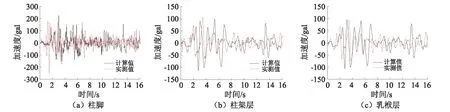
圖8 加速度時程曲線Fig.8 The time history curve of the acceleration

圖9選取前6階自振頻率比較，發現隨節點損傷程度增加，前3階頻率變化較大，后3階頻率沒有變化。仿真計算振型結果顯示，第一階振型和第二階振型為平動，第三階振型為結構的整體扭轉，第四階～第六階振型表現為斗拱的豎向振動。由于累積地震作用，榫卯節點剛度損傷變小，木結構層間水平和豎向剛度損傷均變化明顯，結構前3階自振頻率對應的振型變化明顯。說明由于榫卯節點剛度損傷對結構低頻振型敏感，計算中應選取低頻部分的響應作為剛度識別主要依據。

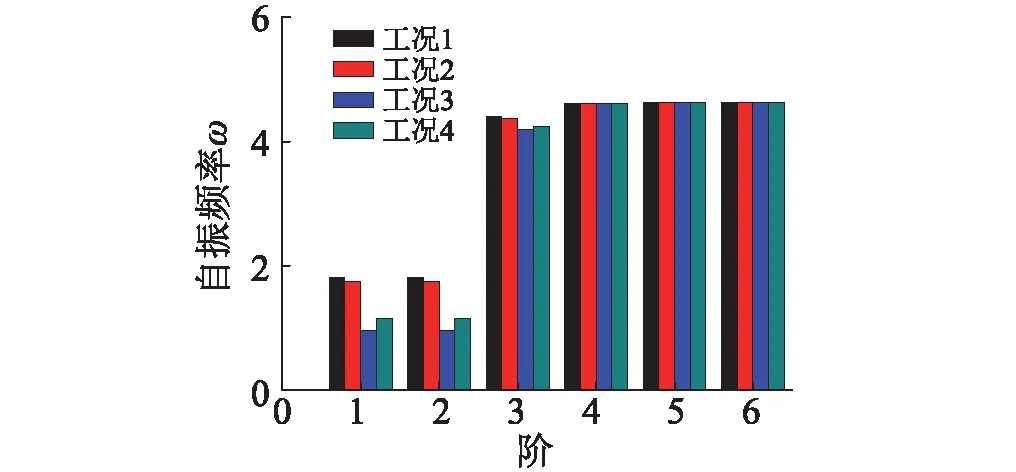
圖9 不同損傷下工況結構自振頻率 Fig.9 Natural frequency of different damage simulation model

仿真模擬了脈沖力錘錘擊木結構上混凝土配重塊，使結構產生微振動響應進行測試。忽略脈沖力錘的質量影響，脈沖激勵如圖10所示，由于實際施加脈沖激勵時間很短，仿真計算中激勵時間取為0.2 s，結構位移、速度和加速度響應采樣時間設為10 s，時間步長為0.009 8 s。

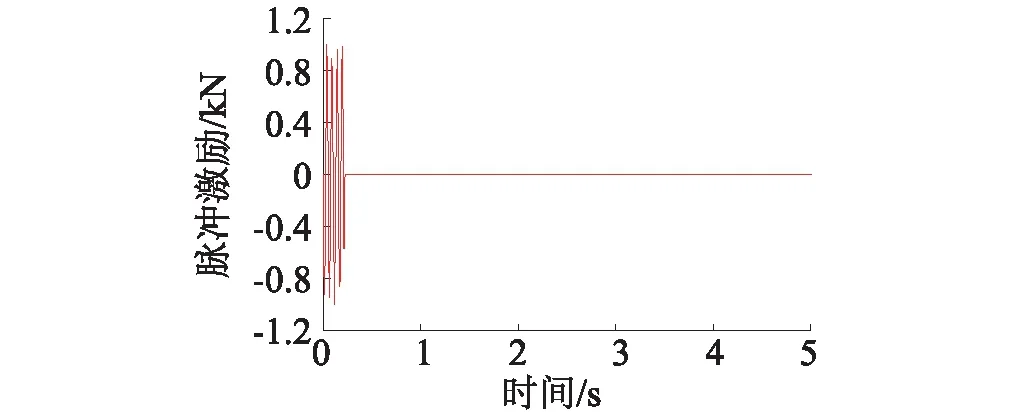
圖10 脈沖激勵Fig.10 Pulsed excitation

比較不同損傷工況柱架層位移、速度和加速度響應發現，各工況最大負位移-0.238 mm、-0.24 mm、-0.286 mm、-0.263 mm，出現時刻為0.107 s、0.107 s、0.205 s、0.205 s；最大正位移0.204 mm、0.209 mm、0.11 6mm、0.132 mm，出現時刻為0.420 s、0.430 s、0.701 s、0.520 s。

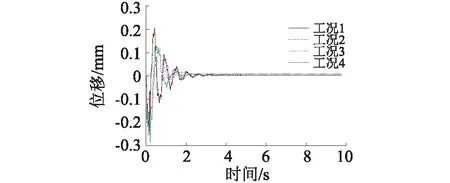
圖11 各工況榫卯連接柱架層位移響應Fig.11 The time history curve of the column top under different conditions

圖11說明：隨榫卯節點剛度損傷加劇，柱架層負位移峰值增大，正位移峰值減小；工況3較工況1負位移峰值增大4.8%，正位移峰值減小35.3%，負位移峰值時間延后0.102 s，正位移峰值時間延后0.281 s。四種工況下結構的位移和速度響應在4 s后都基本趨于平穩。

5 榫卯節點剛度損傷識別

各工況質量矩陣中：m11=250 kg，m22=3 600 kg；各工況剛度矩陣為

剛度矩陣上標代表不同損傷工況，剛度單位為kN/m。假定阻尼比例系數已知，采樣點數取100個。在無噪聲干擾下，利用觀測得到的榫卯連接層位移、速度、加速度響應組裝觀測矩陣和量測值，反演計算中觀測矩陣呈病態性，對其進行奇異值分解，選取奇異值分解階次為2，分離階數為1，利用偏最小二乘初步估計各工況剛度參數。

無干擾下，偏最小二乘法估計各工況K11的收斂曲線如圖12所示，若設error為相對誤差，則各工況K11識別值與真實值相對誤差均為0%。

error=(識別值-真實值)/真實值×100%

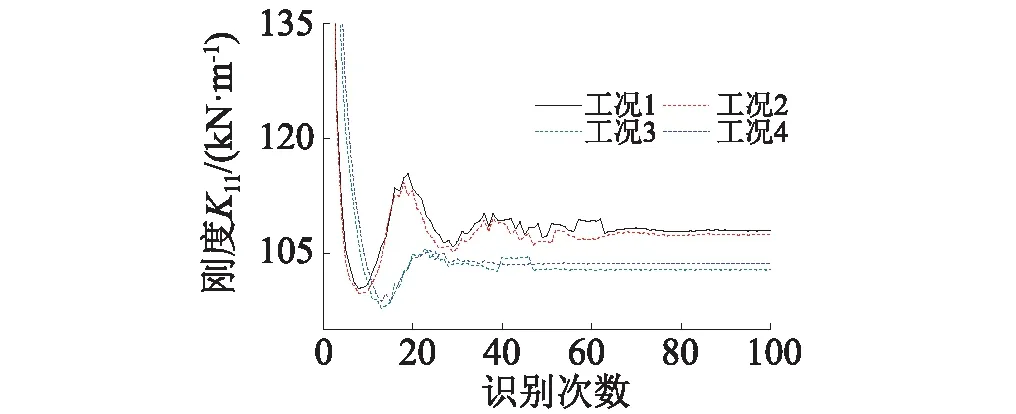
圖12 噪信比為0%時各工況的K11收斂曲線Fig.12 The convergence curves of K11 under different conditions with the noise-signal ratio 0%

在力錘敲擊測試模型響應中，根據輸出噪聲均方根與不含噪純信號均方根之比，確定各階段噪信的比值約為5%。因此，模擬計算中在觀測位移、速度和加速度響應中加入了噪信比為5%的高斯隨機噪聲。設定參數收斂區域K11識別值上限為108 kN/m，下限為102 kN/m，剔除識別結果中的超限不合理數據。四種工況剛度K11整體收斂性均較好，K11識別值分別為107.91 kN/m、107.35 kN/m、102.77 kN/m和103.57 kN/m，識別值與真實值相對誤差分別為-0.15%、-0.11%、-0.1%、-0.1%。

在近似估計基礎上，以上述近似識別值為初值，給定初始協方差和量測值，利用擴展卡爾曼濾波方法識別各工況結構剛度K11結果如圖13和表3所示。

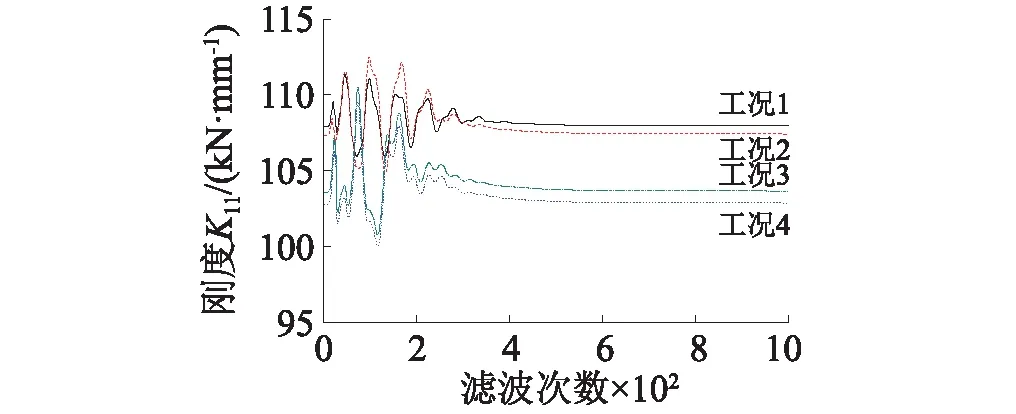
圖13 噪信比5%時各工況的K11收斂曲線Fig.13 The convergence curves of K11 under different conditions with the noise-signal ratio 5%

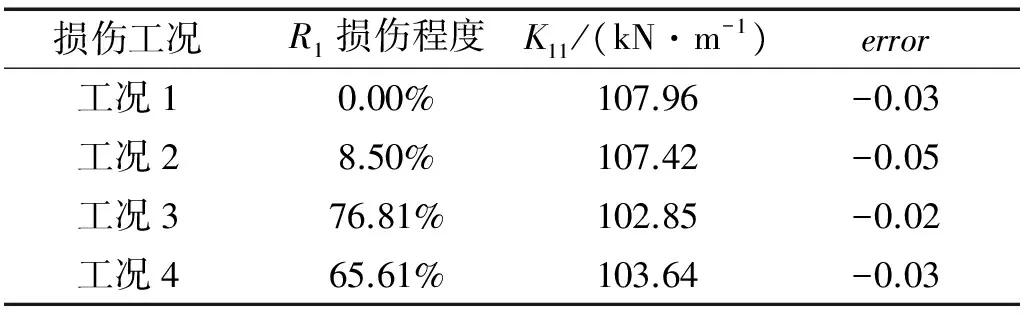
損傷工況R1損傷程度K11/(kN·m-1)error工況10．00%107．96-0．03工況28．50%107．42-0．05工況376．81%102．85-0．02工況465．61%103．64-0．03

榫卯連接柱架層水平位移識別如圖14所示，三種工況下柱架層水平位移識別值和真實值時程軌跡吻合較好，說明結構剛度K11識別效果較好。

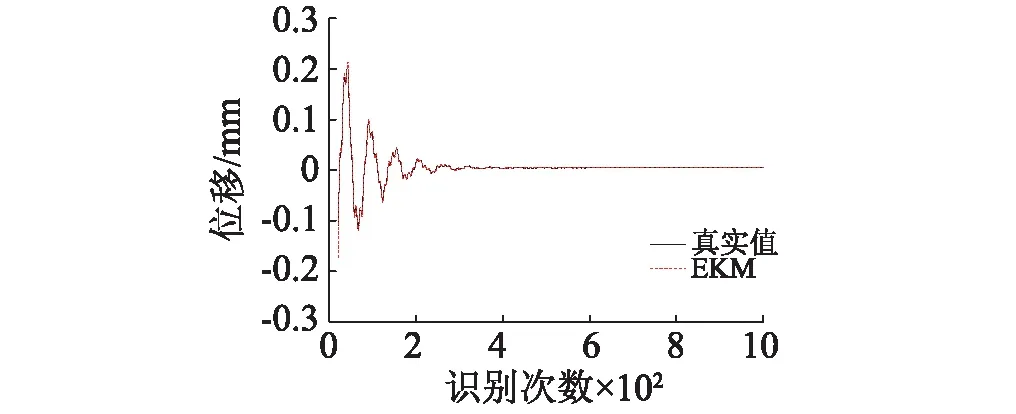
圖14 工況1時柱架層位移識別值與真實值的比較Fig.14 The comparison between identification value and test value of the column top displacement under 1st loading condition

由結構剛度參數K11與R1關系線性插值計算，進一步確定榫卯節點初始剛度R1識別值，再根據榫卯節點屈服前后剛度比例系數，確定R2損傷識別值。表4結果表明，脈沖激勵下靜動力凝聚、偏最小二乘和擴展卡爾曼濾波的混合算法能夠根據結構位移和速度響應對榫卯節點剛度進行損傷識別，識別結果精度較高，穩定性較好，具有較好的適用性；隨榫卯節點地震損傷增加，初始剛度和屈服剛度識別值與試驗值相對偏差增大。

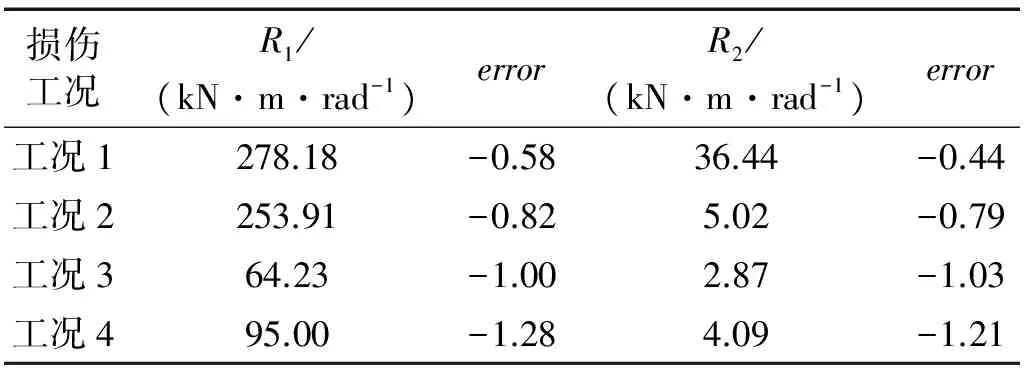
表4 榫卯節點剛度識別值

6 結 論

本文在西安建筑科技大學古建筑木結構振動臺試驗基礎上，研究了古建筑木結構榫卯節點剛度地震累積損傷規律。基于榫卯連接木結構簡化力學模型，采用靜動力凝聚方法建立了結構剛度與榫卯節點剛度之間關系，推導出結構狀態方程和觀測方程，采用PLS-SVD和擴展卡爾曼濾波方法研究了榫卯節點地震累積損傷識別，得到以下結論：

(1) 隨著結構累積損傷加劇，榫頭從卯口拔出，榫頭受卯口擠壓加劇，榫卯節點屈服剛度損傷一直增加，榫卯節點初始剛度損傷先增大后減小。

(2) 榫卯節點損傷對低階頻率部分的振型敏感。隨著榫卯節點地震損傷增加，力錘激勵達峰值點所用時間越來越短；柱頭、柱腳、乳栿的位移和速度最大峰值越來越大。

(3) 在噪信比5%的噪聲干擾下，古建筑木結構損傷識別結果表明，靜動力凝聚、偏最小二乘和擴展卡爾曼濾波的混合算法能定量識別木結構剛度損傷程度，識別精度較高。

(4) 根據靜動力凝聚前后剛度矩陣可以準確建立榫卯節點屈服前剛度與結構剛度參數比例關系，結合各工況榫卯節點屈服前后剛度比，可以確定榫卯節點屈服前后割線剛度損傷識別值。

(5) 僅在結構某一位置施加脈沖激勵實際操作更簡單，識別結果穩定性和適用性較好。力錘敲擊的人工激勵獲取微振動響應方法可以在識別榫卯節點剛度參數中應用。

[ 1 ] 薛建陽, 趙鴻鐵, 張鵬程. 中國古建筑木結構模型的振動臺試驗研究[J]. 土木工程學報, 2004, 37(6): 6-11.

XUE Jianyang, ZHAO Hongtie, ZHANG Pengcheng. Study on the seismic behaviors of chinese ancient woodn buolding by shaking table test [J]. China Civil Engineering Journal, 2004, 37(6): 6-11.

[ 2 ] 王曉燕,黃維平,李華軍. 地震動反演及結構參數識別的EKF算法[J]. 工程力學, 2005, 22(4): 20-23.

WANG Xiaoyan, HUANG Weiping, LI Huajun. Inversion of ground motion and identification of structural parametersby EKF [J]. Engineering Mechanics, 2005, 22(4): 20-23.

[ 3 ] 何浩祥, 呂永偉, 韓恩圳. 基于靜動力凝聚及擴展卡爾曼濾波連續梁橋損傷識別[J]. 工程力學, 2015, 32(7): 156-163.

HE Haoxiang, Lü Yongwei, HAN Enzhen. Damage detection for continuous girder bridge based on static-dynamic condensation and EKF [J]. Engineering Mechanics, 2015, 32(7): 156-163.

[ 4 ] 趙博宇,丁勇, 吳斌. 基于擴展卡爾曼估計算法的地震模擬振動臺模型識別[J]. 振動與沖擊, 2014, 33(12): 145-

150.

ZHAO Boyu, DING Yong, WU Bin. Identification of shaking table model for seismic simulation based on an extended Kalman estimator [J]. Journal of Vibration and Shock, 2014, 33(12): 145-150.

[ 5 ] 王鑫, 胡衛兵, 孟昭博. 基于小波包能量曲率差的古木結構損傷識別[J]. 振動與沖擊, 2014, 33(7): 153-159.

WANG Xin, HU Weibing, MENG Zhaobo. Damage detection of an ancient wood structure based on wavelet packet energy curvature difference [J]. Journal of Vibration and Shock, 2014, 33(7): 153-159.

[ 6 ] WENG J H, LOH C H,YANG J N. Experimental study of damage detection by data-driven subspace identification and finite-element model updating [J]. Journal of Structural Engineering, 2009, 15(12): 1533-1544.

[ 7 ] WU J R, LI Q S. Structural parameter identification and damage detection for a steel structure using a two-stage finite element model updating method [J]. Journal of Constructional Steel Research, 2006, 62: 231-239.

[ 8 ] XU Longhe, LI Zhongxian, QIAN Jianru. Test analysis of detection of damage to a complicated spatial model structure [J]. Acta Mechanica Sinica, 2011, 27(3): 399-405.

[ 9 ] 刁延松, 徐東鋒, 徐菁,等. 基于振動傳遞率函數與統計假設檢驗的海洋平臺結構損傷識別研究[J]. 振動與沖擊, 2016,35(2): 218-222.

DIAO Yansong, XU Dongfeng, XU Jing, et al. Structural damage identification of offshore platform based on the vibration transmissibility function and statistical hypothesis testing [J] . Journal of Vibration and Shock, 2016, 35(2): 218-222.

[10] 鄭澤棟, 陳偉歡, 呂中榮, 等. 基于功率譜靈敏度分析的結構損傷識別方法[J]. 振動與沖擊, 2014,33(12): 76-79.

ZHENG Zedong, CHEN Weihuan, Lü Zhongrong, et al. Structural damage identification based on sensitivity analysis of power spectral density [J] . Journal of Vibration and Shock, 2014, 33(12): 76-79.

[11] 羅鈞, 劉綱,黃宗明. 基于約束最小二乘法的剪切型框架結構損傷識別新方法[J]. 振動與沖擊, 2016, 35(20): 119-124.

LUO Jun, LIU Gang, HUANG Zongming. Damage detection for a shear frame structure based on the constrained least squares method [J] . Journal of Vibration and Shock, 2016, 35(20): 119-124.

[12] CHOPRA A K, NAEIM F. Dynamics of structures: theory and applications to earthquake engineering[M]. 3rd ed. New Jersey: Pearson Prentice Hall, 2007.

[13] 李國強, 李杰. 工程結構動力檢測理論與應用[M] . 北京: 科學出版社, 2002.

[14] 薛建陽,李義柱,夏海倫,等. 不同松動程度的古建筑燕尾榫節點抗震性能試驗研究[J]. 建筑結構學報, 2016, 37(4): 73-79.

XUE Jianyang, LI Yizhu, XIA Hailun, et al. Experimental study on seismic performance of dovetail joints with different loose degrees in ancient buildings [J]. Journal of Buiding Structures, 2016, 37(4): 73-79.

[15] 姚侃, 趙鴻鐵, 葛鴻鵬. 古建木結構榫卯連接特性的試驗研究[J]. 工程力學, 2006, 23 (10) : 168-173.

YAO Kan, ZHAO Hongtie, GE Hongpeng. Experimental studies on the characteristic of mortise-tenon joint in historic timber buildings [J]. Engineering Mchanics, 2006, 23(10): 168-173.

SUI Yan, ZHAO Hongtie, XUE Jianyang, et al. Experimental study on lateral stiffness of dougong layer in chinese historic buildings [J]. Engineering Mchanics, 2010, 27(3): 74-78 .

[17] 高大峰,趙鴻鐵,薛建陽. 中國木結構古建筑的結構及其抗震性能研究[M]. 北京: 科學出版社, 2008.