由兩道壓軸題談高中數學的核心素養

廖前愛

洪湖市教研室 湖北洪湖 433200

新課改的一個重要理念就是提出了學科的核心素養，對核心素養的理解可能會仁者見仁，智者見智，作為一名在教學一線工作二十多年的教師，我認為最重要的核心素養是：遇到沒教過的問題，會用已教過的知識去解決。

下面筆者就2016全國高考I卷（文科）和2017年全國高考I卷（理科）的壓軸題（這兩道題都是雙零點問題）談談我對數學核心素養的拙見。

（2016全國高考I卷（文科））已知函數f(x)=(x-2)ex+(x-1)2。

(Ⅰ)討論 f(x)的單調性；

(Ⅱ)若f(x)有兩個零點，求a的取值范圍。

第(Ⅰ)問考查的是函數單調性與導數的關系，

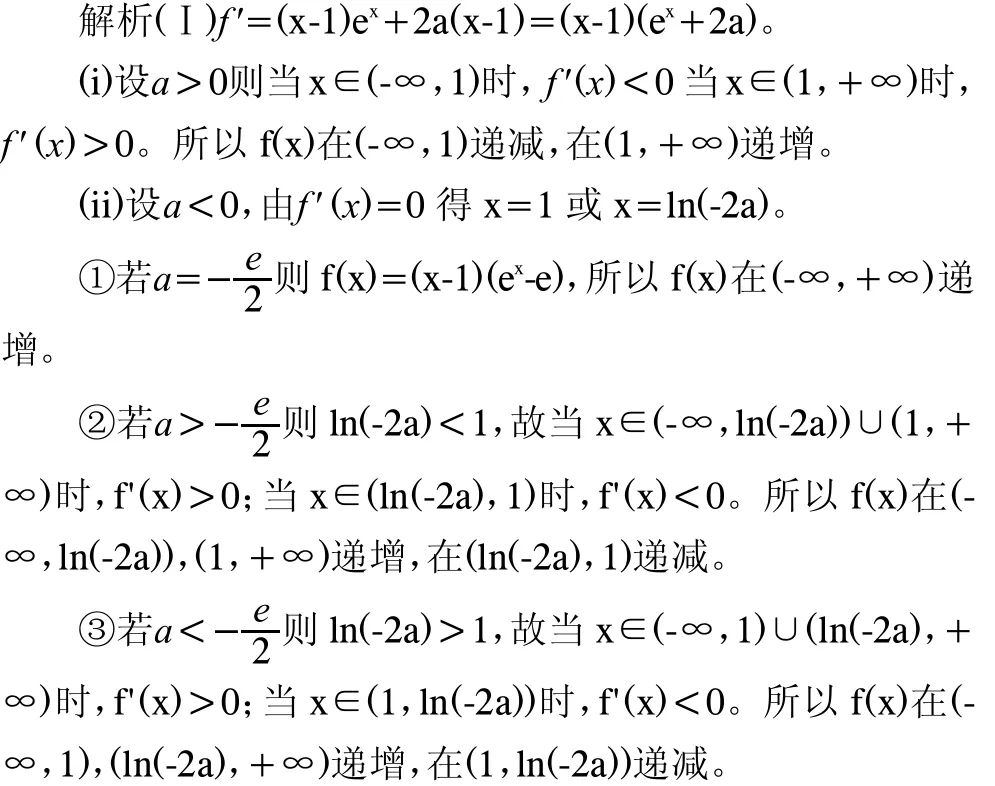
第(Ⅱ)問考查函數零點，我們知道：如果函數f(x)在區間[a，b]上連續，且 f(a)f(b)＜0，那么函數 f(x)在區間（a，b）內有零點。但是如何找到零點所在區間或者說明零點的存在性則是題目的重點，也是難點。下面先看標答：

(Ⅱ)(i)設a＜0，則由(Ⅰ)知，f(x)在(-∞，1)遞減，在(1，+∞)遞增。

(ii)設a=0，則 f(x)=(x-2)ex，所以 f(x)只有一個零點。

其實這類題型的核心素養是利用放縮找點，只要說明零點的存在即可，這樣就有了放縮的多樣性。

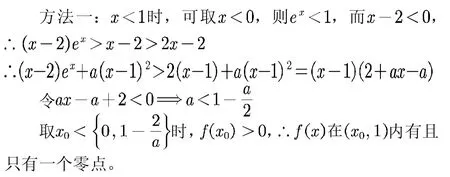
綜上，a＞0時f x有兩個零點。

這種方法先把礙眼的ex放縮掉，再對一次式進行放縮至能提取公因式，不至于用求根公式求出一個很丑的根來。

方法二：

綜上，a＞0時（f x）有兩個零點。

這種方法中10086是一種趣向，可以理解為“在那遙遠的地方”，是一種動態找點，我們可以根據自己的喜好任取一個數（如5201314），這種方法恰恰把握了這類題型的本質特點，也讓我們發現數學之美的數學之趣。

當然本題第(Ⅱ)問也可以用分離參數法，

下面我們再看看2017年全國高考I卷（理科）的壓軸題：

f(x)在R上遞減；

②當a>0時，令f`(x)＝0，從而aex-1＝0得x＝-lna。

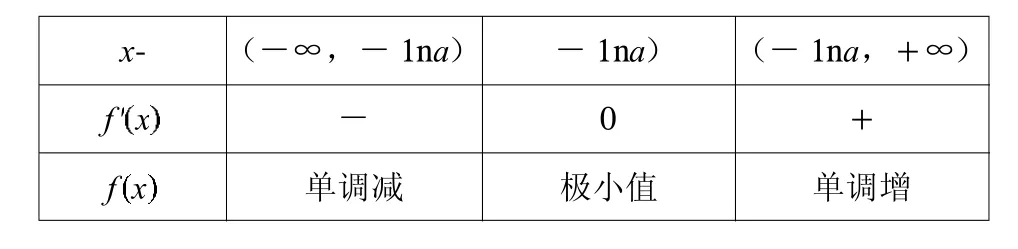
x- （－∞，－1n a） －1n a） （－1n a，+∞）f′x － 0 +f x 單調減 極小值 單調增

當然這里的我們還可以放大。

另外我們如果用動態找點的方法可以在求得0＜a＜1后作如下分析：

當然本題也可以用分離參數法，由這兩道壓軸題的種種解法我們可以看到，壓軸題并非難以突破的，這類題目所考查的核心素養是函數放縮，利用導數確定單調性再放縮。核心素養并非另起爐灶的新搞法，我覺得還得是解決問題所必須具備的核心知識，基本技能技巧，數學運算能力，邏輯推理能力，抽象與想象能力，只有這些能力具備才能夠做到遇到沒教過的問題會用已教過的知識去解決。