一類分?jǐn)?shù)階微分方程m點(diǎn)邊值問題正解的存在性
蔣自國, 董 彪
(1. 阿壩師范學(xué)院 數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院, 四川 汶川 623002; 2. 阿壩師范學(xué)院 數(shù)學(xué)研究所, 四川 汶川 623002)
分?jǐn)?shù)階微分方程在分?jǐn)?shù)物理學(xué)、混沌與湍流、粘彈性力學(xué)與非牛頓流體力學(xué)、高分子材料的解鏈、自動控制理論、化學(xué)物理、隨機(jī)過程、反常擴(kuò)散等自然科學(xué)和工程領(lǐng)域有著非常廣泛的應(yīng)用[1],已經(jīng)成為許多數(shù)學(xué)工作者的研究熱點(diǎn)并做出了許多重要的成果[2-17],其中,分?jǐn)?shù)階微分方程的邊值問題是其重要組成部分.
文獻(xiàn)[13]在Banach空間中研究了如下的分?jǐn)?shù)階微分方程
(1)
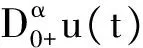
在文獻(xiàn)[8]中,考慮了分?jǐn)?shù)階微分方程邊值問題
(2)
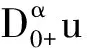
文獻(xiàn)[10]考慮了分?jǐn)?shù)階微分方程邊值問題
(3)
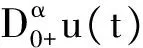
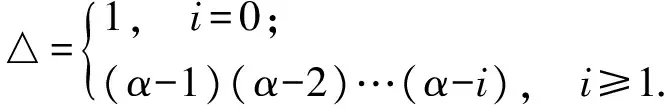
文獻(xiàn)[5]中討論了一類分?jǐn)?shù)階微分方程的邊值問題
(4)
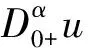
受文獻(xiàn)[5,8,10]的啟發(fā),在本文中,考慮如下分?jǐn)?shù)階微分方程的m點(diǎn)邊值問題
(5)
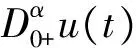
本文始終假設(shè)函數(shù)f:[0,1]×[0,∞)×R滿足如下Carathéodory條件:
1) 對于所有(x,y)∈[0,∞)×R,函數(shù)f(t,x,y)對于變量t在區(qū)間[0,1]上是Lebesgue可測的;
2) 對于幾乎每個(gè)t∈[0,1],函數(shù)f(t,x,y)對于(x,y)在區(qū)域[0,∞)×R是連續(xù)的.
注1當(dāng)h(t)≡1,m=3,邊值問題(5)是文獻(xiàn)[5]中的邊值問題(4).
1 預(yù)備知識和引理
首先給出一些關(guān)于分?jǐn)?shù)階計(jì)算的定義和引理.
定義1[12]函數(shù)y:[0,∞)→R的α>0階Riemann-Liouville積分定義為

定義2[12]函數(shù)y:[0,∞)→R的α>0階Riemann-Liouville微分定義為
其中n為不小于α的最小整數(shù),右邊是在(0,+∞)上逐點(diǎn)定義的.
引理1[3]設(shè)α>0,u∈C(0,1)∩L(0,1),則分?jǐn)?shù)階微分方程
有唯一解
u(t)=C1tα-1+C2tα-2+…+CNtα-N,
Ci∈R,i=1,2,…,N,
其中N是不小于α的最小整數(shù).

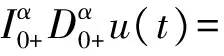
其中N是不小于α的最小整數(shù).
引理3設(shè)y(t)∈C[0,1],α≥2,β≥0,α-β≥1,n-1<α≤n,則m點(diǎn)邊值問題
(6)
有唯一解
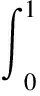
(7)
其中
G(t,s)=
(8)
而G(t,s)是邊值問題(6)的Green函數(shù).
證明由引理2,可將微分方程(6)轉(zhuǎn)化為積分方程
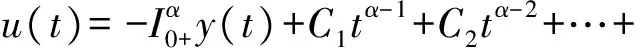
則
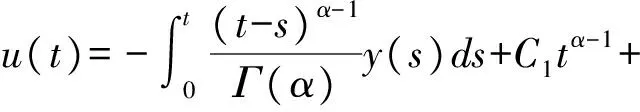
由邊值條件u(0)=u′(0)=…=u(n-2)(0)=0可得C2=C3=…=Cn=0,于是
(9)
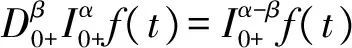
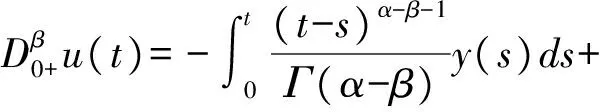
因此
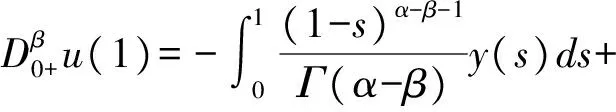

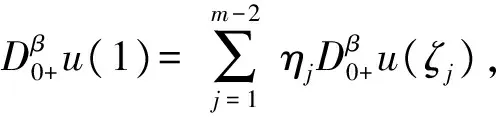
于是得到
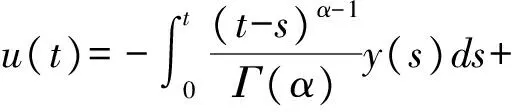
證畢.
引理4引理3中的p(s)在區(qū)間[0,1]上是不減的,且p(s)>0,t∈[0,1].
引理5邊值問題(6)的Green函數(shù)G(t,s)具有以下性質(zhì):
1)G(t,s)在區(qū)域[0,1]×[0,1]上連續(xù);
2)G(t,s)>0,?t,s∈(0,1);
3)tα-1G(1,s)≤G(t,s)≤G(1,s),?t,s∈(0,1).
證明容易證明1)成立,因此,只需證明2)和3)成立.設(shè)
g1(t,s)=p(s)(1-s)α-β-1tα-1-
p(0)(t-s)α-1, 0≤s≤t≤1,
g2(t,s)=p(s)(1-s)α-β-1tα-1,
0≤t≤s≤1.
經(jīng)簡單計(jì)算有
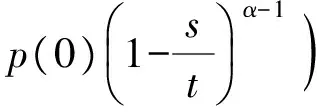
其中
且
故h(t,s)對于變量t在區(qū)間[s,1]是不增的.另一方面
h(1,s)=p(s)(1-s)α-β-1-p(0)(1-s)α-1=
(1-s)α-1(p(s)(1-s)-β-p(0))>0,
因此,對于t∈[s,1],有g(shù)1(t,s)≥tα-1h(1,s)>0.顯然,對于s,t∈(0,1),有g(shù)2(t,s)>0.于是,對于所有s,t∈(0,1),有G(t,s)>0.因此2)成立.
進(jìn)一步有

故Green函數(shù)G(t,s)對于變量t在區(qū)間[0,1]上是不減的,于是
G(t,s)≤G(1,s).
同時(shí),對所有t∈[s,1)有
g1(t,s)≥tα-1h(1,s)=p(0)Γ(α)tα-1G(1,s),
對所有t∈(0,s)有
g2(t,s)=p(s)(1-s)α-β-1tα-1≥
p(0)Γ(α)tα-1G(1,s),
那么
G(t,s)≥tα-1G(1,s).
因此,對所有s,t∈(0,1)有
tα-1G(1,s)≤G(t,s)≤G(1,s).
證畢.
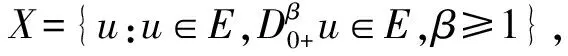
則X是Banach空間[4].在X中定義一個(gè)錐
P={u∈X:u(t)≥0,t∈[0,1]}.
在錐P中定義一個(gè)非負(fù)連續(xù)凹泛函
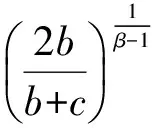

1) 若u∈P(θ,b,d),有{u∈P(θ,b,d):θ(u)>b}≠?且θ(Tu)>b;
2) 若u∈Pa,有‖Tu‖ 3) 若u∈P(θ,b,c)且‖Tu‖>d,有θ(Tu)>b,則T至少有3個(gè)不動點(diǎn)u1、u2和u3,且 ‖u1‖ 為了方便,設(shè) 引理7假設(shè)函數(shù)f:[0,1]×[0,∞)×R→[0,∞)和h:[0,1]→[0,∞)連續(xù),則u∈X是邊值問題(5)的解當(dāng)且僅當(dāng)u∈X是如下積分方程的解 (10) 考慮如下定義的算子T:P→P, (11) 由引理3的證明可知,對任意u∈P有 (12) 引理8由(11)式定義的算子T:P→P是全連續(xù)算子. 證明對于任意u∈P,由(11)式和引理5,可得Tu∈X且Tu(t)≥0,因此,T(P)?P. 1) 由函數(shù)f、h和G的連續(xù)性可知,算子T連續(xù). 2) 下面證明:算子T將錐P中的有界集映為有界集.事實(shí)上,對于任意r>0,對每一個(gè)u∈Ωr={u∈P:‖u‖≤r},令 則由(8)式及引理5有 同時(shí),由(12)式知道 因此 3) 設(shè)Ω?P是有界集,t1,t2∈[0,1],t1 (13) (14) 對任意ε>0,由于函數(shù)tα、tα-1、tα-β-1、tα-1、tα-β在區(qū)間[0,1]上一致連續(xù),因此,存在δ>0,對?t1,t2∈[0,1]:t1 故對任意u∈Ω,t2-t1<δ,由不等式(13)和(14)可得 即T(Ω)等度連續(xù). 由Arzel-Ascoli定理,算子T:P→P全連續(xù).證畢. 成立,如果 則邊值問題(5)存在唯一正解. 證明考慮由(11)式定義的算子T:P→P.將證明T是一個(gè)壓縮映像.事實(shí)上,由(12)式,對任意u,v∈P,有如下估計(jì): 故‖Tu-Tv‖≤η‖u-v‖,其中 由壓縮映像原理,算子T有唯一的不動點(diǎn),即邊值問題(5)有唯一正解.證畢. 定理2若存在一個(gè)非負(fù)實(shí)函數(shù)φ(t)∈L[0,1]∩C[0,1],使得 |f(t,x,y)|≤φ(t)+c1|x|σ1+c2|y|σ2 成立,其中c1,c2∈R為非負(fù)常數(shù),0<σ1,σ2<1,則邊值問題(5)存在正解. 證明設(shè)M={u∈P:‖u‖≤R},其中 只需證明:T:M→M. 對任意u∈M有 故 因此,T:M→M.由引理8知T:M→M全連續(xù).根據(jù)Schauder不動點(diǎn)定理,算子T存在不動點(diǎn)u∈M?P,即邊值問題(5)存在正解.證畢. 定理3若存在常數(shù)0 (H1)f(t,x,y) (H2)f(t,x,y)≤M1c,(t,x,y)∈[0,1]×[0,c]×[-c,c]; (H3)f(t,x,y)≥N1b,(t,x,y)∈[ζ,1]×[b,c]×[-c,-b]∪[b,c], 則邊值問題(5)至少有3個(gè)正解u1、u2和u3,其中 ‖u1‖ 那么 其次,由條件(H1),根據(jù)類似的討論可得,若u∈Pa,則‖Tu‖ 因此{(lán)u∈P(θ,b,c):θ(u)>b}≠?. 最后,若u∈P(θ,b,c),則b≤u(t)≤c且 由條件(H3)及引理5可得 即對任意u∈P(θ,b,c),有θ(Tu)>b. 由引理6,邊值問題5至少有3個(gè)正解:u1、u2和u3,且 ‖u1‖ 證畢. 例1考慮如下的邊值問題 (15) 設(shè)h(t)=t+2,t∈[0,1],則M=3, 取 易證 其中 于是,定理1的所有條件滿足.根據(jù)定理1,邊值問題(15)有唯一正解. 例2考慮邊值問題 (16) 令 h(t)=t+1,t∈[0.1], 容易驗(yàn)證 |f(t,x,y)|≤φ(t)+c1|x|σ1+c2|y|σ2, 例3考慮邊值問題 (17) 和 f(t,x,y)≤0.1125 于是,定理3的所有條件滿足,根據(jù)定理3,邊值問題(17)至少有3個(gè)正解:u1、u2和u3,且 致謝阿壩師范學(xué)院重點(diǎn)科研課題(ASA15-09)對本文給予了資助,謹(jǐn)致謝意. [1] KILBAS A A, SRIVASTAVA H M, TRUJILLO J J. Theory and Applications of Fractional Differential Equations[M]. Amsterdam:Elsevier Science B V,2006. [2] BABAKHANI A, DAFTARDAR-GEJJI V. Existence of positive solutions of nonlinear fractional differential equations[J]. J Math Anal Appl,2003,278(2):434-442. [3] BAI Z B, LYU H S. Positive solutions for boundary value problem of nonlinear fractional differential equation[J]. J Math Anal Appl,2005,311(2):495-505. [4] GUO Y P, GE W G. Positive solutions for three-point boundary value problems with dependence on the first order derivative[J]. J Math Anal Appl,2004,290(1):291-301. [5] 高潔,周瑋. 一類非線性分?jǐn)?shù)階微分方程邊值解的存在性和唯一性[J]. 應(yīng)用數(shù)學(xué)學(xué)報(bào),2014,37(3):470-486. [6] JIANG W H. Eigenvalue interval for multi-point boundary value problems of fractional differential equations[J]. Appl Math Comoput,2013,219(9):4570-4575. [7] 白占兵. 分?jǐn)?shù)階微分方程邊值問題理論及應(yīng)用[M]. 北京:中國科學(xué)技術(shù)出版社,2013. [8] LI C F, LUO X N, ZHOU Y. Existence of positive solutions of the boundary value problem for nonlinear fractional differential equations[J]. Comput Math Appl,2010,59(3):1363-1375. [9] LEGGETT R W, WILLIAMS L R. Multiple positive fixed points of nonlinear operators on ordered Banach space[J]. Indiana Univ Math J,1979,28(4):673-688. [10] 陸心怡,張興秋,王林. 一類分?jǐn)?shù)階微分方程m點(diǎn)邊值問題正解的存在性[J]. 系統(tǒng)科學(xué)與數(shù)學(xué),2014,34(2):218-230. [11] MILLER K S, ROSS B. An Introduction to the Fractional Calculus and Fractional Differential Equations[M]. New York:John-Wiley,1993. [12] PODLUBNY I. Fractional Differential Equations, Mathematics in Science and Engineering[M]. New York:Academic Press,1999. [13] 王永慶,劉立山. Banach 空間中分?jǐn)?shù)階微分方程m點(diǎn)邊值問題的正解[J]. 數(shù)學(xué)物理學(xué)報(bào),2012,A32(1):246-256. [14] YAN R, SUN S R, SUN Y,et al. Boundary value problem for fractional differential equations with nonlocal boundary conditions[J/OL]. Adv Differ Equ,2013(2013):176. https://doi.org/10.1186/1687-1847-2013-176. [15] ZHOU Y. Existence and uniqueness of solutions for a system of fractional differential equations[J]. J Frac Calc Appl Anal,2009,12(2):195-204. [16] 李萍,舒級,張佳,等. 一個(gè)具有相互作用非線性項(xiàng)的分?jǐn)?shù)階微分方程組的爆破解[J]. 四川師范大學(xué)學(xué)報(bào)(自然科學(xué)版),2016,39(1):15-19. [17] 古傳運(yùn),鄭鳳霞,鐘守銘. 一類非線性分?jǐn)?shù)階微分方程邊值問題正解的存在唯一性[J]. 四川師范大學(xué)學(xué)報(bào)(自然科學(xué)版),2015,38(1):72-76.2 主要結(jié)果及證明
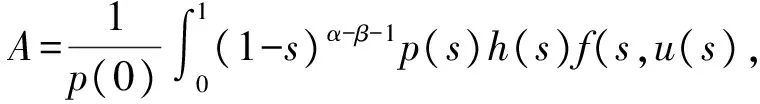
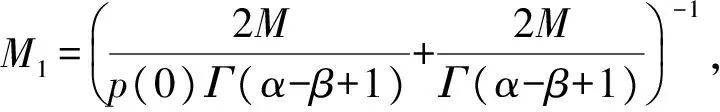

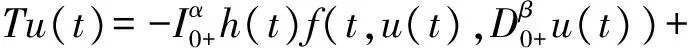


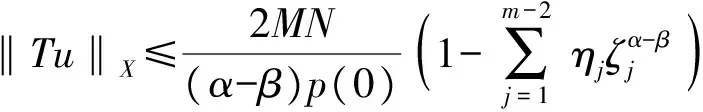
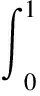
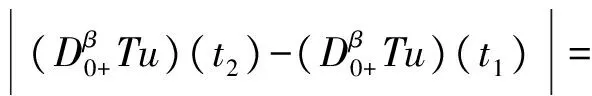
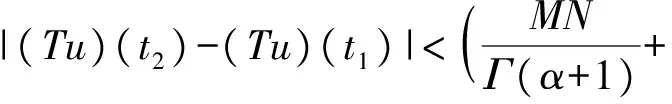
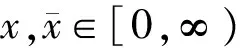


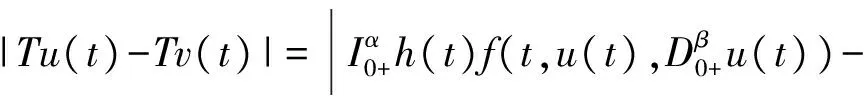
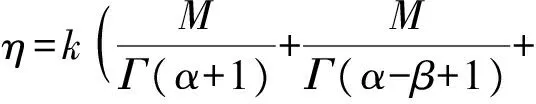


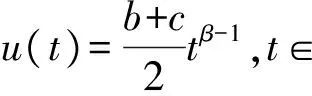
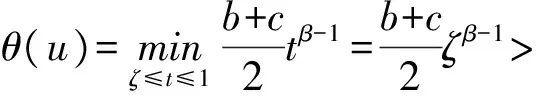
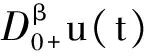
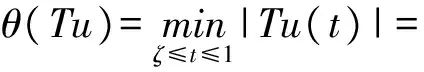
3 例子



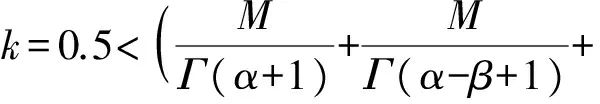


0<σ1,σ2<1,
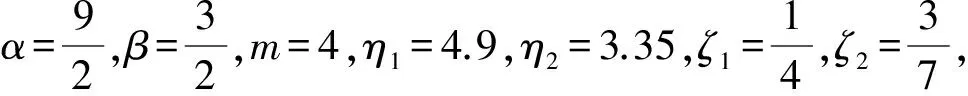

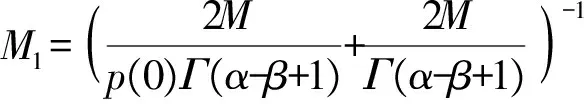
f(t,x,y)≤57.1≤M1c=65.464 2,
(t,x,y)∈[0,1]×[0,c]×[-c,c];
f(t,x,y)≥24.227 5≥N1b=23.848 8,
(t,x,y)∈[ζ,1]×[b,c]×[-c,-b]∪[b,c].

