半群OIn(k,m)的秩
易 林, 游泰杰, 趙 平
(貴州師范大學 數學科學學院, 貴州 貴陽 550001)
設[n]={1,2,…,n},并賦予自然序,Tn、Pn、In和Sn分別是[n]上的全變換半群、部分變換半群、對稱逆半群和對稱群.設α∈Pn,若對任意x,y∈dom(α),x≤y?xα≤yα,則稱α是保序的.設On為Tn中所有保序變換之集(不含[n]上的恒等變換),則On是Tn的子半群,稱On為[n]上的保序變換半群;設POn為Pn中所有保序變換之集(不含[n]上的恒等變換),則POn是Pn的子半群,稱POn為[n]上的部分保序變換半群;設OIn為嚴格對稱逆半群InSn中的所有保序變換之集,則OIn是InSn的逆子半群,稱OIn為保序嚴格部分一一變換半群.對任意1≤k,m≤n,令
On(k)={α∈On:(?x∈[n])x≤k?xα≤k},
POn(k)={α∈POn:(?x∈dom(α))x≤k?xα≤k},
POn(k,m)={α∈POn:(?x,y∈dom(α))x≤
k?xα≤k,y≥m?yα≥m},
則On(k)、POn(k)和POn(k,m)均是POn的子半群.
通常,一個半群S的秩定義為
rank S=min{|A|:A?S,〈A〉=S}.
變換半群秩的相關研究一直以來都是半群理論研究中的熱點之一[1-9].特別地,文獻[1]證明了On(=On(n))的秩是n和POn(=POn(n))的秩是2n-1;文獻[2]得到了半群On(k)秩是n;文獻[3]得到了半群POn(k)秩為2n-1;文獻[4]得到了半群POn(k,k+1)秩為2n-2和半群POn(k,m)(m≠k+1)秩為2n-1;文獻[5]研究了半群OIn的表示與秩,得到了半群OIn的秩是n.本文將考慮半群
OIn(k,m)={α∈OIn:(?x,y∈dom(α))x≤
k?xα≤k,y≥m?yα≥m}
的秩,其中1≤k≤n-1,2≤m≤n,證明了半群OIn(k,k+1)的秩為n,且半群OIn(k,m)(m≠k+1)的秩為n+2.注意到,當k=n,m=1時,OIn(n,1)=OIn.因此,本文是對文獻[5]結果的推廣.
設U是半群S的任意子集,通常用E(U)表示U中所有冪等元構成的集合.本文未定義的術語及記法參見文獻[10-12].
1 預備知識
為了敘述方便,在OIn(k,m)上引入下面二元關系:對任意α,β∈OIn(k,m),定義:
αR◇β?ker(α)=ker(β),
αL◇β?im(α)=im(β),
αJ◇β?|im(α)|=|im(β)|,
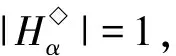
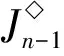
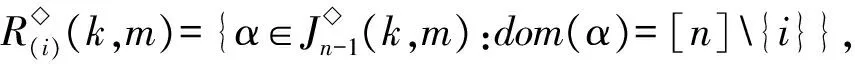
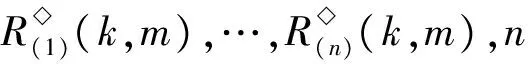
2 主要結果及證明
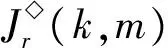
證明任意取

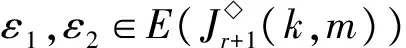
情形2若α為非恒等變換,則以下分5種子情形討論:
1)m≤br≤k.由b1 2)m≤k (i) |{1,2,…,m-1}{a1,…,as-1}|=0且|{k+1,k+2,…,n}{ai,ai+1,…,ar}|=0.注意到 令 (ii) |{k+1,k+2,…,n}{ai,ai+1,…,ar}|=1.由r≤n-2可得存在2個不同元素x,y∈[n],使得x∈{1,2,…,k}{a1,…,ai-1},y∈{k+1,k+2,…,n}{bi,…,br}.假設au (iii) |{k+1,k+2,…,n}{ai,ai+1,…,ar}|≥2.令 3)k≤m 4)k≤br 5)br 令 G(k,m)= 引理2設1≤k≤n-1,且2≤m≤n,則 情形1k+1=m.以下分4種子情形討論: 2) 若j≤i≤m-1,易驗證 4) 若m 情形2k+1 2) 若j≤i≤k≤n-1,易驗證 3) 若k+1≤j≤i≤m-1,易驗證 4) 若k+1≤j≤m-1≤i≤n-1,易驗證 6) 若m≤j 情形3m≤k.以下分6種子情形討論: 2) 若1 3) 若1≤j≤m-1≤i 4) 若m≤j≤i≤k,易驗證 6) 若m≤j≤i 引理3設α,β∈OIn(k,m),若 (α,β)∈J◇, (α,αβ)∈J◇, 則 (αβ,β)∈L◇, (α,αβ)∈R◇. 證明對α,β∈OIn(k,m),若 (α,β)∈J◇, (α,αβ)∈J◇, 則 |im(α)|=|im(β)|=|im(αβ)|. 再由im(αβ)?im(β),ker(α)?ker(αβ)(由|im(α)|=|im(αβ)|易得dom(α)?dom(β),從而ker(α?ker(αβ))可得im(αβ)=im(β),ker(α)=ker(αβ)).因此 (αβ,β)∈L◇, (α,αβ)∈R◇. 證明假設 且ci=bi(i∈{1,2,…,n-1}),從而可得 對任意0≤r≤n-1,記 OIn,r(k,m)={α∈OIn(k,m):|im(α)|≤r}, 則OIn,r(k,m)是半群OIn(k,m)的理想.顯然OIn,n-1(k,m)=OIn(k,m). 為方便起見,引入符號 其中∧,Σ是[n]的任意2個非空子集. 引理5設1≤k≤n-1,且2≤m≤n,S是OIn(k,m)任意非空子集,則: (i) 若m=k+1,則|S|≥n; (ii) 若m≠k+1,則|S|≥n+2. (ii) 若m≠k+1,則分以下2種情形討論: 情形12≤k+1 其中 P1={1,2,…,k}, 另一方面,將證明|S∩H◇(P1,P2)|≥1且|S∩H◇(P3,P2)|≥1.對任意α,β∈H◇(Pi,Pi)(i∈{1,2,3}),由引理3可得αR◇αβL◇β或αβ∈OIn,n-2(k,m).注意到,對任意α∈H◇(P1,P1),β∈H◇(P2,P2),則 再由引理4可得αβ即 αβH◇(P1,P2), |S∩H◇(P1,P2)|≥1. 同理可證,對任意 α∈H◇(P3,P3),β∈H◇(P2,P2), 則 αβH◇(P3,P2), |S∩H◇(P3,P2)|≥1. 情形22≤m≤k≤n.注意到 其中 P1={1,2,…,m-1}, 證明過程類似情形1. 綜合情形1和2可得:|S|≥n+2. 定理1設1≤k≤n-1,且2≤m≤n,則 證明由推論1及引理2可得 OIn(k,m)?〈G(k,m)〉, 從而 rankOIn(k,m)≤|G(k,m)|. 易驗證 因此 [1]GOMESGMS,HOWIEJM.Ontheranksofcertainfinitesemigroupsoforder-preservingtransformation[J].SemigroupForum,1992,45(1):272-282. [2] 張傳軍,趙平. 半群On(k)的秩[J]. 數學的實踐與認識,2014,44(9):243-247. [3] 李先崇,趙平. 半群POn(k)的冪等元秩[J]. 西南大學學報(自然科學版),2013,38(10):9-12. [4] 張傳軍,朱華偉,肖宏治. 半群POn(k,m)的秩[J]. 西南大學學報(自然科學版),2016,41(6):6-11. [5]FERNANDESVH.Themonoidofallinjectiveorderpreservingpartialtransformationsonafinitechain[J].SemigroupForum,2001,62(2):178-204. [6] 徐波,馮榮權,高榮海. 一類變換半群的秩[J]. 數學的實踐與認識,2010,40(10):222-224. [7] 高榮海,徐波. 降序且保序有限部分變換半群的冪等元秩[J]. 西南大學學報(自然科學版),2008,30(8):9-12. [8] 趙平,游泰杰,徐波. 半群CPOn的秩[J]. 西南大學學報(自然科學版),2011,33(6):106-110. [9] 高榮海,徐波. 核具有連續橫截面的保序變換半群的秩[J]. 西南大學學報(自然科學版),2013,38(4):19-24. [10]HOWIEJM.FundamentalsofSemigroupTheory[M].NewYork:OxfordUniversityPress,1995. [11]CLIFFORDH,PRESTONGB.Thealgebraictheoryofsemigroups[C]//AmMathSoc.NewYork:Providence,1961. [12]GANYOSHKINO,MAZORCHOKV.ClassicalFiniteTransformationSmigroup[M].London:Springer-Verlag,2009. [13] 吳金艷,趙平,游泰杰. 半群OIn的偏度秩[J]. 西南大學學報(自然科學版),2015,37(10):67-71.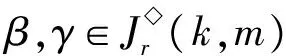
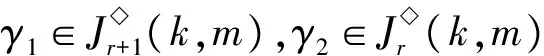
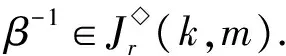
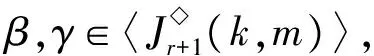
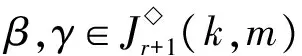
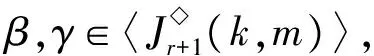
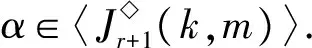
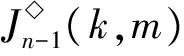
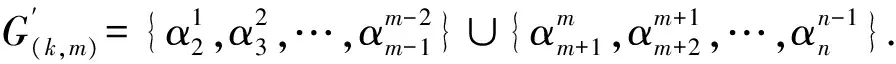
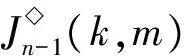
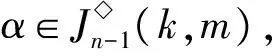
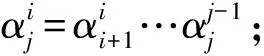
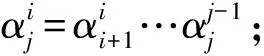
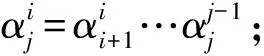

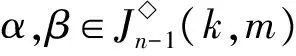
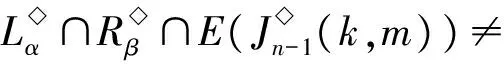
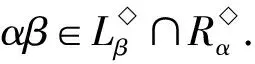
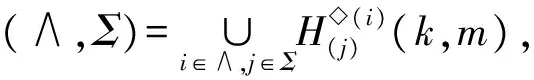
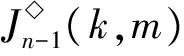
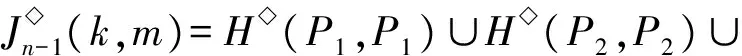
P2={k+1,k+2,…,m-1},
P3=[n](P1∪P2).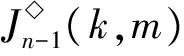
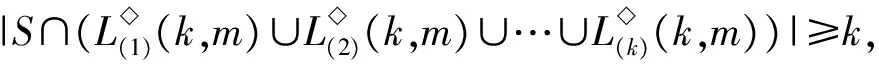
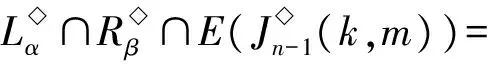
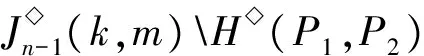
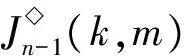
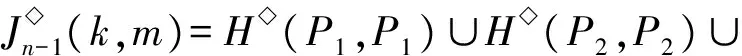
P2={m,m+1,…,k},
P3=[n](P1∪P2).

