形如2α-1p1p2p3的near-perfect數
馮 遷, 廖群英
(四川師范大學 數學與軟件科學學院, 四川 成都 610066)
2000多年前歐幾里得提出perfect(完美)數的概念,稱滿足σ(n)=2n的正整數n為完美數,其中σ(n)表示n的所有正因子之和,并構造出了所有的偶完美數;但是歐幾里得不能給予完整的證明,最終歐拉完成了這個任務,其生成方式和梅森素數有直接關系,即n為偶完美數當且僅當n=2k-1(2k-1),其中k、2k-1均是素數[1-3].2000多年過去了,梅森素數的無窮性、奇完美數的存在性等問題仍然難以解決[4-9].于是與此相關的概念誕生,比如本文考慮的near-perfect數.
定義1[3]若正整數n,使得等式σ(n)=2n+d成立,其中d是n的真因子,則稱n為near-perfect數,并稱d為n的冗余因子.(注意到,如果n是near-perfect數,則冗余因子d是唯一的.)
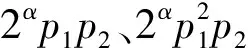
對于形如n=2α-1p1p2p3的n-p數,其中α∈Z,α≥2,p1、p2、p3是不同的奇素數且p1 (2α-1)(p1+1)(p2+1)(p3+1)= (1) 對以上等式奇偶分析易得2|d.于是 d∈{2β,2βp1,2βp2,2βp3,2βp1p2,2βp1p3, 在(1)式中令p1+1=k,即得 (2α-1)k(p2+1)(p3+1)=2αp1p2p3+d. 若p3|d,則由p1 均與p2是正數矛盾,故只需考慮5種情況:d=2β、2βp1、2βp2、2βp1p2、2βp1p2p3. 本文給出冗余因子d=2β、2βp1或2βp2時,n的一種生成方式;進而在條件p1?(p2+1)下,得到d=2α-1p1p2時,n的全部取值;最后對d=2βp1p2p3的情形得到一些基本性質. 定理1設α、β、γ均為正整數,p1=2α+2β-γ-1為奇素數.令 u=22α+γ-β+2α-2α+γ-β. 若存在正整數x,y>1,滿足 u(u-1)-2γ=xy, 且p2=x+u-1和p3=y+u-1均為奇素數,則 n=2α-1p1p2p3 是以d=2β為冗余因子的n-p數,其中2≤γ≤β-1≤α-2. 定理2設α、β、γ均為正整數,p1=2α+2α-γ-1為奇素數.若存在分解 p1(2α+γ-βp1-2α-β-1)=2α-β-γxy, 使得 p2=x+2α+γ+2α-2γ-1, p3=y+2α+γ+2α-2γ-1 均為奇素數,則n=2α-1p1p2p3是以d=2βp1為冗余因子的n-p數,且1≤γ≤β≤α-1. 定理3設α、β均為正整數,p1、p2、p3為不同的奇素數,p1 其中,1≤β≤α-2,t∈Z. 命題1設α、β、γ均為正整數,p1、p2、p3為不同的奇素數,p1 p1?(p2+1), 則不存在以d=2βp1p2p3為冗余因子的形如n=2α-1p1p2p3的n-p數,其中α>β>γ≥1. 命題2設p1、p2、p3為不同的奇素數,p1 定理1的證明由p1=2α+2β-γ-1為奇素數,且 u=22α+γ-β+2α-2α+γ-β, p2=x+u-1,p3=y+u-1, xy=u(u-1)-2γ, 可得 (p2+1-u)(p3+1-u)=xy=u(u-1)-2γ. (2α-1)(p1+1)(p2+1)(p3+1)-2αp1p2l3=2β. 從而由定義1可得定理1. 定理2的證明因為p1=2α+2α-γ-1,不妨設u=2γp1,則奇素數p2=x+u-1,p3=y+u-1.從而由σ(n)的定義可知 故由定義1可知定理2成立. 定理3的證明必要性 即若n=2α-1p1p2p3是以d=2α-1p1p2為冗余因子的n-p數,其中 p1?(p2+1), 則由(1)式可知 (p1+p2+1)(p3+1)(2α-1)= (2) 注意到p1 1)p1|(p3+1)且p2|(2α-1); 2)p1|(2α-1)且p2|(p3+1); 3)p1p2|(2α-1); 4)p1p2|(p3+1). 通過(2)式容易排除形1)~3),故只需考慮情形4).不妨設p1p2u=p3+1,代入(2)式得 u[(p1+p2+1)(2α-1)-p1p2]= -2α-1?u=2β, 1≤β≤α-1. 注意到p1?(p2+1),此時情形4)等價于如下方程組 (3) 至此,將其轉化為文獻[10]中的定理2.1中的(3)的情形,于是可得其所有解為 充分性 根據n-p數的定義容易驗證(1)式成立,故得證. 命題1的證明反證法 設n=2α-1p1p2p3是以d=2βp1p2p3為冗余因子的n-p數,則由(1)式可知 因奇質數p1=2α+2β+2γ-1,故上式等價于 2γp1(p2+p3+1)=(p2+1)(p3+1). (4) 在(4)式中,由整除性關系有:p1|(p2+1)或p1|(p3+1). 由命題假設p1?(p2+1),只需考慮p1|(p3+1): 若p1|(p3+1),不妨設p1l1=p3+1,將其代入(4)式得 l1(p1(2α-γ+2β-γ)-1)= (5) 在(5)式中由整除性有p2|l1或 p2|(p1(2α-γ+2β-γ)-1). 當p2|(p1(2α-γ+2β-γ)-1)時,不妨設 p2l2=p1(2α-γ+2β-γ)-1, 將其代入(5)式得 l1l2=l1-2α-2β-γ, 不可能,排除;當p2|l1,不妨設p2l3=l1,結合p1l1=p3+1,有p1p2l3=p3+1.將其代入(1)式容易得到p3|2α-1,這與 p3>p1=2α+2β+2γ-1>2α-1, 矛盾. 綜上可知命題1成立. 命題2的證明已知n=2α-1p1p2p3是以d=2β為冗余因子的n-p數,若 為奇素數,容易驗證等式 σ(n′)=2n′+2βpi,i=1,2 注1一些比較有趣的問題: 1) 以d=2β為冗余因子的形如 n=2α-1p1p2p3 的n-p數是否無窮多? 2) 對每個α≥2,都有形如n=2αp1p2p3的n-p數? 3) 在偶n-p數集合中,當2?d時,d必是梅森素數嗎? 4) 確定第m個n-p數的漸進形式; 5) 確定所有奇n-p數的性質或判別準則. 注2利用計算機搜索到了滿足定理1~3以及命題2條件的n-p數分別如下: 1)n=5 020 330 978 238 336, n=338 107 574 312 576, n=606 612 165 182 277 661 184; 2)n=22 342 536 833 728, n=1 883 115 542 848, n=606 612 165 182 277 661 184; 3)n=2 510 165 914 244 992, n=2 510 165 914 244 992, n=388 660 513 622 544 896; 4)n=1 845 991 216,n=6 800 228 816. [1] VOIJHT J. Perfect Numbers:An Elementary Introduction[M]. Berkley:University of California,1998. [2] 華羅庚. 數論導引[M]. 北京:商務印書館,1967. [3] POLLACK P, SHEVELEV V. On perfect and near-perfect numbers[J]. Number Theory,2012,132(12):3037-3046. [4] POMERANCE C. Multiply perfect numbers, Mersenne primes, and effective computability[J]. Math Ann,1977,226(3):195-206. [5] BATEMAN P T, SELFRIDGE J L, WAGSTAFF S S. The editor’s corner:the new mersenne conjecture[J]. Am Math,1989,96(2):125-128. [6] BROWN H D R. Odd perfect numbers[C]//Mathematical Proceedings of the Cambridge Philosophical Society,1994,115(2):191-196. [7] BRENT R P, COHEN G L, RELE H J. Improved techniques for lower bounds for odd perfect numbers[J]. Math Comput,1991,57(196):857-868. [8]WEISSTEIN E W. Odd perfect number[C/OL]//Wolfram Math World:A Wolfram Web Resource. http://mathworld.wolfram.com/OddPerfectNumber.html,2004. [9] FLETCHER S, NIELSEN P, OCHEM P. Sieve methods for odd perfect numbers[J]. Math Comput,2012,81(279):1753-1776. [10] LI Y B, LIAO Q Y. A class of new near-perfect numbers[J]. Korean Math Soc,2015,52(4):751-763. [11] JERRARD R P, TEMPERLEY N. Almost perfect numbers[J]. Math Mag,1973,46(2):84-87. [12] HARDY G H, WRIGHT E M. An Introduction to the Theory of Numbers[M]. New York:Oxford University Press,1979. [13] HORNFECK B, WIRSING E. über die H?ufigkeit vollkommener Zahlen[J]. Math Ann,1957,133(5):431-438. [14] WIRSING E. Bemerkung zu der Arbeit über vollkommene Zahlen in Math. Ann. Bd. 133, S. 431-438 (1957)[J]. Math Ann,1959,137(4):316-318. [15] TANG M, MA X Y, FENG M. On near-perfect numbers[J]. Colloqu Math,2016,144(2):157-188.
2αp1p2p3+d.
2βp2p3,2βp1p2p3}, 1≤β≤α-1.
1 主要結果
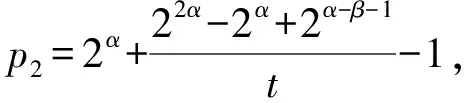
2 主要結果的證明
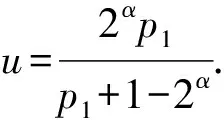
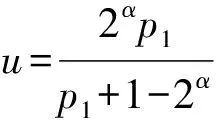
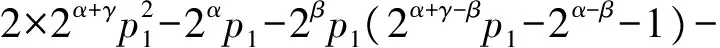
(p3-2α-1+1)p1p2.
p2(l1-2α-γ-2β-γ).

