基于ESO的BTT飛行器多變量解耦控制方法研究

杜立夫，張 瑞，趙志芳，閔 勇

(北京航天自動控制研究所，北京 100854)

0 引言

傾斜轉彎(BTT)飛行器采用高升阻比的面對稱氣動外形,能產生高升力、大過載，在機動性、穩定性、升阻比特性和沖壓發動機進氣口設計的兼容性等方面，相比側滑轉彎(STT)飛行器有顯著的性能優勢[1-2], 受到國內外相關研制單位的高度重視,且發展迅速。

BTT飛行器的機動過程是：利用滾動通道快速將飛行器最大升力面滾轉到所要求的機動方向;利用俯仰通道控制飛行器，使其在最大升力面內產生相應的攻角,獲取需要的過載；利用偏航通道嚴格控制側滑角，協調控制俯仰通道和滾轉通道的運動，使側向過載和側滑角近似為零。故BTT飛行器的滾動角速率和滾動角度比STT飛行器大很多。另外，側向風引起的斜吹力矩和不確定性因素會產生相應的瞬間側滑角，致使飛行器俯仰通道、偏航通道和滾轉通道之間嚴重耦合,從而使飛行器系統成為一個強耦合、復雜的多變量系統[3]。傳統的三通道獨立控制設計已不再適用于BTT飛行器,控制系統設計時須考慮運動學耦合、慣性耦合、氣動耦合和控制作用耦合等多自由度耦合問題。

隨著控制理論與應用的不斷發展，越來越多的先進控制技術(如魯棒控制、滑模控制、非線性動態逆控制等)被應用到BTT飛行器的解耦控制中。文獻[4]中建立BTT導彈線性變參數模型,將耦合視為擾動，運用最小靈敏度特征值配置的魯棒方法完成控制器設計，但控制方法較為繁瑣，不易實現；文獻[5]中運用變結構控制方法完成BTT導彈解耦控制，展示出良好的控制效果，但控制量具有抖動，需要進一步解決；文獻[6]中運用非線性動態逆設計解耦控制器，解決了BTT飛行器的耦合問題和快速跟蹤問題，動態逆方法是一種有效的非線性控制方法，但非線性動態逆在設計過程中對模型不確定性較敏感，需要增加系統的魯棒性。

自中科院韓京清研究員提出自抗擾控制技術[7](ADRC)以來，該技術在理論和工程上取得了巨大的成果[8-9]。這得益于自抗擾控制技術中核心部分——擴張狀態觀測器(ESO)的引入，它可將系統的不確定性、未建模動態和外部擾動等視為“總和擾動”，并將其擴張成系統變量，然后設計狀態觀測器以實現對擾動的估計, 將其輸出補償到控制系統中，從而提高系統的性能。ESO不需要精確的模型信息，結構簡單，易于實現，故其通用性較高，并在理論和工程實踐中得到不斷的發展和應用[10-12]。

通常，解決多變量耦合控制方法有兩種。一種是將耦合視為擾動，通過設計增加控制器的魯棒性來抑制耦合擾動的影響，增加了控制器的復雜程度，增大了控制器的負擔，耦合大時解耦效果會受到一定的影響；另一種是建立耦合量的先驗模型，通過補償方法完成解耦控制[13]，模型的精確度會影響解耦控制的效果。為此，本文提出一種基于ESO的BTT飛行器多變量解耦控制方法，用反饋機制建立能觀測耦合擾動作用的擴張狀態觀測器，該擴張狀態觀測器并不依賴生成耦合擾動的具體數學模型，也無須直接測量其作用，利用已知三通道獨立設計控制器模型即可完成擴張狀態的觀測，不需要其他模型量即可實現對耦合擾動的估計與補償，進一步設計獨立三通極點配置的閉環反饋控制器，完成多變量的解耦控制，是一種通用、實用、便于工程實現的方法。

1 數學模型的建立

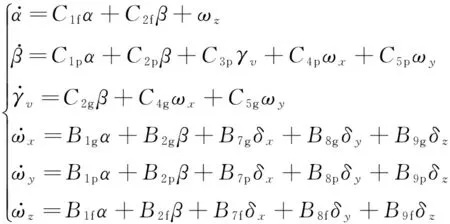
(1)

式中：α為攻角；β為側滑角；γv為速度傾側角；δx為滾動舵偏角；ωz為俯仰角速度；ωy為偏航角速度；ωx為滾轉動角速度；δy為偏航舵偏角；δz為俯仰舵偏角；C、B為動力學方程系數，下角標f,p,g分別表示俯仰通道、偏航通道和滾轉通道。顯然，BTT飛行器數學模型是一個多變量耦合系統。

2 基于ESO的多變量解耦控制

將式(1)中的全部耦合項去掉，并將耦合項視為擾動，利用已知獨立三通道模型設計ESO，觀測耦合擾動，通過補償方法進行解耦，進一步設計穩定的、獨立三通極點配置的閉環反饋控制器，完成基于ESO的多變量解耦控制。

2.1 ESO的設計介紹

ESO是自抗擾控制技術[7]的重要組成部分，它可較為精確地估計出系統當前的不確定性，將這種不確定性補償到控制系統中，從而增加系統的抗干擾能力。下面將闡述ESO的設計過程。

以2階系統為例，多變量線性系統模型可表示為

(2)

式中：F(x1,x2)和G(x1,x2)為系統關于x1和x2的非線性函數向量模型，x1∈Rn、x2∈Rn均為系統狀態向量，u∈Rm為控制輸入向量。假設系統的一部分模型已知，把這個模型稱作名義模型，則式(2)可改寫為

(3)

式中：F0(x1,x2)、G0(x1,x2)為名義模型，而Fu(x1,x2)、Gu(x1,x2)為未知模型。則需要擴張的狀態向量可表示為

d=Fu(x1,x2)+Gu(x1,x2)u

(4)

根據式(3)和式(4)，ESO設計式為

(5)

式中：向量z1為對系統向量x1的估計；向量z2為對系統向量x2的估計；z3為對不確定性向量d的估計；β01、β02、β03為ESO設計參數，使其均大于零即可保證擴張狀態觀測器穩定收斂[7]；f(e,κ,δ)為原點附近線性、連續的冪次函數，即

(6)

式中：e為ESO的偏差輸入；δ為線性區間長度，一般取較小的數；κ為冪次函數的冪，一般取0.5。

由式(5)可知，把名義模型放入擴張狀態觀測器中，可得

(7)

此時被擴張的狀態變量d的估計值z3(t)估計的就是作用于系統的不確定性部分，即ESO實時估計擾動功能，將這種擾動估計加以補償實質就是抗干擾。

擴張狀態觀測是一個動態過程，觀測器的結構示意圖如圖1所示。

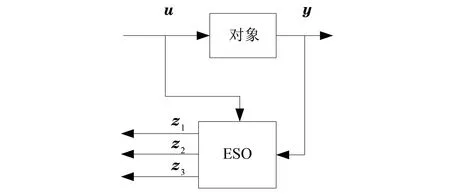
圖1 ESO結構示意圖Fig.1 ESO structural schematic diagram

2.2 ESO的多變量解耦控制器設計

將BTT飛行器全量模型式(1)，去掉所有耦合項作為三通道獨立設計的名義模型，其狀態方程可表示為

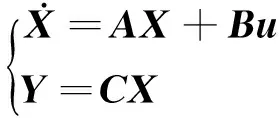
(8)

式中：狀態變量X=[x1x2x3x4x5x6]T=[αβγvωzωyωx]T；控制變量u=[δxδyδz]T；輸出變量Y=[αβγv]T。狀態矩陣

(9)

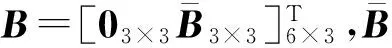
(10)

輸出矩陣C=[I3×303×3]。

把式(8)模型作為名義模型，進行ESO設計，完成狀態和擾動估計，根據2.1節ESO設計介紹，ESO設計如下

(11)

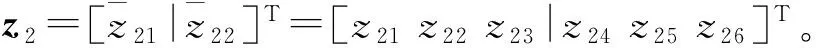
(12)

式中：u0為閉環反饋控制律。

2.3 ESO的極點配置閉環反饋控制器設計

系統的性能和穩定性主要是由系統的特征根決定，即系統的極點。極點配置的狀態反饋控制方法可使系統獲得更優異的性能，下文運用極點配置的方法設計獨立三通道控制器，完成閉環反饋控制。

由式(8)設計閉環狀態反饋控制律，表達式為

u0=KX

(13)

式中：K為狀態反饋控制參數向量。

將控制律具體形式展開，即

(14)

式中：kf1,kf2為俯仰通道反饋控制參數；kp1,kp2為偏航通道反饋控制參數；kg1,kg2為滾轉通道反饋控制參數。

對三通道獨立系統進行極點配置，俯仰通道、偏航通道和滾轉通道的期望極點分別是-3±4j、-4±6j和-2±6j，由控制理論可知，系統中的特征根均分布在左半平面內，故可保證系統穩定[14]。通過MATLAB中極點配置函數K=place(A,B,p),即可得到三通道反饋控制參數向量K。

初始偏差Δα0=1°，Δβ0=1°，Δγv0=1°時的獨立三通道系統的零輸入響應，如圖2所示,可以看出，獨立三通道系統穩定，且參數很快收斂。圖3為ESO的BTT飛行器解耦控制系統框圖。

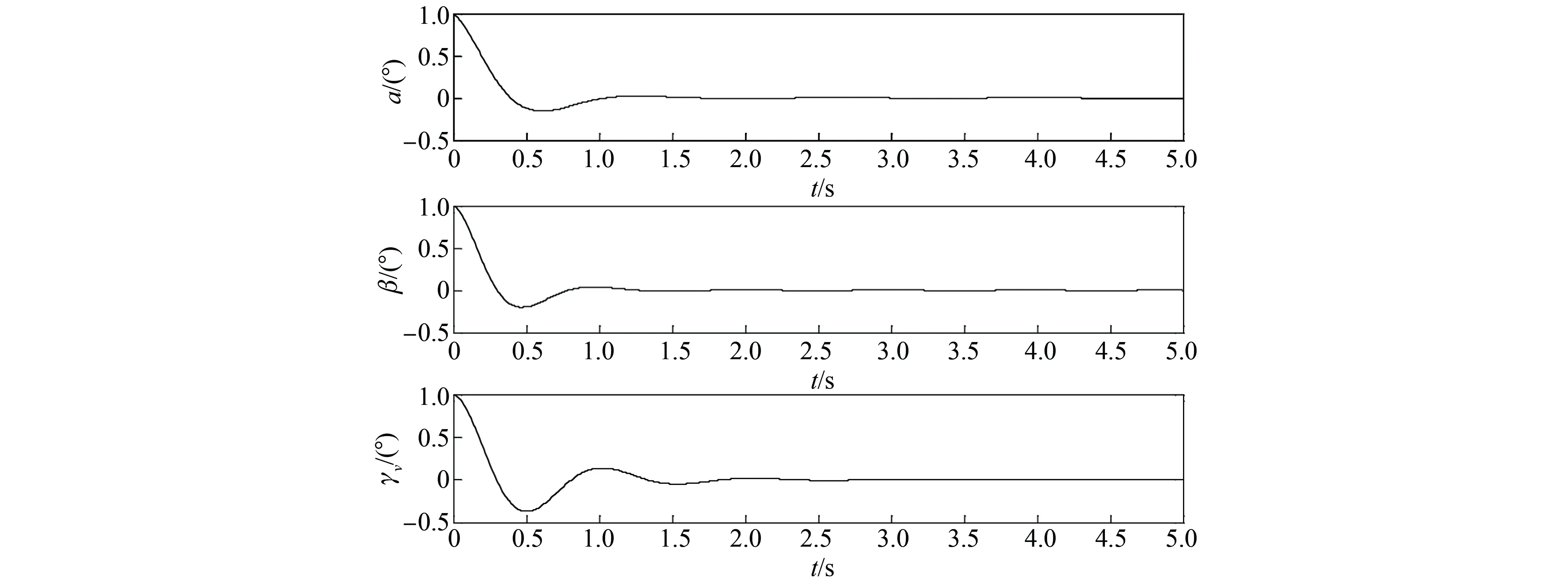
圖2 獨立三通道狀態的零輸入響應曲線Fig.2 Zero input response curve of the independent three-channel state

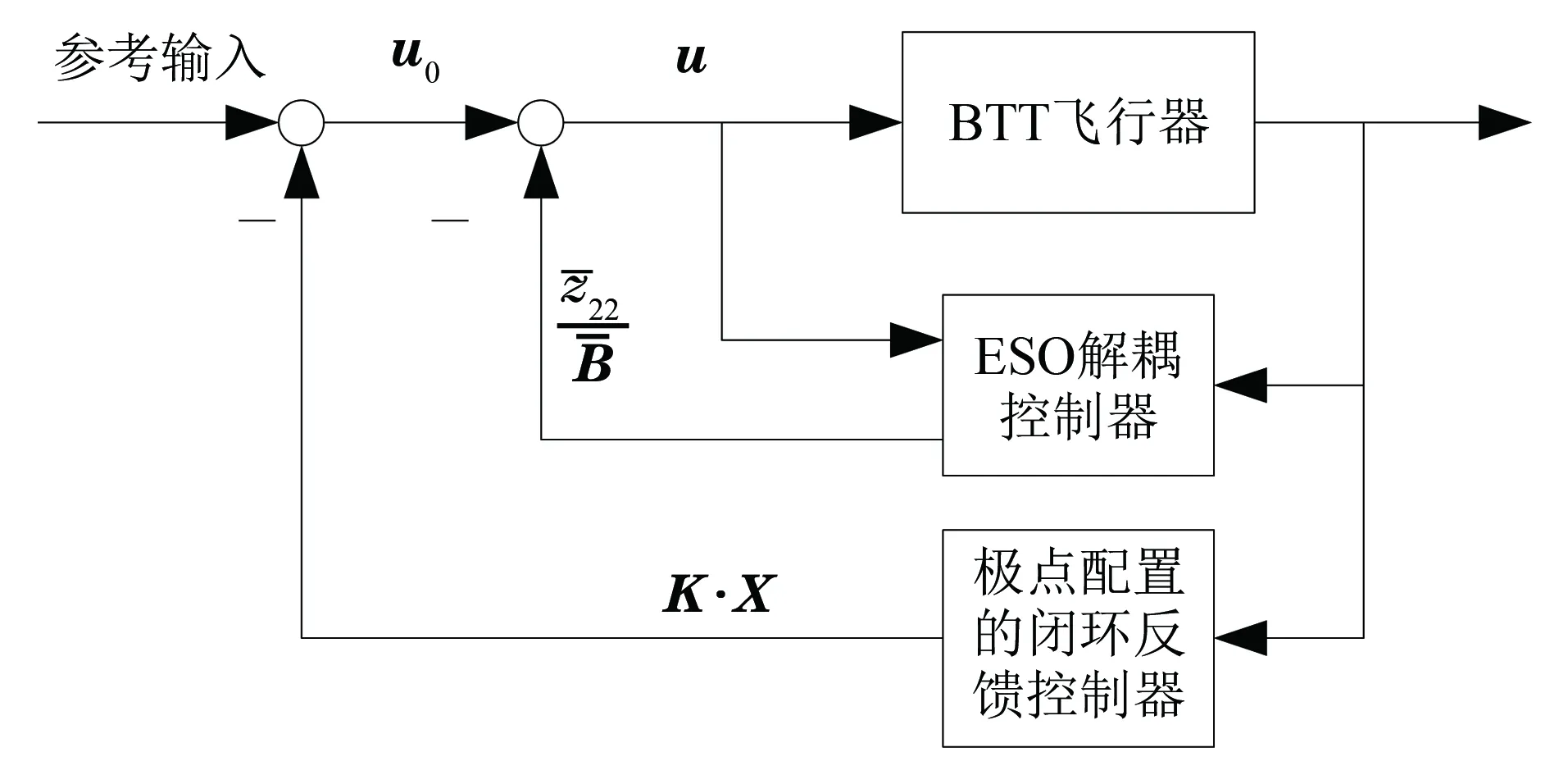
圖3 基于ESO的BTT飛行器解耦控制系統框圖Fig.3 Block diagram of decoupling control system for BTT aircraft based on ESO

3 仿真校驗

基于MATLAB仿真分析BTT飛行器多變量耦合控制器，驗證系統的解耦特性和控制系統性能。

3.1 仿真參數

選取BTT飛行器空域中的某特征點，其中飛行器質量、特征面積、特征長度、轉動慣量參數均為已知，則飛行器的模型參數均為已知參數。

根據BTT飛行器控制要求，攻角初值取α0=0°,控制目標αcx=5°；側滑角初值取β0=1°,控制目標βcx=0°；傾側角初值取γv0=0°,控制目標γvcx=5°。

ESO參數設計如下

(15)

極點配置的三通道反饋控制參數如下

(16)

3.2 仿真結果

仿真周期為10 s，分別對極點配置方法設計的三通道獨立控制器和ESO解耦控制器進行仿真對比，指令跟蹤結果如圖4～6所示。ESO對三通道耦合干擾的估計曲線如圖7～9所示。

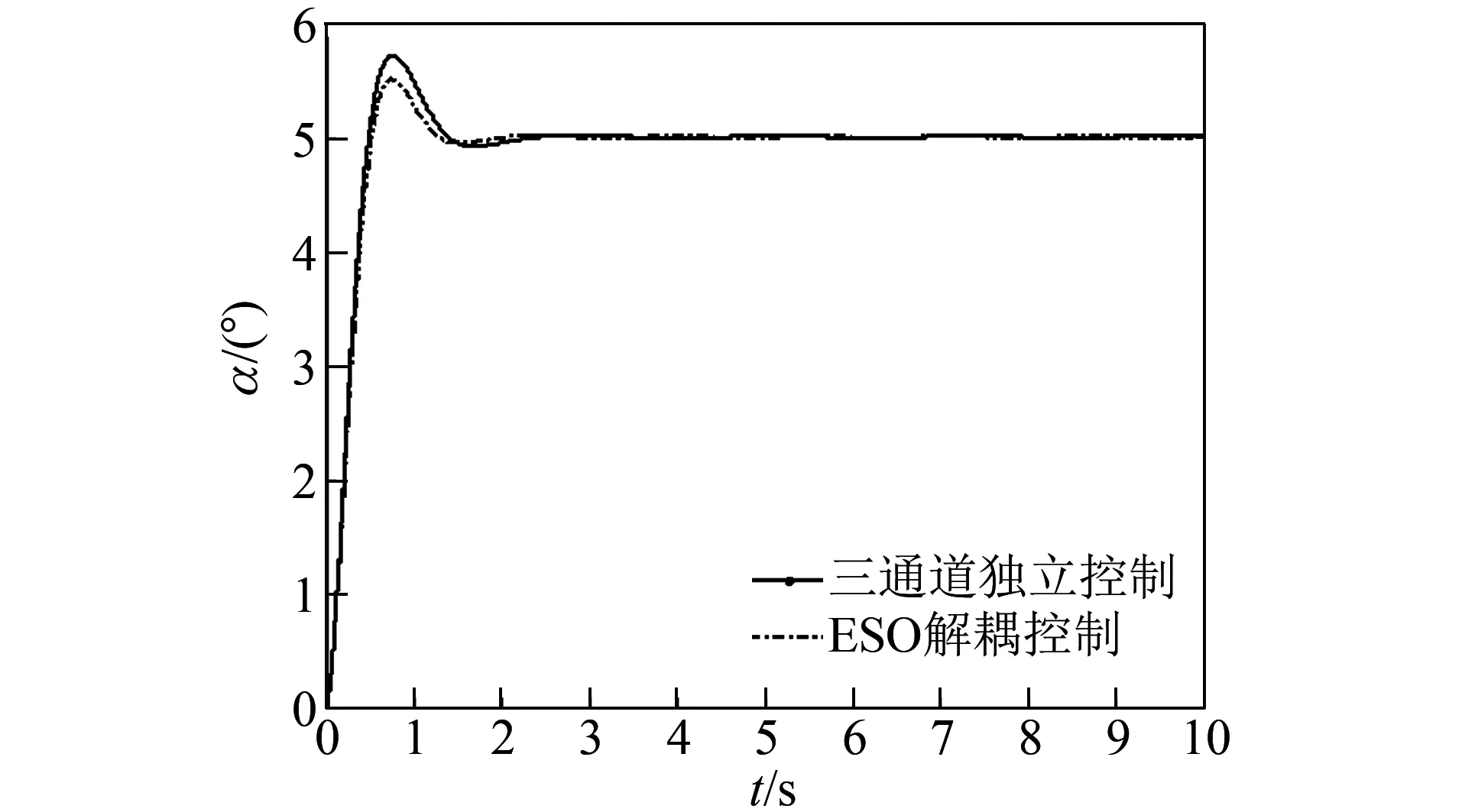
圖4 攻角跟蹤曲線Fig.4 Attack angle tracking curve

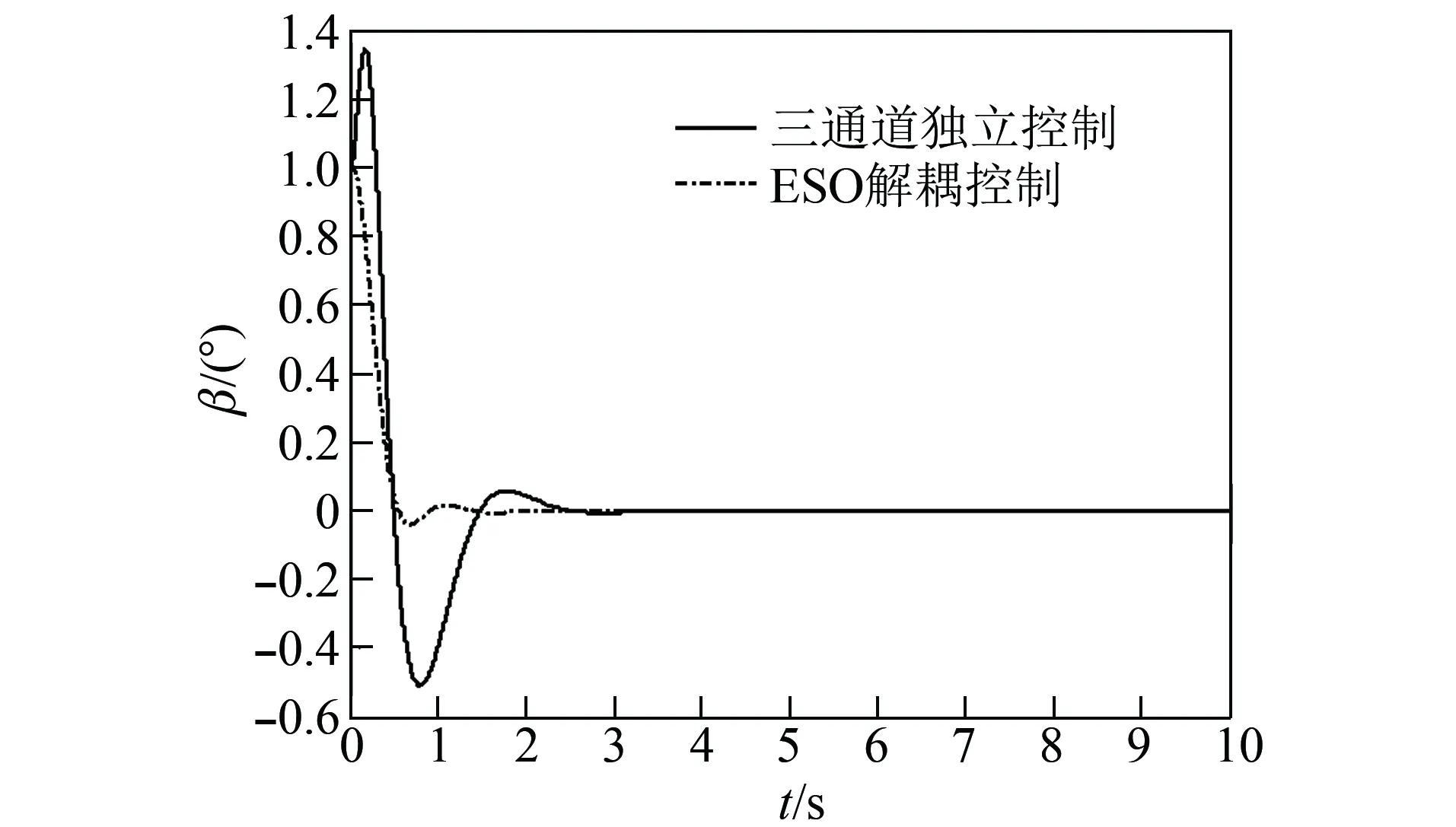
圖5 側滑角跟蹤曲線Fig.5 Sideslip angle tracking curve

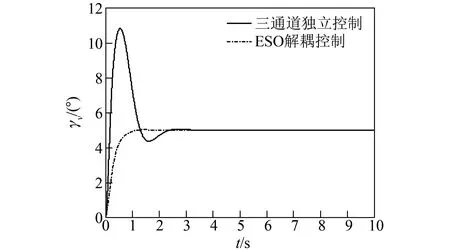
圖6 傾側角跟蹤曲線Fig.6 Heeling angle tracking curve

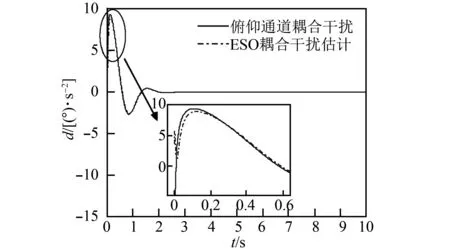
圖7 俯仰通道的ESO耦合干擾估計曲線Fig.7 ESO coupling interference estimation curve of pitching channel

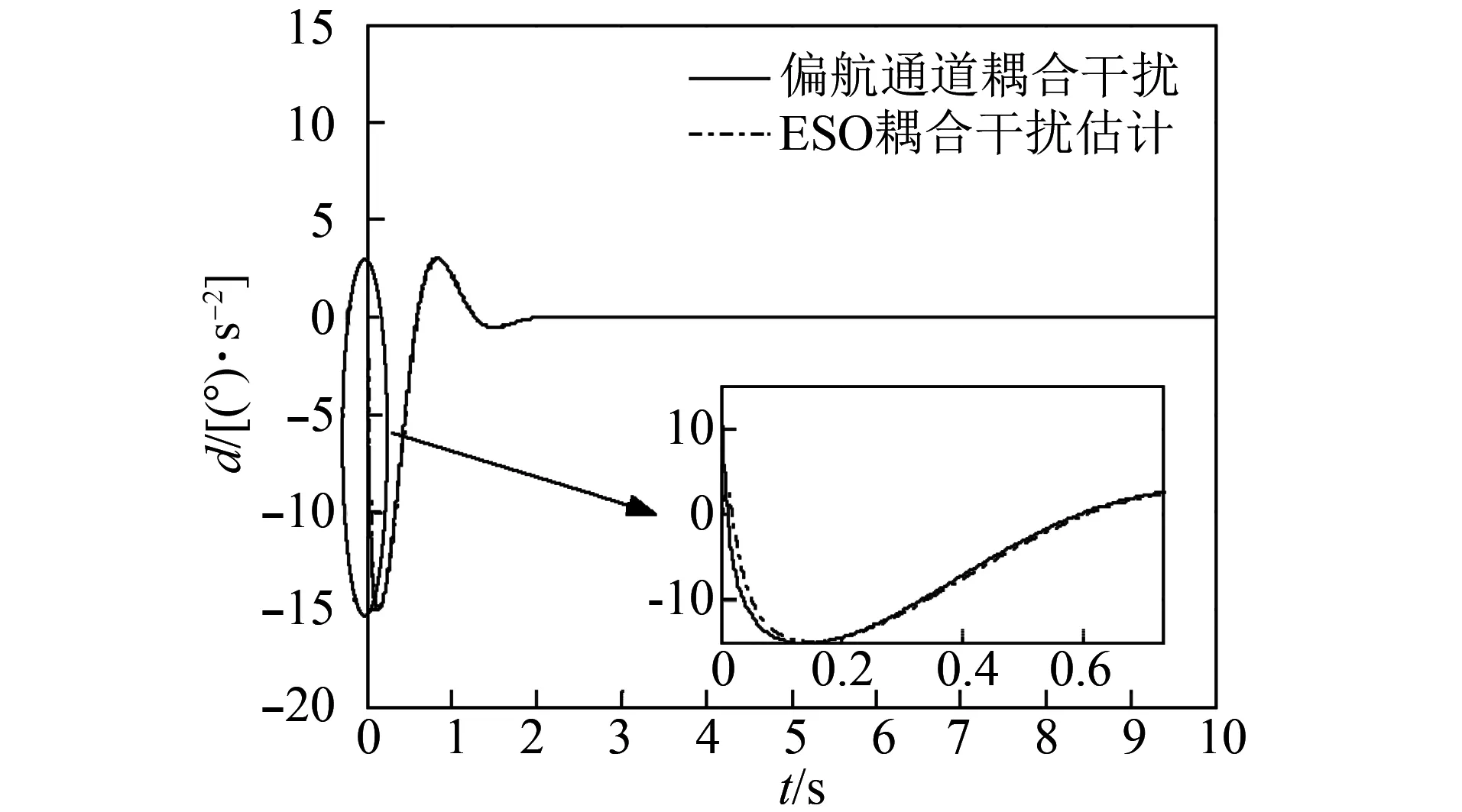
圖8 偏航通道的ESO耦合干擾估計曲線Fig.8 ESO coupling interference estimation curve of yaw channel

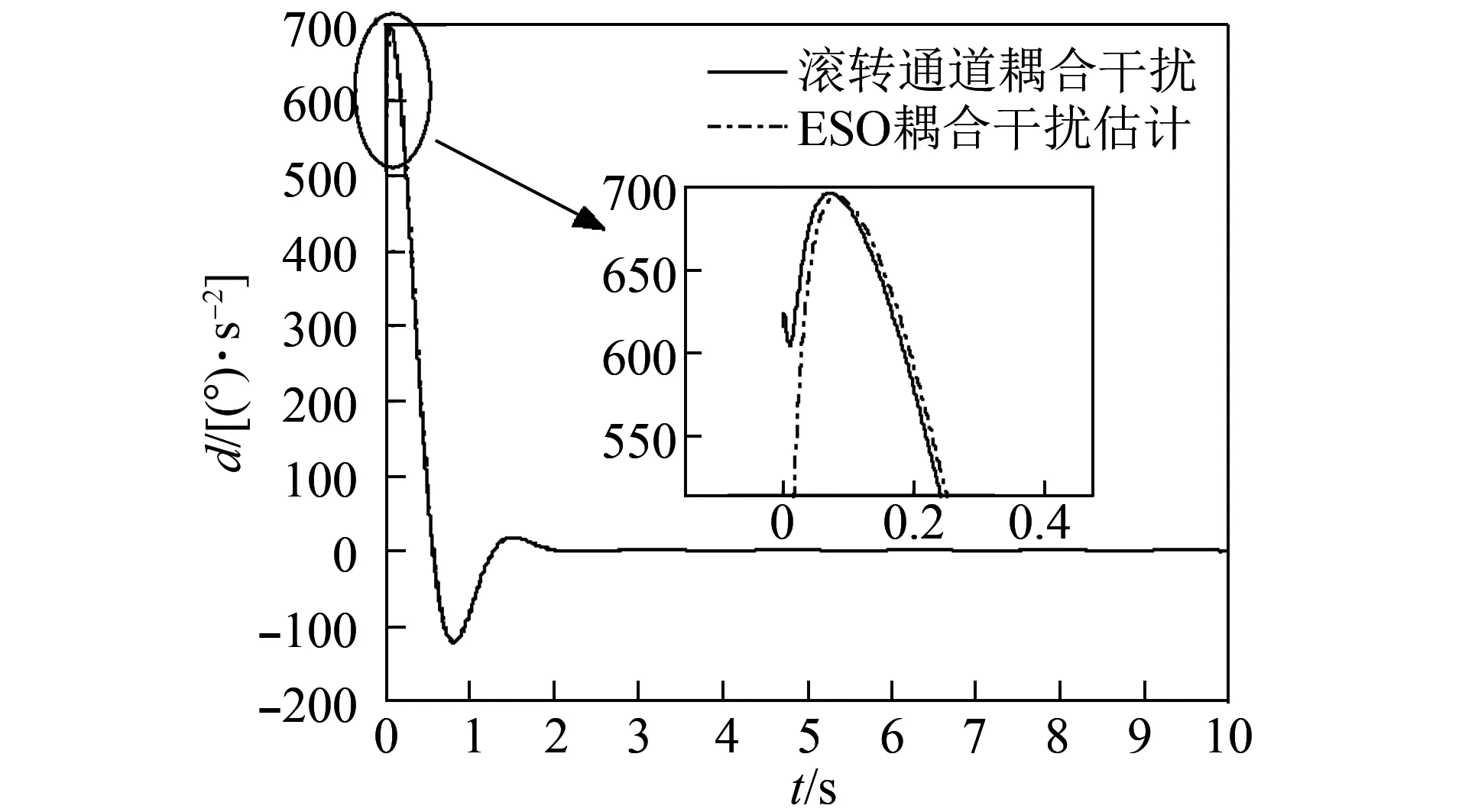
圖9 滾轉通道的ESO耦合干擾估計曲線Fig.9 ESO coupling interference estimation curve of rolling channel

3.3 仿真結果分析

1) 控制性能分析

圖4～圖6分別為攻角、側滑角和傾側角的跟蹤曲線，當初始側滑角不為零時，ESO解耦控制方法可使三通道輸出平穩、快速、較小的超調跟蹤指令信號。通過兩種方法對比曲線可以看出，三通道獨立控制方法跟蹤性能較差，充分體現出ESO解耦控制方法的性能優勢。

2) 解耦性分析

通過圖4～圖6可看出，三通道獨立控制中偏航通道和滾轉通道交連耦合嚴重，偏航通道的側滑角最大值約0.5°，超調約40%；滾轉通道最大值約11°，超調大于100%；俯仰通道受耦合影響較小。加入ESO解耦控制，耦合補償可大大降低耦合影響，俯仰通道最大值有所降低；偏航通道最大值約為0.02°，超調小于2%；滾轉通道不受超調影響。由此說明該方法可有效實現解耦控制。

3) ESO的觀測性能分析

圖7～圖9分別為ESO對三通道耦合干擾的估計曲線，由圖可知，ESO可較為精確地估計出耦合項干擾信號值，干擾信號值隨耦合項值的變化而實時改變，這得益于ESO這種精準的耦合干擾跟蹤。補償可減少耦合影響，達到解耦的目的。此外，ESO參數取值大即提高觀測器的帶寬，可提高一定觀測精度，但觀測器帶寬的增加會引入高頻噪聲，嚴重影響系統性能，故ESO參數即β01、β02取值要折中考慮。

通過控制設計和仿真分析，本文解耦控制方法由兩部分組成，一個是極點配置的狀態反饋控制，它主要影響系統的動態性能和穩定性；另一個是基于ESO的補償控制，它對耦合進行估計和補償，主要影響系統的解耦性能，當兩個控制方法協調匹配時控制效果最佳。從上述分析可知，本文設計驗證了基于ESO的多變量控制方法的正確性和有效性。

4 結束語

本文研究了基于ESO的BTT飛行器姿態控制系統的多變量解耦控制問題。BTT飛行器中側滑角不為零，飛行器控制系統三通道交連耦合嚴重。為解決此問題，用反饋機制建立能觀測耦合擾動作用的ESO，而它不依賴生成耦合擾動的具體數學模型，也無須直接測量其作用；利用已知設計控制器模型參數即可設計出擴張狀態觀測器，而不需要其他模型量。實現對耦合擾動的估計并對其進行補償，進一步設計獨立三通極點配置的閉環反饋控制器，完成多變量的解耦控制，是一種通用而實用的有效方法。通過數學仿真驗證了所設計的多變量解耦控制方法的正確性和有效性，為BTT飛行器多變量解耦控制提供一種新思路，此方法可用于解決飛機、航天飛機、BTT導彈及高超聲速飛行器等面對稱的耦合姿態控制問題，具有一定的工程實用價值。此方法未考慮參數攝動的魯棒性問題和參數變化的快時變問題，以及量測噪聲的影響，后續將進一步研究和討論。

[1] 葉振信, 傅維賢, 王萬軍, 等. 戰術導彈BTT控制技術發展綜述[J]. 航天控制, 2009, 27(5): 106-110.

[2] 張靖男, 趙興鋒, 鄭志強. BTT導彈的發展現狀與趨勢[J]. 飛航導彈, 2006(10): 37-39.

[3] 王凌艷, 呂鳴, 孫未蒙, 等. BTT導彈的解耦問題綜述[J]. 飛航導彈, 2009(6): 60-64.

[4] LEE C H, CHUNG M J. Gain scheduled state feedback control design technique for flight vehicles[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(1): 173-182.

[5] 童春霞, 王正杰, 張天橋. BTT導彈的變結構解耦控制系統設計[J]. 宇航學報, 2006, 27(1): 27-30.

[6] 張艷, 段朝陽, 張平, 等. 基于動態逆的BTT導彈自動駕駛儀設計[J]. 北京航空航天大學學報, 2007, 33(4): 422-426.

[7] 韓京清. 自抗擾控制技術[M]. 北京: 國防工業出版社, 2009.

[8] CASTANEDA L A, LUVIANO-JUAREZ A, CHAIREZ I. Robust trajectory tracking of a Delta robot through adaptive active disturbance rejection control[J]. IEEE Transactions on Control Systems Technology, 2015, 23(4): 1387-1398.

[9] ZHENG Q, GAO L Q, GAO Z Q. On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics[C]∥Proceedings of the 46th IEEE Conference on Decision and Control. New Orleans, LA, USA, 2007: 3501-3506.

[10] ZHU Z, XU D, LIU J, et al. Missile guidance law based on extended state observer[J]. IEEE Transactions on Industrial Electronics, 2013, 60(12): 5882-5891.

[11] GUO B Z, ZHAO Z L. On the convergence of an extended state observer for nonlinear systems with uncertainty[J]. Systems & Control Letters, 2011, 60(6): 420-430.

[12] ZHENG Q, GAO L Q, GAO Z Q. On validation of extended state observer through analysis and experimentation[J]. Journal of Dynamic Systems, Measurement, and Control, 2012, 134(2): 024505.

[13] 杜立夫, 黃萬偉, 楊廣慧, 等. 基于補償方法的高超聲速滑翔飛行器多變量輸出解耦控制[J]. 航天控制, 2015, 33(4): 40-45.

[14] 胡壽松. 自動控制原理[M]. 北京: 科學出版社, 2008.