改進字典學習的振動信號檢測方法

何 翔，高宏力，黃海鳳，文 剛

（西南交大通大學 機械工程學院，四川 成都 610031）

1 引言

軸承、齒輪、絲杠等旋轉機械在機械系統中應用極其廣泛，其運行狀態和故障與否直接影響整個機械系統的工作精度和壽命。而機械系統運行狀態信息的獲取是對系統狀態評估和故障檢測的前提。由于振動信號自身實時性、周期性以及加速度傳感器體積小，頻帶寬，易安裝，高頻響應穩定等特性，振動信號已經成為當前機械系統故障檢測中應用最廣泛的信息載體。尤其針對旋轉機械關鍵零部件，通過其振動信號實現故障檢測的方法極為普遍。所涉及的方法大致分為以下兩類：基于機器學習智能識別的方法和基于信號處理頻譜檢測的方法。

基于機器學習智能識別的方法是一種典型的通過數據特征驅動的方法，其對于信號的產生機理和系統的動力學模型并不深究，以人工神經網絡，支持向量機，樸素貝葉斯，最大期望，AdaBoost迭代和混合智能學習等算法為代表[1-2]，主要涵蓋了不同空間的特征提取，多維數據降維壓縮，統計學習等技術；基于信號處理頻譜檢測的方法通過分析比較其特征頻率來檢測系統和零部件不同的狀態和故障，相較于基于機器學習智能識別的方法，后者更注重機械系統結構和信號本質。檢測過程中，振動信號濾波去噪，即振動信號預處理是關鍵，也是信號處理領域的研究熱點和研究難點，其預處理效果往往直接決定了檢測方法的可行性和有效性。受到學術界認可且被廣泛應用的去噪方法通常是基于小波變換，經驗模態分解，譜峭度，盲源分離，自回歸模型等算法[3-6]，均取得了不錯的去噪效果，但也存在過度依賴于經驗知識和人工定參等局限性[7]。

針對上述問題，提出一種改進字典學習的振動信號檢測方法，區別于傳統去噪方法單純地減弱或消除振動信號噪聲成分，該方法是通過信號自身結構重構信號。該方法的主要原理是通過原始振動信號自身驅動數據構成訓練樣本，采用基于非負K奇異值分解（Non-negative K-SVD，NN-K-SVD）算法[8]迭代更新得到超完備字典和稀疏編碼，重構振動信號以實現預處理。最終提取重構信號的包絡譜實現故障檢測。

2 基于改進字典學習的去噪方法

2006年，文獻[9]論證了壓縮采樣理論，根據數據的可壓縮性，通過低維欠奈奎斯特數據實現高維采樣，極大地推動了字典學習在數據分類聚類，信息壓縮，圖像處理等領域的發展。近年來，該理論逐漸被引入機械系統故障檢測領域，由于基于該理論生成的重構信號更匹配原始振動信號的固有特性和結構，采用字典學習去噪效果顯著。

2.1 字典學習算法

字典學習的本質是一種通過構造字典和稀疏編碼循環迭代更新的算法。構造字典采用經驗基函數或者基于自身訓練，后者自適應更佳。K奇異值分解（K-Signal Value Decomposition，KSVD）是經典字典學習算法[10]，定義原始信號 X，字典 D∈Rm×k，每列對應原子d，稀疏編碼S，目標函數：

新一代稀疏編碼St通過正交匹配追蹤（Orthogonal Matching Pursuit，OMP）逼近得到，結合上一代更新的字典Dt-1表示信號X0，固定St求新一代字典Dt，交替迭代得到最終超完備字典D^和稀疏編碼S^。

式中：X^—重構信號；ε—噪聲成分。

提出的NN-K-SVD算法是K-SVD在非負條件下的改進，通過采用更稀疏的編碼來提取信號的局部特征，學習構造更匹配信號特性的字典。

稀疏編碼：采用非負基追蹤（Non-negativeBasisPursuit，NNBP）算法求解能量函數[11]

式中：?i，j：Xij≥0，Dij≥0，Sij≥0，?i，常數 λ＞0，表征

信號重構精度和稀疏性的相對數值關系。第一項求X-DS

的l2范數重構誤差，第二項是稀疏編碼懲罰項，約束稀疏分

布，確保能量函數逐步減小。

非負稀疏編碼的迭代方法：

式中：．×和．/—矩陣對應位置元素相乘除，即點乘和點除；（．）’—矩陣轉置。迭代后得到的稀疏編碼S非負，確保達到要求精度下得全局最小值。

字典更新：固定S，采用梯度下降法優化：

其中，迭代步長μ＞0，通過調整μ以滿足式（1）中目標函數，且d＜0時歸零確保D非負。

和K-SVD算法相同，NN-K-SVD算法通過交替迭代以更新字典和稀疏編碼，且得到的非負編碼具有更好的稀疏性，是一種有意義的字典學習改進。

2.2 字典學習去噪方法

故障檢測領域，原始振動信號通過改進的字典學習算法逼近信號本質結構。是基于改進字典學習的去噪方法的流程，如圖1所示。加速度傳感器以一定采樣頻率采集一維信號，以一定重疊率將其重疊分割得到列向量并構成訓練樣本X；初始化原始字典D并對生成的訓練樣本進行稀疏編碼得到S，通過采用上述NN-K-SVD算法交替迭代更新得到字典D^和對應的稀疏編碼S^；由式（2）通過最終得到的超完備字典D^和稀疏編碼S^計算得到更新樣本X^，逆疊加重構信號。重構信號相較原始信號去噪效果顯著。

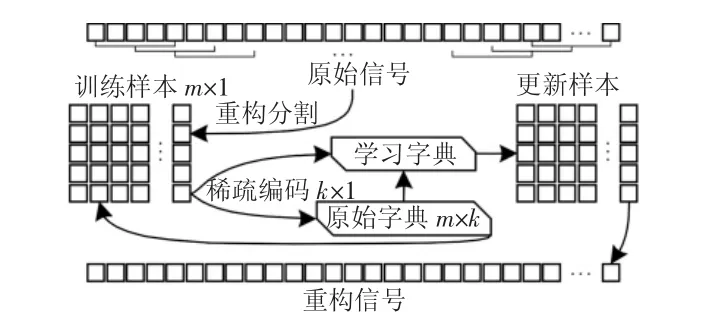
圖1 基于改進字典學習的去噪方法Fig．1 De-noising Method Based on Improved Dictionary Learning

3 仿真振動信號去噪分析

為驗證上述改進字典學習去噪方法的有效性，通過數學函數構建信號以仿真含有故障的機械系統的振動信號，正弦函數仿真基頻信號可以表示為：

式中：fr—主軸頻率。

故障表征的瞬態沖擊衰減信號可以表示：

式中：α—衰減率；f0—固有頻率；T—沖擊周期。

通過上述基頻信號和瞬態沖擊衰減信號并疊加高斯噪聲成分ω構成仿真信號，如圖2所示。仿真信號中噪聲成分基本覆蓋紅色表征的沖擊成分。

f（t）=a（t）+x（t）+ω（t）（8）

圖2 仿真信號Fig．2 Simulation Signal

基于改進字典學習的去噪方法預處理，構建包含2000個數據點的一維仿真信號，每隔5個數據點重疊分割得到包含80個數據點的385列向量構成訓練樣本。定義稀疏閥值為5，即稀疏編碼矩陣每一列非零元素不超過5。采用NN-K-SVD算法迭代更新20次最終生成（80×10）的學習字典和（10×385）的稀疏編碼，矩陣相乘并逆疊加得到去噪后的重構信號。為驗證方法優越性，分別采用小波變換（WaveletTransform，WT）和K-SVD算法對信號去噪。如圖3所示。

圖3 去噪信號Fig．3 De-Noised Signal

自上而下分別為通過WT、K-SVD和NN-K-SVD算法對上述含噪聲的仿真信號進行預處理后得到的增強信號。對比WT算法和K-SVD算法，由于字典學習算法基于信號自身固有特性和結構驅動信號預處理，從圖中不難發現后者去噪效果更加明顯，引入互相關系數R，如表1所示。定量對比R的大小結果亦然。

式中：cov（.）—x和y的協方差；σ—標準差。將無噪信號和去噪信

號代入，R越接近1，去噪效果越好。

表1 互相關系數對比Tab.1 Comparison of Cross Correlation Coefficient

對比K-SVD算法和NN-K-SVD算法，后者改進添加了非負約束條件，實現信號局部特征提取，對比編碼中非零元素數量，NN-K-SVD算法的編碼更稀疏，有利于數據壓縮，且優化和簡化算法，如表2所示。

表2 稀疏編碼非零元素對比Tab.2 Comparison of Non-zero Sparse Coding

4 實驗振動信號故障檢測

為驗證改進字典學習的振動信號檢測方法有效性，采用美國國家科學基金項目加州大學河濱分校智能維護系統中心的軸承數據[12]設計驗證實驗。

交流電機由傳送帶驅動主軸以轉速2000r/min運行，主軸安裝軸承，如圖4所示。軸承2和軸承3負載26.7kN，采樣頻率20kHz，通過采集卡NI6062E控制安裝于軸承座的加速度傳感器PCB353B33采集全部軸承的振動信號。通過大量實驗使機械系統性能退化，軸承出現故障，如表3所示。由式算得到軸承內圈、外圈、滾動體和保持架故障特征理論頻率。

圖4 實驗臺示意圖和實物圖Fig.4 Sketch Map and Physical Map of Experiment Rig

式中：fr—主軸頻率表征主軸轉速；Z—滾動體數量；α—接觸角；d—滾動體直徑；D—節徑。

表3 軸承Rexnord ZA-2115參數Tab.3 Bearing Parameters of Rexnord ZA-2115

選取實驗數據集2中末端信號進行處理，信號包含數據點20480個，故障檢測顯示軸承1外圈故障。由式（10）得到軸承理論外圈故障頻率236.2 Hz。

基于提出的改進字典學習的振動信號檢測方法對信號進行故障檢測。隨機截取實驗數據集2中末端某一信號中的2048個數據點，如圖5所示。根據表中參數基于改進的字典學習去噪方法重構信號，實現軸承振動信號預處理，如表4所示。

表4 去噪參數定義Tab.4 Definition of De-noising Parameters

由于包絡對信號中和沖擊相關成分極其敏感，采用準正交采樣，即4倍采樣后求相鄰數據點平方和以提取非負重構信號的幅值包絡，實現沖擊頻率量化，如圖5所示。從得到的包絡信號中不難發現由于軸承故障所生成的瞬態沖擊成分。通過傅里葉變換提取包絡信號頻譜，在頻域中檢測軸承故障。

重構信號包絡譜能清晰地檢測沖擊頻率及其倍頻，如圖6所示。其峰值即故障頻率約為236Hz，和上述軸承理論外圈故障頻率236.2Hz基本吻合。

圖6 重構信號包絡譜和基于AR和小波算法包絡譜Fig.6 Spectral Envelope of Two Kinds of Algorithm

為驗證振動信號檢測方法有效性，采用AR模型和小波變換對同一信號去噪，并通過希爾伯特變換和傅里葉變換求信號包絡譜，如圖6所示。去噪得到的包絡譜的故障頻率和提出方法所得到故障頻率一致，但沖擊特征相對不夠突出。因此，改進字典學習的振動信號檢測方法不但編碼更稀疏，有利于信號壓縮，且去噪效果具有一定先進性。

5 結語

針對傳統檢測方法，提出了一種改進字典學習的振動信號檢測方法，通過信號自身結構在非負條件下字典學習實現預處理。仿真瞬態沖擊信號和設計軸承故障實驗中，采用基于NN-K-SVD算法的檢測方法對信號去噪，能有效提取故障頻率，且效果顯著，較傳統方法自適應強，去噪效果佳。結果表明，改進字典學習的振動信號檢測方法適用于故障檢測，為振動信號濾波去噪提供了新思路，為基于振動信號實現機械系統智能維護提供了參考。

［1］胡耀斌，厲善元，胡良斌.基于神經網絡的滾動軸承故障診斷方法的研究［J］.機械設計與制造，2012（2）：187-189.（Hu Yao-bin，Li Shan-yuan，Hu Liang-bin.Fault diagnosis of rolling bearing based on neural network［J］.Machinery Design&Manufacture，2012（2）：187-189.）

［2］袁浩東，陳宏，侯亞丁.基于優化支持向量機的軸承故障診斷方法研究［J］.機械設計與制造，2012（5）：118-120.（Yuan Hao-dong，Chen Hong，Hou Ya-ding.Research on the Fault Diagnosis of Rolling Bearing Based on Optimized SVM［J］.Machinery Design&Manufacture，2012（5）：118-120.）

［3］Al-Badour F，Sunar M，Cheded L.Vibration analysis of rotating machinery using time-frequency analysis and wavelet techniques［J］.Mechanical Systems and Signal Processing，2011，25（6）：2083-2101.

［4］蔡艷平，李艾華，石林鎖.基于EMD與譜峭度的滾動軸承故障檢測改進包絡譜分析［J］.振動與沖擊，2011，30（2）：167-172.（Cai Yan-ping，Li Ai-hua，Shi Lin-suo.Roller bearing fault detection using improved envelope spectrum analysis based on EMD and spectrum kurtosis［J］.Journal of Vibration and Shock，2011，30（2）：167-172.）

［5］Ricardo A，Salido R，Radu R.EEG montage analysis in the blind source separation framework［J］.Biomedical Signal Processing and Control，2011，33（1）：77-84.

［6］Cheng J S，Yu D J，Yang Y.A fault diagnosis approach for roller bearings based on EMD method and AR model［J］.Mechanical Systems and Signal Processing，2006，20（2）：350-362.

［7］Christian D.Sigg，Tomas Dikk，Joachim M.Buhmann.Speech enhancement with sparse coding in learned dictionaries［C］.ICASSP，2010：4758-4761.

［8］Michal Aharon，Michael Elad，Alfred M.K-SVD and its non-negative variant for dictionary design［C］.Proceeding of SPIE，2005：5914.

［9］Candes E J，Tao T.Near-optimal signal recovery from random projections：universal encoding strategies［J］.IEEE Trans.Info.Theory，2006，52（12）：5406-5425.

［10］Michal Aharon，Michael Elad，Alfred M.Bruckstein.The K-SVD：An algorithm for designing of over-complete dictionaries for sparse and representation［J］.IEEE Transactions on Signal Processing，2006，54（11）：4311-4322.

［11］P.O.Hoyer.Non-negative sparse coding［C］.Neural Networks for Signal Processing XII（IEEE Workshop on Neural Networks for Signal Processing），2002：557-565.

［12］Hai Qiu，Jay Lee，Jing Lin.Wavelet filter-based weak signature detection method and its application on roller bearing prognostics［J］.Journal of Sound and Vibration，2006（289）：1066-1090.