認知星地混合網絡中基于能效最大化的最優功率控制方法*

汪 晴，石盛超，邊東明，朱宏鵬，唐璟宇

0 引 言

衛星通信覆蓋范圍廣、應用場景多樣，在未來的無線通信網絡中扮演著越來越重要的角色。特別是在偏遠地區和應急通信、救災場合，衛星通信相較于地面系統的優越性更加明顯[1]。但是，隨著寬帶多媒體業務的逐漸增多，衛星通信系統中頻譜資源緊缺的問題愈發明顯。為了解決這個問題，研究人員展開了很多切實有效的研究。其中，將認知無線電（Cognitive Radio，CR）技術[2]應用到衛星通信系統被認為是一項很有前景的工作[3]。

在眾多的認知技術中，由于易于實現且可得到較高的頻譜效率，underlay技術被廣泛應用于各種認知無線電網絡中。這種技術中，主用戶可以和次級用戶同時工作在同樣的頻段上[4-5]。但是，要使用underlay技術必須滿足一個前提：次級用戶的工作不會影響主用戶的正常工作，即次級用戶帶來的干擾必須維持在一個能夠接受的門限以下。所以，次級用戶的功率控制問題是認知網絡亟需解決的問題。當衛星系統作為次級用戶系統時，文獻[6-7]研究了上行鏈路場景下衛星用戶的最優功率控制問題，其中的主用戶系統分別是地面移動系統和地面固定業務系統。當衛星作為主用戶系統時，文獻[8]研究了在下行鏈路條件下，地面次級用戶的功率控制問題。但是，文獻[8]中的目標函數選擇的是有效容量。隨著綠色通信概念的產生，人們越來越關注通信系統中的環境影響和能量消耗問題[9]。文獻[10]解決了通信衛星中的最佳能量分配和接入控制問題。文獻[11]研究了多波束衛星中下行鏈路的高能效功率分配問題。但是，對于認知星地混合網絡中的高能效功率控制問題，現在還很少有相關的研究工作。

正是基于以上研究背景，在認知星地混合網絡場景下，當衛星系統作為主用戶系統、地面移動系統作為次級用戶系統時，本文針對下行鏈路場景中的地面次級用戶，提出了兩種基于能效最大化的功率控制方法。為了保證衛星用戶的通信質量，使干擾功率維持在一個可以接受的門限以下，算法選取平均干擾功率（Average Interference Power，AIP）約束條件。對于次級用戶的功率約束，兩種算法分別選取了平均發射功率（Average Transmit Power，ATP）和峰值發射功率（Peak Transmit Power，PTP）約束。最后的仿真結果對比了兩種算法的性能，分析了功率約束門限、地面干擾鏈路條件和衛星干擾鏈路條件對最終算法性能的影響，為認知星地混合網絡中高能效功率分配方式提供了著實有效的指導和參考。

1 系統模型

本文研究的認知星地混合網絡結構如圖1所示，衛星通信系統為主用戶系統，地面移動系統為次級用戶系統，這里主要考慮下行鏈路場景，衛星用戶為移動終端。關于認知技術的選擇，根據前文所述，本文選擇underlay的頻譜共享方式。

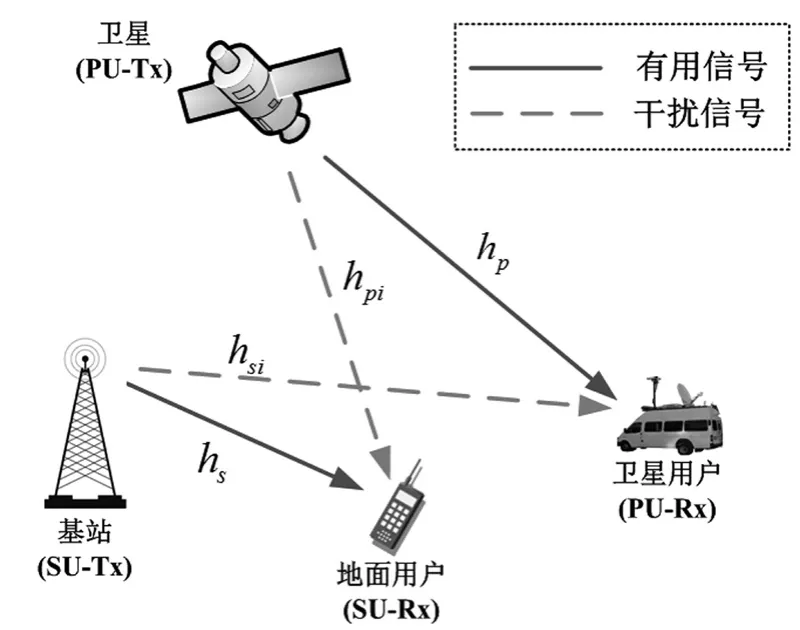
圖1 認知星地混合網絡系統模型

圖1 中，hp和hpi分別是衛星主用戶鏈路和衛星干擾鏈路的鏈路增益，hs和hsi則為地面次級用戶鏈路和次級用戶干擾鏈路的鏈路增益。對于衛星鏈路，由于本文的衛星用戶為移動終端，所以hp和hpi可以用陰影萊斯信道（Shadowed Rice Channel）進行描述[12]，即hp和hpi的概率密度函數可以表示為：

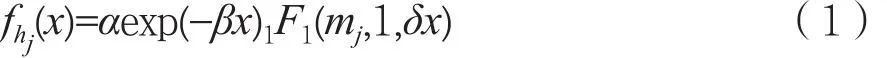
其中，j為 p 或者 pi；1F1(·,·,·)為合流超幾何函數[13]，而α、β和δ可以計算：

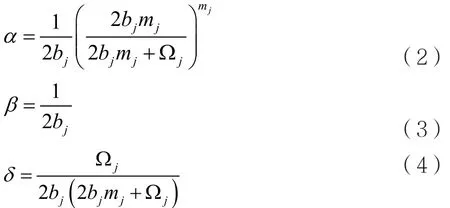
其中，2bj為散射分量的平均功率，Ωj為直射分量的平均功率，mj為Nakagami衰落因子。

至于地面鏈路增益hs和hsi，本文考慮Nakagami衰落信道[8]，概率密度函數為：

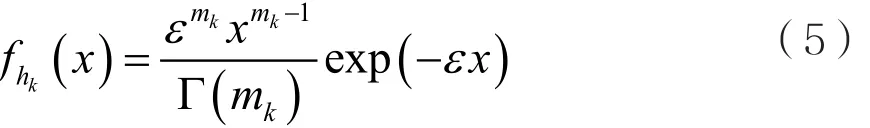
其中，k為s或者 si；Γ(·)為 Gamma函數[13]，mk為Nakagami衰落因子，Ωk為信號的平均功率；ε等于mk/Ωk。此外，本文假設次級用戶具有理想的信道狀態信息（Channel State Information，CSI）。

2 基于能效最大化的功率控制

在衰落信道場景下，能效（Energy Efficiency）通常定義為平均通信速率和平均功率消耗的比值。具體到本文研究，通過計算遍歷容量（Ergodic Capacity）和平均功率消耗的比值來獲得系統能效[14]。為了不影響主用戶的正常工作，必須限制對次級用戶造成的干擾。使用較多的兩種干擾功率約束指標為平均干擾功率（Average Interference Power，AIP）約束和峰值干擾功率（Peak Interference Power，PIP）約束。根據文獻[15]的研究成果：相比于PIP約束，AIP不僅可以更好地保護主用戶通信質量，而且可以獲得更高的通信容量。所以，本文的功率控制方案中選擇AIP約束作為干擾功率的約束條件。為了進一步控制地面次級用戶的發射功率，本文提出的兩種功率控制方案還分別引入了平均發射功率（Average Transmit Power，ATP）約束和峰值發射功率（Peak Transmit Power，PTP）約束。

2.1 ATP約束的功率控制

ATP約束的功率控制方案中，能效最大化問題可以描述為：

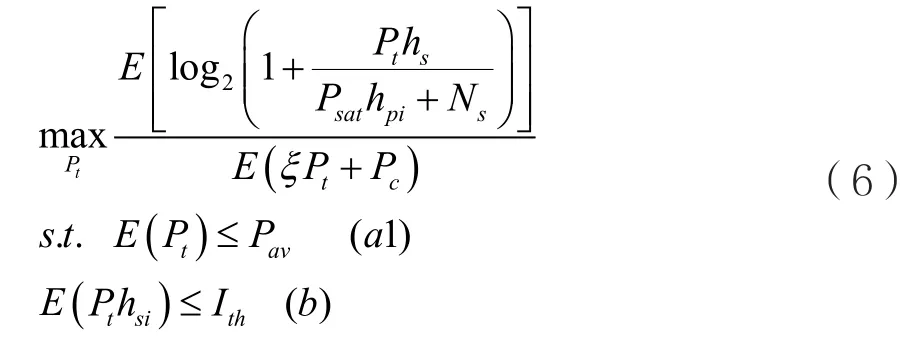
其中，Pt為地面次級用戶的發射功率，Psat為衛星的發射功率，Ns為噪聲功率，ξ和Pc分別表示功率放大器系數和固定環路功率損耗，E(·)代表計算期望值，Pav和Ith分別為ATP約束和AIP約束的門限值。

可以證明，式（6）是一個非線性凹的分數規劃問題[16]。根據Dinkelbach’s方法[17]的結論，可以將式（6）等效為以下問題求解：

其中，η為非負參數，S1={Pt|Pt∈(a1)∩(b)}。可以證明，這是一個凸優化問題，可以通過Lagrange對偶算法進行求解[16]。

首先，寫出式（7）對應的Lagrange函數：

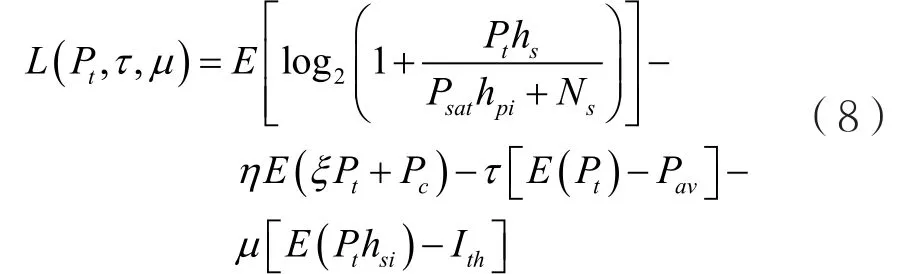
τ和μ是對應于約束條件(a1)和(b)的Lagrangian乘子，所以（7）對應的Lagrange對偶函數為：

對偶問題可以表示為：

類似于文獻[15]，根據對偶分解原理[16]，問題（10）可以被分解為多個平行的子問題。這些子問題具有相同的結構，且每個子問題對應一個衰落信道狀態。所以，當信道衰落狀態給定后，相應的子問題可以描述為：

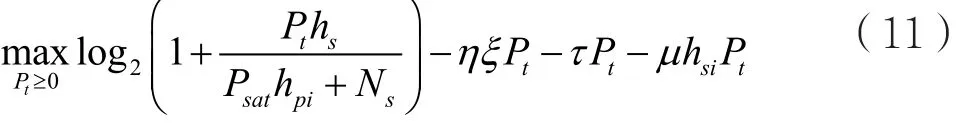
首先固定τ和μ，然后迭代求解所有衰落狀態對應的子問題（11），進而利用子梯度方法[16]更新τ和μ，就可以實現求解，得到全局最優值，即式（7）對應的最優發射功率P*t為：

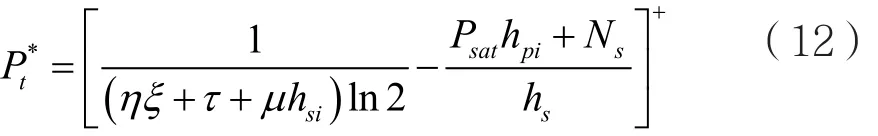
其中，[x]+=max(0,x)，表示取0和x之間的最大值。通過觀察結果可以發現，只要給定η，就可以得到最優發射功率。為了進一步得到最優能效值，本文使用Dinkelbach’s方法，并在此基礎上提出一種迭代功率分配方法求解式（6），得到最優能效值η*。具體的算法細節為：

設置迭代算法精度參數：ε1＞0，ε2＞0，t1＞0，t2＞0，Ni；

初始化系數：η=η0，τ=τ0，μ=μ0；

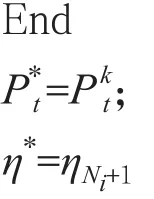
2.2 PTP約束的功率控制

當采用PTP約束時，能效最大化問題可以描述為：

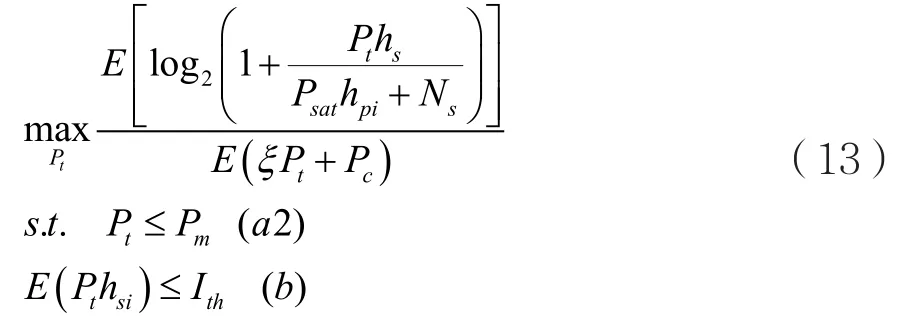
其中，Pm為PTP約束的功率門限值。問題（13）同樣是一個非線性凹的分數規劃問題[16]，仍然可以使用Dinkelbach’s方法進行求解。首先，得到對應的參數優化問題：

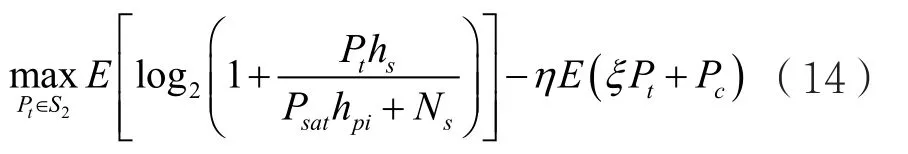
其中，S2={Pt|Pt∈(a2)∩(b)}。類似地，仍然可以使用Lagrange對偶算法式（14）進行求解。通過對偶分解后，每個衰落狀態對應的子問題可以描述為：

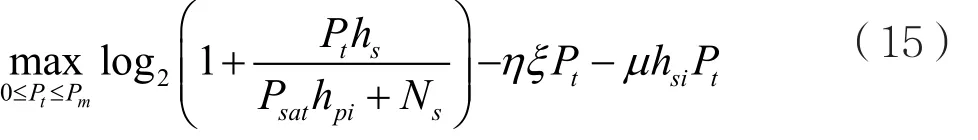
通過迭代求解所有衰落狀態的子問題和結合子梯度方法來對Lagrangian乘子μ進行更新后，可以完成求解，得到發射功率：

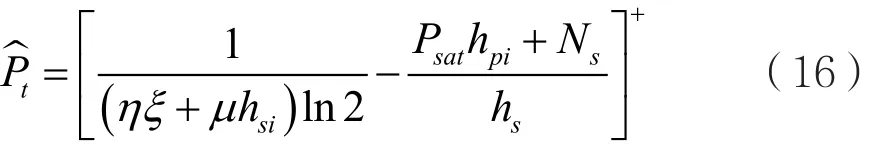
進一步考慮式（13）中的約束條件(a2)，最終得到最優發射功率：

為了尋找求解最優能效值，仍然可以使用本文提出的迭代算法進行搜索，但要對算法進行適當修改，主要包括兩點：（1）利用式（17）而不再是式（12）計算；（2）只有一個Lagrangian乘子μ需要進行更新。

3 仿真結果與討論

這一部分將對本文提出的兩種功率控制方法的性能進行仿真，并分析不同參數對最終結果的影響。仿真中使用的主要參數如表1所示，沒有特別說明，這些參數將保持不變。另外，所有仿真結果都是利用Monte Carlo仿真得到，實驗次數為5 000次。

表1 主要仿真參數取值

圖2給出了兩種功率控制方法在不同約束指標下，次級用戶能量效率隨著迭代搜索算法中Ni的變化曲線。仿真中，地面信道參數取值為ms=msi=1，Ωs=1，Ωsi=0.5；衛星干擾信道參數為bpi=0.126，mpi=10.1，Ωpi=0.835[12]。仿真結果表明，兩種功率控制方法不論在什么約束條件下，次級用戶能效都能實現收斂，從而證明了本文所提出的迭代搜索算法的有效性；進一步觀察可知，當迭代次數超過3后，最終結果就可以實現收斂，可見算法同時具有高搜索效率。

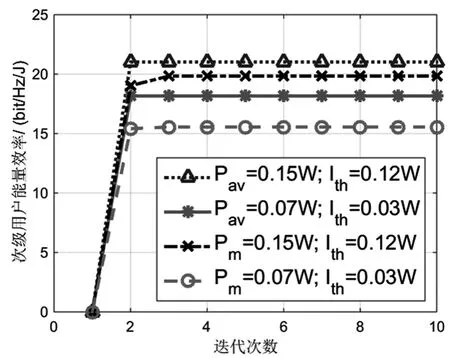
圖2 次級用戶能量效率隨著算法迭代次數的變化曲線

圖3 給出了兩種功率控制方法在不同發射功率約束條件下，次級用戶能效隨著Ith的變化曲線，其中信道參數的取值與圖2仿真所取的數值一致。結果表明，不論Pav/Pm取什么數值，使用ATP約束的功率控制方法性能總是優于使用PTP約束的功率控制方法。此外，隨著Pav/Pm的提高，兩種功率控制方法的性能都相應隨著提升。另外，隨著Ith的提高，次級用戶的能效逐漸增加，進而達到一個飽和值后不再變化，這是因為在Ith較小時，對次級用戶發射功率起主要約束作用的是AIP約束，但隨著Ith的逐漸增大，AIP約束將不再起作用，次級用戶的發射功率主要由ATP/PTP約束決定。

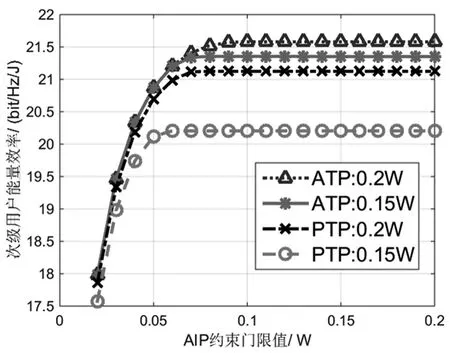
圖3 次級用戶能量效率隨著Ith的變化曲線

圖4 給出的是在不同的衛星干擾鏈路信道條件下，兩種功率控制方法中次級用戶能效隨著Ith的變化曲線。在這個仿真里，本文選取文獻[12]中的兩種經典衛星衰落信道場景：Average Shadowing場景（bpi=0.126，mpi=10.1，Ωpi=0.835） 和 Infrequent Light Shadowing場 景（bpi=0.158，mpi=19.4，Ωpi=1.29）。仿真結果表明，衛星干擾鏈路的信道條件越好，次級用戶的能效越低，即衛星干擾鏈路信道條件的改善不利于次級用戶性能。類似地，在同樣的衛星鏈路條件下，使用ATP約束的功率控制方法要優于使用PTP約束的方法。

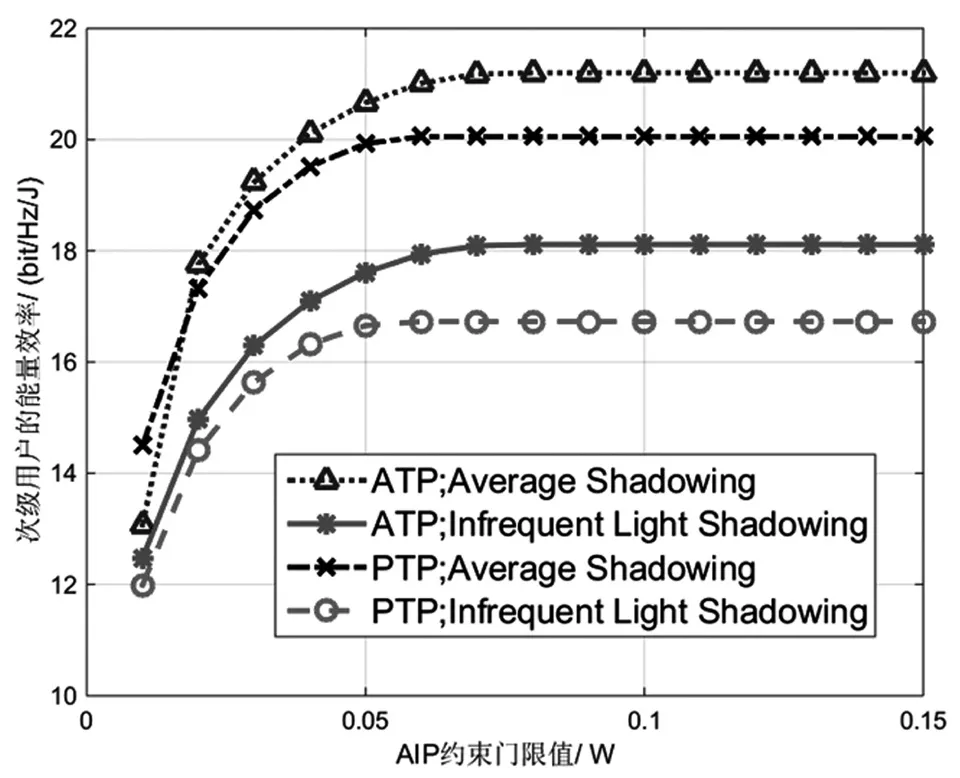
圖4 不同衛星干擾鏈路信道條件下次級用戶能效隨著Ith的變化曲線

圖5 給出了在不同的地面干擾鏈路信道條件下，兩種功率控制方法中次級用戶能效隨著Ith的變化曲線。這個仿真中，衛星鏈路選擇為Average Shadowing場景，Ωs=1，ms=msi=1。Ωsi越大，表示地面干擾鏈路的信道條件越好，對應的次級用戶能效值越小，即地面干擾鏈路信道條件的改善同樣不利于次級用戶的性能。此外，在同一種功率控制方法中，不論Ωsi取什么數值，最終次級用戶能效的收斂值都相同。這是因為當Ith足夠大時，能效值才會收斂，而此時AIP約束已經對次級用戶沒有影響，這和圖3得到的結論一致。

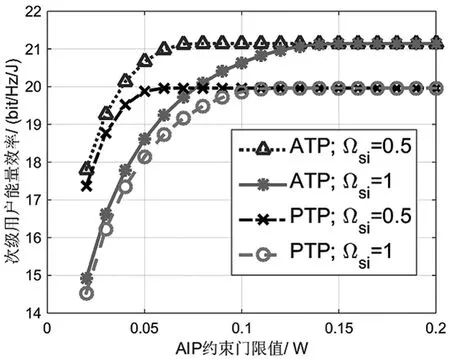
圖5 不同地面干擾鏈路信道條件下次級用戶能效隨著Ithfalse的變化曲線

4 結 語

本文針對認知星地混合網絡中地面次級用戶的功率控制問題，提出了兩種基于能效最大化的最優功率控制方法，分別選取ATP和PTP約束條件。為了保證衛星主用戶的通信質量，采取AIP約束。結合Dinkelbach’s方法和Lagrange對偶方法，求解得到最優發射功率的閉合表達式，并提出了一種新的迭代搜索算法，實現了對最佳能效的高效查找。仿真結果證明，搜索算法具有有效性和高效性，并分析了功率約束門限、地面干擾鏈路信道條件和衛星干擾鏈路條件對系統最終性能的影響作用，且所得結論為認知星地混合網絡中綠色通信場景下的功率控制問題提供了有效參考和指導。但是，本文的研究是在鏈路條件已知且理想的前提下開展的，面對非理想信道狀態信息的場景，仍然需要開展進一步的研究工作。

[1] 郭慶,王振永,顧學邁.衛星通信系統[M].北京:電子工業出版社,2010:1-9.GUO Qing,WANG Zhen-yong,GU Xue-mai.Satellite Communication System[M].Beijing:Publishing House of Electronics Industry,2010:1-9.

[2] Mitola J,Maguire G Q.Cognitive Radio:Making Software Radios More Personal[J].IEEE Personal Communicatio ns,1999,6(04):13-18.

[3] Sharma S K,Chatzinotas S,Ottersten B.Cognitive Radio Techniques for Satellite Communication Systems[C].IEEE 78th Vehicular Technology Conference(VTC Fall),2013:1-5.

[4] Haykin S.Cognitive Radio:Brain-empowered Wireless Communications[J].IEEE Journal on Selected Areas in Communications,2005,23(02):201-220.

[5] Goldsmith A,Jafar S A,Maric I,et al.Breaking Spectrum Gridlock with Cognitive Radios:An Information Theoretic Perspective[J].Proceedings of the IEEE,2009,97(05):894-914.

[6] Vassaki S,Poulakis M I,Panagopoulos A D.Optimal iSINR-based Power Control for Cognitive Satellite Terrestrial Networks[J].Transactions on Emerging Telecommunications Technologies,2017,28(02):1-10.

[7] Lagunas E,Maleki S,Chatzinotas S,et al.Power and Rate Allocation in Cognitive Satellite Uplink Networks[C].IEEE ICC,2016:1-6.

[8] Vassaki S,Poulakis M I,Panagopoulos A D,et al.Power Allocation in Cognitive Satellite Terrestrial Networks with QoS Constraints[J].IEEE Communications Letters,2013,17(07):1344-1347.

[9] CHEN Y,ZHANG S,XU S,et al.Fundamental Trade-offs on Green Wireless Networks[J].IEEE Communications Magazine,2011,49(06):30-37.

[10] FU A C,Modiano E,Tsitsklis J N.Optimal Energy Allocation and Admission Control for Communications Satellites[J].IEEE/ACM Transactions on Networking,2003,11(03):488-500.

[11] Qi T,WANG Y.Energy-efficient Power Allocation over Multibeam Satellite Downlinks with Imperfect CSI[C].IEEE WCSP,2015:1-5.

[12] Abdi A,Lau W C,Alouini M S,et al.A New Simple Model for Land Mobile Satellite Channels:First-and Secondorder Statistics[J].IEEE Transactions on Wireless Comm unications,2003,2(03):519-528.

[13] Gradshtevn I S,Ryzhik I M.Table of Integrals,Series,and Products[M].Seventh Edition.Elsevier,2007:820.

[14] WANG L,SHENG M,WANG X,et al.Mean Energy Efficiency Maximization in Cognitive Radio Channels with PU Outage Constraint[J].IEEE Communications Letters,2015,19(02):287-290.

[15] ZHANG R.On Peak Versus Average Interference Power Constraints for Protecting Primary Users in Cognitive Radio Networks[J].IEEE Transactions on Wireless Comm unications,2009,8(04):2112-2120.

[16] Boyd S,Vandenberghe L.Convex Optimization[M].Cambridge:Cambridge University Press,2004:127-129.

[17] Dinkelbach W.On Nonlinear Fractional Programming[J].Management Science,1967,13(07):492-498.