抑制風電爬坡事件的雙蓄電池組參數優化配置

，(.國網安徽省電力公司調度通信中心，安徽 合肥 3006；.合肥工業大學電氣與自動化工程學院, 安徽 合肥 30009)

0 引 言

大規模風電并網引起電網功率波動[1-2]，為了有效平抑波動，在并網系統中加入儲能裝置以減少棄風及彌補缺額。

風電功率持續波動，單一蓄電池組儲能系統(battery energy storage system,BESS)[3-4]存在充放電頻率過高和滿充滿放的問題。這里采用雙BESS[5]配置，兩組蓄電池采用同步或異步控制策略進行交替充放電，改善了平抑效果。采用同步控制[6]時，兩組蓄電池始終分別處于充、放電狀態，可以及時響應波動極端的情況，但BESS的容量無法充分利用，造成成本增加；采用異步控制時，蓄電池可同時處于充電或放電狀態來充分利用BESS的容量，但蓄電池組都處于充電狀態時無法響應風電缺額。

風電爬坡事件是一種短時間尺度下的大幅波動，往往發生在切入風速至額定風速段和切出風速段，對蓄電池充放電過程有很大的沖擊。風-儲系統棄風對電網無沖擊，而缺額只能依靠電網中其他發電設備彌補。合理規劃棄風和缺額，充分利用風能資源實現經濟最大化。

文獻[7]研究了風電爬坡率與儲能結合的優化控制，采用最佳荷電狀態的方式進行優化，但未考慮精確的風電爬坡模型。文獻[8-9]分別提出風-儲系統的聯合調度模型和基于正態分布的容量估算法，但未考慮儲能系統的經濟效益。

上述文獻中，未結合風電爬坡事件、BESS控制策略和棄風經濟性研究。下面綜合考慮BESS運行條件，蓄電池采用同步與異步控制策略，以蓄電池的裝置費用和使用壽命以及棄風缺額懲罰費用為目標函數，以風電場和BESS安全運行為約束條件，同時以功率波動越限概率和幅值為評價指標，采用IPSO算法優化配置BESS的額定容量及功率，降低風電場功率波動對電網的沖擊，降低系統成本。算例對比不同爬坡事件定義的適用性、同步與異步控制策略的優劣性，分析棄風因素的經濟性。

1 風-儲并網系統模型

風電場側裝設兩組蓄電池，風-儲并網系統結構如圖1，并網的輸出功率滿足：

Psys(t)=Pwt(t)-ΔPloss(t)+PB(t)

(1)

式中：Psys(t)為t時刻并網點的輸出功率；Pwt(t)為t時刻風電場的輸出功率；△Ploss(t)為t時刻風電系統的損耗功率；PB(t)為t時刻BESS的總輸出功率，PB(t)≥0時，蓄電池放電；當PB(t)<0時，蓄電池充電。PB1(t)、PB2(t)為BESS1、BESS2t時刻的輸出功率。

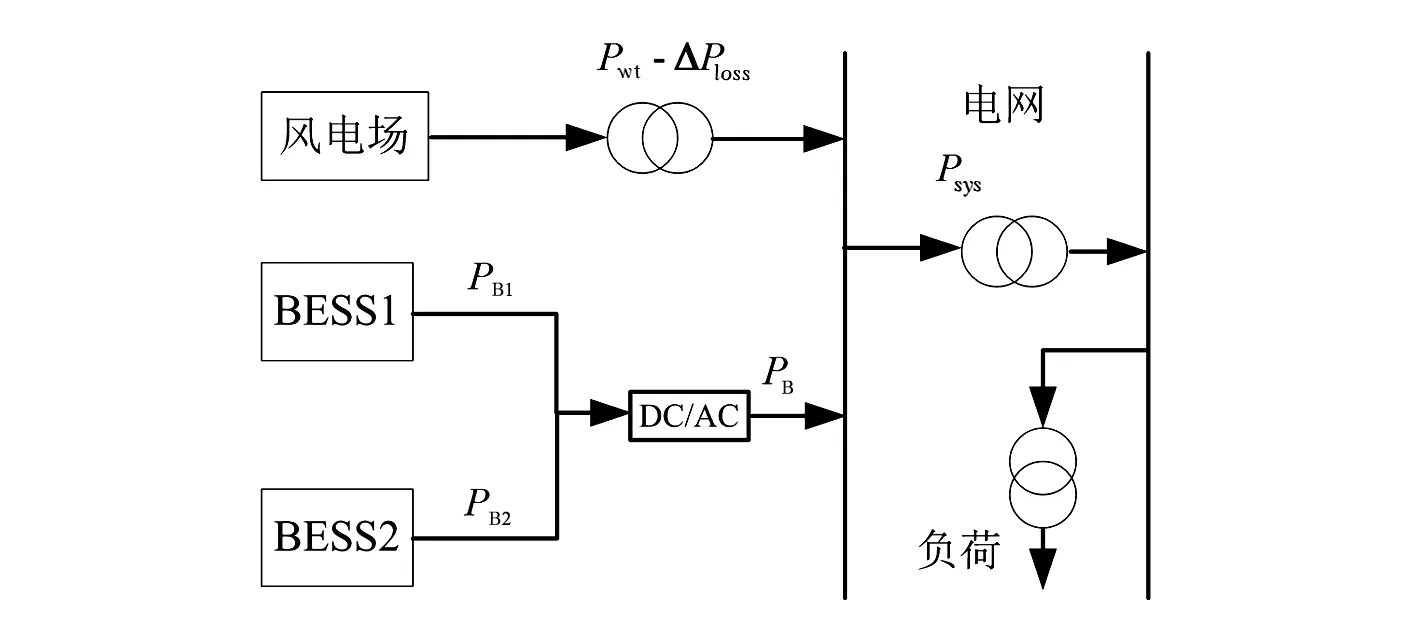
圖1 風-儲并網系統結構

BESS的平抑效果不要求輸出為一條平穩的直線，只要滿足國家風電并網標準[10-11]要求即可。

ΔPS(t)=|Psys(t)-Psys(t-Δt)|≤Pval

(2)

式中：ΔPS(t)為t時刻與相鄰(t-Δt)時刻的功率差；Δt為采樣時間間隔；Pval為并網功率波動限幅。

2 風電爬坡事件

當輸出功率波動幅值大于波動限幅Pval時，認為發生爬坡事件，定義爬坡幅值：

1)t時刻和(t-Δt)時刻

ΔPwt(t)=Pwt(t)-Pwt(t-Δt)

(3)

2)時間段(t-Δt,t)內

ΔPwt(t)=max[Pwt(i)]-min[Pwt(i)]

(4)

3)引入t時刻的并網功率[12]

(5)

式中：i∈(t-Δt,t)；△Pwt(t)為爬坡幅值；△Pmax+(t)為t時刻與時間段(t-Δt,t)內的最小值之差；ΔPmax-(t)為t時刻與時間段(t-Δt,t)內的最大值之差。

式(3)、式(4)多用于靜態優化控制計算，而式(5)為動態定義，可有效避免遺漏越限情況。所研究的BESS運行情況，爬坡事件數值特征越接近實際越理想。

3 雙蓄電池組控制策略

t時刻風-儲系統的輸出功率波動幅值為

ΔPS(t)=ηwtΔPwt(t)-PB(t-Δt)+PB(t)

=ΔP(t)+PB(t)

(6)

式中：ηwt為風電系統效率(含損耗ΔPloss)；ΔP(t)為過渡變量。

BESS需要平抑的功率為ΔPB(t)。

(7)

式中,λ為安全裕度，保障電網安全。

蓄電池組儲能過程滿足：

(8)

式中：EB(t)為t時刻蓄電池組的剩余容量；ηch、ηdis為蓄電池組充、放電效率。

為了得到更好的平抑效果，對比同步與異步控制策略。

3.1 兩組蓄電池處于不同狀態

蓄電池組的最大充、放電功率為

(9)

式中:Pch(t)為蓄電池最大可充電功率；Pdis(t)為蓄電池最大可放電功率；PBmax為蓄電池額定功率(最大充放電爬坡率)；SOCmax為蓄電池最大荷電量；SOC(t)為蓄電池t時刻荷電狀態；EBESS為蓄電池額定容量。

假設BESS1為充電狀態，BESS2為放電狀態。

1)充電時，BESS2的狀態不變，PB2(t)=0；BESS1充電功率PB1ch(t)為

PB1ch(t)=-min{|ΔPB(t)|,|Pch(t)|}

(10)

2)放電時，BESS1的狀態不變，PB1(t)=0；BESS2的放電功率PB2dis(t)為

PB2dis(t)=min{|ΔPB(t)|,|Pdis(t)|}

(11)

同步控制時，BESS1或BESS2任意一組達到滿充或滿放狀態，下一刻BESS1和BESS2的狀態都改變。

異步控制時，任意一組BESS達到滿充或滿放狀態，下一時刻該組BESS改變狀態，另一組保持不變。

3.2 兩組蓄電池處于同一狀態

只在異步控制時發生。

1)都處于充電狀態：若|ΔPB(t)|可以被SOC(t-Δt)更接近SOCmax的蓄電池(假設為BESS1)全部吸收時，則根據式(10)計算；否則|△PB(t)|過大，兩個蓄電池組同時工作，BESS1充電電功率為PB1(t)，BESS2的充電功率為

(12)

PB(t)=PB1(t)+PB2(t)

(13)

2)都處于放電狀態：若|△PB(t)|可以被SOC(t-△t)更接近SOCmin的蓄電池(假設為BESS2)全部補足時，則根據式(11)計算；否則|△PB(t)|過大，兩個蓄電池組同時工作，BESS2放電功率為PB2(t)，BESS1的放電功率為

(14)

3.3 棄風與缺額

棄風發生在蓄電池充電狀態PB(t)<0:

(15)

缺額發生在蓄電池放電狀態PB(t)>0:

(16)

系統并網功率重新定義為

ΔPS(t)=ηwtΔPwt(t)+ΔPB(t)-ΔPcur(t)

=ΔP(t)+PB(t)-Pcur(t)

(17)

式中,ΔPwt(t)、ΔPB(t)、ΔPcur(t)分別為t時刻與(t-Δt)時刻的風電、蓄電池和棄風功率差。

4 優化模型

4.1 目標函數

1)儲能系統裝置費用Fequip

Fequip=wEEBESS+wpPBmax

(18)

式中：wE為BESS的單位容量費用；wP為BESS的單位功率費用。

2)蓄電池壽命費用Fcount

蓄電池的充放電次數有限，完整交替充放電記一次充放電次數[13]。

(19)

式中：nch、ndis分別為充、放電次數；ntotal為壽命周期；Minv為蓄電池投資成本。

3)棄風缺額懲罰費用Fpunish

(20)

式中,wcur、wlack分別為單位棄風和缺額費用。

4)總使用支出費用Fcost

(21)

式中，w1、w2為各目標函數所占的比例。

4.2 約束條件

蓄電池的充放電功率需滿足：

-PBmax≤PB(t)≤PBmax

(22)

為了避免過充過放，蓄電池組受到其荷電狀態的限制。

SOC(t)=EB(t)/EBESS

(23)

SOCmin≤SOC(t)≤SOCmax

(24)

4.3 評價指標

功率波動越限概率和幅值越小，平抑波動的效果越好，控制策略越有效。

1)波動越限次數U

(25)

(26)

式中,S為二進制數，取0或1。

2)波動越限概率ΔU

(27)

式中，T為總時間。

3)波動越限幅值之和ΔW

(28)

4.4 改進粒子群優化算法(IPSO)

為避免PSO陷入局部最優，引入慣性權重wk，較大的wk有利于提高收斂速度，較小的wk有利于提高收斂精度[14]。

(29)

式中：Dt為當前粒子的迭代次數；Dtmax為算法開始設置的最大迭代次數；wmax、wmin為設置的最大和最小慣性權重。

隨著迭代次數增加，希望粒子的搜索能力由局部尋優轉為全局尋優，因此，加速常數c1逐漸減小，c2逐漸增大[15]。

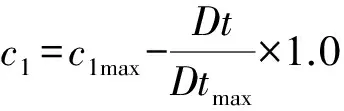
(30)

式中，c1max、c2min分別為最大和最小加速常數。

因此，粒子群速度和位置公式為

vDt+1=wkvDt+c1r1(pbest-pDt)+

c2r2(gbest-pDt)

(31)

pDt+1=pDt+vDt+1

(32)

式中：r1、r2為隨機數；pbest為單個粒子最優位置；gbest為全局粒子最優位置；pDt為粒子第Dt次迭代時的位置。

圖2 IPSO算法流程

5 算例分析

算例中的風電場額定功率為50 MW，選取該風電場某典型日的風電功率實測數據，采樣周期為1 min。風電功率10 min內輸出的波動不超過額定功率的10%，安全裕度取0.9。表1給出BESS的裝置參數和經濟系數。

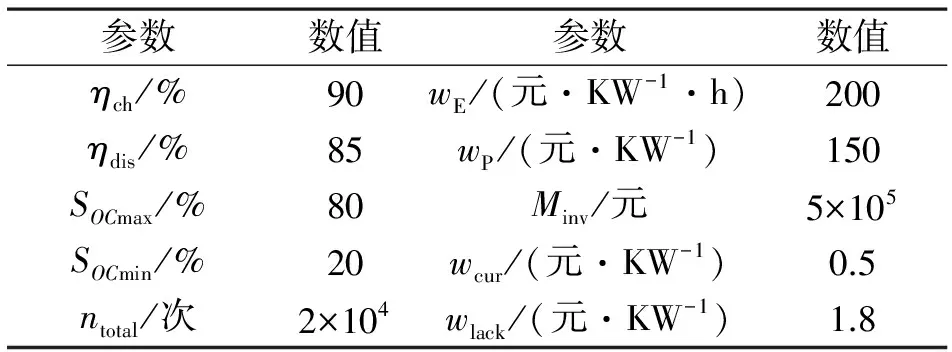
表1 BESS裝置參數和經濟系數

5.1 爬坡事件定義對比

分析不同定義下的風電爬坡事件。

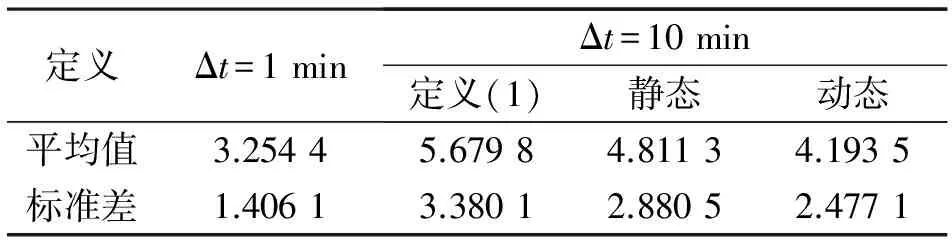
表2 風電爬坡事件數據特征

由表2可以看出，對比短時間的波動情況，可知動態定義下的數據平均值和標準差更能反映風功率的變化。

由圖3可以看出，動態定義能采集到更完整的波動情況，因此選擇動態定義進行研究更為合理。

蓄電池的充放電功率不僅受自身額定容量和功率的約束，而且受到并網條件的約束。因此，配置合適的蓄電池參數時需綜合考慮。

5.2 對比異步、同步控制策略

選取兩組額定容量均為10 MWh、額定功率均為5 MW的蓄電池，對比同步和異步控制策略的優劣性，見表3、表4。

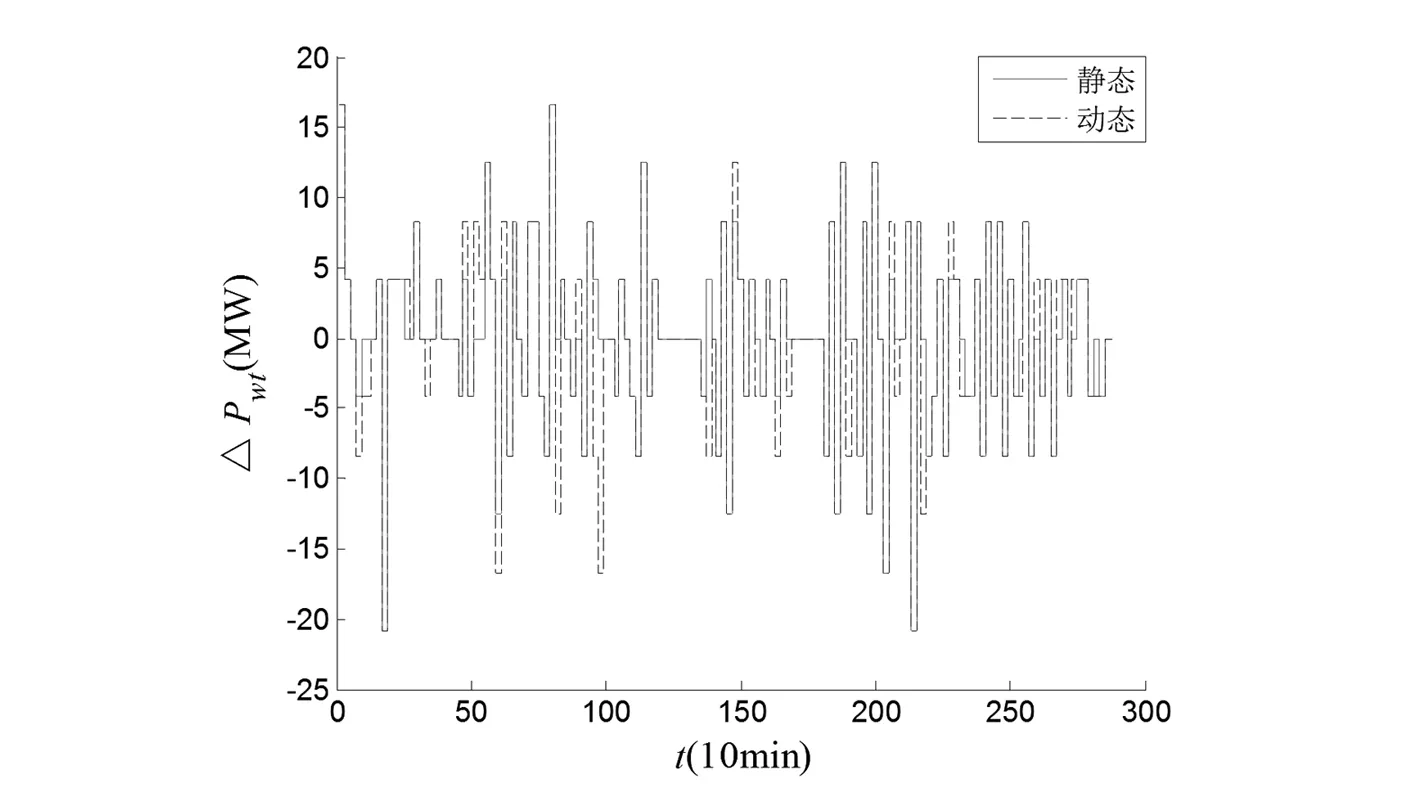
圖3 不同風電爬坡事件對比

表3 BESS平抑前的指標

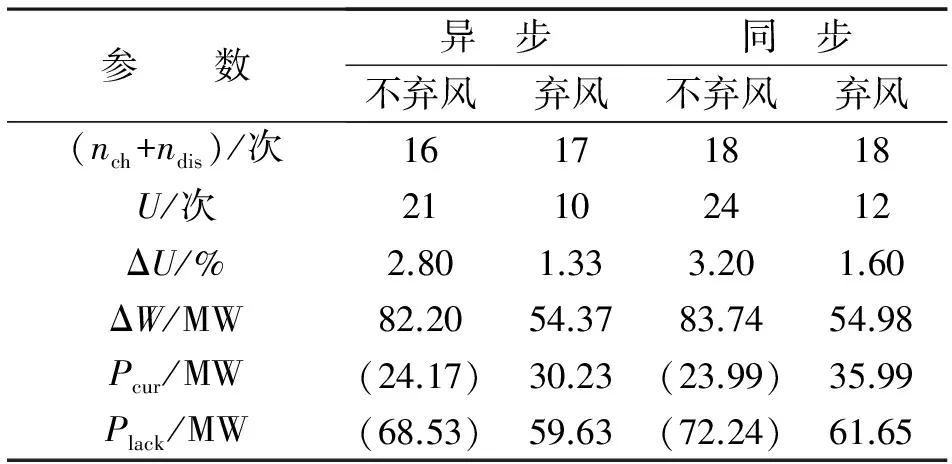
表4 異步與同步配置對比

由表3、表4可以看出，加入BESS后，波動越限概率和越限幅值大幅下降。舍棄多余的風電功率，明顯地改善了平抑效果。對比兩種控制策略下的指標可知，異步控制策略的波動越限概率及幅值都優于同步控制策略的。由分析可知，不同的額定容量和功率的BESS，容量和功率越大，輸出波動越小，平抑效果越好，但會增加額外的系統裝置費用。棄風和缺額總量與系統的額定功率及容量有關，綜合考慮裝置費用等因素，進行優化計算。

5.3 IPSO優化

IPSO中的各項參數：wmax=0.9，wmin=0.4，c1max=1.1，c2min=0.8。配置優化對比見表5，效果對比如圖4所示。

由表5可以看出，異步控制策略的BESS額定容量及額定功率要求相差不多，且其平抑效果更好，因此計及越限及棄風缺額懲罰費用，其總體費用比同步控制的小。

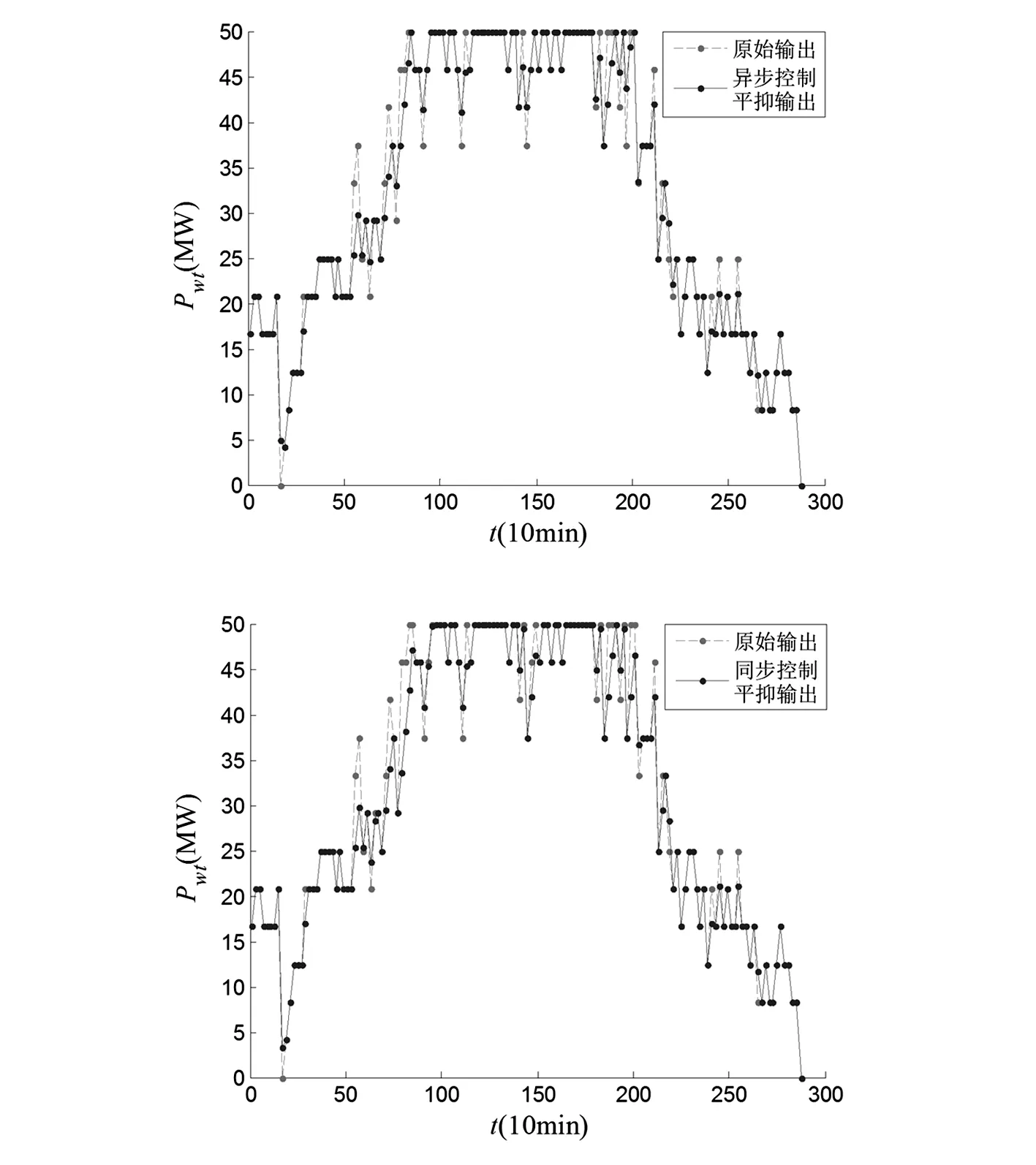
圖4 同步與異步控制的平抑效果對比

由圖4可以看出，在波動幅度較大時，異步控制更能充分利用蓄電池容量，最大限度利用風能，在不越限的情況下達到經濟最優化。

6 結 語

前面提出了一種基于抑制風電爬坡事件的優化配置雙蓄電池儲能并網系統參數的方法。首先分析了風電爬坡事件的不同定義的適用性，動態定義的風電爬坡事件更能體現實測數據的特征。詳細介紹了同步和異步控制策略，分析了兩種控制策略的優劣性，可知異步控制策略能有效地利用蓄電池容量，且平抑波動的效果更好，經濟性高。最后利用改進粒子群算法優化配置蓄電池組的參數。

[1] 汪海蛟, 江全元. 應用于平抑風電功率波動的儲能系統控制與配置綜述[J]. 電力系統自動化, 2014, 38(19): 126-135.

[2] 黎靜華, 左俊軍, 汪賽. 大規模風電并網電力系統運行風險評估與分析[J]. 電網技術, 2016, 40(11): 3503-3510.

[3] 邵麗華, 章竹耀, 張春龍, 等. 儲能電池荷電狀態與平抑風電出力波動協調運行策略[J]. 電力建設, 2017，38(1): 84-88.

[4] 婁素華, 吳耀武, 崔艷昭,等. 電池儲能平抑短期風電功率波動運行策略[J]. 電力系統自動化, 2014, 38(2): 17-22.

[5] Cong-Long Nguyen, Hong-Hee Lee. A Novel Dual-battery Energy Storage System for Wind Power Applications[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10)：6136-6147.

[6] 章竹耀, 郭曉麗, 張新松，等. 儲能電池平抑風功率波動策略[J]. 電力系統保護與控制, 2017, 45(3): 62-68.

[7] 何川, 劉天琪, 胡曉通, 等. 基于超短期風電預測和混合儲能的風電爬坡優化控制[J]. 電網技術, 2017, 41(3): 782-790.

[8] 吳雄, 王秀麗, 李駿,等. 風電儲能混合系統的聯合調度模型及求解[J]. 中國電機工程學報, 2013, 33(13): 10-17.

[9] 程世軍. 風電場儲能系統的優化配置及運行研究[D]. 北京：華北電力大學, 2014.

[10] 侯婷婷.含大規模風電的電力系統儲能電源優化配置研究[D]. 武漢: 華中科技大學, 2014.

[11] 謝應昭, 盧繼平, 翁宗林, 等. 改善風電輸出功率特性的復合儲能系統優化配置[J]. 電網技術, 2016, 40(7): 2052-2058.

[12] 王穎, 張凱鋒, 付嘉渝, 等. 抑制風電爬坡率的風儲聯合優化控制方法[J]. 電力系統自動化, 2013, 37(13): 17-23.

[13] Zhang X, Yuan Y, Hua L, et al. On Generation Schedule Tracking of Wind Farms with Battery Energy Storage Systems[J]. IEEE Transactions on Sustainable Energy, 2016, 8(1):341-353.

[14] 楊珺, 張建成, 黃磊磊,等. 基于改進粒子群算法的獨立光伏發電系統儲能容量優化配置研究[J]. 華東電力, 2012，40(8):1370-1374.

[15] Wang Yi, Jiang Hanhong, Xing Penxiang. Improved PSO-based energy management of Stand-alone Micro-grid under Two-time Scale[C]// IEEE International Conference on Mechatronics and Automation, 2016: 2128-2133.