基于服務質量的民航企業競爭決策分析

張驥驤+余曉磊

摘要：近年來廉價航空發展迅速，逐漸成為一種重要的旅游交通方式。廉價航空公司的迅速發展，使得傳統航空公司的地位受到了挑戰，民航市場的競爭也日趨激烈。一般情況下，傳統航空公司在服務質量上具有優勢，而廉價航空公司在票價上具有優勢。兩種航空公司各有不同的服務質量類別，在日趨激烈的市場情況下，兩種航空公司在面對競爭時也在不斷調整自己的服務策略，盡可能最大化自身的收益。本文以有限理性情況下的民航企業群體為研究對象，對民航企業群體中的傳統型航空公司和廉價航空公司的服務質量策略選擇進行分析，運用演化博弈方法研究民航企業服務質量策略選擇的動態演化過程，分析影響民航企業策略選擇的因素，探討演化結果，為民航企業制定服務質量策略提供理論建議。

Abstract： In recent years， low-cost aviation has developed rapidly and has gradually become an important tourist mode of transportation. The rapid development of low-cost airlines has challenged the status of traditional airlines and the competition in the civil aviation market has become increasingly fierce. In general， traditional airlines have an advantage in service quality， while low-cost airlines have an advantage over fares. Both airlines have different quality of service categories. In an increasingly fierce market， the two airlines are constantly adjusting their service strategies in the face of competition to maximize their own profits. This paper takes the civil aviation enterprise group under the limited rationality as the research object， analyzes the choice of the service quality strategy of the traditional airline and the low-cost airline in the civil aviation enterprise group， and uses the evolutionary game theory to study the dynamic evolution process of the service quality strategy choice of the civil aviation enterprise， analyze the factors influencing the choice of tactics of civil aviation enterprises， discuss the result of evolution， and provides theoretical suggestions for the civil service enterprises to formulate the strategy of service quality.

關鍵詞：航空公司；服務質量；有限理性；演化博弈；策略選擇

Key words： airlines；service quality；bounded rationality；evolutionary game；strategy choice

中圖分類號：F224.32；F560 文獻標識碼：A 文章編號：1006-4311（2018）08-0102-04

0 引言

隨著民航市場的迅速發展和變化，航空公司通過提供同質化產品和服務來獲得競爭優勢變得越來越困難。如今，航空公司面臨著諸多挑戰，如壓縮成本、管理效率低下、民航市場競爭加劇[1]。此外，日益激烈的市場競爭也使得消費者對服務質量的滿意度變得日益重要。由于我國民航運輸業起步較晚，在航空運輸的產品設計、品牌建設、客戶管理等與服務質量相關的方面，航空公司仍有很大的提升空間[2-3]。而隨著我國經濟實力和人民物質水平的不斷提高，對航空運輸服務質量有著越來越高要求的商務旅客的數量也在飛速增長。這類旅客對航空運輸服務質量的要求是全方位的，而不再僅僅是從甲地到乙地的運輸那么簡單。這些要求既包括機型、飛機客艙設備、地面服務環境等硬件要求，也包括對服務人員態度、服務的方便性等軟件方面的要求[4-5]。但服務質量的提高也意味著航空公司運營成本的提高，航空公司在與競爭對手進行服務策略博弈時，如何在保證旅客滿意的情況下同時保證航空公司的盈利和競爭力，對航空公司而言是一個至關重要的命題[6]。因此對航空公司價格和服務的博弈研究有助于航空公司制定差異化的經營策略，對民用航空業的發展有著重要的意義。

縱觀當前研究文獻，對航空公司競爭博弈的研究尚有如下幾點不足：一是不同的競爭策略對航空公司的競爭行為有很大的影響，大多數文獻只研究了相同競爭策略下的航空公司的博弈；二是絕大多數文獻假設航空公司在決策過程中是完全理性的，而這明顯不符合實際情況；三是目前研究航空公司競爭博弈的文獻多數都是定性分析，缺乏對航空公司間服務質量競爭的定量與數理分析。endprint

因此，本文基于有限理性博弈理論，運用演化博弈方法研究民航企業群體服務質量策略選擇的動態演化過程，分析影響民航企業策略選擇的因素，探討演化結果，為民航企業制定服務質量策略提供理論建議。

1 模型的建立

考慮到一個航空市場上存在眾多參與競爭的航空公司，主要分為廉價航空公司和傳統型航空公司。各航空公司都是有限理性的，他們在博弈過程中通過學習和模仿不斷調整自己的策略以實現自身利益最大化。現有如下假設：

①兩種航空公司的原始收益是∏1、∏2，∏1>0，∏2>0。

②廉價航空公司可以選擇提高服務質量或維持低成本服務，傳統型可以選擇降低服務質量或維持高質量服務。設f1，f2分別為兩種航空公司的服務質量，當廉價航空公司提高服務質量后，此時的服務質量為f =（1+δ）f1；當傳統型航空公司降低服務質量時，此時的服務質量為f =（1-θ）f2，其中0<δ，0<θ<1。

③當廉價航空公司提高服務質量時，需要付出額外成本，設該成本為C1=εδ2f ；當傳統型航空公司降低服務質量時，可以節省一定的成本，設該成本為C2=ωθ2f 。其中ε，ω為成本系數，一般情況下，ε>0，ω>0，ω>ε。

④服務質量會影響乘客的滿意度，進而影響航空公司的口碑。由于廉價航空公司的票價低，乘客對其服務質量預期低。相反，由于傳統型航空公司較高的票價，乘客對其服務質量有著較高的預期。假設口碑也是一種收益，當廉價航空公司提高服務質量，而傳統型航空公司降低服務質量時，此時廉價航空公司獲得的口碑為S1=A（δ2f +θ2f ），而傳統型航空公司則失去口碑S1；當廉價航空公司提高服務質量，傳統型航空公司維持高質量服務時，此時廉價航空公司獲得的口碑為S2=Aδ2f ；當廉價航空公司維持低質量服務，傳統型航空公司降低服務質量時，此時傳統型航空公司失去的口碑S3=Aθ2f 。其中，A為與服務質量相關的口碑系數，A>0。

根據以上假設，建立廉價型航空公司和傳統型航空公司在這兩種策略下的博弈收益矩陣，如表1所示。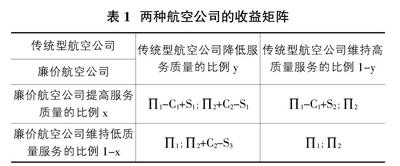

2 模型的演化博弈分析

2.1 演化過程的平衡點

假設在廉價航空公司群體中，選擇提供高質量服務的比例為x（x∈[0，1]），則選擇維持低成本服務的比例為1-x；而在傳統型航空公司群體中，選擇降低服務質量的比例為y（y∈[0，1]），則選擇維持高成本服務的比例為1-y。

根據表1所示的收益矩陣，廉價型航空公司選擇“提高服務質量”和“維持低成本服務”策略的期望效用為μ11，μ12，而該群體的平均效用為 ，則可得：

μ11=y（∏1-C1+S1）+（1-y）（∏1-C1+S2）

μ12=y∏1+（1-y）∏1

=xμ11+（1-x）μ12

同理，傳統型航空公司選擇“降低服務質量”和“維持高成本服務”策略的期望效用為μ21，μ22，平均效用為 ，可得：

μ21=x（∏2+C2-S1）+（1-x）（∏2+C1-S3）

μ22=x∏2+（1-x）∏2

=yμ21+（1-y）μ22

根據復制動態的復制動態公式，廉價航空公司選擇“提高服務質量”策略的數量增長率等于其期望效用減去平均效用，t為時間，可得廉價航空公司和傳統型航空公司“降低服務質量”策略的復制動態方程

=x（1-x）[（A-ε）δ2f +yAθ2f ] =y（1-y）[（ω-A）θ2f -xAδ2f ]

可以求得點（0，0），（0，1），（1，0），（1，1）是該系統的平衡點。

當ω>A，ε>A，（ω-A）θ2f

0

2.2 平衡點的穩定性分析

進化穩定策略點（ESS）是動態進化過程中的局部漸進穩定不動點，對微小的擾動具有穩定性，因此，由動態復制方程求出的平衡點不一定是ESS，判斷平衡點的穩定性需要通過動態復制方程的雅克比（Jacobian）矩陣的局部穩定性來分析。

由矩陣Jacobian的行列式det（J）和跡tr（J）來判定Jacobian矩陣的局部穩定性，即若det（J）>0且tr（J）<0，則對應的平衡點是ESS；若det（J）>0且tr（J）>0，則對應的平衡點為不穩定點；若det（J）<0，則對應的平衡點為鞍點。各平衡點的行列式和跡如表2所示。

根據表2的結果和判定Jacobian矩陣的局部穩定性方法，對平衡點穩定性分情況進行討論。

①當ε>A>ω，（A-ε）δ2f +Aθ2f <0且εδ2f -ωθ2f >0時，（0，0）為ESS，（0，1）為鞍點，（1，0）為鞍點，（1，1）為不穩定點。

②當ε>A>ω，（A-ε）δ2f +Aθ2f <0，且εδ2f -ωθ2f <0時，（0，0）為ESS，（0，1）為鞍點，（1，0）為鞍點，（1，1）為ESS。

③當A>ω>ε時，（0，0）為鞍點，（0，1）為不穩定點，（1，0）為ESS，（1，1）為鞍點。

④當ω>A>ε，（ω-A）θ2f

⑤當ω>ε>A，（A-ε）δ2f +Aθ2f <0，（A-ε）δ2f +（2A-ω）θ2f <0，（ω-A）θ2f >Aδ2f 時，（0，0）為鞍點，（0，1）為ESS，（1，0）為不穩定點，（1，1）為鞍點。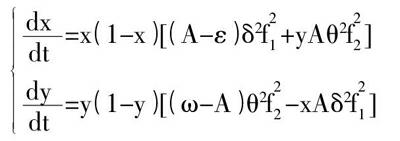

⑥當ω>ε>A，（A-ε）δ2f +Aθ2f <0，（A-ε）δ2f +（2A-ω）θ2f <0，（ω-A）θ2f

⑦當ω>ε>A，（A-ε）δ2f +Aθ2f >0，（A-ε）δ2f +（2A-ω）θ2f >0，（ω-A）θ2f >Aδ2f 時，（0，0）為鞍點，（0，1）為鞍點，（1，0）為不穩定點，（1，1）為ESS。

⑧當ω>ε>A，（A-ε）δ2f +Aθ2f >0，（A-ε）δ2f +（2A-ω）θ2f >0，（ω-A）θ2f

⑨當ω>ε>A，（A-ε）δ2f +Aθ2f <0，（A-ε）δ2f +（2A-ω）θ2f >0，（ω-A）θ2f >Aδ2f 時，（0，0）為鞍點，（0，1）為不穩定點，（1，0）為不穩定點，（1，1）為鞍點。

⑩當ω>A>ε，（ω-A）θ2f >Aδ2f 且εδ2f <ωθ2f 時，（0，0）為不穩定點，（0，1）為鞍點，（1，0）為鞍點，（1，1）為ESS。

{11}當ω>A>ε，（ω-A）θ2f >Aδ2f 且εδ2f >ωθ2f 時，（0，0）為不穩定點，（0，1）為鞍點，（1，0）為鞍點，（1，1）為不穩定點。

2.3 演化結果分析

情況①②分析：當廉價航空公司的成本系數較大，傳統型航空公司成本系數較小時，若廉價航空公司提高服務質量后所帶來的口碑收益要小于所付出的額外成本，且兩家航空公司服務質量調整幅度不大時，此時廉價航空公司會選擇維持較低質量的服務，而傳統型航空公司會選擇維持較高質量的服務，因此（0，0）是進化穩定點。若兩家航空公司的服務質量調整幅度極大，即傳統型航空公司大幅度降低服務質量，廉價航空公司大幅度提升服務質量，這種情況近似于傳統型航空公司提供低質量服務，廉價航空公司提供高質量服務，兩家航空公司“身份互換”，此時（1，1）也是進化穩定點。情況①②的系統相位圖如圖1、圖2所示。

情況③④分析：當額外收益系數A較大，而兩家航空公司的成本系數ω和δ較小時，即廉價航空公司提高服務質量后，所獲得的額外口碑收益遠大于付出的額外成本；而傳統型航空公司若降低服務質量，所遭受的口碑收益損失遠超過降低服務質量后節省的成本。這時廉價航空公司顯然會選擇提高服務質量，而傳統型航空公司會選擇維持較高質量的服務，因此（1，0）點是進化穩定點。情況③④的系統相位圖如圖3所示。

情況⑤⑥分析：當兩家航空公司的成本系數較大，而額外收益系數較小時，即廉價航空公司提高服務質量后，所獲得的額外口碑遠小于付出的額外成本；而傳統型航空公司若降低服務質量，所節省的成本遠超過降低服務質量后所帶來的口碑收益損失。這時廉價航空公司顯然會選擇維持較低質量的服務，而傳統型航空公司會選擇降低服務服務質量來節省成本，因此（0，1）是進化穩定點。情況⑤⑥的系統相位圖如4所示。

情況⑦⑩分析：當航空公司額外收益系數較小，而成本系數ω和δ較大時，此時傳統型航空公司降低服務質量所節省的成本遠高于失去的口碑收益，因此傳統型航空公司會選擇降低服務質量。而對于廉價航空公司，雖然提高服務質量會導致成本大幅度升高，但傳統型航空公司所喪失的口碑收益與廉價航空公司的口碑收益之和要大于廉價航空公司所付出的成本，這意味著廉價航空公司將收獲更多的客源，此收益高于付出的成本，所以廉價航空公司會選擇提高服務質量。因此（1，1）是進化穩定點。情況⑦⑩的系統相位圖如圖5所示。

3 結論

本章通過演化博弈法對民航企業關于服務質量的決策行為進行了分析，研究了傳統航空公司和廉價航空公司之間的服務質量策略博弈。分析結果表明，航空公司的服務質量策略選擇的關鍵在于提高（降低）服務質量后所增加（降低）的成本與增加（降低）的額外口碑收益。

若兩種類型的航空公司成本系數偏大而額外收益系數偏小時，即廉價航空公司提高服務質量所獲得額外口碑收益遠小于付出的成本，傳統型航空公司降低服務質量所節省的成本遠高于損失的口碑收益，這時廉價航空公司將趨向于維持低質量服務，而傳統型航空公司則趨向于降低服務質量來節省成本，所以此時民航市場中的航空服務水平普遍偏低。若航空公司成本系數偏小而額外收益系數偏大時，則結果相反，廉價航空公司趨向提高服務質量而獲得更大的額外口碑收益，傳統型航空公司則趨向于維持高質量服務，則此時民航市場中的平均服務水平較高。若廉價航空公司的成本系數較大，傳統型航空公司成本系數較小時，且兩家航空公司服務質量調整幅度不大時，此時廉價航空公司會選擇維持較低質量的服務，而傳統型航空公司會選擇維持較高質量的服務。若兩家航空公司的服務質量調整幅度極大，即傳統型航空公司大幅度降低服務質量，廉價航空公司大幅度提升服務質量，這種情況近似于傳統型航空公司提供低質量服務，廉價航空公司提供高質量服務，兩家航空公司“身份互換”。民航市場最理想的狀態是在航空公司保證自身盈利的同時，為旅客提供高質量高水平的民航運輸服務，這不但要求航空公司進行高效的成本控制和收益管理，還要求民航市場上有足夠多對高水平服務質量有需求的旅客數量。

而隨著民航市場的日漸成熟和經濟水平的日益繁榮，高端消費者所占的比例也逐步增加，旅客對航空公司的軟硬件設備、機艙服務，以及服務的可靠性與關懷性要求越來越高時，航空公司提高服務質量后能為自身帶來更多的回頭客和口碑收益，即較高的額外收益。雖然航空公司提高服務質量后，不可避免地會帶來自身成本的增高，但有些服務項目質量的提升與改善，其實所費無幾，例如機艙舒適清潔度、餐飲服務的安排、免稅品銷售的適時性、服務人員聆聽乘客談話的專心度等等，廉價航空公司可以優先考慮改善這些服務項目的質量。而對于傳統航空公司，除了模仿廉價航空公司降低可控成本，提供收費性服務，還可以發揮自身優勢，堅持走高端路線，在降低自身可控成本、提升收益管理效率的情況下，針對旅客的服務需求設計服務標準，注重服務細節。這樣使得廉價航空公司和傳統航空公司都能針對自身的經營策略發揮自身的優勢，避免了航空公司間的價格戰，使得航空公司在滿足自身盈利需求的情況下，也使得對民用航空運輸服務要求較低和較高的旅客需求都能得到滿足，從而促進民航市場健康發展。

參考文獻：

[1]沙永全.航空公司服務質量問題的成因分析[J].世界標準化與質量管理，2005（7）：35-36.

[2]王偉華，左洪福.基于不確定信息的航空公司服務質量評估.[J]人類工效學，2007（03）：23-24.

[3]吳暉，航空公司服務質量旅客滿意度研究.[J]現代商業，2008（10）：175-176.

[4]趙鳳彩，吳婧.國內外航空公司服務質量的對比分析.[J]中國民用航空，2009（09）：57-59.

[5]陳嘉賢，王姍媚，李潔，劉菲，林威，從服務質量及機票價格比較傳統和廉價航空的優勢——以澳門國家機場為例.[J]旅游學刊，2009（24）：87-91.

[6]魚文英，李京勛.航空服務質量概念模型與實證分析.[J]北京航空航天大學學報，2011（24）：79-82.