基于PCA算法的機載LiDAR點云平面分割算法研究

葉玲潔，顏遠青

(1.廣州市城市規(guī)劃勘測設(shè)計研究院，廣東 廣州 510060； 2.珠海大橫琴科技發(fā)展有限公司，廣東 珠海 519000)

1 引 言

在建筑物的三維重建中，屋頂面提取是其中最關(guān)鍵的部分[1]，后續(xù)工作都在屋頂面準確提取的基礎(chǔ)上進行。按照屋頂面的平整度，可以將屋頂面分為平面式屋頂和曲面式屋頂，現(xiàn)代建筑中尤其是城市建筑物，一般都較為規(guī)則，屋頂面多為平面式，而對于曲面式屋頂，難以直接用參數(shù)定義其曲面形狀，常規(guī)的做法是對其構(gòu)建Delaunay三角網(wǎng)，以三角面片的形式來擬合曲面。本文的研究重點主要是針對平面式屋頂面，因此對曲面式的屋頂面不進行研究討論。

在屋頂面分割算法中，目前常用的主要是RANSAC(Random Sample Consensus，隨機抽樣一致性)算法[2]、區(qū)域增長算法[3]、三維霍夫變換算法[4]、聚類算法等。區(qū)域增長算法首先選定一個種子區(qū)域，根據(jù)屋頂面點云與種子區(qū)域的法向量夾角、空間位置關(guān)系不斷地拓展面片，該方法分割效果良好，但是算法中參數(shù)選取較為困難，同時由于法向量的計算易受噪聲點影響，進而使得算法增長出錯誤的平面。RANSAC是一種隨機參數(shù)估計算法，首先從點云中隨機選取三個點，計算出平面參數(shù)，然后計算其他點與該平面的偏差，當偏差小于閾值，則該點為局內(nèi)點，不斷迭代找到局內(nèi)點最多的平面，則為最優(yōu)平面模型。RANSAC能魯棒的估計模型參數(shù)，但是其迭代次數(shù)必須足夠多才能得到準確的結(jié)果，效率低下。

在進行平面擬合時，常用的方法是最小二乘法進行平面擬合，但最小二乘法對于自變量與因變量無法區(qū)分的情況，適應(yīng)性差[5]，在實際中，一般認為接近垂直于地面的屋頂面是不存在的，以Z坐標作為因變量來對屋頂面進行最小二乘擬合平面。同時，在屋頂面點云存在噪聲點的情況下，對擬合結(jié)果影響很大。

本文利用PCA(Principal Component Analysis，主成分分析法)來計算點云的法向量，并以區(qū)域增長法來對平面進行分割。PCA算法可以有效減小噪聲點對法向量計算的影響，改善區(qū)域增長的結(jié)果。

2 平面擬合

本文中采用PCA的方法對點云進行平面擬合。PCA是一種數(shù)學(xué)變換的方法，利用降維的思想在變換中保持變量的總方差不變，將給定的一組變量線性變換為另一組不相關(guān)的變量，并且使變換后的第一變量的方差最大，即第一主成分，其他分量的方差依次遞減[6]。在本文中的變量為三維點坐標的集合，其變量為X、Y、Z三個坐標值，則經(jīng)過變換后，應(yīng)有三個主成分，對于一個空間平面，在平行于平面的方向上點集分布最為離散，方差最大，在垂直于平面的方向上，點集分布最為集中，方差最小，即空間平面的第三主成分為垂直于空間平面的向量。由于平面擬合最關(guān)鍵的為法向量的擬合，利用PCA得到點集的第三主成分，即能進一步擬合出平面方程，如圖1所示。

圖1 PCA變換原理

對于在坐標系XYZ下的待擬合平面點云，利用主成分分析法對其進行分析，可得到三個按照從大到小排列的特征值λ1、λ2、λ3，對應(yīng)的主分量分別為V1、V2、V3，其中V1和V2組成了待擬合平面的一組基，V3與V1、V2正交，為垂直于待擬合平面的法向量。如圖1，在XYZ坐標系下的點云，經(jīng)過主成分分析后，三個主成分分量V1、V2、V3組成了新坐標系X′Y′Z′的三個基，V1和V2為平面X′O′Z′的一組基，V3為O′Z′方向的基，即所擬合平面的法向量。

PCA過程如下：

(1)特征中心化。即每一維的數(shù)據(jù)都減去該維的均值，變換之后每一維的均值都變成了零。特征中心化后的點集P，如式(1)，其中，xi、yi、zi為中心化后點坐標：

(1)

(2)計算三個坐標的協(xié)方差矩陣。協(xié)方差矩陣C為：

(2)

其中，cov(x，y)為x坐標和y坐標的協(xié)方差，cov(x，x)為x坐標的方差，協(xié)方差計算公式如式(3)，xi、yi為中心化后點坐標：

(3)

當協(xié)方差大于零時說明x和y是正相關(guān)關(guān)系，協(xié)方差小于零時x和y是負相關(guān)關(guān)系，協(xié)方差為零時x和y相互獨立。

(3)計算協(xié)方差矩陣C的特征值和特征向量。所計算出來的特征值按照從大到小排序，分別為λ1、λ2、λ3，其所對應(yīng)的特征向量分別為ξ1、ξ2、ξ3。顯然，兩個較大λ所對應(yīng)的特征向量ξ1、ξ2為待擬合平面的一組基，而ξ3為待擬合平面的法向量，其三個分量分別為a、b、c。

若已知待擬合平面經(jīng)過點p(x0，y0，z0)p(x0，y0，z0)，則擬合平面為式(4)：

a(x-x0)+b(y-y0)+c(z-z0)=0

(4)

采用主成分分析法擬合平面的方法，對于存在噪聲點的情況，也能很好的擬合出結(jié)果。因為在一個平面點云中，噪聲點偏離平面的距離相對于平面的范圍較小，對擬合結(jié)果的影響可以忽略。

3 法向量計算

傳統(tǒng)的平面分割算法中，對于點的法向量計算通常是采用以點為圓心，r為半徑的一個鄰域，取鄰域內(nèi)的所有點云進行最小二乘擬合，這種方法在平滑變化的曲面上，計算的結(jié)果不會有太大偏差，但是在邊緣處，法向量難以確定，其結(jié)果是不準確的[7]。

本文中，首先對點的法向量進行計算。在選擇點云的鄰域點時，把當前表面情況考慮進去，即對于在同一個平面上，且空間上相鄰近，則認為是鄰域點，若不在同一個平面上，即使空間上相鄰近，也不視為鄰域點[8]。

圖2 初始鄰域點的選擇

法向量計算的主要步驟如下：

(1)定義所求點的r鄰域，搜索到其所有鄰域點，并進行平面擬合，擬合結(jié)果為Φinit。其中，如圖2，初始的鄰域點為在以所求點為球心，r為半徑的區(qū)域內(nèi)的所有點，都認為是所求點的鄰域點；

(2)計算鄰域點到Φinit的距離di的中誤差σ，將距離di小于兩倍中誤差的點權(quán)值設(shè)為1，距離di大于兩倍中誤差的點權(quán)值設(shè)為0。重新擬合平面Φinit；權(quán)值計算公式如(5)：

(5)

(3)多次擬合，直到所擬合的平面參數(shù)不再改變或者改變量小于閾值，此時擬合的平面為Φi。則Φi的法向量為所求點的法向量。

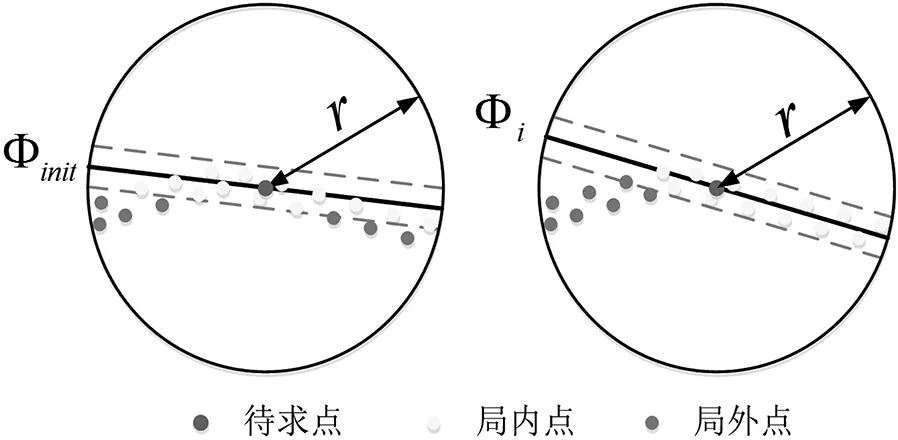
圖3 法向量求解過程

法向量的求解過程，也就是所求點處平面的擬合過程，可以用圖3表示，初始擬合的平面采用了r鄰域內(nèi)的所有點云進行擬合，其結(jié)果為Φinit，鄰域內(nèi)與Φinit的距離小于2σ的權(quán)值為1，如圖中黃色點，將權(quán)值為1的點重新擬合，多次擬合，最終結(jié)果為Φi，從圖3中可看出，此時所采用的用來擬合Φi的鄰域點為待求點的r鄰域內(nèi)，且在同一個平面內(nèi)的點。如圖4，將以待求點為球心，r為半徑的區(qū)域內(nèi)，與待求點在同一個平面內(nèi)的點，作為待求點的鄰域點，以最終確定的鄰域點來計算所求點的法向量。

圖4 最后鄰域點的確定

4 平面分割

本文中平面分割的主要算法為區(qū)域增長，主要步驟如下[9]：

(1)生成分割結(jié)果列表L，種子點隊列S，當前區(qū)域點列表Q；

(2)計算所有點的法向量和曲率。點pi對應(yīng)的法向量、曲率分別為ni、ci；

(3)選擇曲率最小且未聚類點作為種子點，將其添加到種子點隊列S和當前平面點列表Q中；

④若種子點隊列S為空時，當前平面提取完成，將當前平面點列表Q保存到分割結(jié)果列表L中；重置Q。

(5)最后的分割結(jié)果保存在列表L中。

在將點云數(shù)據(jù)進行平面分割后，同一個平面上的點云將被劃分到同一個聚類中。此時，對其進行平面擬合，計算出平面參數(shù)。做法是采用PCA算法計算得到平面的法向量，即平面參數(shù)a、b、c，將點集內(nèi)所有點求其中心，以其中心作為平面上點，計算出平面參數(shù)d。

5 實驗與分析

圖5 人字形屋頂面的區(qū)域增長算法分割結(jié)果

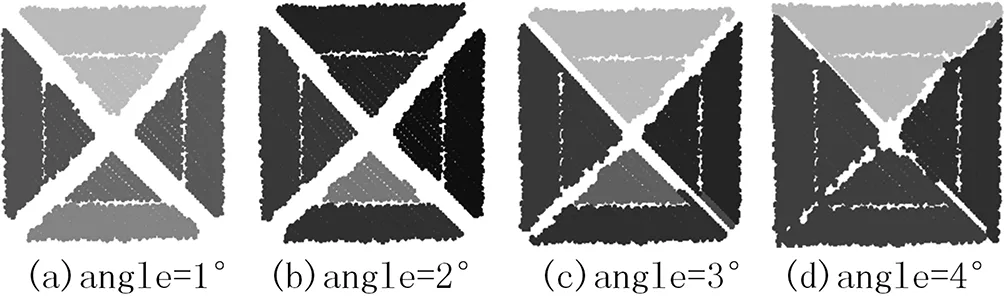
圖6 錐形屋頂面的區(qū)域增長算法分割結(jié)果

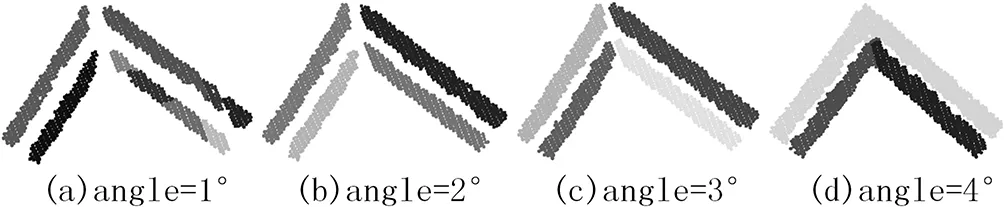
圖7 L形屋頂面的區(qū)域增長算法分割結(jié)果

圖5、圖6、圖7，為三組不同數(shù)據(jù)，采用傳統(tǒng)的區(qū)域增長對數(shù)據(jù)進行平面分割的結(jié)果，其中，angle為角度閾值，可以看出，在平面上無噪聲或者噪聲較少的情況下，區(qū)域增長算法提取出來的平面內(nèi)部點較為連續(xù)，不會出現(xiàn)空洞，但在邊緣處的點云無法很好地分割開。這是因為邊緣處的點云法向量計算困難，無法得到其正確的法向量，因此邊緣處的點云分割較為零碎，而本文中設(shè)定，當點數(shù)少于閾值時，不判別為一個平面，即一個平面上，必須有足夠多的點，才能被識別出。本文設(shè)置閾值為20個點。同時，區(qū)域增長的參數(shù)不容易設(shè)置，對于不同形狀的點云需要不同的參數(shù)，使得建筑物平面點云自動化分割難以實現(xiàn)，制約了建筑物自動化三維重建的可能。

圖8 錐形屋頂面的RANSAC算法分割結(jié)果

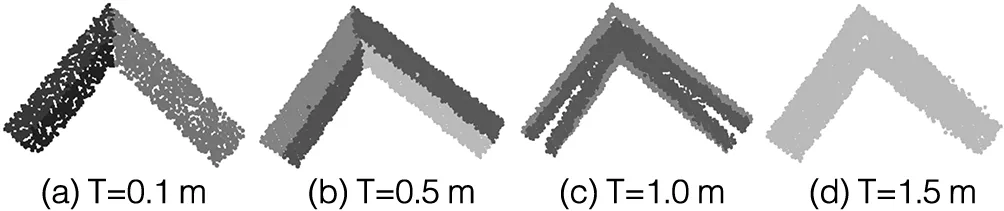
圖9 L形屋頂面的RANSAC算法分割結(jié)果

圖8、圖9，為兩組數(shù)據(jù)，采用了RANSAC算法對數(shù)據(jù)進行平面分割的結(jié)果，其中，T為閾值。可以看出，RANSAC在參數(shù)合適的時候能夠較好地分割出平面。但是，RANSAC提取出的每個平面并不是等價的，第一個被提取出的平面總是會擁有更多的點，這一點在圖8的T=1.0 m時表現(xiàn)比較明顯。此外，參數(shù)不合適時，出現(xiàn)各種錯誤情況，如T=0.1 m時，平面中出現(xiàn)很多空洞，這是由于機載LiDAR掃描的點云在高程方向有一定的波動，但被RANSAC錯誤地濾掉；在第一組T=1.5 m和第二組T=1.0 m時，則出現(xiàn)全局最優(yōu)，RANSAC只把全局內(nèi)，分配到當前平面點數(shù)最多的判別為平面。

圖10本文算法結(jié)果與影像對比

圖10為本文算法分割結(jié)果與實際影像對比，可以看出分割的結(jié)果較為準確，在平面相交的邊緣處也沒有因為點云法向的不確定性而導(dǎo)致的錯誤分割或者邊緣缺失的情況。

而對于圖11類型的穹頂建筑，本文算法無法適應(yīng)。

圖11 穹頂屋頂建筑

6 結(jié) 語

本文簡單介紹了常用的平面分割算法，包括三維霍夫變換、RANSAC算法和區(qū)域增長算法。三維霍夫變換需要將點云變換到屬性空間，計算量較大，一般較少使用；RANSAC算法需多次迭代，效率低下，在參數(shù)不合適的時候，也容易出現(xiàn)全局最優(yōu)而導(dǎo)致分割錯誤，此外，若第一個提取的平面擁有更多的點也導(dǎo)致后續(xù)提取的平面質(zhì)量不斷下降；區(qū)域增長算法對邊緣處的法向量計算比較困難，隨之出現(xiàn)的是邊緣處的點云無法很好地分割到平面上。

本文采用PCA算法擬合局部平面的方法，并根據(jù)點到平面的距離設(shè)置權(quán)值，迭代多次后得到最準確的平面及其所對應(yīng)的法向量，由于所選擇的鄰域一般較小，所迭代次數(shù)相對于RANSAC算法大大減少。但在屋頂面點云數(shù)量較少的情況下，噪聲點對屋頂面法向量計算影響變大，容易導(dǎo)致法向量計算出錯，從而使得分割結(jié)果錯誤。計算出法向量后，再以區(qū)域增長算法來對點云數(shù)據(jù)進行分割，經(jīng)過實驗，其結(jié)果準確，分割效果良好。根據(jù)本文算法進行點云平面分割，其結(jié)果可應(yīng)用于建筑物的建模、點云分類等。本文算法主要針對平面點云的分割，對于平頂、坡頂甚至多平面復(fù)合型建筑物屋頂點云分割效果較好，但對于穹頂、曲面建筑物屋頂點云無法適用，筆者將繼續(xù)深入研究并加以改進。

[1] 胡偉，盧小平，李珵等. 基于改進RANSAC算法的屋頂激光點云面片分割方法[J]. 測繪通報，2012(11)：31～34.

[2] 李娜，馬一薇，楊洋等. 利用RANSAC算法對建筑物立面進行點云分割[J]. 測繪科學(xué)，2011，36(5)：144～145.

[3] 李寶順，岑紅燕，包亞萍等. 基于平面提取的點云數(shù)據(jù)分割算法[J]. 計算機應(yīng)用與軟件，2014，31(7)：145～148.

[4] 黃先鋒. 利用機載LIDAR數(shù)據(jù)重建3D建筑物模型的關(guān)鍵技術(shù)研究[D]. 武漢：武漢大學(xué)，2006.

[5] 浮丹丹，周紹光，徐洋等. 基于主成分分析的點云平面擬合技術(shù)研究[J]. 測繪工程，2014，23(4)：20～23.

[6] 王松，夏紹瑋. 一種魯棒主成分分析(PCA)算法[J]. 系統(tǒng)工程理論與實踐，1998(1)：10～14.

[7] 楊斌. 機載LiDAR點元數(shù)據(jù)建筑物半自動提取方法研究[D]. 阜新：遼寧工程技術(shù)大學(xué)，2012.

[8] Kim C，Habib A，Pyeon M，et al. Segmentation of Planar Surfaces from Laser Scanning Data Using the Magnitude of Normal Position Vector for Adaptive Neighborhoods[J]. Sensors，2016，16(2)：140.

[9] 楊洋，張永生，張皓等. 基于LiDAR數(shù)據(jù)的建筑物自動化重建[J]. 測繪科學(xué)技術(shù)學(xué)報，2010，27(2)：123～126.

[10] 姜如波. 基于三維激光掃描技術(shù)的建筑物模型重建[J]. 城市勘測，2013，3：113～116.