巖石薄片正交偏光序列圖像的顆粒分割
李周,滕奇志*,張余強
(1.四川大學電子信息學院圖像信息研究所,成都610065;2.成都西圖科技公司,成都 610024)
0 引言
在石油地質行業中,確定巖石中各礦物成分比例是薄片礦物鑒定的重要內容[1],對巖石顆粒進行準確分割則是確定礦物成分的前提。在巖石薄片圖像中,顆粒表面紋理復雜,形狀各異,顆粒間差異不明顯,導致巖石顆粒圖像自動分割的難度較大。
不少學者對巖石顆粒圖像的自動分割進行了研究,如文獻[2]中B.Obara將巖石圖像轉換到不同的顏色空間,然后再進行閾值分割。文獻[3]中Gorsevski等使用了基于元胞自動機演化的邊緣檢測方法對巖石圖像進行分割。雖然已有較多的顆粒分割算法研究,但是能夠實際應用的卻比較少。因為在自動分割之后,仍需要進行大量的人工交互,對巖石顆粒的分割結果進行修正,自動化程度不高。
文獻[4]中提到,巖石樣品中晶體存在消光特性,在不同正交偏光角度下,顆粒的亮度會發生變化,顆粒之間的邊界也能清晰地顯示出來,所以可以利用這種特性來輔助巖石顆粒的分割。以此為依據,本文通過對采集到的不同正交偏光角度下的巖石薄片序列圖的分析處理,最終實現顆粒的自動分割。
1 偏光序列圖采集處理
采集巖石薄片圖像一般是通過在顯微鏡下利用投射單偏光來獲取圖像,但是由于單偏光下巖石薄片圖像中的顆粒缺乏清晰的輪廓,顆粒之間沒有良好的區分度,如圖 1(a)所示。
本文使用正交偏光系統下采集的序列圖進行圖像分割。正交偏光系統是在單偏光系統的基礎上再加上一個單偏光鏡,上、下偏光鏡振動方向相互垂直,將巖石薄片放在上、下偏光鏡之間的載物臺上,視域中將呈現一系列光學現象,如消光、干涉色等[6]。采用自主研制的偏光圖像采集裝置,每旋轉正交偏光鏡15°獲取一幅圖像,總共旋轉120°,一共采集9張序列圖像。圖1(b)(c)(d)為其中 0°,60°,90°角度的 3 張圖像,可以看出,正交偏光圖像中的巖石顆粒清晰,但是由于顆粒的消光現象,在單張正交偏光圖中并不能把所有顆粒都顯示出來。
2 顆粒分割

圖1 單偏光圖像和不同角度下的正交偏光圖像
利用一組正交偏光序列圖像進行顆粒分割,比較直觀的做法是對每一幅偏光序列圖下的圖像進行分割,然后將多幅圖像的分割結果進行合并,得到最后的分割結果。但是通過實驗發現,該做法存在這樣的問題:由于巖石圖像本身的復雜性和多樣性,分割中存在許多誤分割,對多幅圖像的處理圖進行疊加處理,容易將多幅圖像的錯誤分割結果相疊加。因此本文未選擇上述方法,而采用先將序列圖像疊加到一起,再做分割處理的方法。
2.1 偏光序列圖像的疊加
不同的顆粒在正交偏光鏡下的明暗變化的趨勢不同,這種趨勢如果相同,則可以合理的認為是一個顆粒的概率較大[3],本文將偏光鏡下采集的不同序列圖像之間的變化差值累加后得到疊加圖像,如式(1)、式(2)所示:
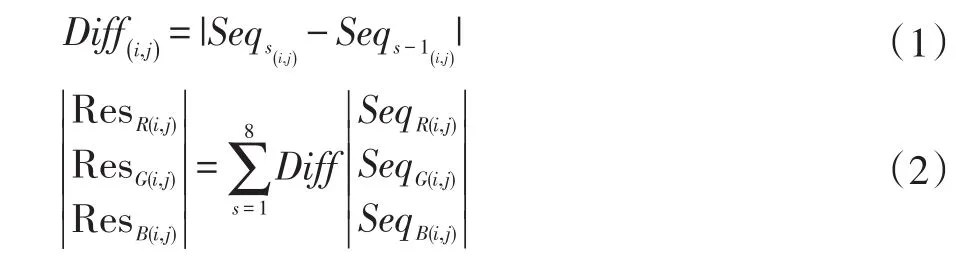
2.2 標記分水嶺分割
本文對疊加后的圖像采用標記分水嶺方法進行顆粒分割,分水嶺分割[7]是一類目前使用最為廣泛的顆粒形態學分割方法。其中H-minima[8]是一種常見的標記選擇方法,采用梯度圖像中的區域極小值作為種子點[9],實現目標分割。本文根據文獻[10]選取方向測度的極小點作為標記種子點,將每個像素點的鄰域擴充到7×7,有效抑制了因為噪聲或者顆粒形狀不規則等因素而產生的多個虛假種子點,在一定程度上解決了基于梯度標記分水嶺分割方法產生的嚴重過分割現象。
如圖3為采用分水嶺分割后用隨機顏色填充顆粒,并將背景色置為黑色后的圖,由此可以清晰看出,基本所有的顆粒都被提取出來。但在部分區域,如圖3中的標記區域,仍存在過分割的現象。

圖2 正交偏光下采集的序列圖像的疊加圖像

圖3 分水嶺分割后的圖像
3 過分割區域聚類
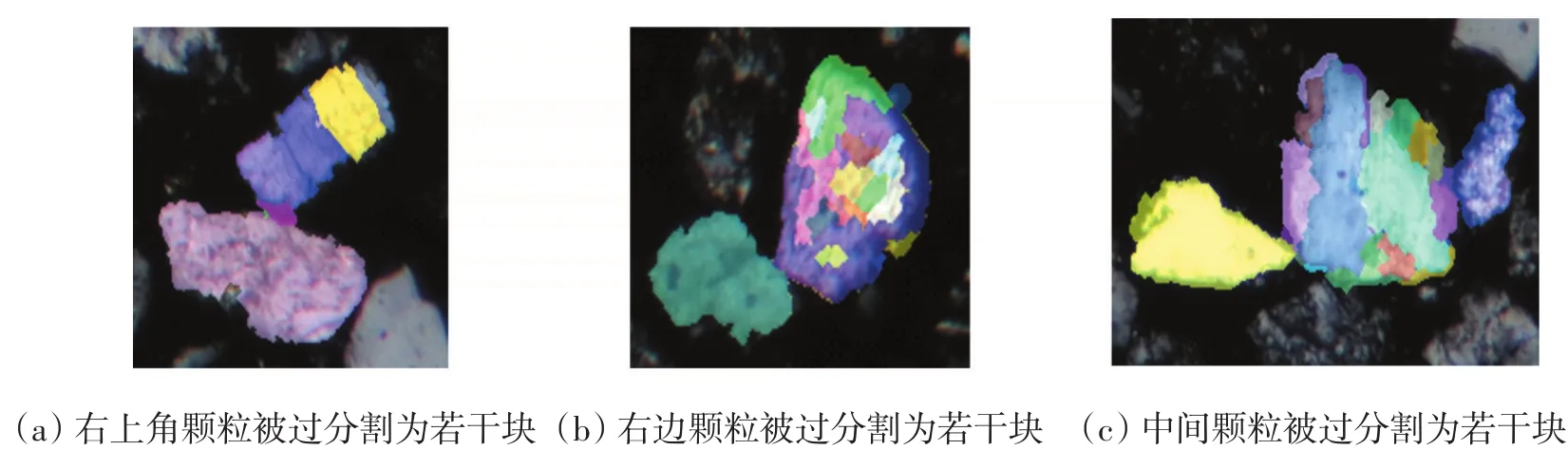
圖4 過分割的粘連區域
由圖3中標記可見,對于相毗鄰的顆粒,可能會出現將其中的顆粒過分割成為若干個小區域的現象。圖4是將這部分區域放大后以一定透明度附加到原本的顆粒上的圖像。如圖4(a)所示,由于右上角的顆粒被過分割,導致原本只有兩個顆粒的該區域被分割成多個區域。針對這種現象,本文首先對過分割的圖像區域進行角度,面積,位置特征提取,然后采用“自底向上”的AGNES層次聚類算法進行聚類,將該區域聚合為符合實際情況的分割效果。
3.1 圖像區域特征表示
以圖5中的兩個顆粒為例,標記上方顆粒為Grain-U,下方顆粒為Grain-D,其中Grain-U由于過分割導致被分成若干小的區域。
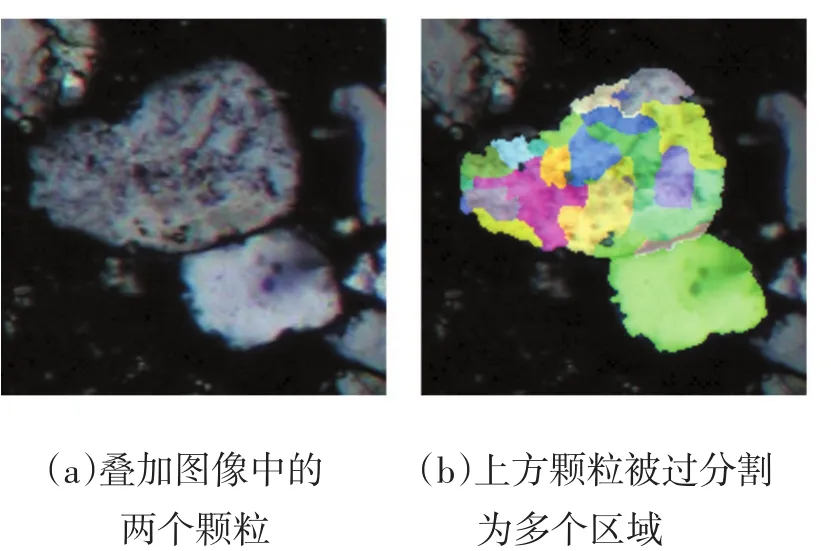
圖5 被過分割的兩個顆粒
本文從以下幾個方面來描述區域的特征:
(1)區域的角度特征
由于巖石顆粒正交偏光的周期消光性,正交偏光鏡下旋轉360°,顆粒會出現4次消光現象,每90°為一個周期[11]。如圖 6(a)(b)(c)(d):分別是在正交偏光0°,45°,60°,105°下的顆粒圖像,可見上下兩個顆粒在不同偏光角度下呈現出來的亮度是不一樣的,每個區域在一個周期內都存在亮度的最小值和最大值,且不同顆粒的亮度峰值所在角度不同。圖6(e)是Grian-U中的區域亮度變化折線圖,由于共同的消光性,雖然被過分割為多個不同的區域,但其亮度變化的趨勢一樣,均在75°達到峰值;而未被過分割的Grian-D顆粒在60°時亮度達到峰值。
因此可以用該峰值的角度來表征該區域的角度特征,如式(3)所示:

其中θLmax表示該區域亮度達到峰值時的角度,以π/2為底對數據進行標準化操作,θ'為標準化之后的角度值。
(2)區域的面積特征
由于分水嶺的過分割現象,部分顆粒被分割成了許多小的區域。而這些小的區域的面積相對于其毗鄰顆粒的面積較小,具有相似性,因此面積可以作為聚類的一個特征,如式(4)所示:

S'代表該區域的相對面積的大小,Ssum表示過分割區域的總面積,S為當前區域的面積。
(3)區域的位置特征
由圖5(b)可以看出,Grian-U過分割區域的重心坐標相對集中,而Grian-D的重心坐標距離其他區域的相對較遠。因此可以用區域的重心點坐標來表征該區域所在的位置,如式(5)所示:

(X',Y')代表當前區域重心坐標的相對位置。其中W、H分別表示圖像的寬和高,(X,Y)為當前區域的重心坐標。
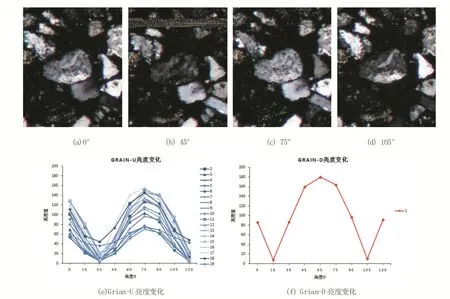
圖6 同一顆粒不同角度的明暗變化
根據公式(3)(4)(5)計算后的特征量值都被限定到[0,1]之間,從而組成一個四維的特征向量V={θ',S',X',Y'}.
3.2 過分割區域聚類
本文采用“自底向上”AGNES層次聚類算法,在不同層次對數據進行劃分,從而形成樹形的聚類結構[12]。先將過分割區域內所有的單個區域看成一個初始聚類簇,然后找出距離最近的兩個簇進行合并,該過程不斷重復,直至達到終止聚類個數。本文計算簇間距離使用average linkage距離,簇間距離等于兩組對象之間的平均距離。給定聚類簇Ci和Cj,其距離定義為:
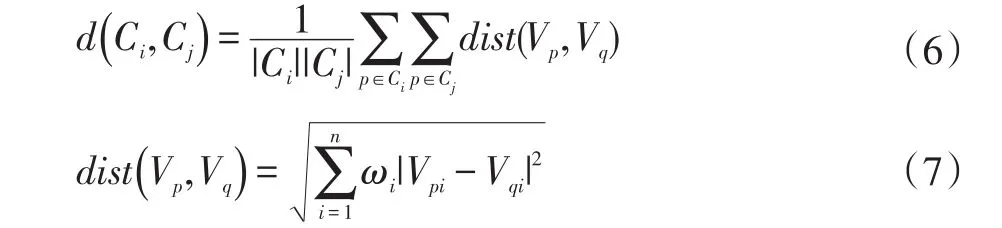
其中d(Ci,Cj)表示不同簇Ci和Cj之間的距離,dist(Vp,Vq)是兩個區域p和q之間的歐氏加權距離,Vpi表示這個區域在i分量的特征值,ωi表示在i分量的權值。經大量試驗,區域的角度特征和面積特征在聚類作用中比重較大,取亮度權重和面積權重ω1=ω2=5;坐標位置權重ω3=ω4=3。
為了得到符合實際的聚類個數,在使用層次聚類的過程中,每一次兩個相近簇合并后,需要對該次合并的有效性進行判斷,即衡量當前聚類的有效性。首先定義層次聚類中的成本函數為:

其中,k是簇的個數,x表示簇中的數據,Ti是第i個簇中元素的集合;Ci表示第i個簇的中心,m為當前簇中的元素個數。成本函數是各個簇畸變程度之和,若簇內部的成員彼此間越緊湊則畸變程度越小,反之,若簇內部的成員彼此間越分散則畸變程度越大。
根據文獻[13],可以通過肘部法則來估計聚類數量。肘部法會把不同k值的成本函數值反映在曲線上。隨著k值的增大,每個簇中包含的樣本數會減少,樣本離其中心會更近,因此平均畸變程度會減小。但是,隨著k值繼續增大,平均畸變程度的改善效果會不斷減低。當Jk減少緩慢時,就認為即使進一步增大聚類數,畸變程度的改善效果也并不能增強,則此時的這個“肘點”對應的k值就是最佳聚類數目,如圖7(a)。上述出現明顯“肘部”的情況比較常見,但是Jk值的變化也可能比較平緩沒有明顯的拐點,如圖7(b),這時可以認為該區域最終聚為一類。
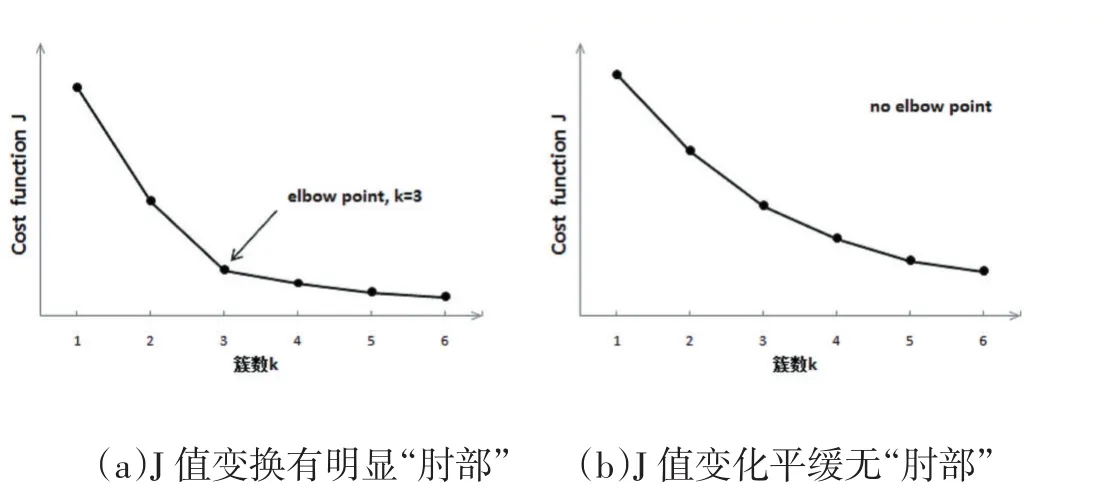
圖7 J隨k值的變化曲線
本文設定當聚類數小于設定數kmax時,即當k取k=1,2,…,kmax,計算其成本函數。根據計算的結果得到Jk值變化對應的k值,則此k值就為最終的聚類個數,如果隨著聚類數目的減小,Jk的變化幅度始終相當,變化曲線上沒有明顯的拐點,則把這個區域歸為一類。
聚類過程為:首先設定一個過分割區域內的所有區域各為一簇,根據公式(6)計算所有簇間距離,將距離最近的兩個簇合并,然后更新整個簇的個數;再計算新的簇之間的距離,根據距離最近原則再合并兩個簇,如此反復。當簇個數小于等于設定值kmax后,開始計算其成本函數 Jk,并保存每次更新的簇的結果,直到最終聚為一類。
每合并一簇后計算每次變化的幅度:

計算ηk的平均值kavg,比較每次聚類后當前幅度值與平均值的大小,若滿足ηk≥δ×kavg,則判斷其為“肘部”,對應的k值即為最佳聚類個數,k值對應的聚類結果即為最終結果。如果均不滿足,即不存在明顯“肘部”,此時k取1,聚為一類。經過試驗,當設定δ=2時,聚類結果較符合實際情況。
將同一類區域填充為同一種顏色,根據上述算法,圖5的最終聚類圖如圖8所示:
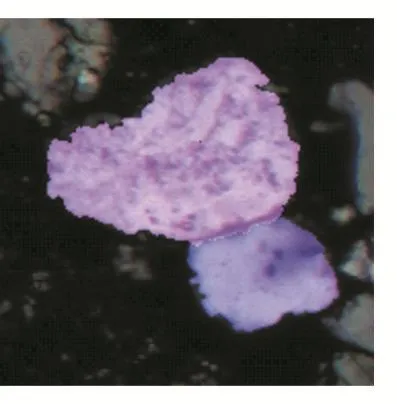
圖8 Grain-U和Grain-D最終聚類圖
再分別對圖4中的過分割區域進行聚類,結果如圖9所示,可以看出,本文算法成功將過分區域聚類為符合實際情況的結果。
4 實驗結果與分析
本文對二組實際拍攝的偏光序列圖進行顆粒分割,并與文獻[6]中的顆粒分割方法算法進行對比。
顆粒分割結果如圖10所示,其中:(a)(d)分別為兩組偏光序列圖進行差分疊加后的圖像;(b)(e)分別為通過文獻[6]中SRM算法分割后的效果圖;(c)(f)分別為本文方法對顆粒的分割效果圖。文獻[6]中先對每一張圖片進行分割后再合并,提取到的顆粒比較多,但是過分割現象嚴重。本文中先將序列圖合并后再進行分割,并且對過分割區域進行聚類合并,過分割現象得到很好的抑制,使得結果較于文獻[6]的方法更符合實際需求。
5 結語
本文討論了一種正交偏光圖像序列圖的顆粒分割算法,首先采集不同偏光角度下的序列圖,對序列圖進行疊加融合后再基于分水嶺算法分割將目標顆粒提取;然后對過分割區域提取角度、面積、位置等特征;最后通過AGNES聚類算法將過分割的顆粒聚類到一起,從而完成顆粒的分割提取。

圖9 過分區域聚類后效果圖

圖10 文獻[3]算法以及本文算法對比效果圖
實驗結果顯示,本文算法通過先分離后聚合的方式,成功將過分割的區域融合。但對于沒有在分水嶺階段中沒有提取到的顆粒,本文算法不能將其分割出來,可在這方面繼續加以研究。
[1]徐耀鑒.巖石學[M].北京:地質出版社,2007.
[2]Obara B.A New Algorithm Using Image Colour System Transformation for Rock Grain Segmentation[J].Mineralogy and Petrology,2007,91(3-4):271-285.
[3]Gorsevski P V,Onasch C M,Farver J R,et al.Detecting Grain Boundaries in Deformed Rocks Using a Cellular Automata Approach[J].Computers&Geosciences,2012,42(3):136-142.
[4]楊宗瑞.基于偏光序列圖像的巖石顆粒分割及礦物分[D].四川大學,2014
[5]Gorsevski P V,Onasch C M,Farver J R,et al.Detecting Grain Boundaries in Deformed Rocks Using a Cellular Automata Approach[J].Computers&Geosciences,2012,42(3):136-142.
[6]吳擁,蘇桂芬,滕奇志,等.巖石薄片正交偏光圖像的顆粒分割方法[J].科學技術與工程,2013,13(31):9201-9206.
[7]Beucher S,Meyer F.Segmentation:The Watershed Transformation.Mathematical Morphology in Image Processing[J].Optical Engineering,1993,34(5):433-481.
[8]Chanho J,Changick K.Segmenting Clustered Nuclei Using H-minima Transform-based Marker Extraction and Contour Parameterization[J].IEEE Transactions on Bio-medical Engineering,2010,57(10):2600-4.
[9]Li B,Pan M,Wu Z.An Improved Segmentation of High Spatial Resolution Remote Sensing Image Using Marker-based Watershed Algorithm[C].International Conference on Geoinformatics.IEEE,2012:1-5.
[10]楊海軍,梁德群,畢勝.基于圖象方向性信息測度的圖象象素分類[J].中國圖象圖形學報,2001,6(5):429-433.
[11]Fueten F,Goodchild J S.Quartz C-axes Orientation Determination Using The Rotating Polarizer Microscope[J].Journal of Structural Geology,2001,23(6-7):895-902.
[12]周志華.機器學習[M].清華大學出版社,2016.
[13]Bholowalia P,Kumar A.EBK-Means:A Clustering Technique based on Elbow Method and K-means in WSN[J].International Journal of Computer Applications,2014.

