基于雙eN方法的翼身組合體流動轉捩自動判斷

朱震，宋文萍，韓忠華

西北工業大學 航空學院 翼型葉柵空氣動力學國家級重點實驗室，西安 710072

出于環保性和經濟性的要求，通過減阻設計提升民機性能是設計師們長期追求的目標。美國國家航空航天局(NASA)的ERA(Environmentally Responsible Aviation)項目[1]和歐洲航空研究咨詢委員會(Advisory Council for Aeronautical Research in Europe，ACARE)發布的《歐洲航空2050展望》[2]均指出，進一步減少目前客機的阻力，減少二氧化碳排放和燃油的消耗是航空技術領域關注的熱點研究方向，對于提高新型客機性能具有重要的意義。目前，如果想要在減阻設計方面取得較大突破，自然層流機翼技術是一個值得期待的研究方向[3]。經過多年發展，抑制Tollmien-Schlichting(T-S)波不穩定擾動的自然層流翼型技術已經較為成熟，但民機廣泛采用的后掠機翼設計給實現大范圍自然層流減阻設計帶來了挑戰。民機一般采用大展弦比后掠機翼設計推遲激波產生，減小激波阻力，增大巡航速度以提高巡航效率因子。但后掠機翼的邊界層由于受到橫向壓力梯度的影響，速度型存在橫流(Cross-Flow，CF)分量，橫流速度型具有拐點，很容易出現橫流不穩定性(CFI)[4]導致的轉捩。而機身的三維位移效應會進一步增強機翼表面橫流流動，可能導致原本設計的具有較大范圍自然層流的后掠機翼因機身影響提前發生轉捩。因此面向翼身組合體外形，發展可靠實用的轉捩自動判斷方法，是當前發展自然層流減阻設計技術的急需；通過翼身組合體流動轉捩判斷研究，進一步分析機身對機翼轉捩的影響，對于自然層流后掠機翼的設計具有指導性意義。

目前國外研究機構已經圍繞翼型、機翼邊界層流動轉捩判斷開展了大量的研究工作[5-20]。而針對翼身組合體復雜三維外形，國外開展的邊界層轉捩判斷方法研究相對較少，且主要使用簡化的eN數據庫轉捩判斷方法。如法國宇航院(ONERA)在其雷諾平均Navier-Stokes(RANS)方程求解器elsA中加入了Arnal[9]和Casalis[12]等發展的eN數據庫方法，分別用來計算T-S波和CF波誘導的轉捩，并開展了帶增升裝置的翼身組合體外形的轉捩判斷研究[21]。德國宇航院(DLR)在其結構化網格RANS求解器FLOWer[17]和非結構/混合網格RANS求解器TAU[22]中加入了eN數據庫方法，開展了三維復雜外形的轉捩判斷研究。美國斯坦福大學的Lee和Jameson[23]開展了基于耦合eN數據庫方法的RANS求解器的層流機翼設計工作。eN數據庫方法是完全eN方法的近似和簡化。eN數據庫方法并不求解線性穩定性方程，而只是根據邊界層的形狀因子、速度型拐點信息等部分特征參數，在數據庫中查詢事先求解的平板邊界層不穩定擾動累積放大因子的包絡線。而完全eN方法則是通過求解線性穩定性方程，得到真實機翼邊界層的不同頻率或波數的不穩定擾動波的累積放大因子發展規律。最近，以γ-Reθ t轉捩模型為基礎發展橫流轉捩判斷方法的研究也逐漸開展起來。2016年，Grabe等[24]使用引入C1橫流判據和He橫流判據的γ-Reθ t轉捩模型開展了DLR-F4翼身組合體的機翼邊界層轉捩判斷研究。

目前，國內也鮮有使用完全eN方法對翼身組合體復雜三維外形開展轉捩判斷的研究工作，國內已開展的轉捩判斷研究工作主要針對翼型、機翼繞流進行。在使用穩定性理論和eN方法進行的后掠機翼邊界層穩定性及轉捩判斷研究方面，張坤和宋文萍[25]通過線性穩定性理論(Linear Stability Theory，LST)，左歲寒等[26]通過線性拋物化穩定性方程(Linear Parabolized Stability Equations，LPSE)開展了機翼邊界層轉捩判斷研究。孫朋朋[27]、靖振榮[28]和黃章峰[29]等通過LST開展了一系列的后掠機翼邊界層穩定性及轉捩研究，以及使用擴展的O-S方程(Extended Orr-Sommerfeld equation，EOS)和LPSE進行了機翼邊界層的橫流穩定性分析和轉捩判斷研究。韓忠華等[30]開展了基于線性穩定性理論的雙eN方法耦合RANS求解器進行自然層流后掠機翼優化設計的工作。同樣，國內近期也開展了以γ-Reθ t轉捩模型為基礎，發展橫流轉捩判斷方法的研究，如徐家寬[31-32]、史亞云[33]、戚瓊[34]、鞠勝軍[35]等使用添加了橫流判據的γ-Reθ t轉捩模型開展了三維流動中的橫流轉捩判斷研究。

本文使用多塊結構化網格和RANS求解器，耦合邊界層方程求解和基于線性穩定性理論的完全eN方法，發展了面向翼身組合體復雜三維外形流動的機翼轉捩自動判斷方法。采用雙eN方法，針對邊界層方程求解得到的邊界層速度型、溫度型等信息，通過求解線性穩定性方程，分別得到機翼邊界層T-S波和CF波的擾動累積放大因子曲線，通過閥值判斷轉捩位置。該方法不僅可以判斷轉捩位置，還可以得到轉捩誘發機制，能夠為自然層流設計提供指導。針對翼身組合體外形繞流，為了便于實現轉捩自動判斷，本文采用一種通用的結構化網格拓撲結構處理方法，對所有翼面類部件適用。使用上述方法，針對中短程民機，開展翼身組合體繞流轉捩判斷研究，并通過與單獨自然層流機翼的對比，進一步研究了機身對后掠機翼邊界層橫流速度型、橫流不穩定擾動放大率和轉捩位置的影響規律，可為考慮機身影響的自然層流后掠機翼減阻設計提供支持。

1 數值方法

1.1 完全雙eN轉捩判斷方法

對機翼邊界層的轉捩位置進行準確判斷是自然層流機翼減阻設計的關鍵技術之一。由層流到湍流的轉捩誘發機理復雜，影響因素眾多，轉捩判斷問題目前仍是流體力學中尚未完全解決的問題之一。基于線性穩定性理論的eN方法是目前在工程實踐中得到最廣泛認可的轉捩判斷方法[36]，因此本文基于線性穩定性分析的完全eN方法判斷轉捩。針對自然層流翼身組合體外形，采用空間放大理論分析小擾動，進行機翼邊界層轉捩自動判斷。eN方法由Smith[37]和Ingen[38]等首次提出，其思想是對邊界層流動中的小擾動進行線性穩定性分析，如果擾動逐漸衰減，則是穩定的，如果擾動被放大，則是不穩定的。對于不穩定的擾動，從其開始放大處起，沿下游方向計算其累積的線性放大倍數，當累積放大倍數到達擾動開始放大處振幅的eN倍時，認為轉捩發生。基于平行流假設的三維小擾動形式為

(1)

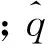
(2)

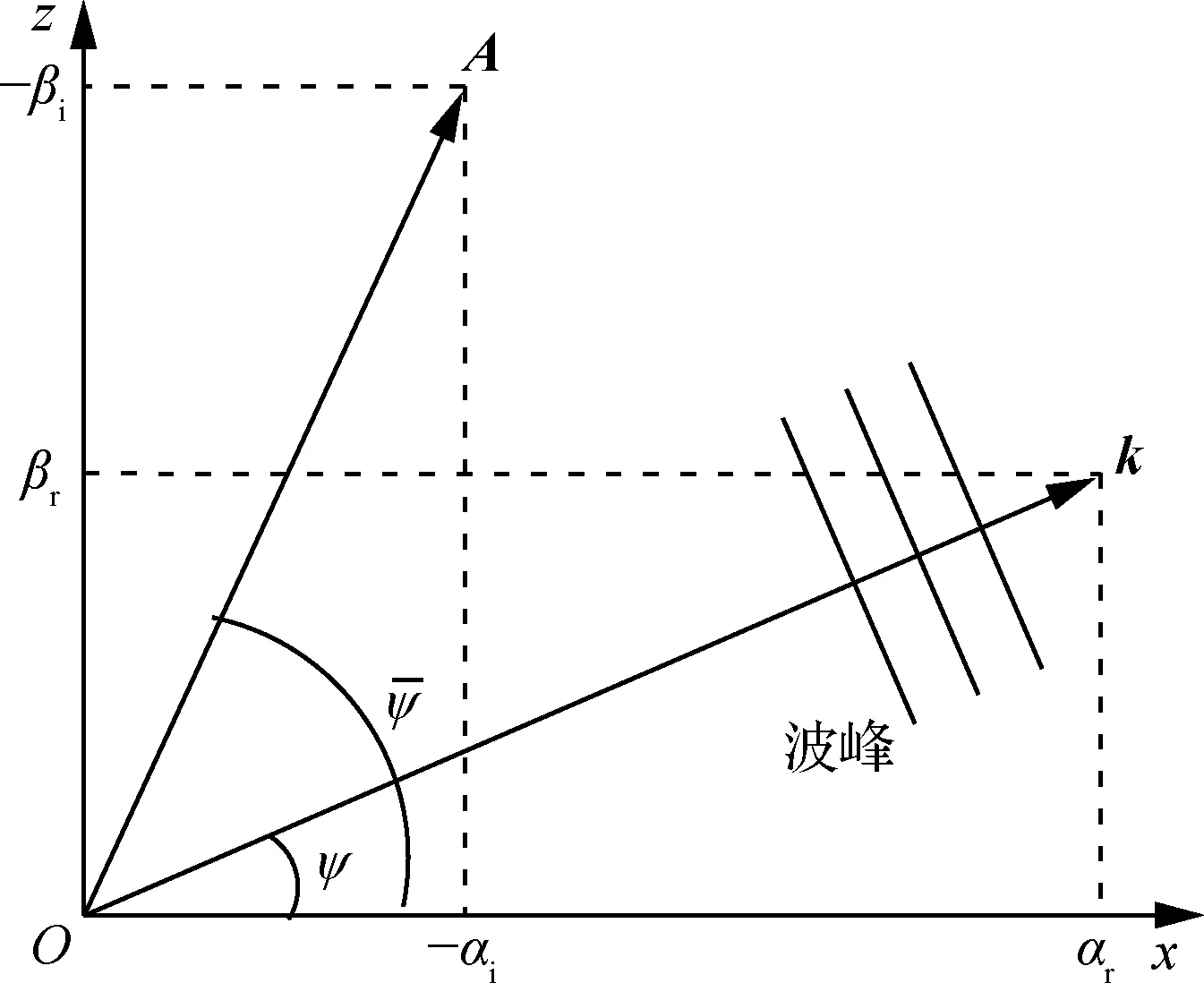
圖1 空間放大理論中擾動波數矢量與擾動增長矢量 Fig.1 Disturbance wave number vector and disturbance amplification vector in spatial amplification theory

基于線性穩定性理論的完全eN方法，對機翼邊界層信息求解線性穩定性方程，進行擾動累積放大因子的計算，而不對數據庫進行查詢，因此不存在近似和簡化。完全eN方法進行邊界層轉捩位置的判斷分兩步進行：① 計算中性曲線，即擾動的穩定區域和不穩定區域的分界線。通過中性曲線就可以確定不穩定擾動的頻率范圍、波數范圍和不同擾動各自開始被放大的位置；② 按照適當的積分策略，對這些頻率的擾動放大率從中性曲線下半支出發，沿著擾動傳播路徑進行積分，得到擾動累積放大因子N。這兩步都需要求解三維可壓縮線性穩定性方程，其數值求解方法為：① 采用連續法獲得具有較高精確度的特征變量初值；② 將高階的線性穩定性控制方程組轉化為一階的控制方程組；③ 采用中心差分方法離散控制方程組；④ 采用牛頓法線化離散后的控制方程組；⑤ 采用塊矩陣消去法求解方程組。

1.1.1 固定波角的方法

對于T-S波不穩定(TSI)擾動，原有的包絡線方法[39]始終尋找擾動放大率最大的波角方向進行積分，如果存在較強的CF波，可能會錯誤地把CF波擾動積分到T-S波擾動累積放大因子NTS中。本文對包絡線方法進行了改進，采用固定波角的方法計算T-S波擾動累積放大因子，即

(3)

式中：f為頻率；x0為中性曲線計算出的小擾動開始放大的x位置。本文采用固定波角方法，選擇擾動波波角(波數矢量與x軸的夾角)ψ= 0° 方向，即邊界層外邊界速度方向，計算不同頻率f擾動的放大率并進行積分，因此能夠保證始終對T-S波擾動進行積分，不會混入CF波擾動。

1.1.2 同時固定βr和f的方法

對于CF波不穩定(CFI)擾動誘導的轉捩，本文采用同時固定βr和f的方法計算CF波擾動累積放大因子，即

(4)

式中：NCF為CF波擾動累積放大因子；βr為橫流展向波數；f=0 Hz時為橫流駐波。針對本文中短程民機巡航狀態，選擇對不同展向波數βr的橫流駐波進行擾動放大率的積分，計算橫流擾動累積放大因子NCF。對于CF波不穩定擾動，基于平行流假設的線性穩定性理論沒有考慮擾動幅值本身的變化存在一定偏差。根據黃章峰等[30]的研究，線性穩定性方程計算得到的擾動放大增長因子與考慮擾動幅值本身變化的拋物化穩定性方程相比，形態趨勢一致但相對偏小。因此本文采用線性穩定性方程仍可較為有效地預測CF波不穩定誘導的轉捩，但其對應的轉捩閥值相對較小。

1.1.3 雙eN轉捩判斷方法

雙eN方法是一種轉捩判斷方法的構架，可以針對T-S波和CF波選擇不同的擾動放大率積分策略構建不同的轉捩判斷方法。對于T-S波的擾動放大增長因子NTS，采用1.1.1節描述的固定波角的方法計算；對于CF波的擾動放大增長因子NCF，采用1.1.2節描述的同時固定βr和f的方法計算。根據事先給定的轉捩閥值[(NTS)tr,(NCF)tr]，確定機翼邊界層的轉捩位置。如果NTS先到達其對應的閥值(NTS)tr，就認為T-S波誘導轉捩發生。如果NCF先到達其對應的閥值(NCF)tr，則認為邊界層流動轉捩由CF波不穩定性觸發。

1.2 RANS求解器與轉捩判斷方法耦合流程

采用耦合完全雙eN方法的三維RANS求解器PMNS3D[39]開展面向翼身組合體外形的機翼邊界層轉捩自動判斷方法研究。求解器主要由3個模塊構成：① 三維RANS求解器模塊。本模塊采用多塊結構化網格、有限體積法、LU-SGS(Lower-Upper Symmetric Gauss-Seidel)時間推進、多重網格加速收斂技術。湍流流動模擬采用Spalart-Allmaras(S-A)湍流模型。此模塊對翼身組合體黏性繞流進行數值模擬，并從計算結果中提取機翼邊界層外邊界流向速度ue、展向速度we、溫度Te等流動參數，作為三維層流邊界層方程求解的邊界條件。② 三維層流邊界層方程求解模塊。因直接從RANS方程解提取的層流邊界層信息難以滿足線性穩定性分析的精度要求，此模塊通過非正交貼體坐標系對機翼邊界層方程進行求解，可在對網格量沒有過高要求的條件下，得到滿足三維邊界層穩定性分析所需的高精度速度型u、溫度型T以及它們在物面法向的一階導數u′、T′和二階導數u″、T″。③ 基于線性穩定性理論的雙eN轉捩判斷模塊。通過對邊界層內部的速度型、溫度型進行線性穩定性分析，使用完全雙eN方法得到邊界層轉捩的位置xtr，并反饋給三維RANS求解模塊。重復迭代至轉捩位置收斂，依據收斂的轉捩信息繼續RANS方程的迭代求解，直至最終達到流場收斂標準。求解器中不同模塊耦合流程如圖2所示。

1.3 翼身組合體結構化網格拓撲

本文使用多塊結構化網格，開展面向翼身組合體的雙eN轉捩自動判斷方法研究。對于三維復雜外形，如果使用非結構網格，雖沒有嚴格的網格拓撲結構要求，但在計算擾動累積放大因子時，因其相鄰網格單元的無序性，需要采取專門的積分路徑確定方法[36]。本文針對復雜外形流動，建立了一種便于實現轉捩自動判斷的，且通用的翼身組合體結構化網格拓撲結構處理方法，對所有翼面類部件均適用，在計算擾動累積放大因子時，積分路徑可以直接使用機翼表面網格線，相對非結構網格較為簡單便利。

具體方法如下：包裹整個機翼(不包含翼梢端面和機翼后緣厚度端面)邊界層生成一塊完整的C型單塊網格，網格塊示意圖如圖3中線框所示。

對于這塊網格，執行圖2中右側虛線框內的轉捩自動判斷流程。因為機翼表面流向網格線完整連續，這樣在計算擾動累積放大因子時，積分路徑可以直接使用機翼表面網格線。如果需要對平尾、垂尾等翼面的邊界層進行轉捩自動判斷，上述方法同樣適用。而機身部分則不存在網格拓撲結構的特殊要求，可按照常規方法自由生成網格。

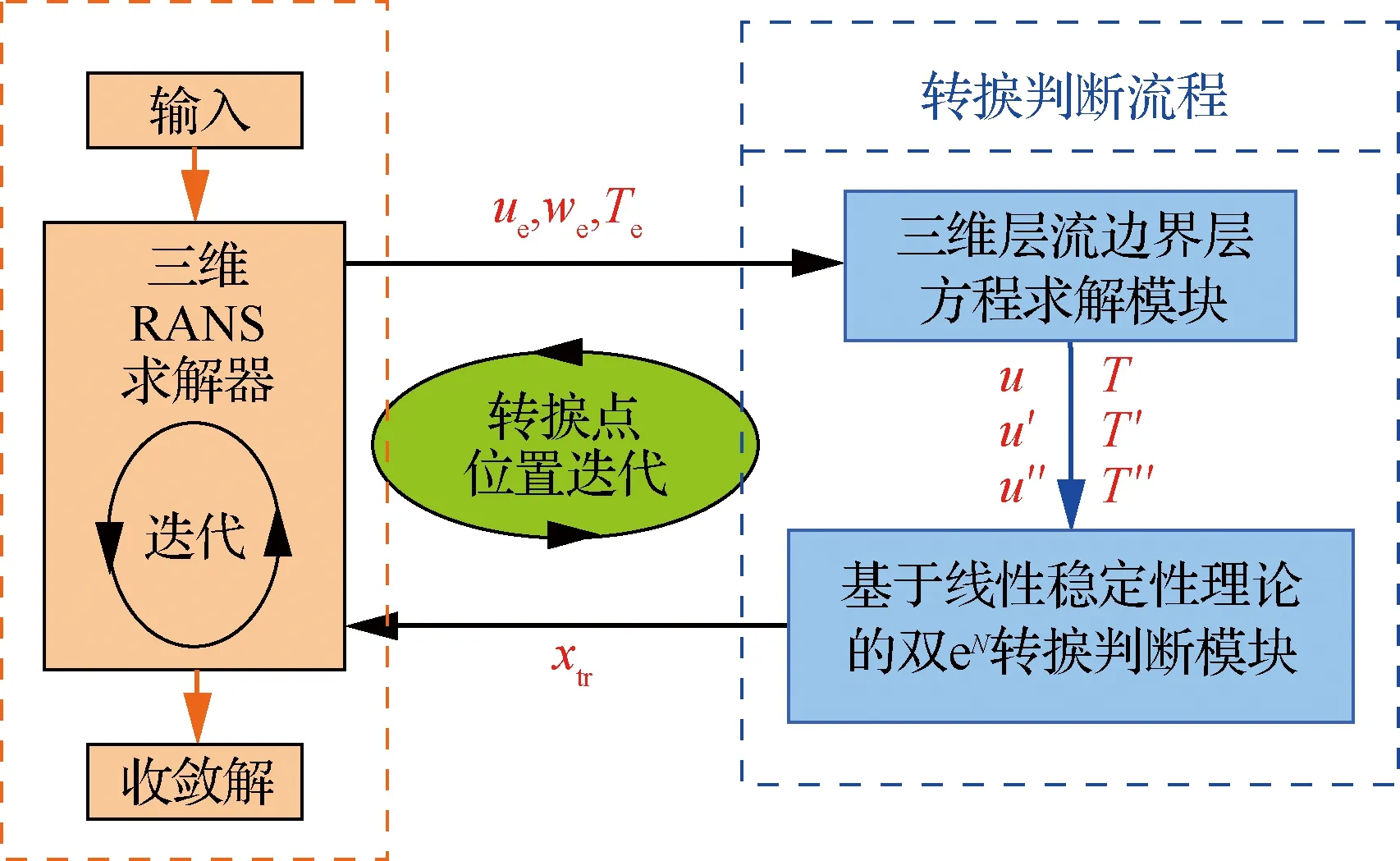
圖2 RANS求解器耦合轉捩判斷模型的流程Fig.2 Coupling structure of RANS solver and transition prediction model

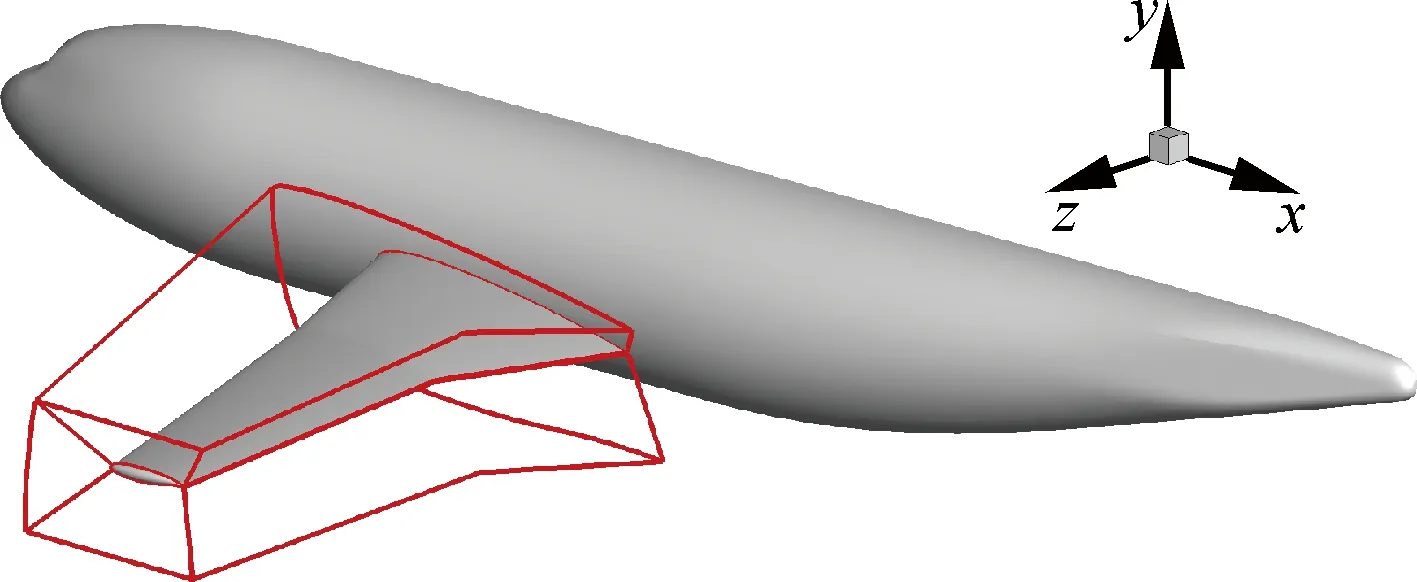
圖3 DLR-F4翼身組合體外形機翼邊界層轉捩 判斷結構網格拓撲Fig.3 Topology of structured grid for boundary layer transition prediction of wing of DLR-F4 wing-body configuration

2 方法驗證

采用本文方法，對DLR-F4翼身組合體外形機翼邊界層進行自由轉捩數值模擬，以驗證本文方法的正確性。計算狀態參考DLR在歐洲跨聲速風洞(European Transonic Wind tunnel，ETW)使用溫敏漆(Temperature Sensitive Paint，TSP)技術進行的翼身組合體機翼邊界層轉捩測量試驗[40]：馬赫數Ma= 0.785，雷諾數Re= 6.0×106，迎角α=-0.87°。計算網格為多塊結構化網格，y+約為0.8，整個翼身組合體網格量為420萬，其中包裹機翼的網格塊機翼流向分布185個網格點，展向分布49個網格點，法向分布105個網格點。采用S-A湍流模型模擬湍流流動。因風洞試驗湍流度高于真實飛行時高空安靜大氣湍流度，放大因子轉捩閥值[(NTS)tr, (NCF)tr]根據經驗取[10.5, 7.5]。

使用本文方法預測的機翼邊界層轉捩位置與試驗對比，如圖4所示，其中云圖為TSP試驗結果[40]，淺色部分為層流區域，深色部分為湍流區域；黑色實線為本文方法計算得到的機翼上表面轉捩線，和試驗轉捩位置基本一致。試驗結果TSP照片顯示機翼中外段轉捩線較為光滑，而機翼內段的轉捩線呈鋸齒狀。Fey等[40]分析認為這可能是因為機翼內段為橫流駐波不穩定性誘發的轉捩。此外，Grabe等[24]使用引入C1橫流判據和He橫流判據的γ-Reθ t轉捩模型對此狀態的機翼邊界層轉捩判斷研究也表明，機翼內段為橫流不穩定性主導的轉捩。而本文計算結果同樣表明，翼根區域為橫流駐波不穩定性擾動所導致的轉捩：圖 5為展向25%處站位A和47%處站位B的機翼上表面T-S波(虛線)和CF波(實線)不穩定性擾動放大積分因子N發展規律。由圖 5(a)可見，展向站位A轉捩位置(x/c)tr在流向x/c=0.34位置處，c為弦長，CF波擾動累積放大因子先于T-S波達到其對應閥值，即CF波不穩定性在此站位誘發轉捩。而圖 5(b)的展向站位B處為T-S波不穩定性誘發轉捩，轉捩位置(x/c)tr在流向x/c=0.45位置處。

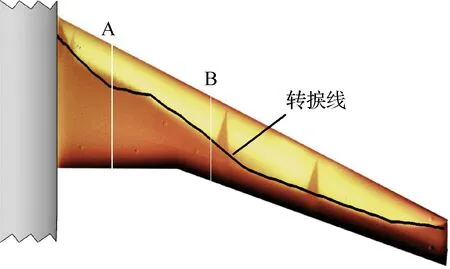
圖4 本文方法對DLR-F4機翼邊界層轉捩判斷結果 與TSP試驗照片[40]對比 Fig.4 Comparison of transition prediction result of DLR-F4 wing boundary layer by proposed method and TSP test image[40]

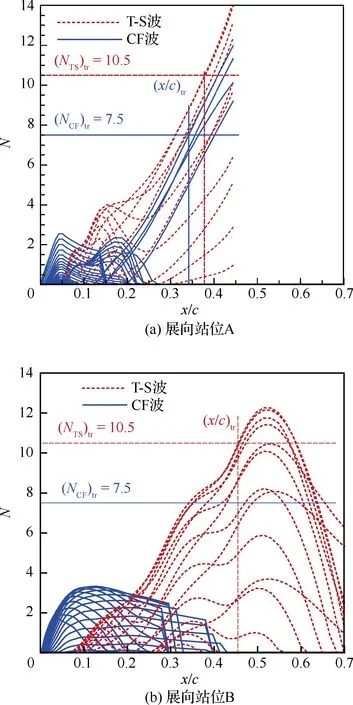
圖5 機翼上表面T-S波和CF波不穩定性擾動 放大積分因子Fig.5 Disturbance amplification integral factors of TSI and CFI on upper surface of wing

此算例表明，本文發展的完全雙eN方法不僅能夠對機翼邊界層轉捩位置進行較為準確的預測，同時能夠判斷出機翼內段轉捩是由橫流不穩定性主導的機理，與TSP試驗結果分析[40]和使用引入橫流判據的γ-Reθ t轉捩模型[24]的研究結論一致。驗證了本文方法的正確性，說明本文發展的方法能夠考慮機身的影響，實現對機翼邊界層的轉捩自動判斷，能夠支持下文開展的中短程民機翼身組合體流動轉捩判斷研究。

3 中短程民機翼身組合體流動轉捩判斷

3.1 翼身組合體的幾何外形

采用本文發展的基于雙eN的翼身組合體流動轉捩自動判斷方法，進行中短程民機翼身組合體流動轉捩自動判斷研究，并與單獨自然層流(NLF)機翼對比，進一步研究了機身對機翼邊界層轉捩的影響規律，可為中短程民機自然層流后掠機翼設計提供指導。本文研究的翼身組合體由自然層流后掠機翼和典型民機機身外形組成，翼身組合體外形見圖6。自然層流后掠機翼展弦比為10.5，梢根比為0.3，前緣掠角為19°。在機翼翼根翼梢均配置自然層流超臨界翼型NPU-LSC-72613[41]，翼梢無扭轉。機翼上反角為0°，安裝角為2°。

圖6 自然層流翼身組合體幾何外形Fig.6 Geometry shape of NLF wing-body configuration

自然層流超臨界翼型NPU-LSC-72613的設計思想[42]是在超臨界條件下通過弱激波抬高翼型后部的負壓，使得前緣到激波位置維持順壓梯度，抑制T-S波不穩定性，以保證在設計條件下獲得較大范圍的層流。圖7為NPU-LSC-72613翼型在Ma=0.72、Re=2.0×107、升力系數CL=0.6狀態下的表面壓力系數Cp分布及上下表面轉捩位置，從圖中可以看到翼型上下表面都存在有約50%～60%范圍的層流區域。

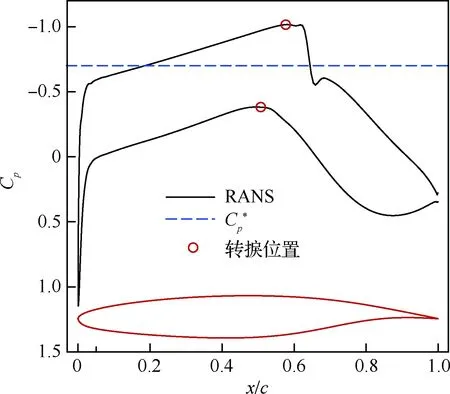
圖7 NPU-LSC-72613自由轉捩壓力系數分布(上表面轉捩位置(x/c)tr=0.577, 下表面轉捩位置(x/c)tr=0.507)Fig.7 Pressure coefficient distribution of NPU-LSC-72613 with free transition (transition location on upper surface: (x/c)tr=0.577; transition location on lower surface: (x/c)tr=0.507)

3.2 計算結果與分析

對翼身組合體繞流進行了轉捩自動判斷研究，并通過與單獨機翼進行對比，研究分析機身的存在對機翼邊界層橫流強度、CF波擾動累積放大因子和轉捩位置的影響規律。計算狀態為：Ma=0.78、Re=2.5×107，迎角為0°。計算網格為多塊結構化網格，y+約為0.8，整個翼身組合體網格量為420萬，在包裹機翼的單塊網格上，機翼流向分布185個網格點，展向分布49個網格點，法向分布105個網格點。單獨機翼網格采取和翼身組合體網格中的機翼表面完全相同的網格分布。采用S-A湍流模型模擬湍流流動。放大因子轉捩閥值[(NTS)tr, (NCF)tr]取為[10.5, 7.5]。

圖8為有/無機身時，機翼上下表面壓力分布云圖和轉捩線。可見，單獨機翼采取自然層流翼型有效抑制T-S波，較小的前緣后掠角抑制CF波，上表面維持了較大范圍(60%)的層流，下表面維持了一定范圍(30%)的層流。而對于翼身組合體外形，由于機身的存在，機翼翼根下表面轉捩位置大幅提前，雙eN方法結果表明此處為CF波不穩定誘導轉捩。

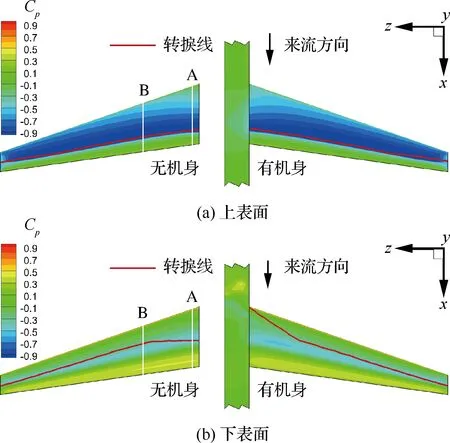
圖8 有/無機身時機翼表面壓力分布及轉捩線Fig.8 Pressure coefficient contours and transition lines of wing surface with/without fuselage

為了詳細分析機身對機翼邊界層轉捩和CF波不穩定性擾動的影響，圖9對翼身組合體和單獨機翼展向14%處站位A和36%處站位B的CF波擾動累積放大因子進行對比。從圖中可看出，由于機身的存在，翼身組合體相對于單獨機翼，橫流不穩定性有所增強。對比圖9(a)和圖9(b)可以看出上表面兩個站位處CF波擾動累積放大因子增強的幅度沿展向減小。對比圖9(c)和圖9(d)可見下表面規律同樣如此。

值得注意的是，圖9(c)中展向站位A下表面，因有機身導致CF波擾動累積放大因子曲線在前緣處快速增長，包絡線形成的峰值從6增長到8.4，超過閥值(NCF)tr=7.5誘發轉捩， 轉捩位置從(x/c)tr=0.55大幅提前到(x/c)tr=0.03的前緣處。而隨著與機身距離的增大，圖9(d)中展向站位36%處CF波不穩定擾動放大率的增強幅度變小，CF波擾動累積放大因子曲線未在前緣處到達閥值，轉捩位置僅從(x/c)tr=0.34提前到(x/c)tr=0.31。

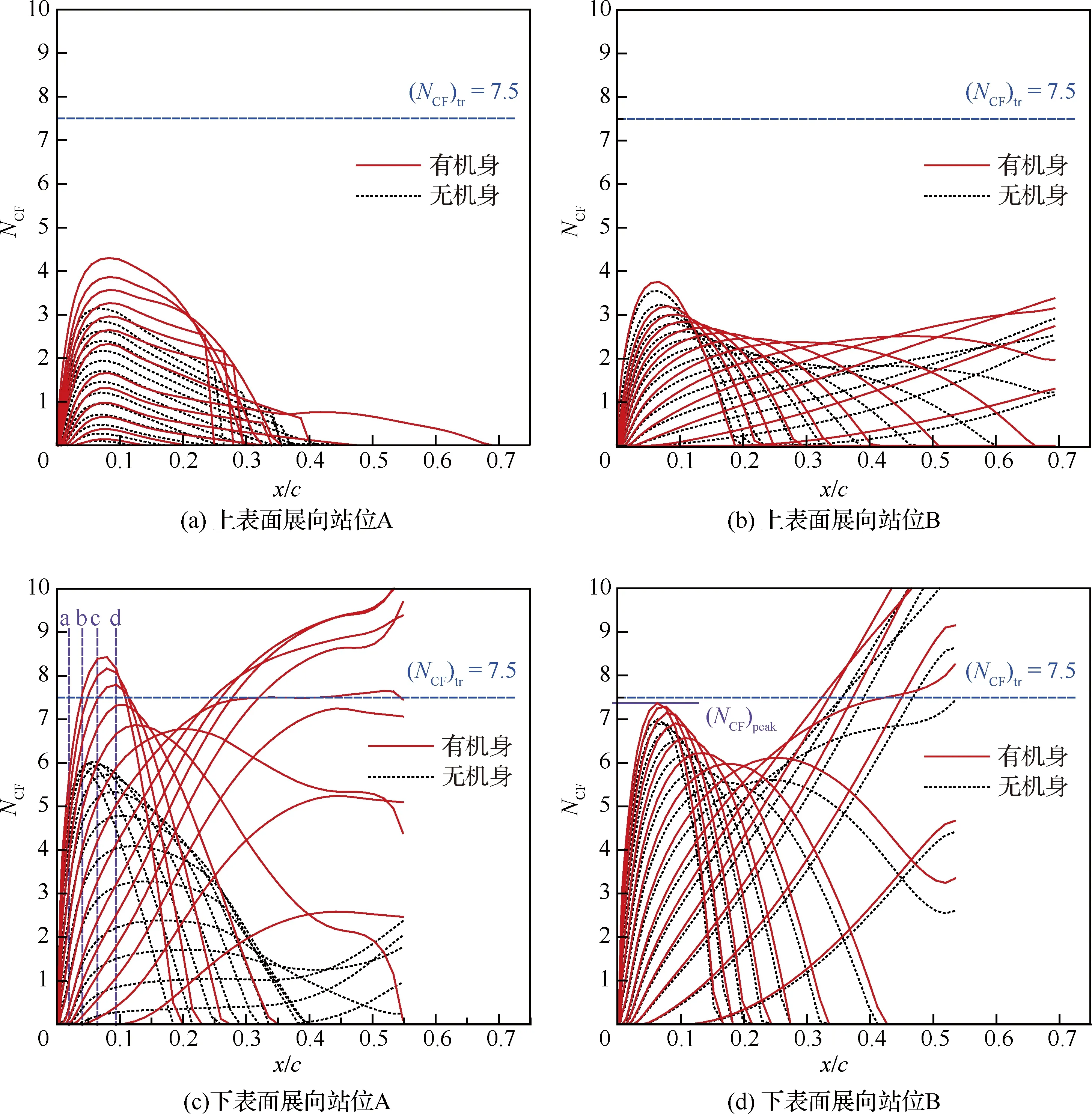
圖9 有/無機身時機翼上表面和下表面CF波擾動累積放大因子及(NCF)peak定義Fig.9 N factors of CFI on upper surface and lower surface of wing with/without fuselage and definition of (NCF)peak

通過對各站位尤其是靠近翼根的展向站位A處下表面的對比可以看出，對于自然層流后掠機翼的設計，CF波擾動累積放大因子曲線在前緣處的峰值尤為關鍵，因為此值一旦超過(NCF)tr，橫流不穩定性誘發的轉捩就會在前緣區域發生，必然無法實現較大的層流范圍。為了達到自然層流減阻的目的，這種情況應當盡量避免。

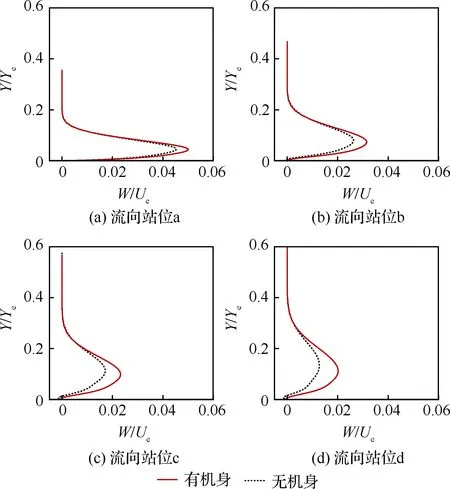
圖10 有/無機身時機翼下表面展向站位14%處 邊界層內橫流速度型Fig.10 CF velocity profiles inside boundary layers at spanwise 14% station on lower surface of wing with/without fuselage

為了更好地理解機身對機翼橫流不穩定擾動的影響，針對機身影響較大的展向站位14%，對其橫流擾動快速增長的前緣區域，即圖9(c)中a、b、c、d (x/c=0.019 0, 0.048 0, 0.064 4, 0.093 7) 這4個流向站位，進行了有/無機身時的機翼下表面邊界層內橫流速度型對比，見圖10，橫坐標W/Ue為無量綱展向速度，縱坐標Y/Ye為無量綱法向位置。橫流速度型拐點速度越大，拐點與物面距離越小，則橫流強度越大，對應的CF波不穩定擾動放大率越大。從圖中可見，在前緣加速區，隨流向速度的增大，4個流向站位處的橫流強度沿流向遞減。同時，每個流向站位處的橫流強度都因為機身三維位移效應，相對單獨機翼增強。這就是導致圖9(c)中展向站位14%處CF波擾動累積放大因子在前緣區域快速增長，且因有機身進一步增大的原因。

為了進一步研究機身對機翼的橫流不穩定擾動的影響沿著機翼展向的變化規律，對有/無機身時機翼下表面CF波擾動累積放大因子的包絡線進行對比，如圖11所示，其中黑色曲線為單獨機翼，紅色曲線為翼身組合體。從圖中可以看出，展向所有CF波擾動累積放大因子的包絡線形成的包絡面，因機身三維位移效應對機翼的影響整個鼓起，在機翼前緣區域形成一道沿機翼展向走向的山峰狀包絡面，距機身越近，其峰值越高，在翼根區域超過(NCF)tr，導致了翼根前緣區域CF波不穩定誘導轉捩的發生。

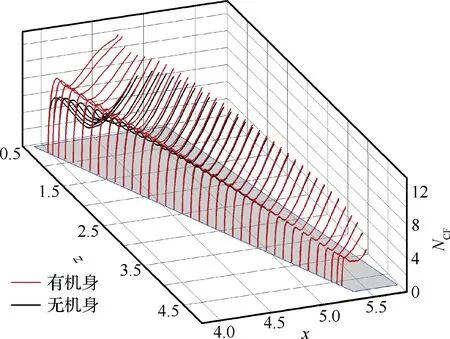
圖11 有/無機身時機翼下表面橫流擾動累積 放大因子包絡線Fig.11 NCF envelope curves on lower surface of wing with/without fuselage

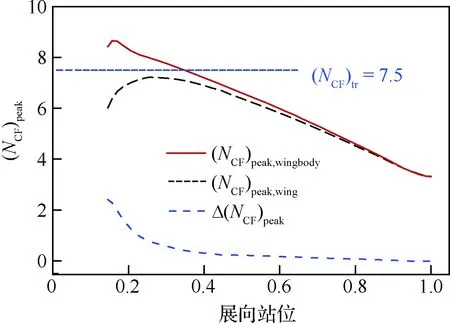
圖12 有/無機身時機翼下表面(NCF)peak沿展向 變化曲線及差值Fig.12 (NCF)peak on lower surface of wing with/without fuselage and delta value at spanwise station location

為更清晰觀察機身對機翼橫流轉捩位置的影響，圖12給出了NCF前緣區域峰值(NCF)peak(如圖9(d)中所示)沿展向的變化，同時給出了翼身組合體與單獨機翼的(NCF)peak的差值Δ(NCF)peak沿展向的變化。圖12中(NCF)peak,wing為單獨機翼下表面CF波擾動累積放大因子峰值沿展向變化曲線，因為單獨機翼翼根連接對稱面邊界條件，所以沿展向的橫向流動有一個發展過程：起初會呈現增強趨勢，很快達到最大值，然后隨著和對稱面的距離增大，機翼自身三維位移效應減弱，橫流不穩定擾動強度減小，(NCF)peak逐漸減小。(NCF)peak,wingbody為翼身組合體的機翼下表面CF波擾動累積放大因子峰值沿展向變化曲線，它處處高于(NCF)peak,wing曲線，即機身的三維位移效應增強了整個機翼的橫流強度，翼根處橫流不穩定擾動最強，隨著與機身距離的增大，強度沿展向逐漸減弱。Δ(NCF)peak為前兩者的差值，代表機身三維位移效應對機翼的干擾導致的(NCF)peak的增長量，因此沿展向單調遞減，此遞減趨勢呈現出兩個階段：機身影響在翼根區域較為明顯，展向站位14%的翼根處(NCF)peak相對單獨機翼增強40%，在展向站位30%處迅速減小到8%；機身影響在機翼中外段相對小很多，呈現出基本不變的趨勢。

圖12數據表明，單獨機翼展向所有(NCF)peak都未超過(NCF)tr，即7.5，故不會發生橫流不穩定性誘導的前緣轉捩，但由于機身三維位移效應的干擾，導致機翼下表面在展向站位35%內超過7.5，導致原本設計的自然層流后掠機翼，其內段部分轉捩位置提前到前緣區域，如展向站位14%處轉捩位置從(x/c)tr=0.55大幅提前到(x/c)tr=0.03的前緣處。

4 結 論

本文將求解線性穩定性方程的完全雙eN轉捩自動判斷方法推廣到了三維復雜外形。將針對實際應用設計的自然層流機翼配置到典型民機機身上，對此翼身組合體流動轉捩特征進行了研究，分析了機身的存在對機翼的影響。

1) 利用DLR-F4翼身組合體模型對所發展的方法進行了檢驗。結果表明該方法判斷出的轉捩位置與試驗結果吻合較好，驗證了方法的正確性。

2) 本文方法捕捉到了DLR-F4翼根處由橫流駐波導致的轉捩現象。表明本文發展的針對三維復雜外形的轉捩自動判斷方法不僅能夠較為準確地判斷轉捩位置，還能夠正確判斷轉捩誘發機制。

3) 對自然層流中短程民機外形的轉捩特征與橫流不穩定性的定量分析表明，機身的三維位移效應對流動產生了橫向的排擠，這增強了機翼邊界層的橫流強度，使得前緣區域的橫流不穩定性變強，導致翼根提前發生轉捩。

[1] COLLIER F, THOMAS R, BURLEY C, et al. Environmentally responsible aviation—Real solutions for environmental challenges facing aviation[C]∥27th Congress of the International Council of the Aeronautical Sciences 2010. Stockholm: ICAS Secretariat, 2010: 300-315.

[2] DARECK M, EDELSTENN C, ENDER T, et al. Flightpath 2050 Europe’s vision for aviation[R]. Belgium: Advisory Council for Aeronautics Research in Europe, 2011.

[3] HEPPERLE M. MDO of forward swept wings[C]∥KATnet II Multi-Disciplinary Design and Configuration Optimization Workshop, 2008: 28-30.

[4] ARNAL D, COUSTOLS E, JUILLEN J C. Experimental and theoretical study of transition phenomena on an infinite swept wing[J]. La Recherche Aerospatiale (English Edition), 1984, 1984(4): 39-54.

[5] DRELA M. Newton solution of coupled viscous/inviscid multielement airfoil flows[C]∥21st Fluid Dynamics, Plasma Dynamics and Lasers Conference, 1990: 1470.

[6] CEBECI T, STEWARTSON K. On stability and transition in three-dimensional flows[J]. AIAA Journal, 1980, 18(4): 398-405.

[7] MALIK M R. COSAL: A black-box compressible stability analysis code for transition prediction in three-dimensional boundary layers: NASA-CR-165925[R]. Washington，D.C.: NASA, 1982.

[8] MACK L M. Stability of three-dimensional boundary layers on swept wings at transonic speeds[C]∥IUTAM. Symposium Transsonicum III. Berlin Heidelberg: Springer, 1989: 209-223.

[9] ARNAL D. Transition prediction in transonic flow[C]∥IUTAM. Symposium Transsonicum III. Berlin Heidelberg: Springer, 1989: 253-262.

[10] ARNAL D, CASALIS G, JUILLEN J C. Experimental and theoretical analysis of natural transition on “infinite” swept wing[C]∥IUTAM. Laminar-Turbulent Transition. Berlin Heidelberg: Springer, 1990: 311-325.

[11] RADESPIEL R, GRAAGE K, BRODERSEN O. Transition predictions using Reynolds-averaged Navier-Stokes and linear stability analysis methods: AIAA-1991-1641[R]. Reston, VA: AIAA, 1991.

[12] CASALIS G, ARNAL D. ELFIN II subtask 2.3: Database method—Development and validation of the simplified method for pure cross-flow instability at low speed: ELFIN II-145[R]. Toulouse: ONERA-CERT, 1996.

[13] STOCK H W, HAASE W. Feasibility study of eNtransition prediction in Navier-Stokes methods for airfoils[J]. AIAA Journal, 1999, 37(10): 1187-1196.

[14] NEBEL C, RADESPIEL R, WOLF T. Transition prediction for 3D flows using a Reynolds-averaged Navier-Stokes code andN-factor methods: AIAA-2003-3593[R]. Reston, VA: AIAA, 2003.

[15] KRUMBEIN A. Automatic transition prediction and application to high-lift multi-element configurations: AIAA-2004-2543[R]. Reston, VA: AIAA, 2004.

[16] STOCK H W. Infinite swept wing Navier-Stokes computations with eNtransition prediction[J]. AIAA Journal, 2005, 43(6): 1221-1229.

[17] KRUMBEIN A. Automatic transition prediction and application to 3D wing configurations: AIAA-2006-0914[R]. Reston, VA: AIAA, 2006.

[18] CLIQUET J, HOUDEVILLE R, ARNAL D. Application of laminar-turbulent transition criteria in Navier-Stokes computations: AIAA-2007-0515[R]. Reston, VA: AIAA, 2007.

[19] KRUMBEIN A. eNtransition prediction for 3D wing configurations using database methods and a local, linear stability code[J]. Aerospace Science and Technology, 2008, 12(8): 592-598.

[20] PERRAUD J, ARNAL D, CASALIS G, et al. Automatic transition predictions using simplified methods[J]. AIAA Journal, 2009, 47(11): 2676-2684.

[21] PERRAUD J, CLIQUET J, HOUDEVILLE R, et al. Transport aircraft three-dimensional high-lift wing numerical transition prediction[J]. Journal of Aircraft, 2008, 45(5): 1554-1563.

[22] KRIMMELBEIN N, RADESPIEL R, NEBEL C. Numerical aspects of transition prediction for three-dimensional configurations: AIAA-2005-4764[R]. Reston, VA: AIAA, 2005.

[23] LEE J D, JAMESON A. Natural-laminar-flow airfoil and wing design by adjoint method and automatic transition prediction: AIAA-2009-0897[R]. Reston, VA: AIAA, 2009.

[24] GRABE C, SHENGYANG N, KRUMBEIN A. Transition transport modeling for the prediction of crossflow transition: AIAA-2016-3572[R]. Reston, VA: AIAA, 2016.

[25] 張坤, 宋文萍. eN方法在無限展長后掠翼邊界層轉捩判斷中的初步應用[J]. 西北工業大學學報, 2011, 29(1): 142-147.

ZHANG K, SONG W P. Application of the full eNtransition method to the infinite swept-wing’s transition prediction[J]. Journal of Northwestern Polytechnical University, 2011, 29(1): 142-147 (in Chinese).

[26] 左歲寒, 楊永, 李棟. 基于線性拋物化穩定性方程的后掠翼邊界層內橫流穩定性研究[J]. 計算物理, 2010, 27(5): 665-670.

ZUO S H, YANG Y, LI D. Investigation on cross-flow instabilities in swept-wing boundary layers with linear parabolized stability equations[J]. Chinese Journal of Computational Physics, 2010, 27(5): 665-670 (in Chinese).

[27] 孫朋朋, 黃章峰. 后掠角對后掠機翼邊界層穩定性及轉捩的影響[J]. 北京航空航天大學學報, 2015, 41(7): 1313-1321.

SUN P P, HUANG Z F. Effect of sweep angle on stability and transition in a swept-wing boundary layer[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(7): 1313-1321 (in Chinese).

[28] 靖振榮, 孫朋朋, 黃章峰. 小攻角對后掠機翼邊界層穩定性及轉捩的影響[J]. 北京航空航天大學學報, 2015, 41(11): 2177-2183.

JING Z R, SUN P P, HUANG Z F. Effect of attack angle on stability and transition in a swept-wing boundary layer[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(11): 2177-2183 (in Chinese).

[29] 黃章峰, 逯學志, 于高通. 機翼邊界層的橫流穩定性分析和轉捩預測[J]. 空氣動力學學報, 2014, 32(1): 14-20.

HUANG Z F, LU X Z, YU G T. Cross-flow instability analysis and transition prediction of airfoil boundary layer[J]. Acta Aerodynamica Sinica, 2014, 32(1): 14-20 (in Chinese).

[30] HAN Z H, CHEN J, ZHU Z, et al. Aerodynamic design of transonic natural-laminar-flow (NLF) wing via surrogate-based global optimization: AIAA-2016-2041[R]. Reston, VA: AIAA, 2016.

[31] 徐家寬, 白俊強, 喬磊, 等. 后掠翼邊界層橫流不穩定轉捩預測模型[J]. 航空動力學報, 2015, 30(4): 927-935.

XU J K, BAI J Q, QIAO L, et al. Prediction model of cross-flow instability transition in swept wing boundary layers[J]. Journal of Aerospace Power, 2015, 30(4): 927-935 (in Chinese).

[32] 徐家寬, 白俊強, 喬磊, 等. 橫流不穩定性轉捩預測模型[J]. 航空學報, 2015, 36(6): 1814-1822.

XU J K, BAI J Q, QIAO L, et al. Transition model for predicting crossflow instabilities[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6): 1814-1822 (in Chinese).

[33] 史亞云, 白俊強, 華俊, 等. 基于當地變量的橫流轉捩預測模型的研究與改進[J]. 航空學報, 2016, 37(3): 780-789.

SHI Y Y, BAI J Q, HUA J, et al. Study and modification of cross-flow induced transition model based on local variables[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(3): 780-789 (in Chinese).

[34] 戚瓊, 韓慶. 基于Spalart-Allmaras-γ-Reθ t轉捩模型的橫流不穩定性轉捩預測方法[J]. 氣體物理, 2016, 1(3): 19-24.

QI Q, HAN Q. Prediction method of cross-flow instabilities-induced transition based on Spalart-Allmaras-γ-Reθ ttransition model[J]. Physics of Gases, 2016, 1(3): 19-24 (in Chinese).

[35] 鞠勝軍, 閻超, 葉志飛.γ-Reθ t-CF轉捩模型在Spalart-Allmaras湍流模型中的推廣及驗證[J]. 航空學報, 2017, 38(4): 120383.

JU S J, YAN C, YE Z F. Genevalization and validation ofγ-Reθ t-CF transition modeling in combination with Spalart-Allmaras turbulence model[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(4): 120383 (in Chinese).

[36] KRUMBEIN A, KRIMMELBEIN N, GRABE C. Streamline-based transition prediction techniques in an unstructured computational fluid dynamics code[J]. AIAA Journal, 2017, 55(5): 1548-1564.

[37] SMITH A M O, GAMBERONI N. Transition, pressure gradient and stability theory[M]. Long Beach: Douglas Aircraft Company, 1956.

[38] INGEN J L V. A suggested semi-empirical method for the calculation of the boundary layer transition region: VTH-74[R]. Delft: Delft University of Technology, 1956.

[39] SONG W P, ZHU Z, YANG H, et al. Laminar flow wing’s optimization design by RANS solver with automatic transition prediction[C]∥28th Congress of the International Council of the Aeronautical Sciences 2012. Stockholm: ICAS Secretariat, 2012: 716-725.

[40] FEY U, EGAMI Y, ENGLER R. High Reynolds number transition detection by means of temperature sensitive paint: AIAA-2006-0514[R]. Reston, VA: AIAA, 2006.

[41] HAN Z H, DENG J, LIU J, et al. Design of laminar supercritical airfoils based on Navier-Stokes equations[C]∥28th Congress of the International Council of the Aeronautical Sciences 2012. Stockholm: ICAS Secretariat, 2012: 706-715.

[42] 喬志德. 自然層流超臨界翼型的設計研究[J]. 流體力學實驗與測量, 1998, 12(4): 23-30.

QIAO Z D. Design of supercritical airfoils with natural laminar flow[J]. Experiments and Measurements in Fluid Mechanics, 1998, 12(4): 23-30 (in Chinese).