基于Karhunen-Loève展開的分布式變體飛行器最優控制方法

龔春林，赤豐華，谷良賢，方海

1.西北工業大學 航天學院 陜西省空天飛行器設計重點實驗室，西安 710072 2.西北工業大學 航天飛行動力學技術重點實驗室，西安 710072

傳統飛行器大都采用固定的外形，設計方案是在多種飛行狀態之間性能折中的結果，難以適應復雜的、具有大飛行包絡的新一代飛行器需求[1]。變體飛行器可以根據飛行狀態和環境變化，動態改變外形以獲得最佳流場，保證大飛行包絡下整體性能最優，對提高飛行器性能具有很大的應用潛力，得到國際飛行器領域廣泛關注。

變體飛行技術發展至今，可大致劃分為集中式和分布式兩類。早期集中式變體技術采用簡單機構實現變后掠、變展長等單個或少數變形自由度，以適應多種飛行任務。雖然集中式變體技術已經在B-1B槍騎兵、F-14雄貓、V-22魚鷹等已服役飛行器中得到應用，并具有結構簡單、可靠、易實現等優點，但變形方式有限，不能對流場進行精細控制，難以適應高動態復雜飛行任務。

近年來，隨著智能材料和結構、微小型驅動器以及分布式控制理論[2]的發展，實現多自由度連續變形的分布式變體技術逐漸得到關注。其采用多個驅動器實現局部或全局的連續變形，可以在很大范圍內快速精細地調整微觀流場，以適應飛行狀態連續動態變化，是未來變形飛行技術的主要發展方向，成為當前研究者們關注的焦點。美國賓夕法尼亞州立大學設計了一種分布式變形結構，通過八面體腱驅動柔順細胞桁架實現變形[3]，如圖1(a)所示。Grumman公司設計了圖1(b)所示的自適應桁架翼肋結構，通過分布式驅動器改變機翼橫截面翼型[4]。南京航空航天大學研制了圖1(c)所示的分布式驅動變形機翼實驗平臺對分布式控制的問題展開研究[5,7-8]。洛克希德·馬丁公司設計了通過響應電脈沖的記憶膜改變機翼形狀的MPUAV。美國DARPA資助NextGen研發了一種滑動蒙皮的變形翼設計方案[9]。楊智春和解江[10]設計了一種應用于變體機翼的柔性后緣自適應機翼。李偉等[11]對變體翼梢小翼的伸縮柵格進行了研究，發現其可對飛機起飛階段的流場進行改善。

圖1 分布式變體結構Fig.1 Distributed morphing structure

變體技術使得飛行器具有更強的靈活性和任務適應性，但也帶來了新的挑戰問題，即面臨動態變化的飛行任務，如何以最優的方式控制飛行器的變形過程。

Falc?o等[12]對NACA0015的可變形翼尖小翼的兩個可變翼型參數進行了優化，獲得了滿足多種高度和速度飛行狀態下的最優解。Holland等[13]采用多學科優化框架，對無人機機翼展長、弦長、后掠角等變形參數在多個典型飛行條件下的飛行性能進行了優化。Dale等[14]利用多學科優化技術針對機翼彎度的變形開展了研究。以上研究的優化問題僅針對少數的典型飛行狀態，如高低空巡航、低速巡邏等，所獲得的一般是“分檔”變形規律，不適用于飛行狀態連續變化的飛行任務。

Vale等[15]利用最優控制理論對兩自由度變形翼(變彎度和變展長)的變體飛機進行了優化。Mir等[16]對變后掠翼無人機變體滑翔軌跡展開最優控制，得到了最優的變體規律。Ryan和Lewis[17]對可變翼炮彈軌跡中的變體規律進行了優化，研究了翼面形狀隨軌跡的規律。嚴旭飛和陳仁良[18]用最優控制方法研究傾轉旋翼機的最優動態傾轉過渡過程，并得到了最優操縱策略。李煥煥[19]針對Z型可折疊翼變形飛行器和可伸縮變后掠翼變形飛行器的不同飛行任務進行了軌跡優化。以上研究雖然考慮了變體飛行器在整個飛行軌跡的最優控制問題，但主要針對包含少數變形自由度的集中式變形技術，不適用于理論上具有無窮變形自由度的分布式變體技術。

在變體飛行器控制方面，很多學者也開展了大量的研究。Nigam等[20]發展了包含子系統辨識和最優控制兩個部分的仿生變體飛行器自適應控制系統。Guo等[21]對仿海鷗翼的變體飛行器，分別采用變體翼和傳統舵進行軌跡和姿態的動態控制。高仁璟等[22]對基于壓電纖維復合薄膜驅動器的變體進行了研究，提出了一種滿足類翼面平板結構的彎曲、扭轉和彎扭型面精確變形控制需求的布局與控制參數協同優化設計方法。董朝陽等[23]對一類存在執行機構故障的分布式結構變體飛行器的控制分配問題，提出一種基于布谷鳥搜索算法的容錯控制方法。但是，目前變體控制研究大都只針對飛行過程中從某一狀態過渡到另一狀態，由于變體導致的動力學模型變化帶來的過渡過程控制問題。

與現有研究相比，本文重點解決在飛行任務連續、動態變化情況下，如何實現分布式變形過程優化問題。該問題本質上是一個變量在時間和空間上均具有無窮維度的優化問題，求解困難在于：① 現有最優控制方法無法直接求解無窮維控制量問題；② 由于變形引起的氣動模型數據和動力學模型維度增加，計算量呈級數增長，優化求解困難。現有研究對該問題涉及較少。

本文第1節給出了變體飛行器動力學通用模型，并給出原始問題的數學模型。第2節針對原問題求解困難，首先采用Karhunen-Loève展開方法對變形域進行空間離散，將其轉化為有限維度控制參數和幾何模態描述，將原問題轉化為有限維度最優控制問題；然后，利用Kriging方法構造了與變形控制參數相關的氣動性能參數代理模型，解決直接采用氣動數值計算方法的計算困難；最后，應用hp偽譜法構造了該最優控制問題的求解過程。第3節針對某翼型可分布式變形的飛行器算例，實現全彈道上翼型隨時間變形規律的優化。

1 分布式變體最優控制問題

分布式變體飛行器的特點是可以實現多自由度連續變形，最優控制的目的是找到最適合當前飛行任務的變形規律，使得其相對某種指標具有最優性。在給出該最優控制問題的求解方法之前，首先考慮變形導致的氣動力作用于飛行器引起飛行軌跡的變化，給出變體飛行器一般動力學模型，在此基礎上提出最優控制問題。

1.1 變體飛行器動力學模型

變體飛行器的飛行概念如圖2所示。不考慮地球旋轉和地球曲率，具有分布式變體特征的飛行器在縱向對稱平面內的動力學模型可統一表示為

(1)

圖2 變體飛行示意圖Fig.2 Morphing procedure during flight

L=qSCL(Ma,y,α,Ω)

D=qSCD(Ma,y,α,Ω)

(2)

式中：q為飛行動壓；S為參考面積；CL、CD分別為升、阻力系數，與飛行狀態(馬赫數Ma、迎角α、高度y)以及變形域Ω相關。

1.2 最優控制問題

飛行器變體的目的是通過改變外形以最優的方式適應飛行環境和完成既定的任務，是一個典型的優化問題。對式(1)所示的動力學模型，該優化問題可描述為

1) 目標函數

根據變體飛行器執行任務的不同，目標函數的選擇不同。但其一般表達式為

(3)

式中：γ(·)和K(·)為與終點條件和過程相關的目標函數；f(t)為運動軌跡；tf為任務結束時刻；u為控制變量。如以燃料消耗最少作為設計指標，則目標可簡化表示為

(4)

2) 控制變量

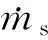
Ω∈[Ωmin,Ωmax]}

(5)

式中：下標max和min分別表示控制變量的上下邊界。對變形函數Ω，其上下邊界由變形執行機構的可達行程和變形結構材料的可變形程度決定。

3) 狀態變量

狀態變量s反映了任意時刻飛行器的狀態，由控制變量決定，可表示為

s={θ∈[θmin,θmax]，x∈[xmin,xmax]，

y∈[ymin,ymax]，m∈[mmin,mmax]，

V∈[Vmin,Vmax]}

(6)

4) 約束模型

變體飛行器在飛行過程中受到動壓q、法向過載ny、起點和終點狀態變量等約束限制。約束變量c表示為

ny=|Lcosα+Dsinα|/(mg)≤nymax,

(7)

式中：ρ為大氣密度；下標0和f分別表示起點和終點條件；上標*表示狀態變量的約束值。

至此，建立起考慮變形函數Ω(t)的分布式變體飛行器的動力學模型和最優控制問題，可表述為：在狀態變量s遵循動力學方程式(1)，以及滿足約束c的前提下，獲得最佳的控制變量隨時間變化規律u*(t)，使得目標函數J最小化。

2 分布式變體最優控制方法

1.2節提出的是一個典型的最優控制問題。由于變形域Ω(t)是曲線或曲面隨時間變化的函數，因此控制變量在空間上具有無窮維度。現有的最優控制問題求解方法包括直接法或間接法，主要針對有限維度控制變量如何進行求解，不能解決無窮維度控制變量的優化問題。本文研究思路是通過構造一種空間上的離散方法，將函數Ω轉換為有限維度變形控制變量描述，從而將原問題轉化為有限維控制變量的最優控制問題。以下將基于Karhunen-Loève(K-L)展開方法[24]進行離散。

相對一般飛行器的最優控制問題，變形控制變量的存在增加了氣動分析的維度，將會使得氣動計算量呈級數增長，給優化問題求解帶來嚴重的計算負擔。本文提出采用Kriging方法構建代理模型解決該問題。

以上兩個問題解決后，可以按照一般最優控制問題處理。本文采用hp自適應偽譜方法進行求解。

2.1 基于K-L展開的變形控制變量離散

對于一個曲面或者曲線，可直接將其離散成有限個控制結點，通過改變控制結點位置來對曲面或曲線進行變形。控制結點數即為可變形的維度。對隨時間變化的曲面,有

Ω(x,y,z;t)=0

(8)

將其離散成s個隨時間變化的坐標結點：

ni(t)∈Ω(x,y,z;t)=0 (9)

每一個結點都是一個獨立的變形維度，其變形過程可以表示為

ni(t)=ni(0)+Δni(t)

(10)

式中：ni(0)為結點i的初始坐標；Δni(t)為結點i在t時刻相對初始坐標的變形量。

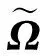
首先將變形量Δni(t)描述為一隨機場量ψ(n,t)，(n,t)表示空間坐標和時間變化，通過將其展開為協方差方程的特征函數(正交函數)的無窮維線性組合[25]，并采用一組基本模態和對應特征值描述該場量，則控制變量數可減少為模態數。

每個節點隨時間的變化可以表示為

Δni(t)=ψi(n,t)·ni

(11)

式中：ni為結點i的單位法向量；ψi(n,t)為變形的隨機場量在i點的分量。

隨機場量ψ(n,t)可表示為

(12)

式中：λ1≥λ2≥…≥λi≥…≥0和zi分別為協方差函數的特征值和特征向量。任意兩離散結點i、j的協方差函數可表示為

(13)

Xi(t)作為非相關隨機變量，均值為0，方差為1。ψ0(n)是隨機場的均值，對于表示變形量的隨機場來說，ψ0(n)=0。

在L∞(Γ)×L2(O)中，若特征值衰減得很快，則可取式(12)中前d項ψd精確表示ψ：

(14)

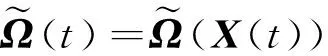
(15)

至此，將原無窮維度的變形函數Ω(t)變化規律轉化為由d維變量控制的變化規律。

以RAE2822翼型外形參數為例，對上述方法進行驗證。將翼型外形離散成192個離散點，選擇前163個離散點進行變形。協方差函數選擇為

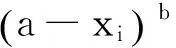
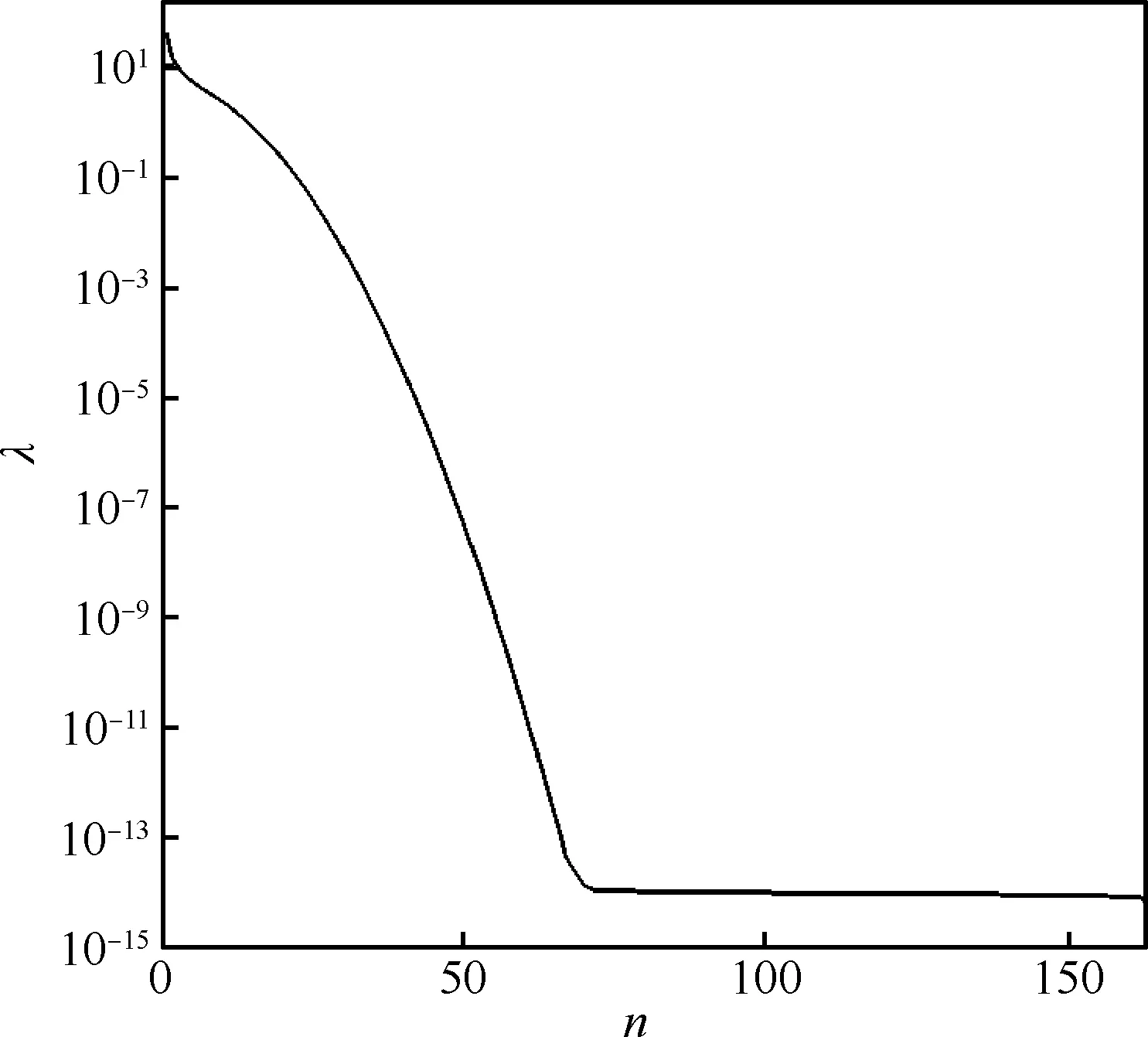
圖3 翼型離散后計算的特征值Fig.3 Eigenvalues of discrete airfoil

圖4 前9個特征值對應的翼型模態Fig.4 Airfoil modalities of the top 9 eigenvalues

2.2 變體飛行器氣動代理模型建立方法

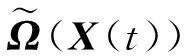
D=qSCD(Ma,y,α,X)

L=qSCL(Ma,y,α,X)

(16)

相對一般飛行器的氣動力模型，由于引入了d個變形控制變量，將會給最優控制問題求解帶來極其嚴重的計算負擔。若在每個變形控制變量取M個點，則插值點的數量增長為非變體飛行器的Md倍。為了解決該問題，本文利用拉丁超立方抽樣(Latin Hypercube Sampling，LHS)[26]和Kriging法[27]結合的方法，建立與變形控制變量相關的氣動代理模型，可以大幅縮減氣動計算維度。所采用步驟如圖5所示。

首先采用LHS方法，在變量X(t)=[X1(t)X2(t) …Xd(t)]組成的試驗空間取N個樣本點X1,X2,…,XN，步驟如下：

步驟1將每個變量i的區間[Xi,min,Xi,max]分為N個子區間，在取樣時以相同概率選擇每個子區間。

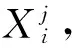
步驟3重復步驟2，直到抽取N個變形控制變量樣本點{X1,X2,…,XN}。

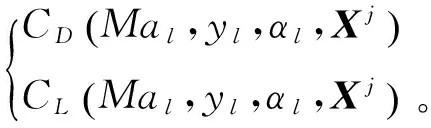
以CD為例，可采用Kriging方法得到任意未采樣點的預測值：

(17)

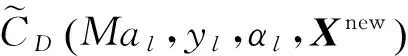
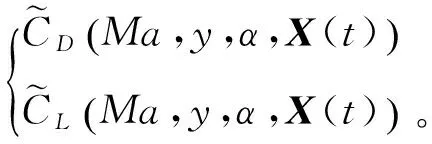
圖5 氣動代理模型建立步驟Fig.5 Steps of aerodynamic surrogate model

2.3 基于hp偽譜方法的最優控制問題求解

通過2.1節的離散，將原最優控制問題轉化為一個有限維度的最優控制問題，可以采用直接法或間接法進行求解。對變體飛行器氣動非線性較強的軌跡優化問題，為了加快求解時的收斂速度，對動力學方程進行無量綱處理。結合2.2節構造的氣動代理模型，最終得到的動力學模型為

(18)

式中：“—”表示該變量的無量綱形式。

考慮到該問題控制變量維度較高，設計空間復雜，選擇直接法中計算性能較高的hp自適應偽譜方法[29-30]。首先在一系列Gauss點上將控制變量u和狀態變量s離散，并以這些離散點為結點構造Lagrange插值多項式來近似控制變量和狀態變量，可將最優控制問題轉化為具有一系列代數約束的參數優化問題，即非線性規劃問題進行求解。對優化算法，選擇計算效率較高的序列二次規劃方法。

2.4 求解流程

綜上，本文研究的分布式變體飛行器最優控制問題求解流程如圖6所示。主要步驟包括：

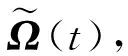
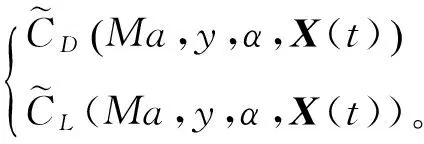
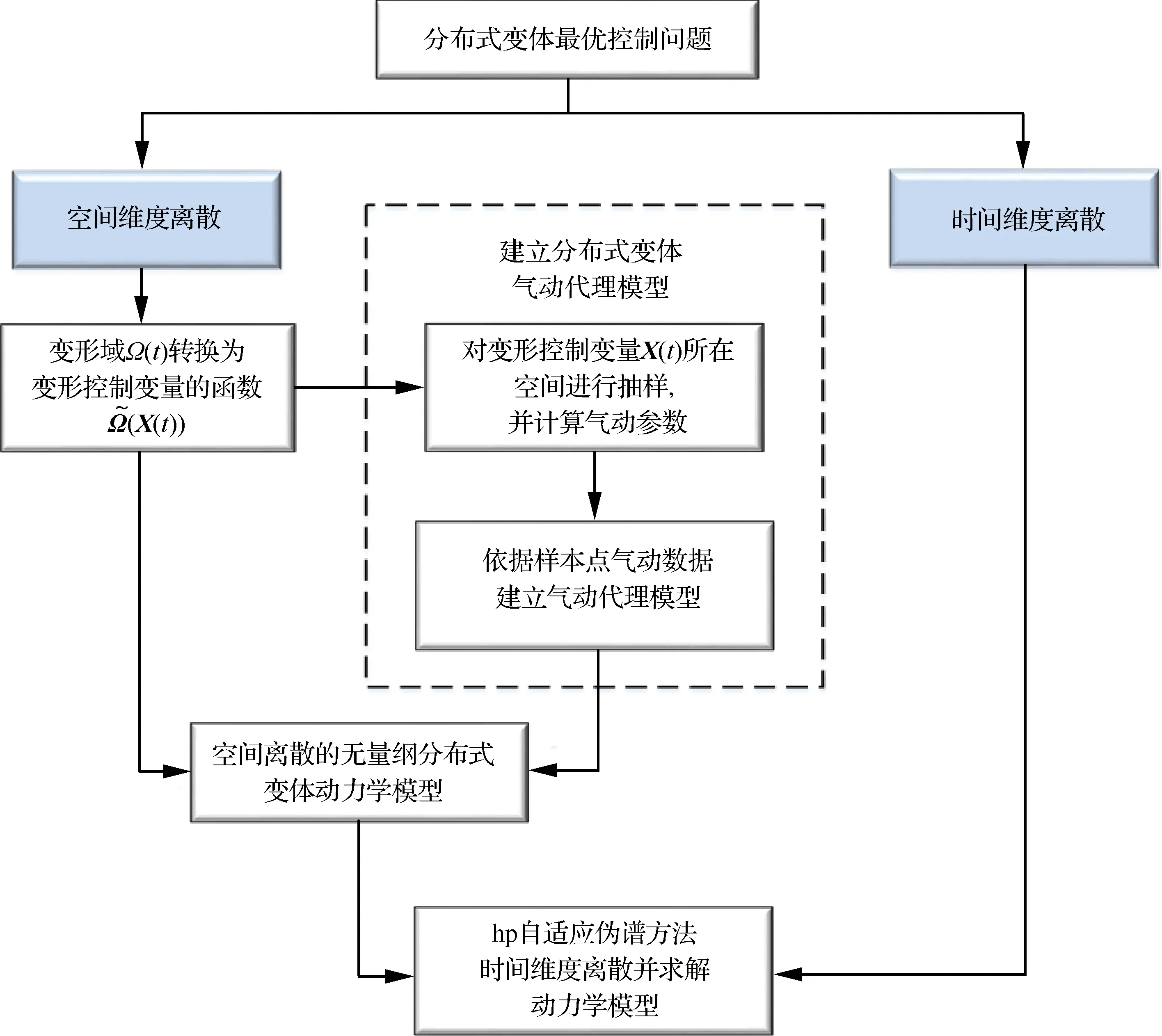
圖6 分布式變體飛行器最優控制問題求解流程Fig.6 Flow chart of solution for optimal control distributed morphing flight vehicle

步驟3采用hp自適應偽譜法，對變形域的參數化模型在時間維度進行離散，對整個飛行軌跡進行一種考慮分布式變體的優化求解，以達到最優的性能(如最小燃料消耗量)。

3 變翼型飛行器算例

假設某變翼型飛行器的翼型采用可分布式變形的RAE2822翼型，翼的平面形狀為平直翼，外形如圖7所示。該算例的任務目標是通過同時控制發動機燃油消耗、迎角以及翼型的變形過程，使得其以最節省的燃油量從給定地點到達指定地點。如圖8所示，飛行器可以有多條飛行軌跡完成這樣的飛行任務，而如何選擇一條最優的軌跡來達到目標參數最優，是一個典型的最優控制問題。

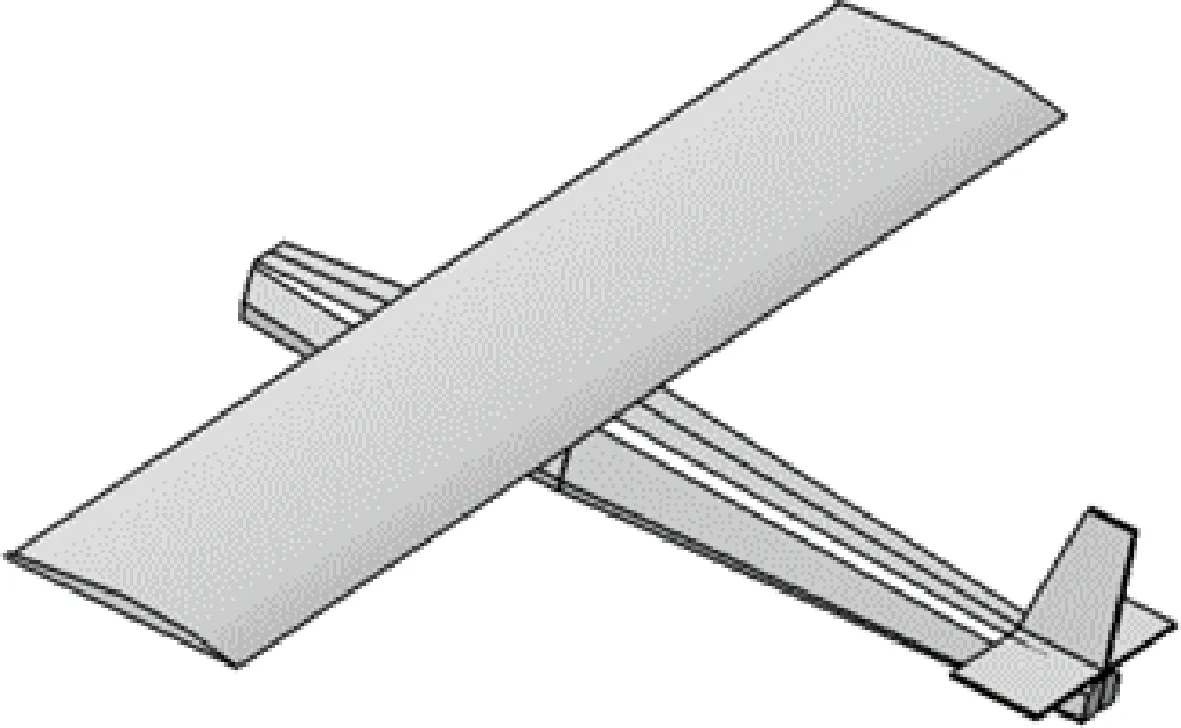
圖7 平直翼變翼型飛行器Fig.7 Morphing airfoil of straight wing aircraft

圖8 變翼型飛行器飛行軌跡規劃Fig.8 Flight path design for morphing airfoil aircraft

算例的主要參數如表1～表3所示。該算例主要用于驗證第2節發展的方法，利用建立的變體飛行器動力學模型，以燃料消耗量作為評價指標，研究在大海拔跨度條件下，利用基于K-L展開的變翼型方法和基于hp自適應偽譜法的最優控制方法對變翼型飛行器性能的提高，并與采用固定翼型飛行器的優化結果進行比較。為了突出主要因素，忽略由于機翼變形引起的機體的升、阻力變化，且假設沒有橫向氣流流動。在優化問題中，飛行器的氣動特性變化主要與翼型的變形相關。

表1 控制變量Table 1 Control parameters

表2 狀態變量Table 2 State parameters

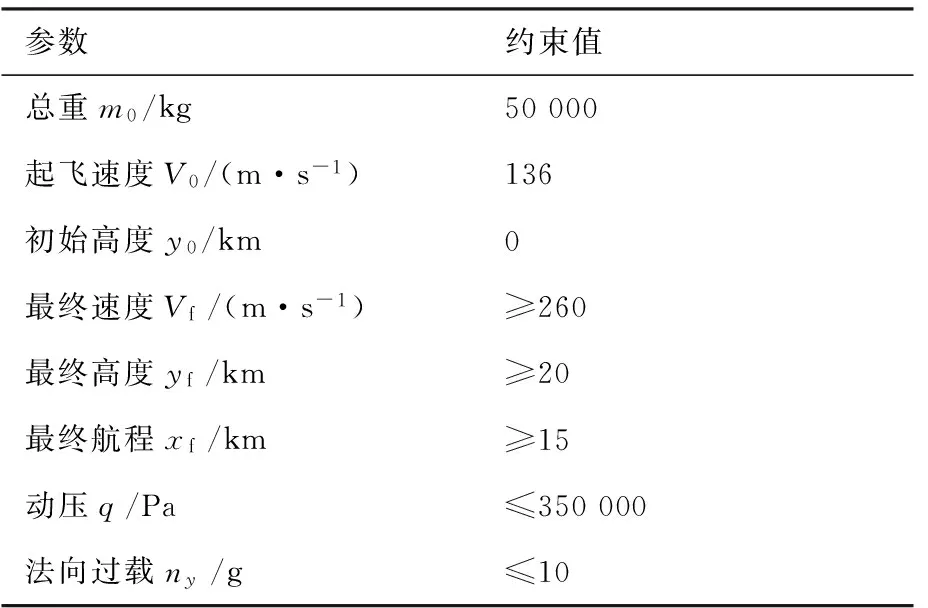
表3 約束模型Table 3 Constraint model

3.1 RAE2822翼型變形描述

為了探究K-L展開應用于翼型變形的效果，如2.1節所述方法，只取前2個特征值和特征向量來表示隨機場ψ，可得

(19)

選取X1(t)、X2(t)作為變形控制變量，以式(19)得到的ψ(n,t)作為變形量，沿著翼型離散點的法線方向變形，即

(xi,yi)new=(xi,yi)old+ψi·ni

(20)

圖9顯示了初始RAE2822翼型和當X1=-0.002、X2=0.006時的變形情況。注意翼型的尾部不發生變形，以此來保證氣動計算時的收斂。

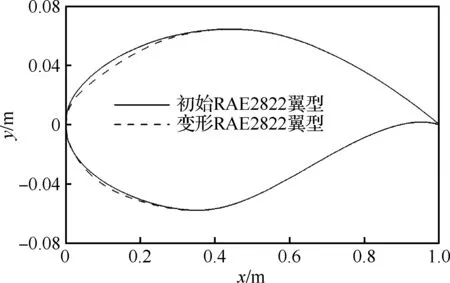
圖9 初始RAE2822和變形后的RAE2822翼型Fig.9 Original and transformed RAE2822 airfoils

3.2 氣動代理模型構造結果

優化過程中，2個變形控制變量的區間取為[-0.006,0.006]。利用LHS方法，抽取N=20個點，抽樣結果如圖10所示。

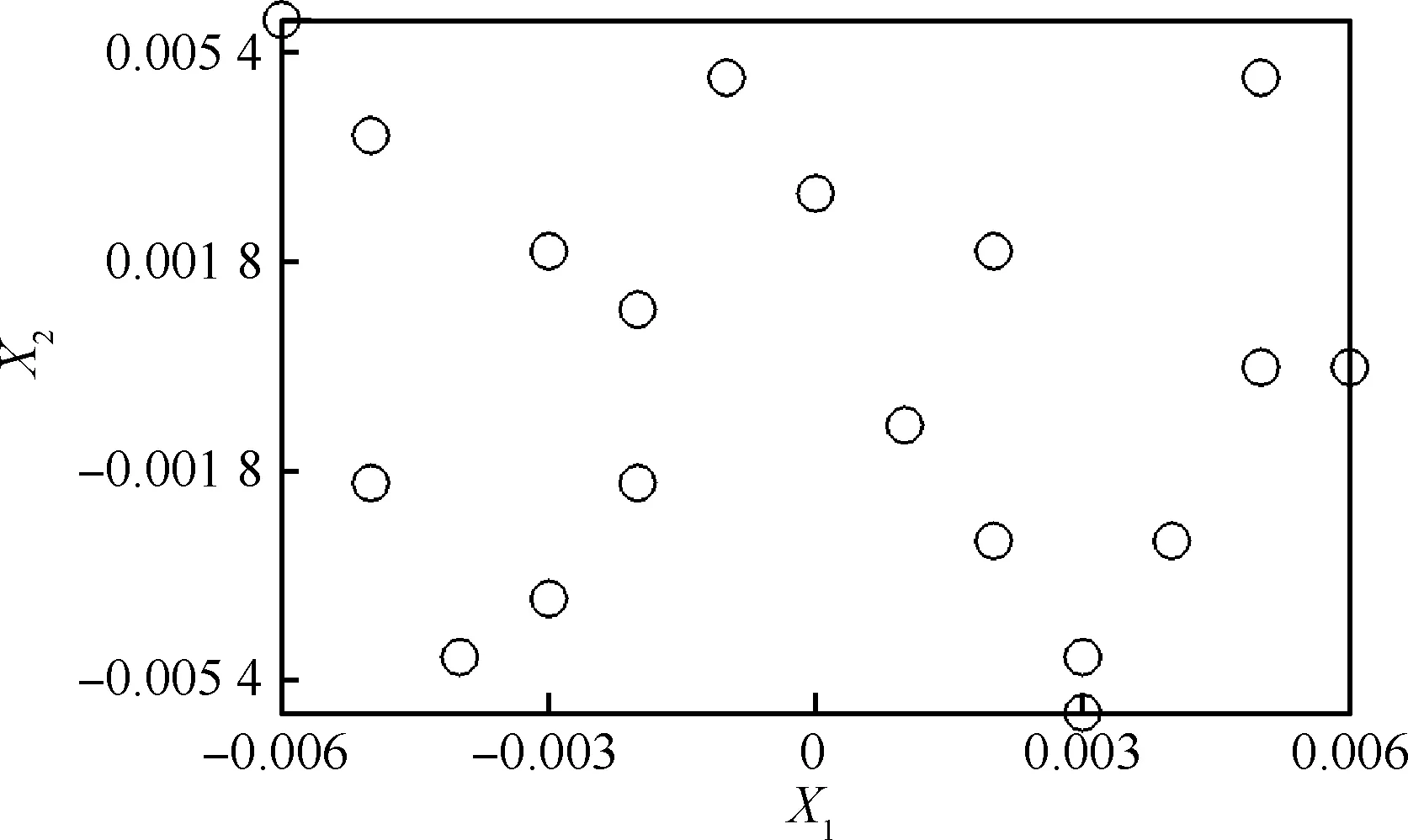
圖10 變形參數LHS結果Fig.10 LHS results of morphing parameters

對初始RAE2822翼型和樣本點上的變形RAE2822翼型，利用CFD計算工具FLUENT計算氣動力系數CD和CL數據庫。計算所用黏流模型為sutherland，湍流模型為SSTk-Ω模型，離散方法為Least Squares Cell Based，二階迎風格式。圖11為RAE2822的2D結構氣動網格。

利用Kriging方法，選用高斯模型作為變異函數模型，選用二階多項式作為回歸模型，建立氣動代理模型，可得到各個飛行狀態下不同變形控制變量(X1(t),X2(t))的氣動代理模型。圖12給出Ma=0.4、飛行高度H=0 km、α=4°時CL的代理模型結果，白色小球表示樣本點。可見，代理模型結果與樣本點吻合得很好。

圖11 RAE2822翼型的2D結構氣動網格Fig.11 2D structured aerodynamic grid of RAE2822 airfoil

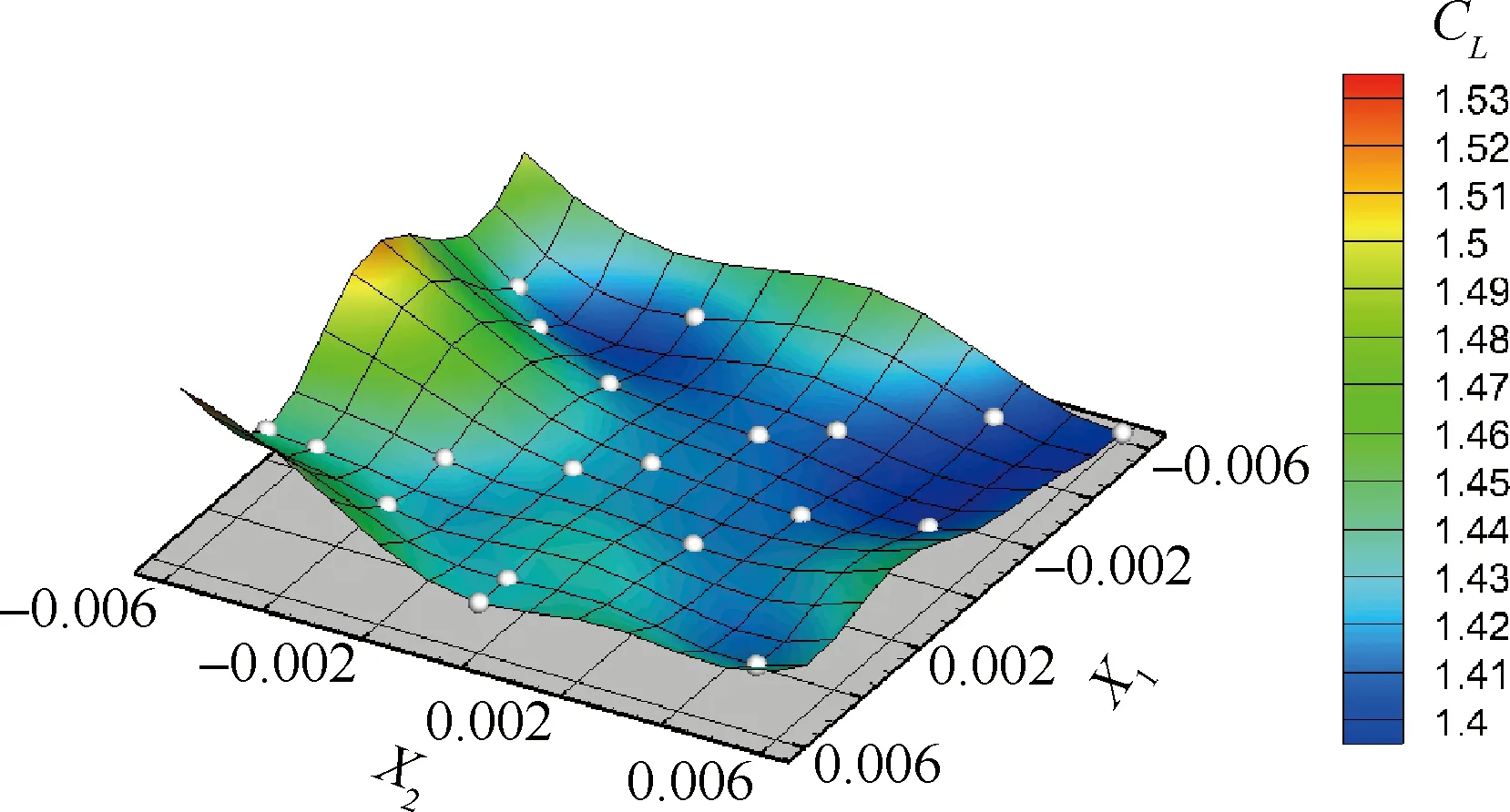
圖12 升力系數代理模型Fig.12 Surrogate model of lift coefficient

3.3 優化結果及分析

利用hp自適應偽譜方法對變翼型飛行器和固定翼型飛行器的軌跡進行優化。圖13和圖14分別給出固定翼型飛行器和變翼型飛行器的控制變量和狀態變量曲線圖。可以看出，利用hp偽譜法得到的彈道優化結果與基于最優控制變量積分的彈道一致，證明了hp方法應用于變體飛行器最優控制的可行性。另外，從優化結果可以看出，變翼型飛行器和固定翼型飛行器優化結果均達到了設計要求，完成飛行任務目標的時間分別為75.7 s和72.5 s。

從圖15和圖16可以看出，在整個飛行過程中，變翼型飛行器的速度比固定翼型飛行器的速度慢，迎角也較小，且沒有達到8°的上界，變翼型飛行器在較小速度和較小迎角的條件下，依然可以完成飛行任務。可見，變翼型飛行器的升力有所提高，采用較小的迎角即可完成給定任務，從而減小了飛行器的阻力。圖17顯示變翼型飛行器和固定翼型飛行器最終的質量分別為43 000 kg和42 801 kg。變翼型飛行器燃料消耗比固定翼型飛行器節省了2.76%。

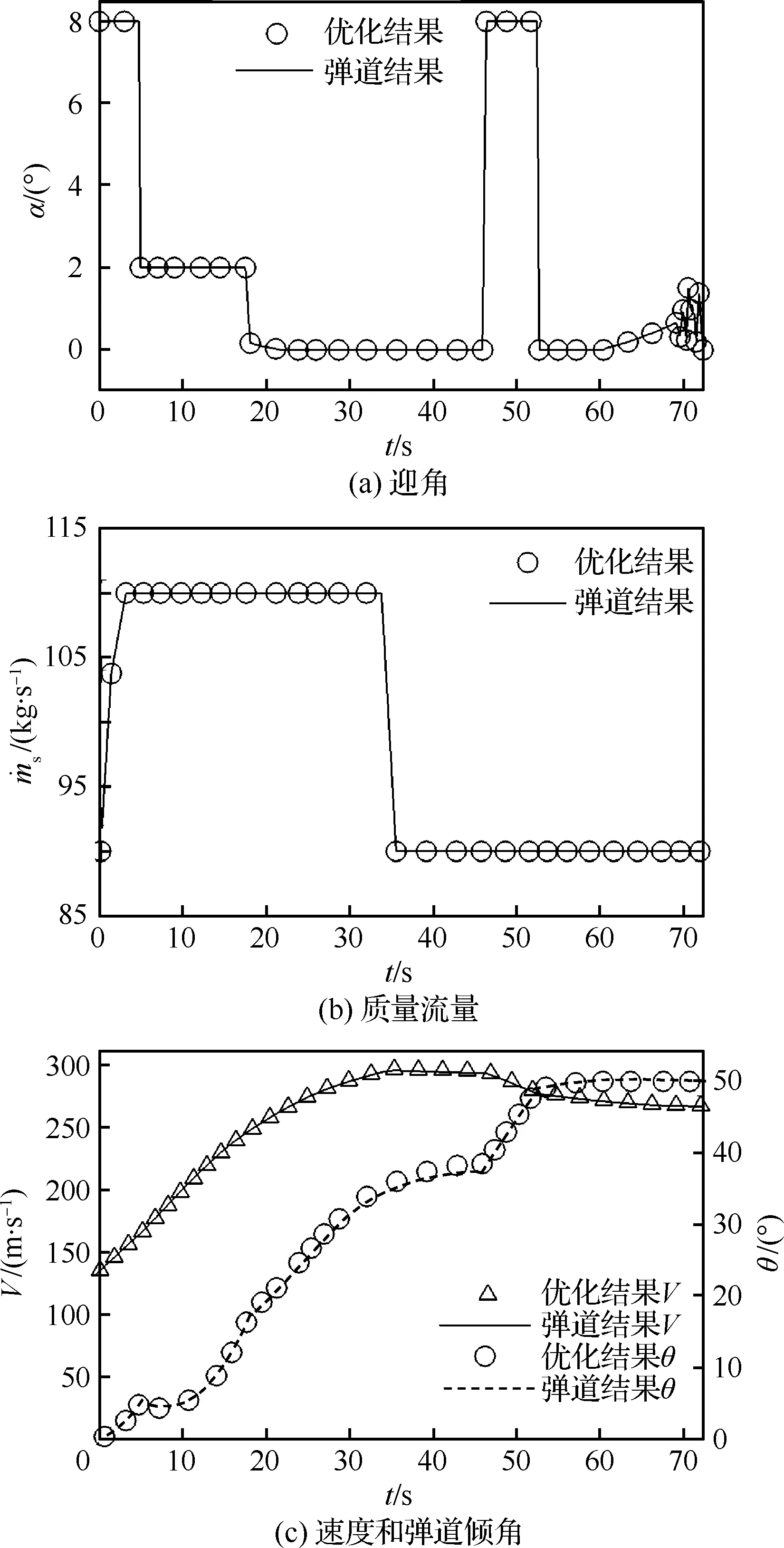
圖13 固定翼型飛行器控制變量和狀態變量優化結果Fig.13 Optimization results of control and state variables of fixed airfoil aircraft

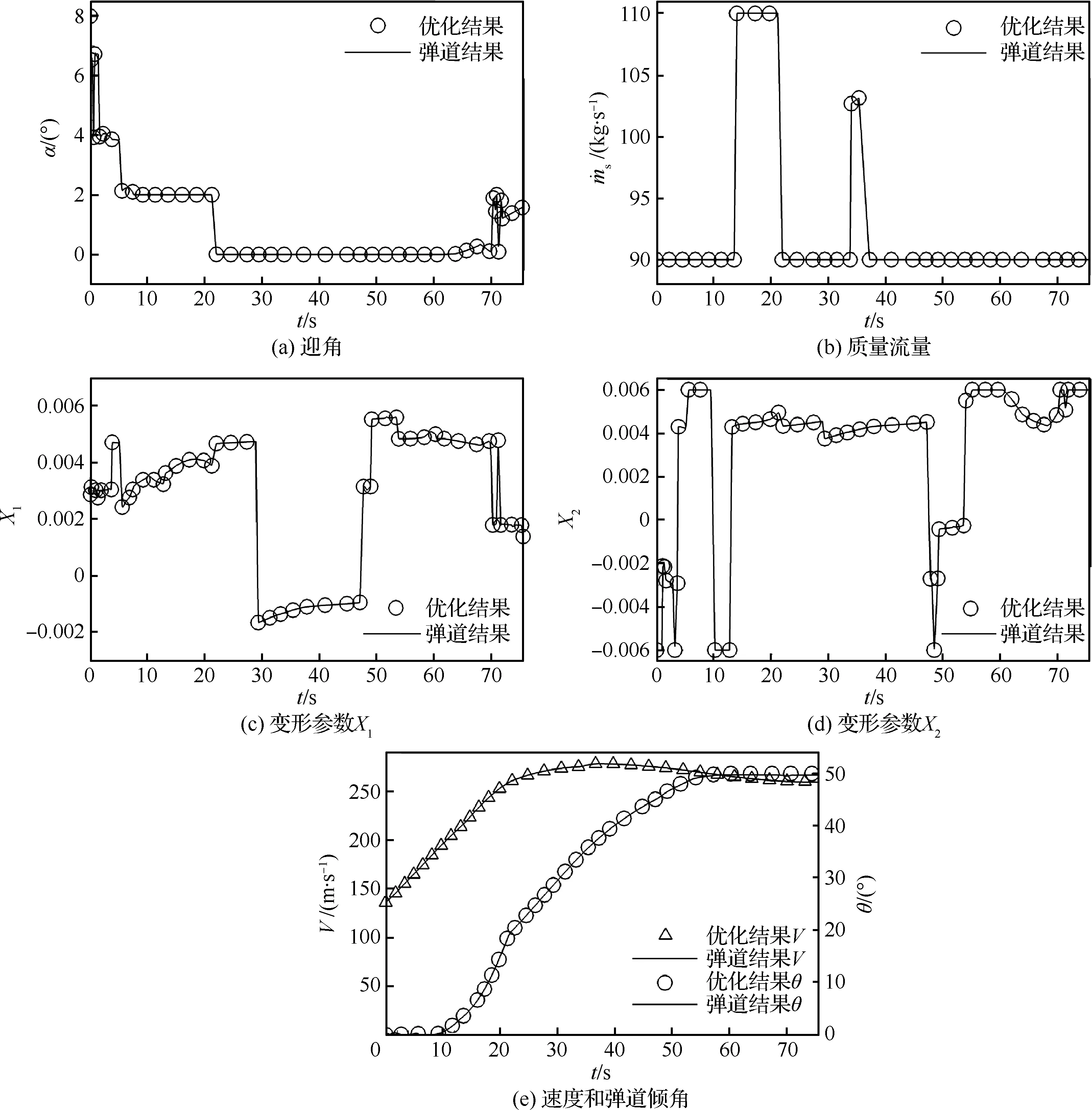
圖14 變翼型飛行器控制變量和狀態變量優化結果Fig.14 Optimization results of control and state variables of morphing airfoil aircraft

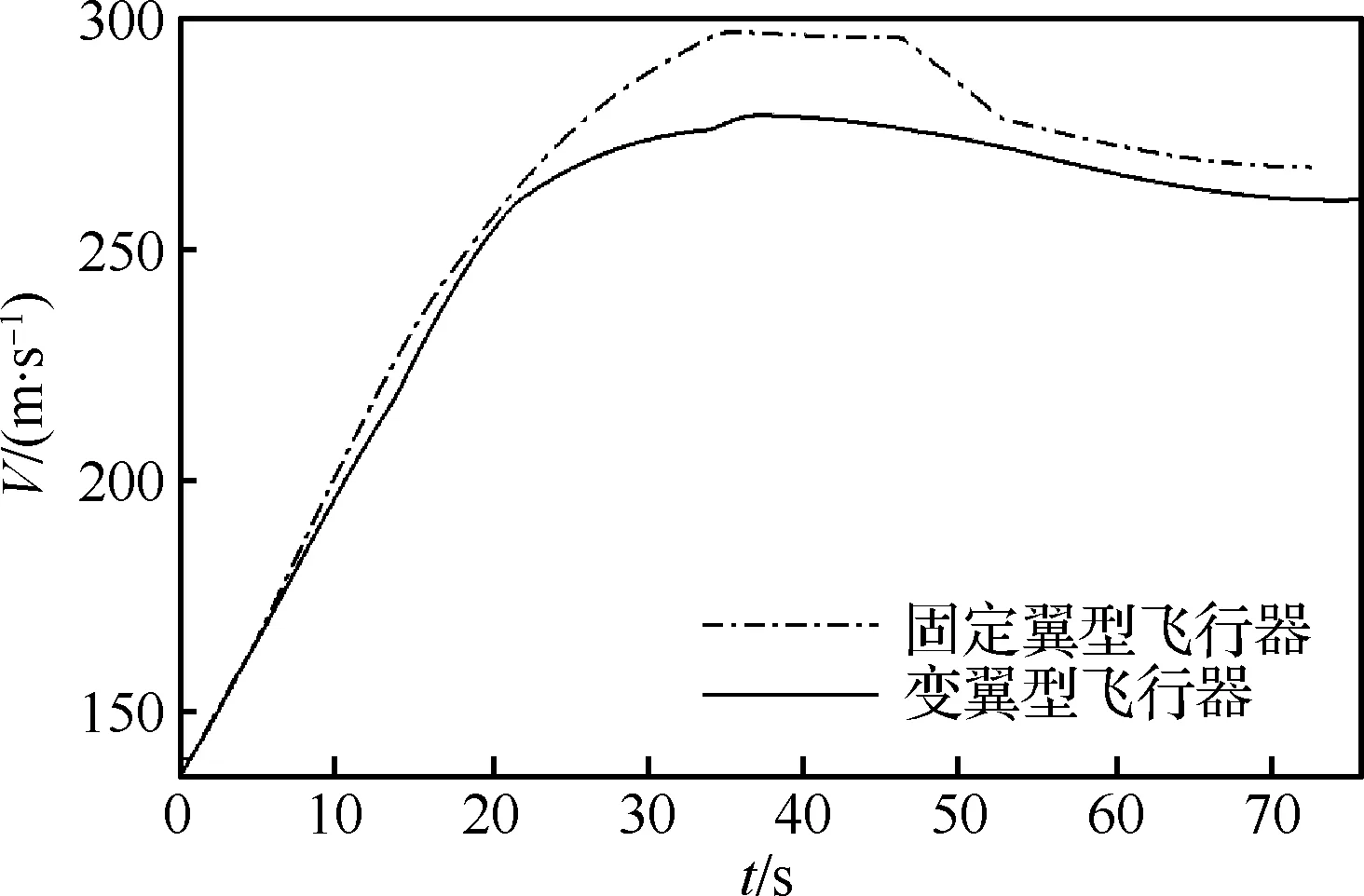
圖15 變翼型與固定翼型飛行器速度對比Fig.15 Comparison of velocities of morphing airfoil aircraft and fixed airfoil aircraft

圖16 變翼型與固定翼型飛行器迎角對比Fig.16 Comparison of angles of attack of morphing airfoil aircraft and fixed airfoil aircraft

從圖18可以看出，在飛行初始階段，由于和固定翼型飛行器相比，變翼型飛行器發動機質量流量較小，導致推力較小，且變翼型飛行器速度和迎角較小，故其彈道高度在飛行初始階段較固定翼型飛行器彈道高度低，如圖19所示。而由于變翼型飛行器改善了不同飛行條件下的升阻力，變翼型飛行器在飛行任務后半段上升速度較快，僅比固定翼型飛行器的飛行時間超出3.2 s即完成了飛行任務。

圖20給出在不同飛行階段最優翼型與固定翼型的對比，c為弦長，h為厚度。雖然在本算例中，由于變形控制變量的變化范圍較小，翼型的可變形范圍也較小，但依然減小了飛行器的燃料消耗量。

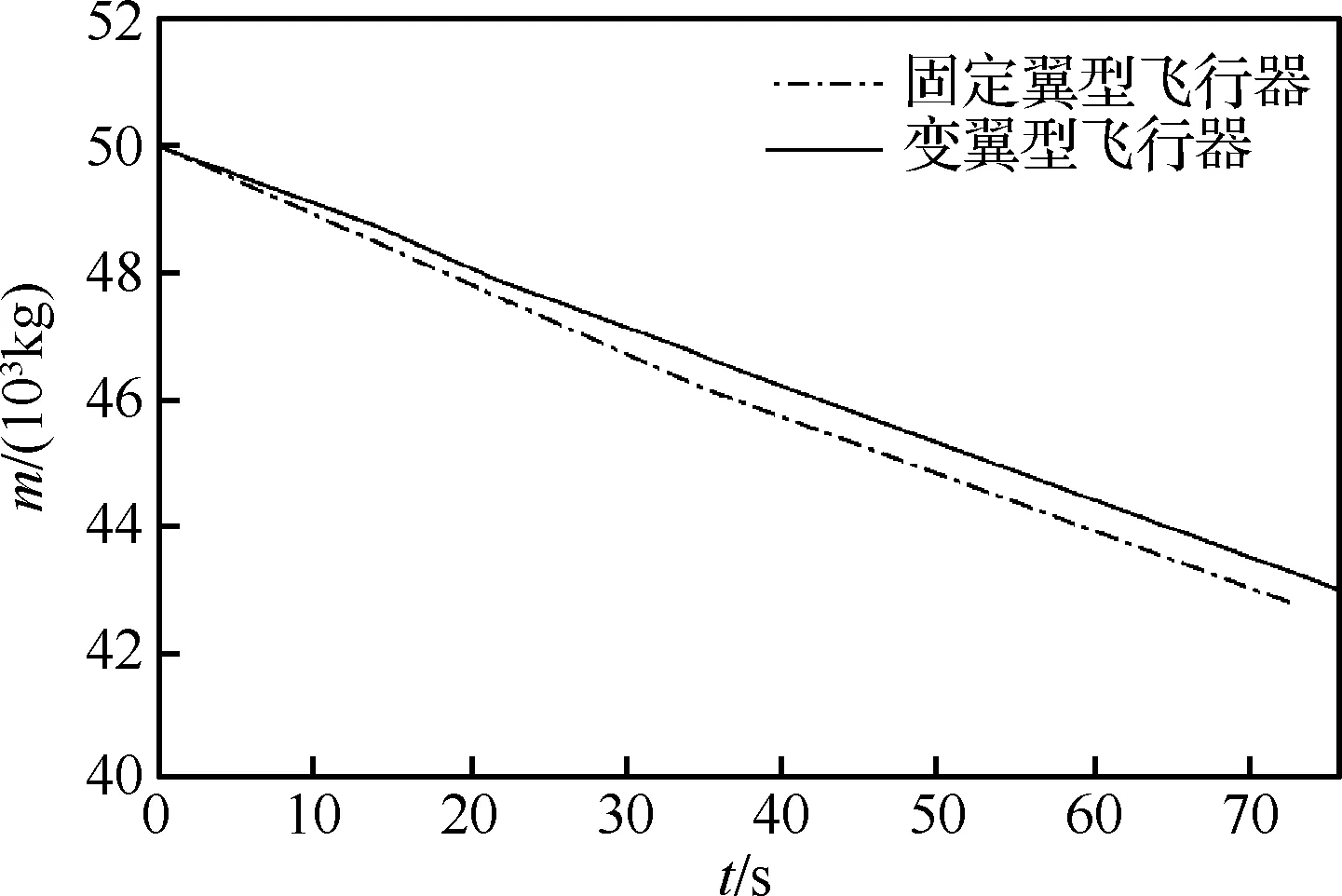
圖17 變翼型與固定翼型飛行器質量對比Fig.17 Comparison of masses of morphing airfoil aircraft and fixed airfoil aircraft

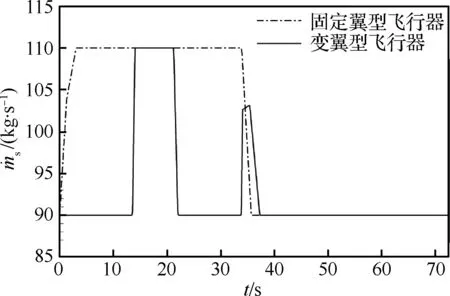
圖18 變翼型與固定翼型飛行器質量流量對比Fig.18 Comparison of mass flow rates of morphing airfoil aircraft and fixed airfoil aircraft

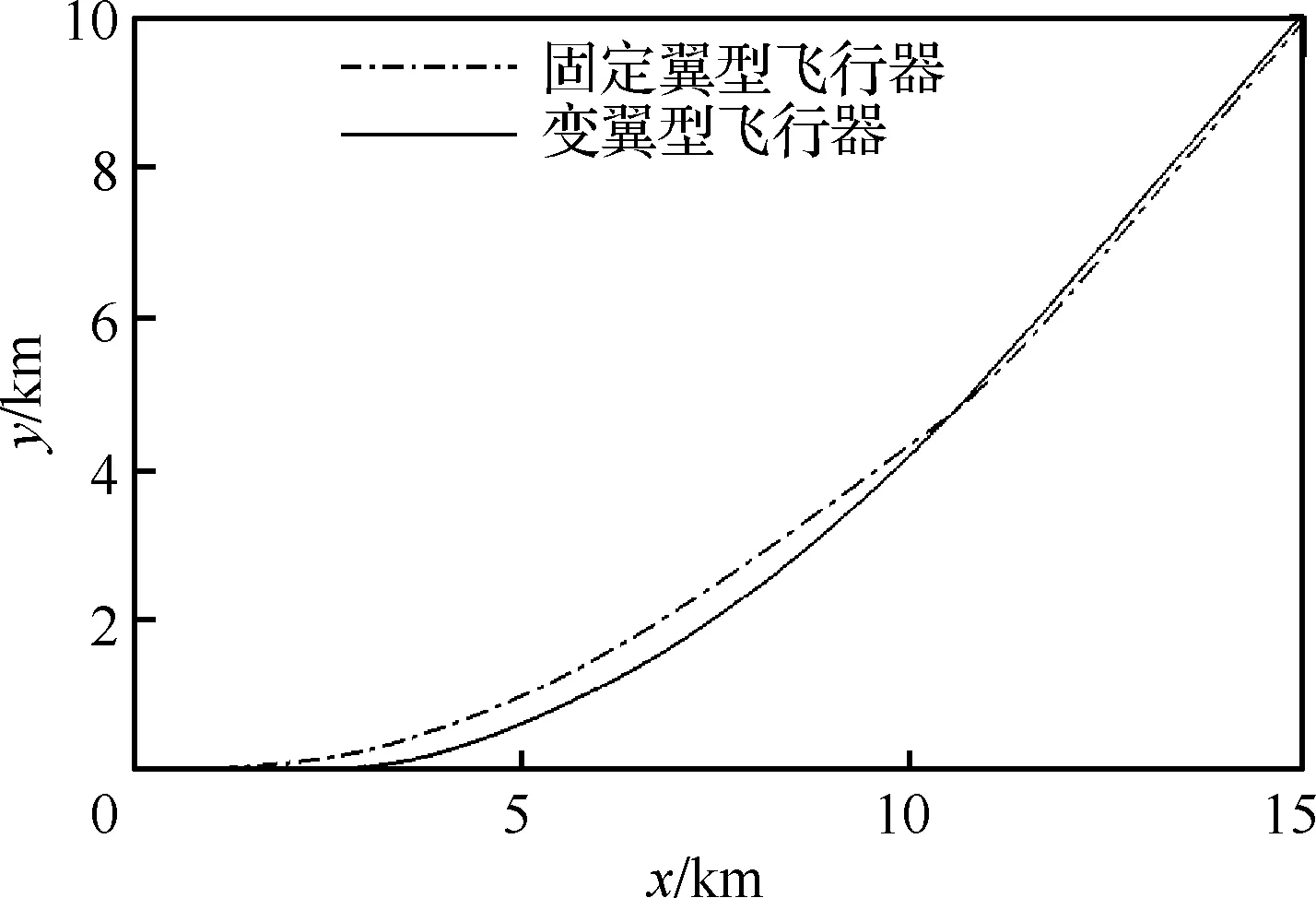
圖19 變翼型與固定翼型飛行器縱向對稱平面彈道對比Fig.19 Comparison of trajectories of morphing airfoil aircraft and fixed airfoil aircraft of longitudinal symmetry plane

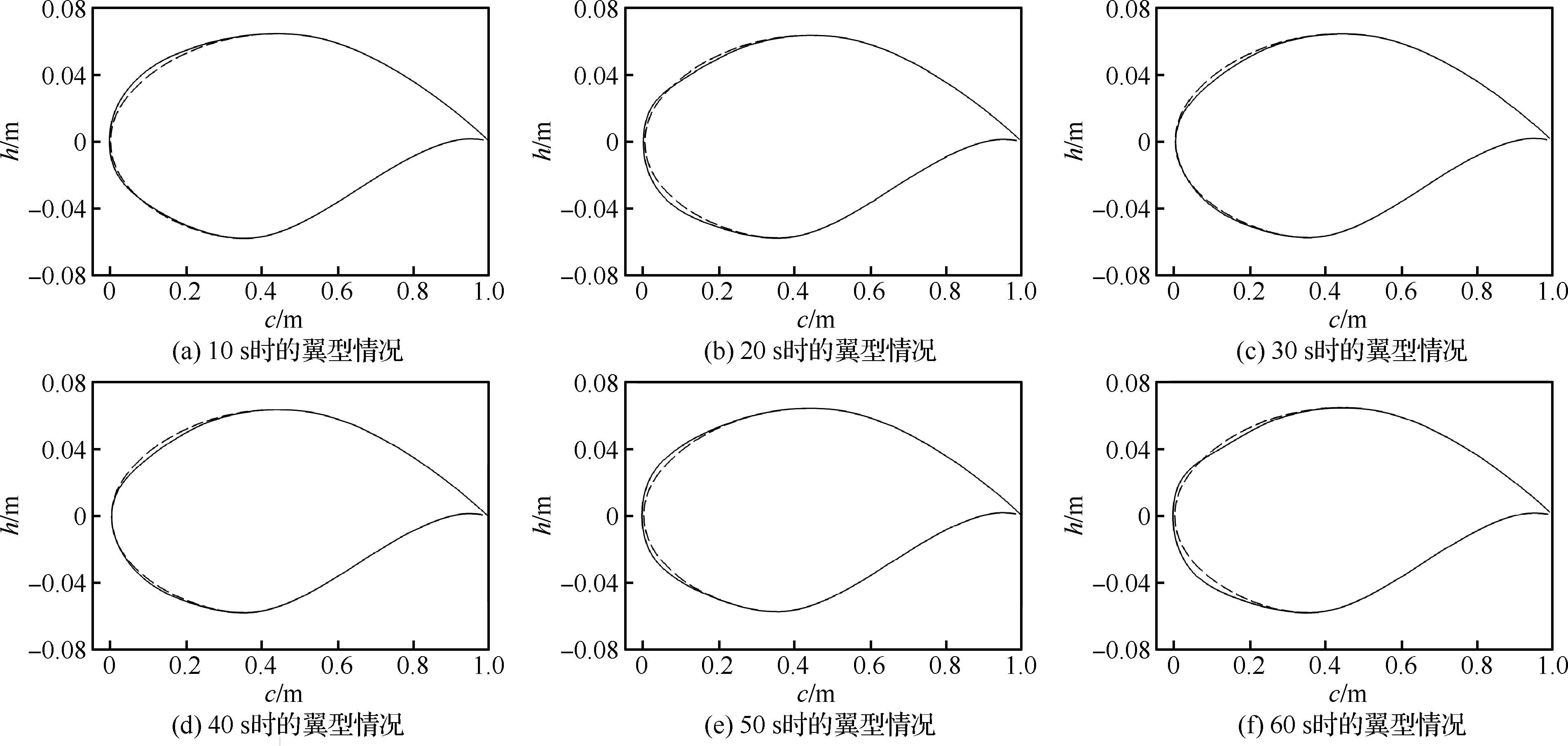
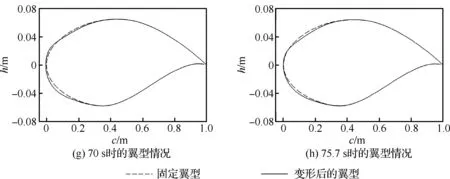
圖20 變翼型飛行器翼型隨時間變化Fig.20 History of airfoils of morphing airfoil aircraft during whole trajectory

4 結 論

隨著智能材料和驅動技術的發展，分布式變體飛行技術的實現和應用已經逐漸成為可能。但其帶來更高飛行性能的同時，也給飛行器帶來了如何進行多維度控制的新問題。本文針對分布式變形規律設計問題，在建立的變體飛行器動力學模型的基礎上，提出了一種最優控制方法。利用Karhunen-Loève展開對分布式變體飛行器變形域進行展開，將空間無限維的變形域轉換為少數變形控制變量的變化規律；結合拉丁超立方抽樣(LHS)和Kriging方法建立了分布式變體飛行器的氣動代理模型，解決了控制變量維度增加帶來的氣動計算問題；在時間維度上，利用hp自適應偽譜方法對參數化的變形域進行離散，并對飛行軌跡進行最優控制。最后以分布式變翼型飛行器為例，利用所建立的求解方法對其飛行軌跡進行優化，達到了最小燃料消耗量的優化目的，驗證了本文方法的有效性。

1) 采用基于Karhunen-Loève展開的變形控制變量離散，可以通過較少的變形控制變量對所有離散結點進行變形，使其變形范圍不僅僅局限于幾種構型，每一個參數化結點坐標都可以變化，具有了更大的自由度。隨著變形域離散結點增多，可以向更大范圍的變形設計空間發展。

2) 所建立的變體飛行器氣動代理模型，僅需較少的樣本點就能夠擬合整個設計空間的氣動參數，顯著降低了計算成本。

3) 對變翼型飛行器與固定翼型飛行器的最優控制問題進行了分析，對比結果顯示采用通過分布式變翼型最優控制，能以較小的速度和迎角完成同樣的飛行任務，減少了2.76%的燃料消耗量。

本文建立的方法對分布式變體飛行器具有共性，能擴展到機體/彈體等更為復雜的變體形式，為未來變體飛行技術發展提供參考和支持。由于目前所采用的算例主要是為了驗證方法的可行性，因此選擇的變形控制變量較少，且變形控制變量約束范圍較小，優化對飛行性能的提升較為有限。在實際工程應用中，為了更精確地表示分布式變形的特點，應選取更多特征值來表示整個變形域的參數化模型，以提高變形自由度，使其在滿足計算成本約束的前提下，最大程度地發揮變體飛行的優勢。另外，現有變形方法對大變形量的處理還存在一定問題，限制了變體對飛行性能的提高，需要進一步改進變形方法。

[1] 杜廈, 昂海松. 改變飛機變體機翼優化方法與氣動特性仿真[J]. 計算機仿真, 2013, 30(3): 88-91.

DU X, ANG H S. Optimization method and aerodynamic character simulation of morphing wing[J]. Computer Simulation, 2013, 30(3):88-91(in Chinese).

[2] KEULEN B V.H∞-control for distributed parameter systems: A state-space approach [M]. Boston，MA：Birkh?user Boston, 1993:101-129.

[3] RAMRAKHYANI D S, LESIEUTRE G A, FRECKER M I, et al. Aircraft structural morphing using tendon-actuated compliant cellular trusses[C]∥Morphing Aircraft Structures Using Tendon Actuated Compliant Cellular truss, 2005:1615-1621.

[4] AUSTIN A F, NOSTRAND W C V. Shape control of an adaptive wing for transonic drag reduction [J]. Smart Materials and Structures, 1995, 2447:45-50.

[5] 文哲遠. 分布式驅動變體飛行器控制的仿真系統研究[D]. 南京：南京航空航天大學, 2012:11-21.

WEN Z Y. Research on simulation system of distributed driven morphing aircraft control [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012:11-21(in Chinese).

[6] 何真. 變體飛行器基礎控制問題研究[D]. 南京：南京航空航天大學, 2009:77-95.

HE Z. Research on basic control problem of morphing aircraft [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009:77-95 (in Chinese).

[7] 吳俊. 變形翼分布式協同控制技術研究[D]. 南京：南京航空航天大學, 2011:82-93.

WU J. Research on distributed coordinated control technology of morphing wing[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011:82-93 (in Chinese).

[8] 陸宇平, 何真. 變體飛行器控制系統綜述[J]. 航空學報, 2009, 30(10):1906-1911.

LU Y P, HE Z. A survey of morphing aircraft control systems[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(10):1906-1911(in Chinese).

[9] RODRIGUEZ A. Morphing aircraft technology survey[C]∥AIAA Aerospace Sciences Meeting and Exhibit. Reston, VA: AIAA, 2013:1-6.

[10] 楊智春, 解江. 柔性后緣自適應機翼的概念設計[J]. 航空學報, 2009, 30(6):1028-1034.

YANG Z C, XIE J. Concept design of adaptive wing with flexible trailing edge[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(6):1028-1034(in Chinese).

[11] 李偉, 熊克, 陳宏,等. 用于變體翼梢小翼的伸縮柵格研究[J]. 航空學報, 2011, 32(10):1796-1805.

LI W, XIONG K, CHEN H, et al. Research of retractable grid applied to morphing winglet[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(10):1796-1805(in Chinese).

[13] HOLLAND M, MOORE B, FERGUSON S. 'Transforming' for stability and aerodynamic performance in a reconfigurable UAV[C]∥12th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference and 14th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. Reston, VA: AIAA, 2012.

[14] DALE A, COOPER J E, MOSQUERA A. Adaptive camber-morphing wing using 0-υ honeycomb[C]∥AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston, VA: AIAA, 2013.

[15] VALE J, LAU F, SULEMAN A. Optimal control and energy balance evaluation of a morphing aircraft[C]∥AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston, VA: AIAA, 2013.

[16] MIR I, MAQSOOD A, AKHTAR S. Optimization of dynamic soaring maneuvers for a morphing capable UAV[C]∥AIAA SciTech Forum. Reston, VA: AIAA, 2017.

[17] RYAN K, LEWIS M. Trajectory optimization studies of long range morphing projectiles[C]∥AIAA Atmospheric Flight Mechanics Conference. Reston, VA: AIAA, 2012.

[18] 嚴旭飛, 陳仁良. 傾轉旋翼機動態傾轉過渡過程的操縱策略優化[J]. 航空學報, 2017, 38(7): 720865.

YAN X F, CHEN R L. Control strategy optimization of dynamic conversion procedure of tilt-rotor aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(7): 720865(in Chinese).

[19] 李煥煥. 新概念變形飛行器飛行軌跡優化設計[D]. 哈爾濱： 哈爾濱工業大學, 2015:38-53.

LI H H. Optimal flight trajectory design of new concept morphing aircraft[D]. Harbin：Harbin Institute of Technology，2015:38-53 (in Chinese).

[20] NIGAM N, ZHANG Y, CHEN P, et al. Adaptive control and actuation system development for biomimetic morphing[C]∥AIAA/AHS Adaptive Structures Conference. Reston, VA: AIAA, 2015.

[21] GUO T, HOU Z, ZHU B. Dynamic modelling and active morphing trajectory-attitude separation control approach for gull-wing aircraft[J]. IEEE Access, 2017, 5:17006-17019.

[22] 高仁璟, 張瑩, 趙劍,等. 面向結構形狀控制的壓電纖維復合薄膜驅動器布局方式與控制參數協同優化設計[J]. 機械工程學報, 2016, 52(18):177-183.

GAO R J, ZHANG Y, ZHAO J, et al. Integrated design optimization of MFC-layout form and control parameters for morphing structural shapes[J]. Journal of Mechanical Engineering, 2016, 52(18):177-183(in Chinese).

[23] 董朝陽, 路遙, 江未來,等. 基于布谷鳥搜索算法的一類變體飛行器容錯控制[J]. 航空學報, 2015, 36(6):2047-2054.

DONG Z Y, LU Y, JIANG W L, et al. Fault tolerant control based on cuckoo search algorithm for a class of morphing aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6):2047-2054(in Chinese).

[24] FUKUNAGA K, KOONTZ W L G. Application of the Karhunen-Loève expansion to feature selection and ordering[J]. IEEE Transactions on Computers, 1970, C-19(4):311-318.

[25] SCHILLINGS C, SCHULZ V. On the influence of robustness measures on shape optimization with stochastic uncertainties[J]. Optimization and Engineering, 2015, 16(2):1-40.

[26] 方開泰. 均勻試驗設計的理論、方法和應用——歷史回顧[J]. 數理統計與管理, 2004, 23(3):69-80.

FANG K T. Theory, method and application of uniform experimental design—History review[J]. Journal of Applied Statistics and Management, 2004, 23(3):69-80(in Chinese).

[27] KRIGE D G. A statistical approach to some basic mine valuation problems on the witwatersrand[J]. Operational Research Quarterly, 1953, 4(1):18.

[28] 李新，程國棟，盧玲.空間內插方法比較[J]. 地球科學進展, 2000, 15(3):260-265.

LI X, CHENG G D, LU L. The comparison of spatial interpolation methods[J]. Advances in Earth Science, 2000, 15(3):260-265(in Chinese).

[29] GANDHI M. Trajectory optimization algorithm studies[J]. Mathematics, 2015, 15(2):267-281.

[30] 張博淵, 宗群, 魯瀚辰,等. 基于hp自適應偽譜法的四旋翼無人機編隊軌跡優化[J]. 科技導報, 2017, 35(7):69-76.

ZHANG B Y， ZONG Q， LU H C , et al. Trajectory optimization of quad-rotor uav formation using hp-adaptive pseudospectral method [J]. Scientia Technologica Sinica, 2017, 35(7):69-76(in Chinese).