航天器捷聯慣組基座構型設計

周劍波，蔡毅鵬，孫學麒，王 亮

(1 中國運載火箭技術研究院， 北京 100076； 2.南京航空航天大學航空宇航學院， 南京 210016)

捷聯慣組基座作為航天器導航與控制系統的關鍵單機——慣組(慣性測量組合)的安裝基座(支架)，其動態特性(主要指對激勵的響應和傳遞特性)直接影響到慣組動態特性，進而影響到慣組力學環境適應性、慣組動態導航精度和航天器的彈性穩定性設計，涉及到力學環境、結構、控制、制導等多個專業，影響范圍廣，設計難度大，在航天器研制中占有重要地位，選擇恰當的基座構型是航天器結構設計的重要內容。

在慣組研制中，人們對動態環境對慣組導航精度的影響模式及誤差補償進行了大量研究[1-7]，對慣組的減振、隔振問題也進行了探討[8-19]，但綜合考慮各方面約束的慣組基座動態特性設計問題研究的公開報道還不多見[18-19]。本文從捷聯慣組基座的設計約束分析出發，對影響慣組基座動態特性的因素進行了討論，對五種典型構型進行了計算和對比分析，提出了關于捷聯慣組基座構型選取的建議。

1 捷聯慣組基座動態特性設計

1.1 捷聯慣組和慣組小系統

捷聯式慣組是將慣性敏感元件(陀螺儀和加速度計)直接安裝在運載體上，不需要穩定平臺，經控制計算機解算(數字平臺)獲得運載體的線運動和角運動[1]。

慣組基座作為慣組的安裝支架，通常由金屬或復合材料制成，構型為梁或板，其本身是彈性體，外界激勵首先作用到慣組基座上再傳遞到慣組上，基座自身動態特性直接影響到慣組的動態特性。由于其重要性和相互間的緊密聯系，航天器設計中將慣組、慣組基座和減振器組成的集合專門稱之為慣組小系統。

1.2 設計約束分析

速率捷聯慣組同時為航天器控制系統的制導系統和姿控系統服務，制導系統和姿控系統對慣組的使用要求有所不同，即：制導系統將慣組作為慣性平臺使用，解算獲取航天器位置信息，姿控系統將慣組作為速率陀螺使用，獲取航天器的姿態信息[1-2]。

捷聯慣組的連接方式決定了慣組電子設備承受較為惡劣力學環境的能力。慣組電子設備對力學環境適應性，即慣組部件的力學環境適應性，主要包括：慣性敏感元件陀螺和速度計(特別是撓性陀螺和石英撓性速度計)，不能讓其承受較大的振動和沖擊；激光慣組的激光陀螺若采用機抖陀螺，則機抖頻率處振動值不能超過額定值；慣組電路板具有抗振動、沖擊、過載能力[1]。

從導航性能分析，力學環境特別是振動會使慣組輸出含有高頻成分。相對于載體的剛體運動，高頻成分是虛假的運動，有可能引起圓錐運動等效應，導致慣組的導航精度降低。因此需要抑制振動(包括線振動和角振動)、沖擊等各種因素引起的誤差，在設計上采取相應措施[3-22]。

為改善慣組的力學環境適應性，滿足動態環境下慣組導航精度要求，捷聯慣組采用減振設計。由于姿控系統需采用慣組陀螺準確感知航天器的姿態信息，從航天器慣組陀螺測角分析，彈體產生彎曲變形后，慣組敏感到的姿態角如圖1所示[2]。

圖1中，a點為慣組安裝位置。彈體偏轉角為Δφ，慣組敏感角度為Δφg。將彈體視為剛體時，慣組的測量方程為：

Δφg=Δφ

(1)

在考慮彈體的彈性變形后，由圖1可以看到，慣組的敏感角中多了一項由于彈性變形引起的附加轉角，航天器剛體測量方程變為：

(2)

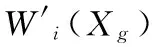
彈性變形引起的附加轉角又包括航天器整體的附加轉角(整體模態)和包括慣組基座局部彈性變形、減振器環節引起的附加轉角(局部模態)，即：

(3)

圖2所示的土星V火箭陀螺安裝支架附加轉角為局部模態造成的附加轉角典型示例。

因此，慣組基座的彈性和減振設計使得捷聯慣組與航天器不是在所有頻段上都是剛性連接，需要對慣組系統的傳遞特性進行限制，主要是角運動傳遞特性(幅頻和相頻)進行限制。

1.3 二自由度分析模型

慣組基座、減振器設計基礎均須分析結構彈性對慣組小系統的影響，即分析慣組小系統在線振動和角振動輸入下的響應和傳遞特性。不失一般性，可建立原型為兩軸車輛減振的二自由度模型[20]，如圖3所示。

設基礎激勵線位移為u，角位移為φ，減振對象(一般為慣組儀表組合體)與減振環節(基座與減振器等效環節)連接點位移為x1和x2，減振對象質心為x，繞質心轉角為θ。減振對象質量為m，相對質心回轉半徑為lI，減振器剛度分別為k1和k2，阻尼系數分別為c1和c2，引入參數[20]：

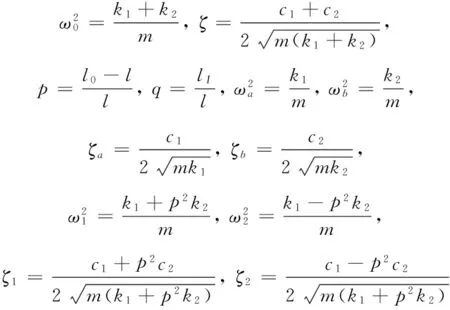
(4)

可得到矩陣形式的方程

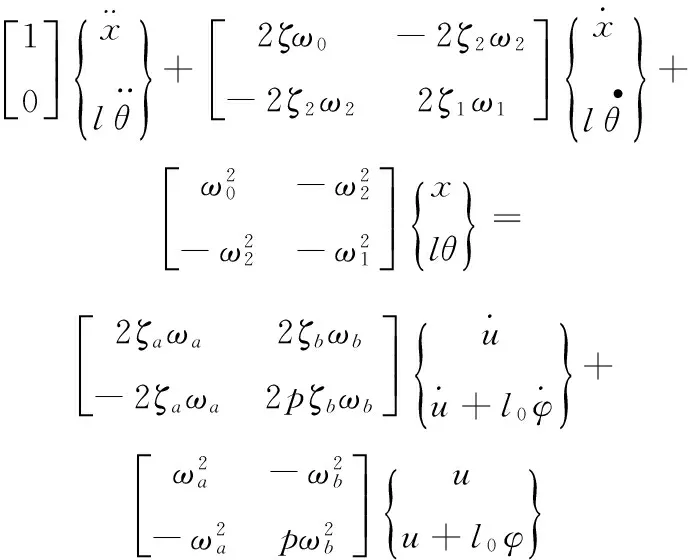
(5)

對式(5)進行分析，可得到慣組基座和慣組減振系統的一些主要設計原則：

1) 耦合振動的存在使設計異常復雜。為了避免出現線角耦合振動，使式(5)左邊斜對角項為0，通常取參數

k1=k2,c1=c2

(6)

式(6)說明慣組基座的構型和慣組減振方式布置應采用對稱形式，特別是空間的對稱形式，并且限制組合系統質心與彈性中心距離。在GJB 2503A—2004《慣性平臺減振器通用規范》中，要求安裝減振器后系統質心與彈性中心在一個以彈性中心為球心的直徑為φD的球內[22]。

2) 經過結構解耦后，圖3所示模型線振動、角振動剛度由式(7)和式(8)表示：

線剛度：

k=k1+k2

(7)

角剛度：

kφ=k1l2+k2(l0-l)2

(8)

單獨的線振動、角振動傳遞率均可轉化為式(9)所示的單自由度系統隔振傳遞率的標準形式。

(9)

不同頻率比和阻尼比下傳遞率如圖4所示。

因角振動傳遞特性直接關系姿控設計，為減少測量誤差，角振動頻帶盡可能寬。從式(8)可知，增大線振動剛度和減振器距離均可增加角剛度。但增加減振器剛度會影響線振動減振效率。從圖4可知，需要對峰值放大倍數Q和減振效率η統籌考慮，一般在滿足總減振效率的前提下，盡量采用較大剛度的減振器。阻尼的選取也不應太小。

3) 慣組基座彈性在很大程度上會影響慣組小系統減振效率。考慮到基座與慣組減振器的串聯設計，一般應盡量提高基座剛度，依靠慣組減振器減振。

實際更復雜的系統可采用六自由度模型，見文獻[7-9]和文獻[18]。慣組減振采用二自由度模型得出的結論與六自由度模型得出的結論類似，參見文獻[9]。

2 捷聯慣組基座的構型設計和典型構型模態特性分析

依據上節分析，慣組基座構型設計應滿足以下條件：

1) 盡量采用對稱結構布局，避免線、角運動耦合；

2) 應控制慣組小系統質心與慣組基座彈性中心距離，盡量將小系統質心設計在慣組基座安裝平面內，避免出現線、角耦合振動；

3) 盡量增加基座剛度，包括選用剛度較高的結構構型、采用剛度高密度小材料。

對慣組基座進行模態分析可對基座的動態特性做出評估。典型結構可以包括以下5種：

1) 構型1：“H型”布局；

2) 構型2：“H型-偏心”布局；

3) 構型3：“Y型”布局；

4) 構型4：“十字型”布局；

5) 構型5：“井字型”布局。

對上述5種構型進行有限元模態計算，慣組質量均為10 kg，慣組基座材料為鋁，截面為“工”字型，垂直方向高度100 mm，壁厚5 mm，基座長1 000 mm，計算結果參見圖6和表1。

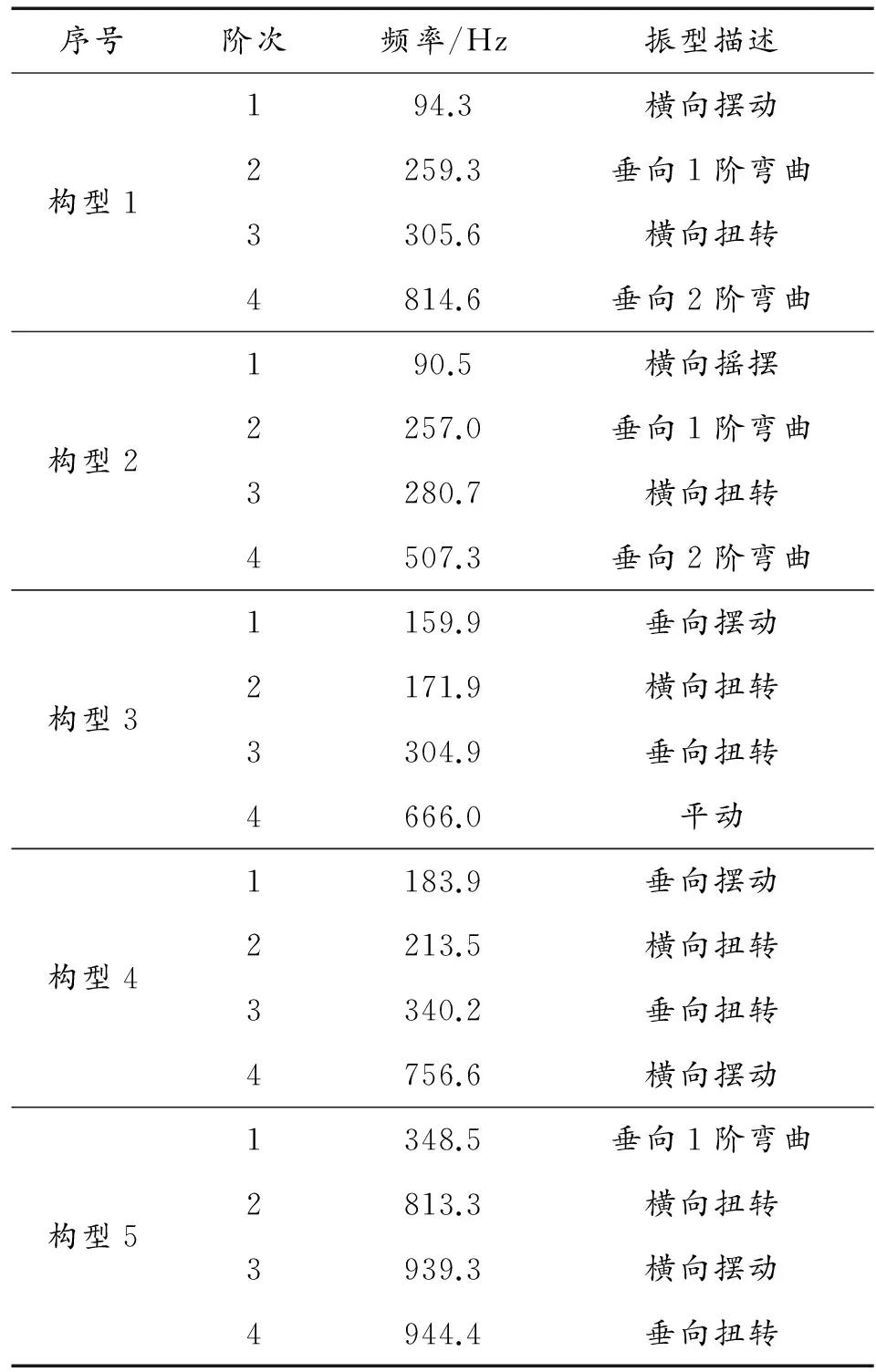
序號階次頻率/Hz振型描述構型1194.3橫向擺動2259.3垂向1階彎曲3305.6橫向扭轉4814.6垂向2階彎曲構型2190.5橫向搖擺2257.0垂向1階彎曲3280.7橫向扭轉4507.3垂向2階彎曲構型31159.9垂向擺動2171.9橫向扭轉3304.9垂向扭轉4666.0平動構型41183.9垂向擺動2213.5橫向扭轉3340.2垂向扭轉4756.6橫向擺動構型51348.5垂向1階彎曲2813.3橫向扭轉3939.3橫向擺動4944.4垂向扭轉

3 結論

從模態計算結果可知：

1) “H型-偏心”布局固有頻率最低，繞基座長軸方向剛度最差，存在較為嚴重的橫向擺頭運動，偏離了減小慣組小系統質心與慣組基座彈性中心距離的原則，在外界激勵下慣組小系統存在較為嚴重的線-角耦合振動。“H型”布局固有頻率比“H型-偏心”高，但繞長軸方向剛度低。

2) “Y型”、“十字型”、“井字型”布局具有較高的線振動和角振動固有頻率，并且第1階振型均為線振動，三種構型的角振動、線振動頻率比分別為1.07、1.16、2.33。“井字型”具有最高的線、角振動頻率。“十字型”是在“Y型”基礎上增加了一條安裝支腿，“井字型”是將“十字型”的每條支腿拓展為兩條支腿，增加了間距。

3) 五種構型中，“Y型”、“十字型”、“井字型”符合對稱結構布局要求，為相對較好的結構布局形式。

：

[1] DAVID H,TITTERTON,JOHN L,WESTON.捷聯慣性導航技術[M].北京：國防工業出版社，2007.

[2] 龍樂豪主編.液體彈道導彈與運載火箭系列：總體設計(中)[M].北京：宇航出版社，1989.

[3] 薛祖瑞.關于捷聯慣導系統圓錐誤差的詮釋[J].中國慣性技術學報，2000,8(4):46-50.

[4] 張丹，熊智，于永軍，等.捷聯慣導圓錐誤差補償算法[J].四川兵工學報，2011,32(1):100-103，123.

[5] 翟有新，馮培德.振動條件下平臺角振動對慣導系統誤差的影響研究[J].中國慣性技術學報，2000,8(1):1-6.

[6] 余楊，張洪.捷聯慣導系統中的圓錐運動和偽圓錐運動研究[J].中國慣性技術學報，2006,14(5):1-4.

[7] 姚建軍.結構參數對捷聯慣導系統靜態圓錐運動的影響[J].中國慣性技術學報，2008,16(3):294-300.

[8] 姚建軍，付繼波.捷聯慣導系統振動耦合特性研究[C]//首屆全國航空航天領域中的力學問題學術研討會論文集(下冊)，成都：中國力學學會，2004.294-298.

[9] 付繼波，馬靜，姚建軍.彈性支撐慣導系統振動耦合問題研究[J].強度與環境，2005,32(2):46-51.

[10]姚建軍.捷聯慣導系統不同隔振模式的比較[J].強度與環境，2009,36(2):19-27.

[11]謝燕，雷勇軍，周建平，等.慣導減振系統的結構參數的優化[J].強度與環境,2005,32(4):39-45.

[12]田亞軍，周剛，胡軍照，等.捷聯慣導系統姿態算法實現及工程應用[J].四川兵工學報，2011,32(1):10-12，23.

[13]李俊峰，劉進江，唐獻林.激光陀螺捷聯慣性組合的系統結構抗振控制[J].中國慣性技術學報，2006,14(1):21-26.

[14]王海峰，吳斌，張敏，等.激光捷聯慣導減振系統設計與應用[J].航天控制，2007,25(6):91-89.

[15]楊富鋒，芮筱亭，馬蕾.激光陀螺捷聯慣導減振系統動力學建模與仿真[J].中國慣性技術學報，2008,16(3):301-305.

[16]楊朋軍，孟進錄，張天孝.捷聯慣性測量組合臺體組件設計與分析[J].宇航學報，2010,31(1):162-166.

[17]張志鑫，張大偉.捷聯慣組減振系統角振動、線振動共振頻率理論分析[J].中國慣性技術學報，2009,17(6):654-657.

[18]吳斌，王海峰，曲濤，等.彈載激光陀螺慣導系統安裝支架設計[J].中國慣性技術學報，2007,15(2):132-135.

[19]謝燕.慣導支架結構的隨機動力響應分析與參數優化[D].長沙：國防科學技術大學，2004.

[20]丁文鏡.減振理論[M].北京：清華大學出版社，1988.

[21]NOLL R B，ZVARA J.Structural Interaction with Control Systems [R].NASA SP-8079,1971.

[22]GJB 2503A—2004，慣性平臺減振器通用規范[S].