新型遠程制導炸彈攻擊區影響因素研究

龐 威，謝曉方，鄭力會,孫 濤，孫海文,孫明軍

(1.海軍航空工程學院， 山東 煙臺 264001； 2.海軍駐洛陽地區航空設備軍事代表室， 河南 洛陽 471009)

新型遠程制導炸彈是在傳統炸彈上加裝滑翔彈翼、紅外圖像導引頭和控制系統，以提高升阻比增大射程自主攻擊目標。準確地求解出制導炸彈的攻擊區對新型制導炸彈的設計改造和使用具有指導意義。

新型制導炸彈在載機投放后展開滑翔彈翼飛行，當滑翔到目標附近時紅外圖像導引頭開機(即導引頭啟控點)搜索目標，當捕獲到目標時，采用設定的導引律自主攻擊目標，其攻擊過程如圖1所示。顯然，為實現遠距離防區外投放，應當關注制導炸彈攻擊區的遠界。炸彈能否打擊到目標可根據當前狀態下的攻擊區判斷，當目標位于攻擊區之內時，即可按照給定的要求成功攻擊目標；當位于攻擊區之外，則攻擊目標失敗。其攻擊區主要受紅外圖像導引頭捕獲到目標時，炸彈當前姿態(如彈道傾角，速度等)和側風等的影響。文獻[1]通過建立激光制導炸彈的六自由運動方程，仿真了水平投彈時激光制導炸彈的投放區域，但并未對影響因素進行分析；文獻[2]將傳統機械射表與模型解算相結合，采用局部精確搜索，提出了一種新型空地制導炸彈可攻擊區的求解方法；但主要針對已經生產和列裝的制導炸彈，對于還在設計、論證和改造中的制導炸彈，由于其還在論證過程中，不能采用此法。文獻[3]針對機載火控計算機實時攻擊區的計算和精度等要求，采用回歸模型分段擬合制導炸彈的攻擊區；文獻[4-6]中針對空空導彈攻擊區的實時求解問題，提出了一種變步長積分和黃金分割的求解方法。文獻[7]利用傾側角反轉和粒子群算法相結合的方法研究了升力式高超聲速飛行器的可達域。文獻[8]利用Gauss偽譜法研究了制導炸彈的最優彈道求解，但并未研究可攻擊區。文獻[9]以高超聲速飛行器中的攻角作為狀態變量，側滑角作為控制變量，采用Gauss偽譜法研究了高超聲速的可達域。文獻[10-11]研究了制導彈藥中制導律和攻擊軌跡的設計。

綜上所述，現有的研究主要集中在制導律的設計[12-15]和攻擊區[16-19]的求解，對影響制導炸彈攻擊區的相關因素研究較少。本研究以制導炸彈的攻角和側滑角為控制變量，采用比例導引法研究了影響攻擊區的相關因素，并進行了仿真分析。

1 數學建模

1.1 空氣動力模型

由于側風對制導炸彈的飛行彈道具有一定的影響，因此需要研究側風對攻擊區的影響，建立風速矢量在地面水平坐標系下的表達式為

(1)

在實際運用中，通常只考慮風的來向角，不考慮垂直風的影響[20]，因此

(2)

式中：vw=|vw|，表示風速矢量的大小；ψw表示風的來向方位角，以發射坐標系中繞炸彈高度逆時針旋轉方向為正。

由此可得制導炸彈速度相對于風速的相對速度

(3)

(4)

因此，制導炸彈在飛行過程中所受的氣動力為

(5)

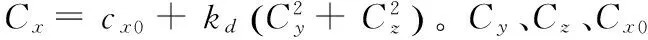
1.2 制導炸彈的動力學方程

根據前文分析，制導炸彈的攻擊區主要取決于導引頭啟控點處炸彈的各種參數，由于此時炸彈飛行高度較低，且飛行距離相對較短，本文做以下假設：

1) 將炸彈視為質點，整個過程中炸彈質量不變，不考慮形變等因素；

2) 不考慮地球曲率和轉動的影響，將地面視為水平面；

3) 將炸彈的控制系統視為無延時的控制系統。

根據以上假設，在地面水平坐標系下建立制導炸彈的動力學方程

(6)

式中，xm,ym,zm分別表示制導炸彈的縱向射程、高度和側向射程；vm,θm,ψm分別表示制導炸彈的速度、攻角和彈道偏角；nα,nβ分別表示法向過載和側向過載；根據文獻[21]對過載的定義，可求解出制導炸彈所受過載的表達式，即

(7)

1.3 制導律模型

新型制導炸彈是加裝紅外圖像末制導導引頭的無旋制導炸彈，滾轉角速度和滾轉角較小[22]，為研究方便，本研究忽略其影響，因此制導炸彈的導引律可分解為俯仰和偏航兩個平面上的導引律[23]，視線角速度為

(8)

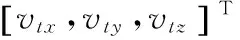
(9)

式中：Nα和Nβ為比例系數。

2 攻擊區的求解

攻擊區是指由炸彈攻擊最遠目標的遠距離包絡線和攻擊最近目標的近距離包絡線圍成的區域，可首先采用黃金分割方法求解出二維縱向平面內的最大和最小射程，然后以此結果為初始值，代入到彈道方程中，再采用黃金分割算法求解側向平面的最大射程。采用黃金分割方法的基本原理為，首先給定縱向初始射程的最大范圍[x0,xf]；計算出黃金分割點的坐標：xR=x0+0.618(xf-x0)，然后以分割點的位置作為縱向射程的虛擬目標，采用比例導引法求解彈道，之后判斷求解結果能否滿足設定約束(指脫靶量過大或攻角、側滑角等是否滿足約束條件)；若不能滿足條件，則需要更新射程范圍區間，令xf=xR，繼續求解黃金分割點；若滿足條件，令x0=xR；直到求解出的縱向射程區間長度滿足設定的求解誤差為止，即|x0-xf|≤ε。對于最小射程，采用相同的方法求解即可。以最大縱向射程xmax為起始值，以d設定步長，采用黃金分割方法求解坐標位于(xmax-nd,0)對應的側向射程(其中n為整數)，直到xmin時求解結束。其詳細求解流程如圖2所示。

3 仿真分析

3.1 無干擾情況下的攻擊區

以文獻[24]的新型滑翔增程制導炸彈為例，載機投放后炸彈展開滑翔彈翼飛向預先載入的目標點，當到達目標上空附近時，導引頭開機搜索目標(即導引頭啟控點)，設此時炸彈的位置為(2 000 m,0 m,0 m)；速度為vm(t0)=300 m/s，彈道傾角θ(t0)=0°；彈道偏角為ψ(t0)=0°；炸彈的質量m=557.1 kg，參考面積為Sref=0.116 m2,重力加速度取g=9.81 m/s2，即：

制導炸彈啟控點的狀態

(10)

在攻擊目標的過程中，為了保證控制變量約束的要求，設定過程約束為

(11)

終端約束為

y(tf)=0 m

(12)

設定求解誤差ε≤5 m；比例導引律的系數Nα=3和Nβ=4；步長d=10 m;仿真的彈道如圖3所示。

圖3展示了制導炸彈的彈道仿真結果，求解虛擬目標點的坐標為(14 700 m,4 300 m)。從圖3(c)中可以看出采用比例導引方法求解的制導炸彈的彈道軌跡滿足攻角和側滑角的約束。

圖4展示了制導炸彈的攻擊區，其中設定的誤差為ε≤5 m。圖4(a)中方塊表示虛擬目標的點。由3種線條圍成的包絡為制導炸彈的攻擊區。圖4(b)表示制導炸彈攻擊區在地平面的結果。從圖4可以看出，制導炸彈攻擊區近界側向攻擊區邊界較小，這是由于炸彈采用無動力滑翔飛行，縱向射程較小，飛行時間短，且側向力系數也較小，從而導致側向射程較小。

3.2 側風對攻擊區的影響

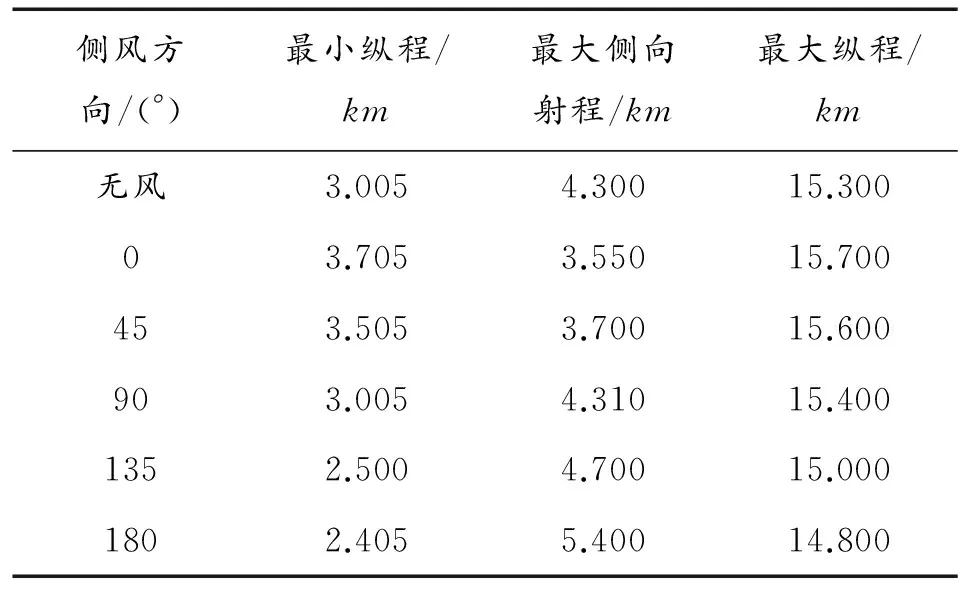
以3.1節中各種初始條件和過程、終端約束為例，研究側風對攻擊的影響。仿真中設置側風大小為30 m/s，炸彈在啟控點處的速度vm(t0)=300 m/s，研究風的來向角分別為ψw=0°，ψw=45°，ψw=90°，ψw=135°，ψw=180°時制導炸彈的攻擊區，仿真結果如圖5和表1所示。

側風方向/(°)最小縱程/km最大側向射程/km最大縱程/km無風3.0054.30015.30003.7053.55015.700453.5053.70015.600903.0054.31015.4001352.5004.70015.0001802.4055.40014.800

從圖5和表1可以看出側風對攻擊區縱向邊界影響相對較小，但對于側向攻擊區影響較大。例如側風風向為零度時，此時可認為制導炸彈在縱向飛行方向“順風”，根據式(4)和式(5)可得相對風速變小，其對應的攻角和側滑角相對于無側風時變小，因此當滿足最大攻角約束時，縱向射程會相應增大。觀察圖5和表1，側風并未使攻擊區產生較大的偏移，分析原因主要是兩個：① 側風相對于炸彈速度較小，由此導致的相對速度變化不大，從而側向力較小，側向射程偏移偏小。② 制導炸彈的側向力系數相對于升力系數和阻力系數較小，由此產生的側向力小，從而側向力小，側向射程偏移較小。仿真過程中發現考慮側風因素時，攻擊區相對無風的偏移僅為0～200 m；偏移量較小。因此在實際運用過程中可忽略側風的影響。

3.3 初始速度對攻擊區的影響

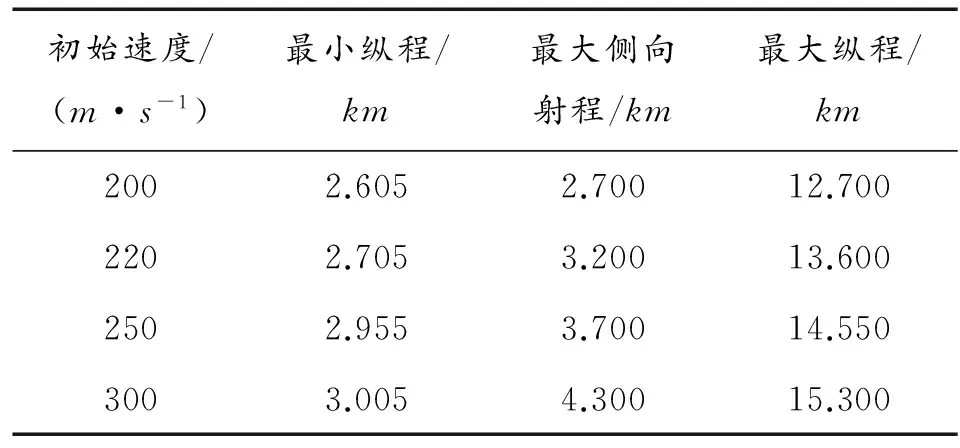
以3.1節中各種初始條件和過程、終端約束為例，研究導引頭啟控點處炸彈速度對攻擊區的影響。仿真中分別設置炸彈在導引頭啟控點處的速度分別為vm(t0)=300 m/s，vm(t0)=250 m/s,vm(t0)=220 m/s，vm(t0)=220 m/s時，求解制導炸彈的攻擊區，仿真結果如圖6和表2所示。

從圖6和表2可以看出，導引頭啟控點處炸彈的速度對攻擊區的縱向和側向最遠邊界影響較大。速度從200 m/s增加到250 m/s時，攻擊區最大縱向射程從12.7 km增加到14.55 km，增加幅度達1.85 km；而從250 m/s增加到300 m/s時，縱向射程增幅僅為0.75 km。圖5所示攻擊區隨著啟控點處炸彈速度的增加而增大，這是由于制導炸彈采用無動力滑翔，在滑翔過程中動能和重力勢能克服阻力做功，同時增加下滑速度，增大動能；初始動能的增大從而導致可攻擊區的增加；制導炸彈的極限射程與初始速度正相關且初始速度對攻擊區的影響較大，在進行制導炸彈的設計和運用中，可根據攻擊目標的實際情況，調整制導炸彈導引頭啟控點處的速度來滿足區域覆蓋的打擊要求。

初始速度/(m·s-1)最小縱程/km最大側向射程/km最大縱程/km2002.6052.70012.7002202.7053.20013.6002502.9553.70014.5503003.0054.30015.300

3.4 初始彈道傾角對攻擊區的影響

以3.1節中各種初始條件和過程、終端約束為例，研究導引頭啟控點處炸彈彈道傾角對攻擊區的影響。仿真中分別設置啟控點處炸彈的彈道傾角為θ(t0)=-10°，θ(t0)=0°，θ(t0)=10°，速度為vm(t0)=250 m/s時，求解制導炸彈的攻擊區，仿真結果如圖7和表3所示。

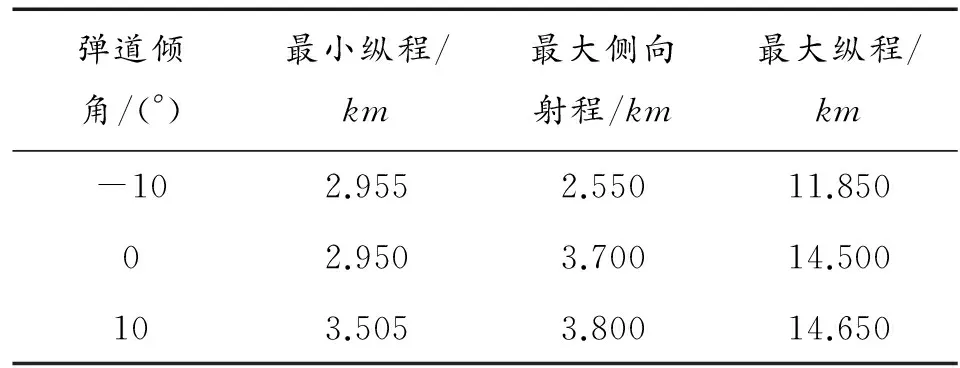
彈道傾角/(°)最小縱程/km最大側向射程/km最大縱程/km-102.9552.55011.85002.9503.70014.500103.5053.80014.650

從圖7可以看出制導炸彈的攻擊區關于縱向射程對稱。表3中，初始彈道傾角從-10°增加到0°時，攻擊區最大側向射程從2.55 km到3.7 km，增量達1.15 km，增幅達45.1%；縱向最大射程從11.85 km增加到14.50 km，增量為2.65 km，增幅為22.36%；而彈道傾角從0°增加到10°時，攻擊區最大側向射程從3.7 km到3.8 km，增量為0.1 km，增幅為2.7%。縱向最大射程從14.50 km增加到14.65 km，增量為0.15 km，增幅僅為1.03%。從表2和圖6中可以看出，制導炸彈的攻擊區隨著導引頭啟控點處彈道傾角的增大而增大，當彈道傾角小于零時，增大彈道傾角對攻擊區的影響較大；彈道傾角大于零時，增大彈道傾角對攻擊區的影響相對較小。因此，在實際運用過程中，為增大攻擊區域，應調整彈道傾角，使其大于零，以便達到更好的攻擊效果。

3.5 導引頭啟控點高度對攻擊區的影響研究

以3.1節中各種初始條件和過程、終端約束為例，研究導引頭啟控點處炸彈的高度對攻擊區的影響。仿真中分別設置在導引頭啟控點處炸彈的高度為：ym(t0)=1 500 m，ym(t0)=2 000 m,ym(t0)=2 500 m，速度vm(t0)=250 m/s時，求解制導炸彈的攻擊區，仿真結果如圖8和表4所示。

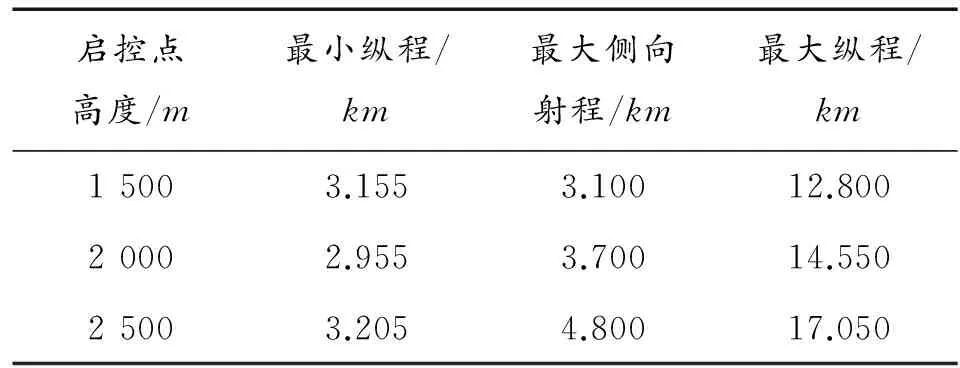
啟控點高度/m最小縱程/km最大側向射程/km最大縱程/km15003.1553.10012.80020002.9553.70014.55025003.2054.80017.050

從圖8可以看出制導炸彈的攻擊區關于縱向射程對稱。當高度從1 500 m增加到2 000 m時，最大縱程總12.8 km增加到14.55 km，增幅為13.7%；從2 000 m增加到2 500 m時，最大縱程增量為2.5 km，增幅為17.5%；顯然，炸彈高度從2 000 m到2 500 m的最大縱向攻擊區增幅大于1 500 m到2 000 m，產生這種現象的原因為：由于高度越高，大氣密度越小，阻力越小；在同樣初始動能情況下，根據物理學定律，炸彈所處位置越高，其重力勢能越大，而在高度較高的地方由于空氣密度較低，需要克服的阻力較小，從而導致縱向射程增加量大于較低高度的增量。因此，在實際運用過程中，可根據導引頭的探測距離設定導引頭啟控點的高度來增大攻擊區域，以便達到更好的攻擊效果。

4 結論

以某新型紅外圖像制導炸彈為研究對象，采用比例導引律研究了影響制導炸彈攻擊區的各種因素，通過計算和數值仿真表明：

1) 采用黃金分割法能夠較為精確的求解出制導炸彈的攻擊區，可用于不同啟控點條件下制導炸彈彈道和攻擊區的求解。

2) 制導炸彈導引頭啟控點處的速度和高度與攻擊區的范圍成正相關，在相同終端約束條件下，啟控點處的速度越大，攻擊區的范圍就越大；高度越高，攻擊區的相對增量也越大。

3) 制導炸彈導引頭啟控點處的彈道傾角對攻擊區的影響較大，并且當彈道傾角小于零且逐漸減小時，可攻擊區域縮小較快；在彈道設計和運用工程中，為增大攻擊區應當使導引頭啟控點炸彈處于平飛或抬頭飛行狀態。

需要指出的時，本文主要分析了影響制導炸彈攻擊區遠界的部分因素，考慮氣動模型誤差和大氣密度變化對攻擊區的影響是下一步研究的方向。

：

[1] 謝奇峰,馮金富,于雷,等.激光制導炸彈投放域分析[J].火力與指揮控制,2006,31(5):57-60.

[2] 李強,夏群利,崔瑩瑩,等.空地制導炸彈可攻擊區的快速解算方法[J].兵工學報,2012,33(4):390-394.

[3] 雷科,林忠賢.制導炸彈攻擊區擬合算法研究[J].電光與控制,2013,20(2):85-88.

[4] 周燦輝,周德云,聶志強,等.中程空空導彈可攻擊區解算的新方法[J].火力與指揮控制,2012,37(7):54-56.

[5] 張平,方洋旺,喬治軍,等.超視距空空導彈協同允許發射區解算方法[J].電光與控制,2012,19(3):12-16.

[6] 丁達理,王鈾,黃濤,等.一種空地導彈攻擊區快速解算方法[J].空軍工程大學學報:自然科學版,2014,15(6):6-10.

[7] 趙江,周銳.基于粒子群優化的再入可達區計算方法研究[J].兵工學報,2015,36(9):1680-1687.

[8] 龐威,謝曉方,孫濤,等.基于Gauss偽譜法的制導炸彈最優彈道研究[J].南京理工大學學報,2017,41(1):12-21.

[9] 王濤,張洪波,李永遠,等.Gauss偽譜法的再入可達域計算方法[J].國防科技大學學報,2016,38(3):75-80.

[10]DOHRMANN C R,EISLER G R,ROBINETT R D.Dynamic programming approach for burnout-to-apogee guidance of precision munitions[J].Journal of Guidance,Control,and Dynamics,1996,2(19):340-346.

[11]HUI Y,NAN Y,CHEN S,et al.Dynamic attack zone of air-to-air missile after being launched in random wind field[J].Chinese Journal of Aeronautics,2015,28(5):1519-1528.

[12]李偉明,孫瑞勝,白宏陽,等.變后掠翼航彈最優彈道自適應滑模跟蹤控制[J].系統工程與電子技術,2015,37(2):372-378.

[13]白宏陽,李偉明,孫瑞勝,等.航空時敏制導炸彈增程彈道組合優化設計[J].國防科技大學學報,2014,36(6):100-105.

[14]RATNOO A,GHOSE D.Impact angle constrained interception of stationary targets[J].Journal of Guidance,Control and Dynamics,2008,31(6):1816-1821.

[15]RUSNAK I,WEISS H,ELIAV R,et al.Missile guidance with constrained intercept body angle[J].IEEE Transactions on Aerospace and Electronic Systems,2014,50(2):1145-1453.

[16]黃國強,南英,陳芳,等.風場中無動力滑翔彈可攻擊區研究[J].飛行力學,2008,26(4):47-50.

[17]汪雷，劉欣，楊濤,等.高超聲速滑翔式飛行器目標覆蓋范圍的計算方法[J].彈道學報,2014,26(1):50-55.

[18]梁卓,管雪元,孫瑞勝,等.基于復合制導律的“慣性/衛星”制導炸彈投放域計算[J].彈道學報,2007,19(3):27-30.

[19]李波,高曉光.基于機會約束規劃的空空導彈期望值廣義攻擊區[J].彈道學報,2013,25(3):13-17.

[20]黃國強,南英,陳芳,等.考慮各種隨機干擾源有控炸彈攻擊區及彈道仿真研究[J].彈箭與制導學報,2009,29(5):193-196.

[21]孟克子，周荻.過載指令約束下的導彈導引律設計[J].兵工學報,2014,35(9):1419-1427.

[22]陳琦，王中原，常思江，等.不確定飛行環境下的滑翔制導炮彈方案彈道優化[J].航空學報,2014,35(9):2593-2604.

[23]張煜，王楠，陳璟，等.空地多目標攻擊中制導炸彈可投放區計算研究[J].兵工學報,2011,32(12):1474-1480.

[24]袁宴波,張科,薛曉東.基于Radau偽譜法的制導炸彈最優滑翔彈道研究[J].兵工學報,2014,35(8):1179-1186.