多假目標干擾下組網雷達機動目標跟蹤方法

包守亮，程水英，許登榮

(國防科技大學電子對抗學院，安徽 合肥 230037)

0 引言

隨著現代電子戰的迅速發展，電子對抗愈加激烈，防空作戰體系面臨的環境日益復雜，對雷達的作戰效能提出了更高要求[1-2]。動目標檢測(Moving Target Detection, MTD)技術的應用，使得無源干擾很容易被識別并剔除[3]。因此，現代雷達的主要威脅來源于有源干擾，尤其是先進數字射頻存儲器(Digital Radio Frequency Memory, DRFM)的發展，可以瞬間截獲、存儲和轉發雷達信號，形成時域、頻域，甚至空域特征都十分逼真的虛假信號，先進的信號處理系統難以完全消除干擾對雷達的影響，虛假信號不可避免會進入數據處理器，不僅降低對目標跟蹤的精度，也嚴重消耗雷達資源[4]。因此，如何有效對抗這種逼真度很高的虛假信號，對于提升雷達作戰效能具有重要意義。

針對距離欺騙式干擾，國內外學者進行了大量研究[5-9]。文獻[5]采用加權概率數據互聯算法(Probabilistic Data Association Filter, PDAF)消除距離欺騙干擾的影響；文獻[6]在紐曼皮爾遜準則下構建兩種二元假設檢驗識別距離假目標；文獻[7—8]利用量測角度同源及信號似然比檢驗識別干擾是否存在；而文獻[9]則針對多假目標干擾利用量測角度統計特性差異識別真假目標。以上文獻都是基于單部雷達的抗干擾算法。由于單部雷達視角單一，獲取信息量少，對抗效果不佳，文獻[10]開創性地研究了組網雷達抗干擾技術。隨后，該技術得以廣泛應用。其中，文獻[11]研究了多假目標干擾下雷達網的優化選擇問題；文獻[12]是組網雷達抗多假目標干擾的代表性文獻，通過量測的預處理，問題轉化為單雷達的多目標跟蹤；文獻[13—14]則對多假目標干擾下目標的低可觀測性展開了研究。然而上述文獻大多針對非機動目標設計抗干擾算法。現代戰爭中，為提高干擾效能，目標往往在機動時釋放干擾，導致目標跟蹤精度及抗干擾性能急劇下降。針對上述算法的不足，本文基于組網雷達提出了多假目標干擾下的機動目標跟蹤方法。

1 多假目標干擾下目標量測模型

為方便論述，以兩部雷達組網為例(對3部及以上的雷達組網，方法同樣適用)。如圖1所示，假設兩部雷達觀測同一片空域，且同步采樣。各雷達的坐標為(xi,yi,zi)，i=1,2代表第i部節點雷達。

假設空間中存在一個真實目標，每個時刻自衛式干擾機產生n個虛假目標。根據虛假目標與真實目標角度同源，其俯仰角與方位角近似相等，而與真實目標的徑向距離差值為Δρj，其中j=1,2,…,n。Δρj為正，代表比真實目標遠，Δρj為負，代表比真實目標近。空域中除真實目標與虛假目標外，還分布有一定數量的雜波和虛警。

雷達在跟蹤目標時，從回波信號中提取的有用信息除了目標到雷達的距離、方位，通常還包含信號強度，即回波信號的功率，歸一化噪聲背景下，等于回波信噪比。對于Swerling1起伏模型，信噪比的概率密度函數為[15]：

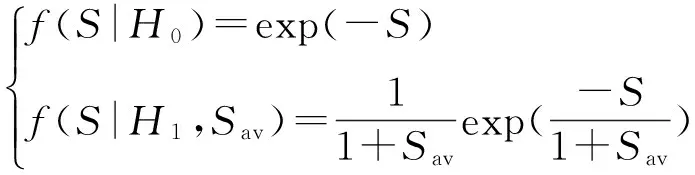
(1)

式中，“H1假設”和“H0假設”分別代表回波中存在和不存在目標信號，S為實際信噪比，Sav為期望(平均)信噪比。

設雷達的歸一化檢測門限為Th，確認量測是指功率超過檢測門限的量測，因此其信噪比的概率密度函數可表示為[15]：

(2)

式中，PD、PFA為雷達的檢測概率和虛警概率，且

PD=1/(1+Sav)exp{-Th/(1+Sav)}

(3)

PFA=exp(-Th)

(4)

假設由式(2)計算得到的雜波和真實目標信噪比分別為Sn、ST。則依據虛假目標功率通常為真實目標功率的γ倍[16]，有：

SF=γST

(5)

式中，γ～U(a,b)，即在區間(a,b)上服從均勻分布。至此，可建立雜波、真實目標、虛假目標的信/干噪比模型。

(6)

(7)

(8)

(9)

式中，ΔR為距離分辨率，σφF、σθF為量測角度隨機偏差，σφB、σθB為角度系統偏差，σφN、σθN由下式進行計算：

(10)

(11)

其中，A為方位波束寬度，E為俯仰波束寬度。

(12)

2 多假目標干擾下機動目標跟蹤方法

2.1 量測的劃分與融合

雷達觀測的空域中，除真實目標與虛假目標，還分布有一定數量的雜波，若直接采用卡方檢驗進行量測劃分，容易將雜波-雜波、雜波-目標量測對誤判為目標-干擾量測對并入量測集，影響融合精度。因此，卡方檢驗前首先進行信號似然比預處理可以提高量測劃分的準確性。

2.1.1信號似然比預處理

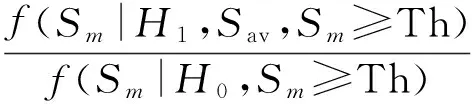
(13)

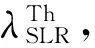
2.1.2角度卡方檢驗

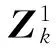
(14)

易知，Tlj是服從自由度為2的χ2分布，通過單邊假設檢驗可判斷兩個量測是否角度同源：

(15)

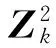
2.2 構建濾波輸入量測

從2.1節可知，每部雷達通過量測的劃分與融合，可以確定一條直線。理想情況下，兩部雷達所得的直線應交于一點，該點即為真實目標位置。由于存在量測誤差，空間中這兩條直線相交的概率很小，但是，一般也不會離得“太遠”，即有很大的概率落在距真實目標量測較小的距離范圍內。對這兩條直線求最小二乘解，可以得到“廣義”的交點，即“中心量測”，如圖2所示。易知，“中心量測”離真實目標一定不遠[13]。

依據該特點，文獻[13]直接利用“中心量測”進行濾波更新。根據最小二乘的定義，兩條異面直線的最小二乘解在公垂線的中點。因此，如果兩部雷達的真實目標量測不在垂足點，那么“中心量測”并不是最優的輸入量測。鑒于該量測離真實目標量測比較近，因此利用該量測進行最近距離關聯，則有很大概率得到各雷達真實的目標量測，再進行數據融合，可以得到精度更高的輸入量測。

2.2.1求解“中心量測”

(16)

其中，i=1,2代表兩部節點雷達。據此建立如下的方程組[13]：

A(x,y,z)T=b

(17)

其中：

(18)

(19)

對式(18)求解，可得“中心量測”為：

(20)

2.2.2濾波輸入量測的構建

假設將中心量測Zc轉換到球坐標系得到量測zc=[ρc,θc,φc]T，則計算zc與各雷達關聯量測集中每個量測的徑向距離差：

(21)

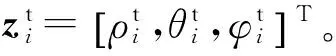
(22)

(23)

(24)

2.3 機動目標跟蹤

對于機動目標跟蹤，IMM算法通過合理的假設管理，一般被認為是混合系統中最有效的估計方式，并得到了廣泛應用。根據多假目標干擾的存在與否，分兩種情況進行濾波更新。

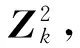
2)如果不滿足第1)類情況，則認為多假目標干擾不存在，各節點雷達采用基于幅度特征的IMMPDAF算法(IMM-PDAFAI)進行濾波更新，然后利用式(23)～式(25)進行數據融合。與標準的IMMPDAF算法相比，IMM-PDAFAI算法在計算互聯概率時加入了信號似然比，其互聯概率的計算公式為[18]：

(25)

(26)

其中，λm為第m個量測的信號似然比，由式(13)給出。其他參數說明詳見文獻[18]。

3 仿真結果與分析

3.1 量測關聯結果與分析

輸入量測的構建依賴于各雷達量測的準確劃分與關聯，因此，首先對第2節量測劃分與關聯的準確性進行驗證。假設干擾機每個時刻產生6個虛假目標，在真實目標前后均勻分布，間隔為1 km，功率為真實目標的γ倍，γ～U(2,4)。各節點雷達的采樣間隔均為T=1 s，虛警概率PFA=0.001，跟蹤門概率PG=0.997，跟蹤門限γ0=16，雜波在觀測區域內均勻分布，密度為2×10-10個/m3。雷達其余參數設置如表1。

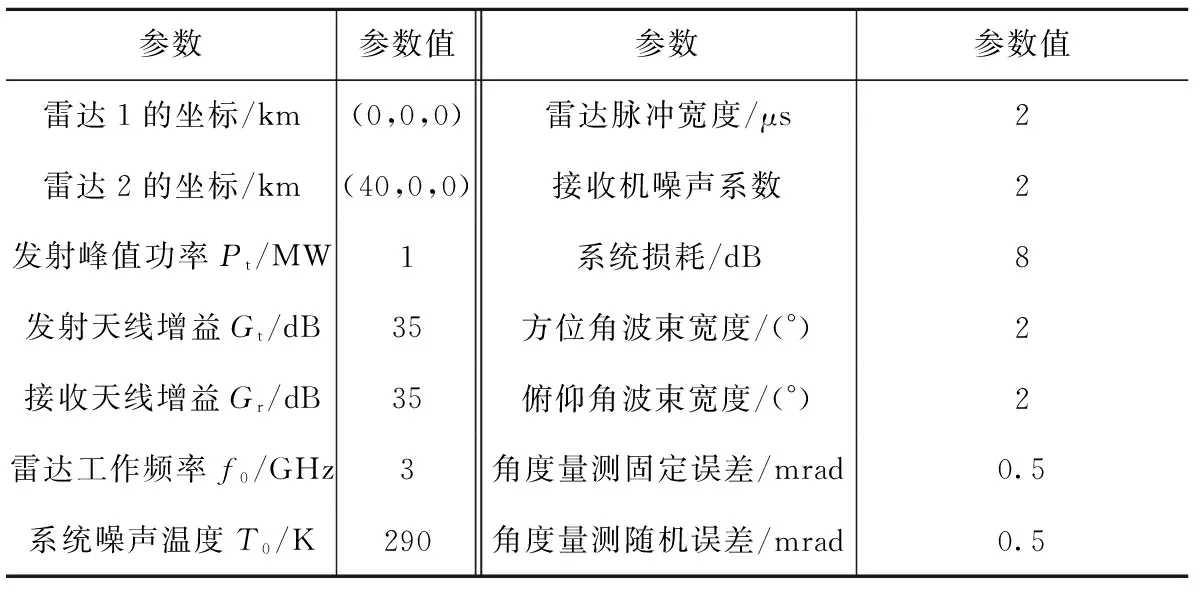
表1 雷達參數

在多假目標干擾存在時，量測集的正確劃分概率和量測正確關聯概率與目標位置有關，因此考慮讓目標位置在一定的區域內連續變化，變化范圍：

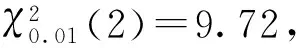
由圖4可知，通過似然比預處理，χ2檢驗對量測的正確劃分概率大部分區域趨近于1。距離雷達比較遠時，由于檢測概率下降比較快(如圖3)，量測的正確劃分概率有一定的降低。

圖5反映的是采用最近距離關聯手段正確選擇目標量測的概率，在距離雷達相對較近的區域，其準確關聯的概率也趨近于1。當距離雷達較遠時，由于量測噪聲的增加，正確關聯概率有一定的下降。此外，在y軸為0時，由于目標和兩部雷達位于同一直線上，方位誤差帶來的影響比較大，正確關聯概率相對較低。但實際情況下，目標不可能總是位于這一個平面內，因此，并不影響算法的實用性。

通過上述分析，預先對確認量測進行信號似然比處理，再進行χ2檢驗，各節點雷達可以有效進行量測劃分。同時，利用中心量測，也能準確關聯各節點雷達的真實目標量測，為后續的機動目標跟蹤奠定了基礎。

3.2 目標跟蹤結果與性能分析

選擇文獻[16]中典型的戰斗機機動場景(目標6)作為跟蹤對象，目標飛行188 s，初始高度為1 550 m，除83～114 s勻速下降外，其余時間都在等高平面運動，真實目標量測與虛假目標量測的分布情況如圖6所示。

本文采用通用的勻速(Constant Velocity, CV)模型、勻加速(Constant Acceleration, CA)模型和轉彎加速度未知的協同轉彎(Coordinate Turn, CT)模型構成的模型集來實現對目標狀態的混合估計。IMM，IMMPDAF，IMM-PDAFAI算法的Markov概率轉移矩陣以及初始模型概率均為：

(27)

進行200次Monte-Carlo仿真實驗，與文獻[13]中的方法進行比較。為體現本文輸入量測的有效性，文獻[13]與本文算法在數據預處理和跟蹤算法上完全相同，只在量測的選擇上有差異。同時，為驗證對虛假目標角度信息的充分利用以及組網雷達信息融合的優勢，將雷達1、雷達2在無多假目標干擾下采用IMMPDAF算法進行跟蹤的誤差曲線一并給出。圖7為各算法的位置和速度均方根誤差曲線，同時，對觀測時間內的平均均方根誤差及峰值誤差(15 s以后)進行了統計。

根據表2的統計結果，在多假目標干擾存在時，本文及文獻算法通過充分利用虛假目標提供的角度信息，以及融合多部雷達的觀測信息，可以大大減小量測噪聲帶來的隨機誤差，跟蹤精度較單部雷達有較大的提升，且目標機動時，對目標狀態的估計更加準確，誤差曲線更加平滑。雷達2比雷達1的跟蹤精度高主要是目標距離雷達2比較近，方位誤差明顯減小。

由圖7可知，相比文獻[13]，本文算法在量測選擇上占有較大優勢。通過中心量測進行最近距離關聯，準確選擇真實目標量測進行融合，更新濾波器，使得平均位置均方根誤差下降了57%，平均速度均方根誤差下降了14%，峰值誤差也得到了一定的改善。

在處理器Intel(R) Core(TM) i3-2350 CPU @ 2.3 GHz, RAM為4 GB的計算機上利用MATLAB 2014做200次Monte-Carlo仿真實驗，統計文獻[13]和本文算法單步仿真平均用時分別為0.0186 s、0.0191 s。可見，本文算法在構建輸入量測時，由于采用一維徑向最近距離關聯，增加的計算量很小，并不影響算法的實時性。

4 結論

本文提出了基于組網雷達的機動目標跟蹤方法。該方法通過信號似然比預處理與角度χ2檢驗相結合對各雷達進行量測分組，根據真假目標量測的空間分布特征求解中心量測，并基于該量測進行球坐標系下的徑向最近距離關聯，從而構造更高精度的濾波輸入量測。最后結合PDAFAI算法，在IMM算法的框架下實現對機動目標的高精度跟蹤。仿真結果表明，預先進行信號似然比預處理，結合角度χ2檢驗可以準確對量測進行分組，利用最近距離關聯所構建的輸入量測進行目標跟蹤可以取得更高的濾波精度(相比類似方法，其平均位置、速度均方根誤差分別減小了57%和14%)，且通過數據融合能進一步提升IMM算法對機動目標的跟蹤能力。

[1]張林讓，趙珊珊，周宇，等.網絡化雷達協同抗欺騙式干擾技術研究進展[J].數據采集與處理，2014，29(4)：516-525.

[2]沙文浩，姜秋喜，潘繼飛，等.網絡雷達對抗系統反隱身有源檢測模型[J].探測與控制學報，2017，39(5)：102-108.

[3]MAHAFZA.雷達系統設計MATLAB仿真[M].北京：電子工業出版社，2009.

[4]李迎春，王國宏，關成斌，等.速度拖引干擾和雜波背景下脈沖多普勒雷達目標跟蹤算法[J].電子與信息學報，2015(4)：989-994.

[5]KIRUBARAJAN T, BAR-SHALOM Y, BLAIR W D, et al. IMMPDAF for radar management and tracking benchmark with ECM[J]. IEEE Transactions on Aerospace & Electronic System, 1998, 34(4): 1115-1134.

[6]HOU J, LI X R, JILKOV V P, et al. Sequential detection of RGPO in target tracking by decomposition and fusion approach[C]//International Conference on Information Fusion. Singapore: IEEE, 2012: 1 180-1800 .

[7]周文輝，李琳，陳國海.一種有效的RGPO干擾鑒別算法及性能分析[J].電子學報，2007，35(6)：1165-1169.

[8]徐海全，王國宏，關成斌.RGPO干擾條件下一種改進的機動目標跟蹤方法[J].彈箭與制導學報，2010，30(4)：157-162.

[9]孫殿星，王國宏，李迎春，等.距離多假目標干擾下低可觀測目標跟蹤處理[J].電子學報，2016，44(4)：826-837.

[10]STAVROULAKIS P, FARSARIS N, XENOS T D. Anti-Jamming transmitter Independent radar networks[C]//International Conference on Signal Processing, Com. Cherbourg, France: IAPR, 2008: 269-273.

[11]楊忠，王國宏，孫殿星，等.距離多假目標干擾下雷達網優化選擇研究[J].電光與控制，2016(2)：36-41.

[12]趙艷麗，王雪松，王國玉，等.多假目標欺騙干擾下組網雷達跟蹤技術[J].電子學報，2007，35(3)：454-458.

[13]孫殿星，王國宏，涂三軍，等.基于雷達組網的低可觀測目標跟蹤技術研究[J].電光與控制，2016(4)：6-11.

[14]孫殿星，王國宏，賀達超，等.雷達組網抗距離-速度欺騙復合干擾技術研究[J].現代防御技術，2016，44(3)：84-98.

[15]BLACKMAN S, POPOLI R. Design and analysis of modern tracking systems[M]. London: Artech House, 1999.

[16]BLAIR W D, WATSON G A, KIRUBARAJAN T, et al. Benchmark for radar allocation and tracking in ECM[J]. IEEE Transactions on Aerospace & Electronic System, 1998, 34(4): 1097-1114.

[17]BORDONARO S, WILLETT P, BARSHALOM Y. Decorrelated unbiased converted measurement kalman filter[J]. IEEE Transactions on Aerospace & Electronic System, 2014, 50(2): 1431-1444.

[18]BAR-SHALOM Y, DAUM F, HUANG J. The probabilistic data association filter[J]. IEEE Control Systems, 2009, 29(6): 82-100.