轉角不對中轉子系統的電機電流特性

郭偉杰 ，楊兆建 ，石江波 ，李 峰

（1.太原理工大學 機械工程學院，山西 太原 030024；2.煤礦綜采裝備山西省重點實驗室，山西 太原 030024）

1 引言

轉子系統是旋轉機械的核心部件，而不對中是最為常見的故障之一，約占總故障的60%[1]，具有轉子不對中的系統在運行過程中易出現軸撓曲變形、機械振動、軸承早期磨損及油膜失穩等現象[2]，因此國內外學者關于轉子系統不平行故障的研究有很多。

轉子系統不對中故障可以分為平行不對中、轉角不對中和平行轉角不對中三種，而在實際工況中，一般二者兼而有之，或者以某種不對中故障為主出現。文獻[3]基于諧波平衡法分析了轉角不對中故障轉子系統的動力學模型，結果表明，系統不僅會產生與不平衡類似的工頻振動，而且也會產生工頻與轉子不對中角方向振動頻率倍數的組合頻率；文獻[4]建立了考慮電機聯軸器影響的雙盤不對中-碰摩耦合故障轉子系統力學模型和有限元模型，研究了碰摩剛度和不對中角度兩個重要參數對系統動力學特性的影響。文獻[5]通過對不對中轉子系統動力學響應的研究發現，平行不對中故障會激發出較強的一倍諧波分量，而高倍頻諧波較弱，而偏角不對中會激發出很強的三次諧波分量；文獻[6]建立了一個多跨轉子—軸承系統試驗臺，重點分析了平行不對中和交角不對中轉子的動力學特性和振動機理；文獻[7]使用等效不對中力矩和接觸理論研究了不同轉速下轉角不對中故障的轉子系統的動力學特性，并認為二倍頻比例值可作為含有不對中故障轉子系統故障嚴重程度的一個判斷依據。從以往的研究文獻中可以看出，大部分的文獻都是通過振動分析方法來研究轉子系統的不對中故障，而將電流分析方法（MSCA）應用到轉子系統的平行不對中故障的研究相對較少，而電流分析方法相對于振動分析方法具有信息集成度高、傳遞路徑短、信噪比高等優點[8]。

針對轉子系統轉角不對中故障，建立轉子系統動力學模型，推導出轉子系統的不對中力矩，并以電機的電磁扭矩為紐帶，在MATLAB/Simulink中建立轉子系統機電耦合仿真模型，對電機電流信號進行頻域分析，研究轉子系統在轉角不對中故障激勵下電機電流信號的耦合特性。

2 機電耦合模型

2.1 轉角不對中轉子系統動力學模型

單跨轉角不對中轉子系統示意圖，如圖1所示。假設將轉子系統簡化為質量分別為m1的單圓盤與彎扭柔性的無質量軸，并且轉軸各向同性，軸承為剛性支撐。轉子系統存在微小角不對中量α。轉角不對中力矩模型，如圖2所示。設電機的輸出扭矩為T，則由于轉角不對中故障的存在，則扭矩T可以分解為TS和Tz兩部分，TS和Tz分別為：

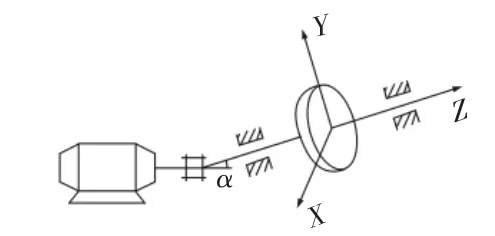
圖1 轉角不對中轉子系統示意圖Fig.1 Sketch of Rotor Systems with Angular Misalignment

圖2 轉角不對中力矩模型Fig.2 Moment Model of Angular Misalignment

由于負載轉矩的波動直接影響著氣隙扭矩，氣隙扭矩的變化通過定子磁通引起定子電流的變化[9]，因此我們只考慮繞Z軸的轉動，則：

式中：J—轉子系統的極轉動慣量，J=0.05kg·m2；φr—轉子的旋轉

角度，φr=ωrt+θr；θr—轉子的扭振角位移。

對于轉角不對中的轉子系統，利用歐拉公式可得其電機的轉動角速度與轉子系統的角速度將滿足下式的關系[10]：

式中：ωr—轉子的角速度，ωr=φ˙r；ωm—電機的角速度，ωm=φ˙m；φm

—電機的轉角，φm=ωmt+θm；θm—電機軸的扭振角。

將式（4）對時間進行求導可得：

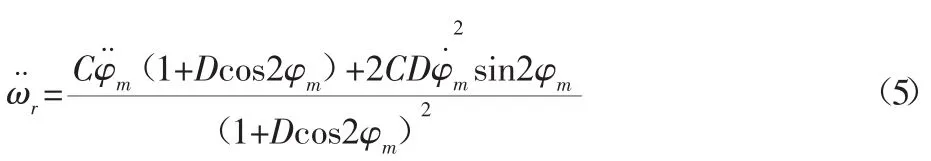
將式（5）代入式（3），得到轉子系統的不對中力矩為：

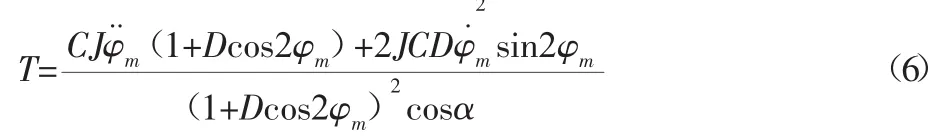
2.2 電機動力學模型

建立三相異步電機在αβo系統下的仿真模型，在αβo系統下電機的電壓方程為：

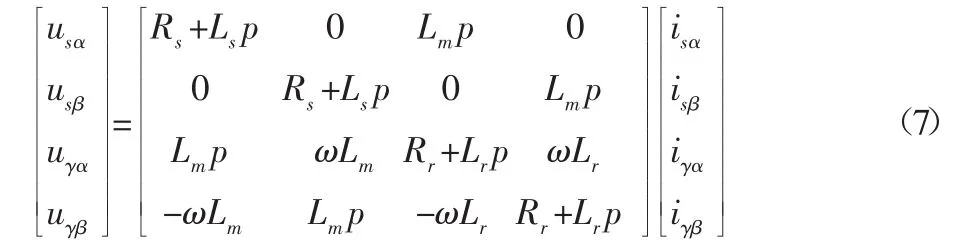
磁鏈方程：

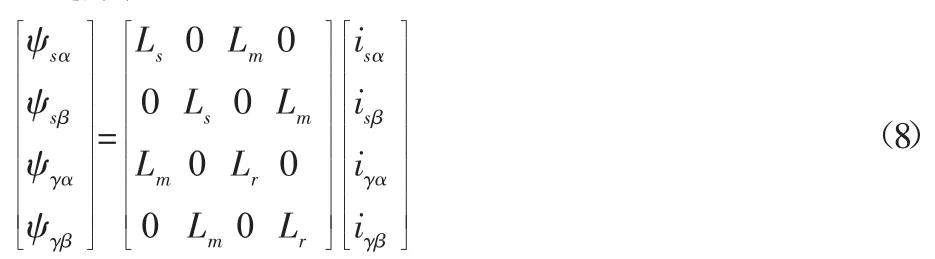
式中：ωm—電機轉動角速度；RS—定子繞組電阻；Rr—轉子繞組電阻；LS—定子繞組自感；Lr—轉子繞組自感；Lm—定轉子繞組互感；np—電極對數；Te—電磁轉矩；Mz—慣性扭矩與外扭矩之和；J0—電機的轉動慣量。

電機仿真參數如下：f=50Hz；RS=4.26Ω；Rr=3.24Ω；LS=0.666H；Lr=0.670H；Lm=0.651H；U=380V；J0=0.05kg·m2。根據式（6）～式（10）建立三項異步電動機—偏角不對中轉子系統的機電耦合仿真模型。

電磁轉矩方程：

運動方程：

3 機電耦合模型仿真分析

分別取轉子系統的轉速為750r/min、1500r/min、3000r/min，每個轉速下分別取轉角不對中量α為0°、1°、3°和6°，其電磁扭矩和電機電流的頻譜圖，如圖3所示。由圖可知，在α為0°時，電磁扭矩會激發出工頻偶數倍頻的諧波分量，而電流信號會激發出工頻奇數倍頻的諧波分量，當轉子系統存在轉角不對中后，電磁扭矩的2倍頻分量（100Hz）出現明顯的突變，而電流信號的3倍頻分量（150Hz）的峰值也出現增大的現象，并且隨著α的增大，其幅值也都明顯的增大。隨著轉子系統轉速的提高，電磁扭矩和電機電流的高倍頻諧波分量逐漸會被淹沒，而電磁扭矩的2倍頻分量和電流信號的3倍頻分量則更為明顯，因此可以將其作為轉子系統轉角不對中故障的一個判斷依據。

電磁扭矩的2倍頻峰值，如圖4所示。由圖可知，當轉角為0°時，電磁扭矩的二倍頻峰值隨著轉速的增大而變大，但是當轉子系統存在轉角不對中后，同一轉角不對中量下，轉速低的二倍頻峰值反而比較大；同一轉速下，峰值會隨著轉角不對中量的增大而增大。

電機電流信號的3倍頻峰值隨轉角不對中量的變化規律，如圖5所示。由圖可知，轉速為750r/min和1500r/min時，峰值變化基本相似，但是當轉速為更高為3000r/min時，在轉角0°＜α＜2°時，其峰值明顯比低轉速的高，但是當偏角不對中量繼續增大后，其峰值基本與低轉速的重合，即電機電流的3倍頻分量對轉子系統的轉角不對中量比較敏感，而對轉速并不太敏感。

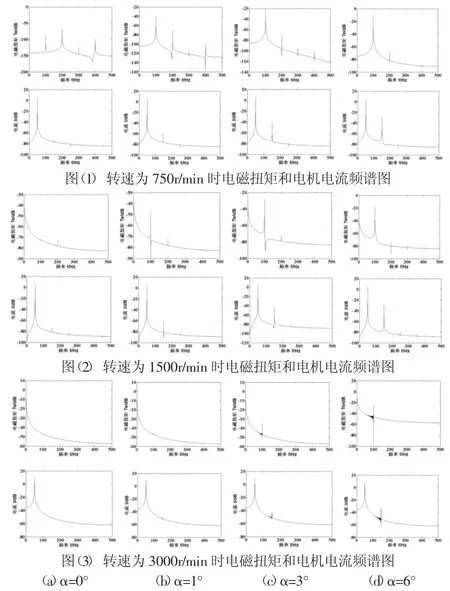
圖3 不同轉速下電磁扭矩和電機電流頻譜圖Fig.3 Frequency Spectrograms of Electromagnetic Torque and Current Signal at Different Speed

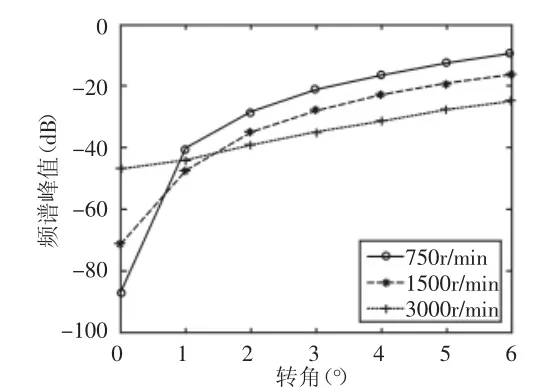
圖4 電磁扭矩的二倍頻峰值隨轉角不對中量的變化曲線圖Fig.4 Double Frequency Peak Graphs of Electromagnetic Torque with Change of Misaligned Angle

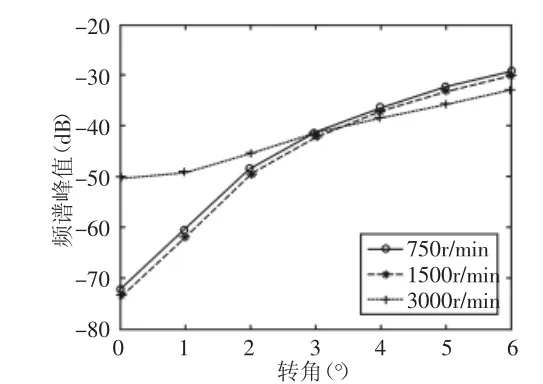
圖5 電機電流的三倍頻峰值隨轉角不對中量的變化曲線圖Fig.5 Three Frequency Peak Graphs of Motor Current with Change of Misaligned Angle

4 結論

通過建立轉角不對中轉子系統動力學模型，推導出轉角不對中力矩，然后以轉角不對中力矩和電機的電磁扭矩為紐帶，建立機電耦合仿真模型，并對得到的電磁扭矩信號和電機電流信號進行頻譜分析，得到以下結論：

（1）當轉子系統不存在轉角不對中故障的情況下，電磁扭矩會出現工頻的偶數倍頻的諧波分量，而電機電流信號會出現奇數倍頻的諧波分量。

（2）若轉子系統存在轉角不對中故障，則電磁扭矩的2倍頻諧波分量和電機電流的3倍頻諧波分量會出現突變，而且其峰值會隨著轉角不對中量的增大而增大。

（3）通過不同轉速下的對比分析可得，電磁扭矩的2倍頻分量和電機電流信號的3倍頻分量對轉子系統的轉角不對中故障更為敏感，而對轉速并不敏感，因此其可以作為轉角不對中故障的一個判斷依據。

［1］趙營豪，陳宏，朱朝鵬.轉子不對中定量研究［J］.機械設計與制造，2013（12）：109-110.（Zhao Ying-hao，Chen Hong，Zhu Chao-peng.Research on the quantitative of misalignment［J］.Machinery Design&Manufacture，2013（12）：109-110.）

［2］夏松波，張新江，劉占生.旋轉機械不對中故障研究綜述［J］.振動、測試與診斷，1998（3）：157-161.（Xia Song-bo，Zhang Xin-jiang，Liu Zhan-sheng.Survey of the research on coupling with misalignment of rotary machinery［J］.Journal of Vibration，Measurement&Diagnosis，1998（3）：157-161.）

［3］李明.轉角不對中故障的轉子系統非線性動力學特征［J］.振動、測試與診斷，2011，31（5）：552-556.（Li Ming.Nonlinear dynamics characteristics of rotor system with angular misalignment［J］.Journal of Vibration，Measurement&Diagnosis，2011，31（5）：552-556.）

［4］劉楊，太興宇，姚紅良.雙盤轉子軸承系統不對中-碰摩耦合故障分析［J］.振動、測試與診斷，2013，33（5）：819-823.（Liu Yang，Tai Xing-yu，Yao Hong-liang．Study on misalignment-rubbing coupling fault of dual-disk rotor-bearing system including the impact of motor coupling［J］.Journal of Vibration，Measurement&Diagnosis，2013，33（5）：819-823.）

［5］Patel T H，Darpe A K.Vibration response of misaligned rotors［J］.Journal of Sound and Vibration，2009，325（3）：609-628.

［6］李明，李自剛.聯軸器不對中故障轉子系統的動力學試驗［J］.振動、測試與診斷，2015，35（2）：345-351.（Li Ming，Li Zi-gang.Theoretical and experimental study on dynamics of rotor-bearing system with the faults of coupling misalignment［J］.Journal of Vibration，Measurement&Diagnosis，2015，35（2）：345-351.）

［7］劉楊，太興宇，趙倩.轉子系統不對中-碰摩耦合故障的動力學特性［J］.東北大學學報：自然科學版，2013，34（4）：564-568.（Liu Yang，Tai Xing-yu，Zhao Qing.Dynamics characteristics of misalignment-rubbing coupling fault for rotor system［J］.Journal of Northeastern University：Natural Science，2013，34（4）：564-568.）

［8］張克南，陸揚，謝里陽.基于SVD方法的弱故障特征提取方法［J］.機床與液壓，2006（10）：214-216.（Zhang Ke-nan，Lu Yang，Xie Li-yang.A New method for extracting the weak fault symptoms of current signal via SVD［J］.Machine Tool&Hydraulics，2006（10）：214-216.）

［9］張克南，陳一軍，謝里陽.電機電流分析法在機床類設備診斷中的應用研究［J］.機床與液壓，2007，35（3）：196-198.（Zhang Ke-nan，Chen Yi-jun，Xie Li-yang.Application of motor current signal analysis in fault diagnosis of machine tools［J］.Machine Tool&Hydraulics，2007，35（3）：196-198.）

［10］黃錫愷，鄭文維.機械原理［M］.北京：高等教育出版社，1989：157-216.（Huang Xi-kai，Zheng Wen-wei.Mechanical Principle［M］.Beijing：Higher Education Press，1989：157-216.）