概述解析“孿生素數猜想”之方法

貴州省務川中學 劉曉東 何長勇 申學勤貴州省務川縣實驗學校 王若仲

一 、方法的基本思路

以偶數18對應的情形為例說明這種基本思路，

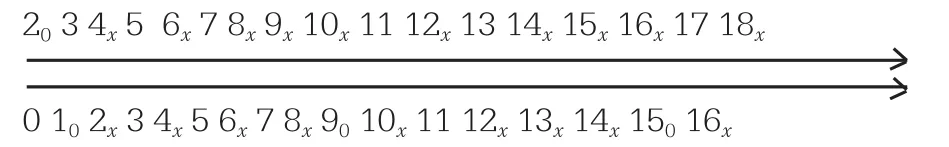
（1）在上軸中篩除所有合數及篩除下軸中它們分別對應的整數；

（2）在下軸中篩除所有合數及篩除上軸中它們分別對應的整數；

（3）在上軸中篩除整數2及篩除下軸中2對應的整數0，在下軸中篩除奇數1，篩除上軸中奇數1對應的整數3。

最后得出偶數2=5-3=7-5=13-11，還剩下2（對）。

根據這個思路，對于任一偶數2m（m≥3）對應的情形則有：

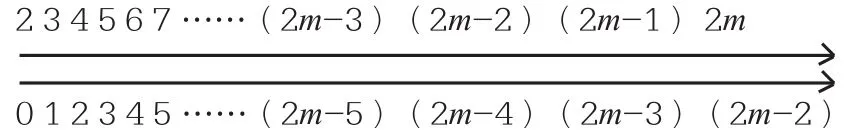
（1）在上軸中篩除所有合數及篩除下軸中它們分別對應的整數；

（2）在下軸中篩除所有合數及篩除上軸中它們分別對應的整數；

（3）在上軸中篩除整數2及篩除下軸中2對應的整數0，在下軸中篩除奇數1，篩除上軸中奇數1對應的整數3。

根據這個思路，證明存在偶數M（M＞2m），經過篩選后，M對應的情形中至少是增加了1對，增加的這1對就是孿生素數。

二、奇合數和奇素數的特性(初等數論13頁)

（1）對于任一較大的正整數M，設奇素數p1，p2，p3，…，pt均為不大于的全體奇素數（pi＜pj，i＜j，i、j=1，2，3，…，t），那么在區間中任何一個奇合數a，奇合數a均能被集合{p1，p2，p3，…，pt}中某一個奇素數pi（i=1，2，3，…，t）整除。

（2）對于任一奇數M（M≥9），設奇素數p1，p2，p3，…，pt均為不大于的全體奇素數（pi＜pj，i＜j，i、j=1，2，3，…，t），若奇數M均不能被集合{p1，p2，p3，…，pt}中的任一奇素數pi（i=1，2，3，…，t）整除，則奇數M為奇素數。

三、方法的基本步驟

（1）奇合數和順篩及上軸和下軸

奇合數為既是奇數又是合數的正整數，如：15，21，35等，這樣的奇數統稱為奇合數。

順篩就是兩千多年前的埃拉托斯特尼篩法(初等數論16頁)。

平面上兩條平行且方向均向右的數軸，上軸為上一條數軸，下軸為下一條數軸。

（2）構建篩選數學模型

對于任一偶數2m（m≥3），把它看成是由一條上軸與一條下軸平行且呈軸對稱的一個平面圖形， 這樣就構建了一個篩選數學模型。如下圖：

（3）數學模型篩選原則

數學模型篩選原則：在上軸中篩除某些整數，這些整數在下軸中分別對應的整數也跟著篩除；在下軸中篩除某些整數，這些整數在上軸中分別對應的整數也跟著篩除。

（4）利用數學模型進行篩選

把上軸中一個整數a和在下軸中與之對應的整數b稱為一對（組）。對于正實數x，符號〔x〕記為不大于x的最大正整數(十章數論50頁)。

對于偶數2m（2m=W），設素數p0，p1，p2，p3，…，pt均為不大于偶數2m的全體素數（pi＜pj，i＜j，i、j=0，1，2，3，…，t），t∈N。那么偶數2m對應的篩選數學模型，如下圖：

為了便于分辯，改為如下圖：

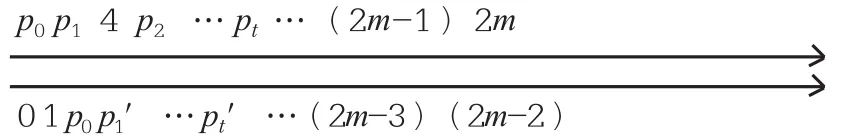
其實p1=p1′，p2=p2′，p3=p3′，…，pt=pt′。在上軸中篩除q的倍數與在下軸中篩除q的倍數是不等同的。若轉換到篩除對數上來分析，上軸上的情形和下軸上的情形要區別分析計算。

按照篩選原則篩選：

（1）在上軸中篩除偶素數p0的所有倍數，下軸中的全體偶數一同被篩除，篩選后則剩下：W-〔W÷p0〕=W（1-1÷p0）（對）。

（2）在上軸中篩除奇素數p1的所有倍數及篩除下軸中它們分別對應的整數，再篩選后剩下：W-〔W÷p0〕-〔W÷p1〕+〔W÷（p0p1）〕。其中，〔W÷p0〕與〔W÷p1〕，W減〔W÷p0〕時，〔W÷（p0p1）〕已減了一次，減〔W÷p1〕時，〔W÷（p0p1）〕又減了一次，故要返回一次。

（3）在下軸中篩除奇素數p1′的所有倍數及篩除上軸中它們分別對應的整數再篩選后剩下：W-〔W÷p0〕-〔W÷p1〕+〔W÷（p0p1）〕-〔W÷p1′〕+〔W÷（p0p1′）〕=W-〔W÷p0〕-2〔W÷p1〕+2〔W÷（p0p1）〕≈〔W（1-1÷p0）（1-2÷p1）〕（對）。減〔W÷p1′〕時，〔W÷（p0p1）〕多減了一次，又要返回一次。

（4）在上軸中篩除奇素數p2的所有倍數及篩除下軸中它們分別對應的整數；在下軸中篩除奇素數p2′的所有奇數倍及篩除上軸中它們分別對應的奇數，再篩選后剩下：W-〔W÷p0〕-〔W÷p1〕+〔W÷（p0p1）〕-〔W÷p1′〕+〔W÷（p0p1′）〕-〔W÷p2〕-〔W÷p2′〕+〔W÷（p0p2）〕+〔W÷（p1p2）〕+〔W÷（p1′p2）〕+〔W÷（p0p2′）〕+〔W÷（p1p2′）〕+〔W÷（p1′p2′）〕-〔W÷（p0p1p2）〕-〔W÷（p0p1′p2）〕-〔W÷（p0p1p2′）〕-〔W÷（p0p1′p2′）〕=W-〔W÷p0〕-2〔W÷p1〕+2〔W÷（p0p1）〕-2〔W÷p2〕+2〔W÷（p0p2）〕+4〔W÷（p1p2）〕-4〔W÷（p0p1p2）〕≈〔W（1-1÷p0）（1-2÷p1）（1-2÷p2）〕（對）。

（5）在上軸中篩除奇素數pt的所有倍數及篩除下軸中它們分別對應的整數，在下軸中篩除奇素數pt的所有倍數及篩除上軸中它們分別對應的整數，最后剩下：W-〔W÷p0〕-2〔W÷p1〕+2〔W÷（p0p1）〕-2〔W÷p2〕+2〔W÷（p0p2）〕+4〔W÷（p1p2）〕-4〔W÷（p0p1p2）〕-2〔W÷p3〕+2〔W÷（p0p3）〕+4〔W÷（p1p3）〕+4〔W÷（p2p3）〕-4〔W÷（p0p1p3）〕-4〔W÷（p0p2p3）〕-8〔W÷（p1p2p3）〕+8〔W÷（p0p1p2p3）〕-2〔W÷p4〕+…-2〔W÷pt〕+2〔W÷（p0pt）〕+4〔W÷（p1pt）〕+4〔W÷（p2pt）〕+4〔W÷（p3pt）〕+…+4〔W÷（pt-1pt）〕-4〔W÷（p0p1pt）〕-4〔W÷（p0p2pt）〕-…+（-1）t-12t〔W÷（p0p1p2p3…pt-1pt）〕≈〔W（1-1÷p0）（1-2÷p1）（1-2÷p2）（1-2÷p3）…（1-2÷pt-1）（1-2÷pt）〕（對）。

四、判別孿生素數無窮多

對于前面闡述的篩法，在轉換到計算篩除對數時，有兩種情形被計算多篩除了：

（1）在素數p0，p1，p2，p3，…，pt之中存在的孿生素數被全部計算篩除了。

（2）“上軸中的奇合數-下軸中的奇合數=2”的情形被重復計算了。

就是計算篩除多了。也影響不到判別孿生素數無窮多。

現假定孿生素數只有有限多，不妨設相當大的素數pt之后不存在孿生素數，

根據奇合數和奇素數的特性，可設偶數2m=pt2+1，則素數p0，p1，p2，p3，…，pt均為不大于的全體素數（pi＜pj，i＜j，i、j=0，1，2，3，…，t），t∈N。根據前面的篩法情形，則有Y=〔2m（1-1÷p0）（1-2÷p1）（1-2÷p2）（1-2÷p3）…（1-2÷pt-1）（1-2÷pt）〕。因為有下列兩種情形被計算多篩除了：

（1）在素數p0，p1，p2，p3，…，pt之中存在的孿生素數被全部計算篩除了。

（2）“上軸中的奇合數-下軸中的奇合數=2”的情形被重復計算篩除了。

這樣我們就可以得出結論：假定孿生素數只有有限多不能成立。

[1]閔嗣鶴，嚴士健．初等數論[M]．北京：人民教育出版社，1983（02）．

[2]戎士奎．十章數論[M]．貴陽：貴州教育出版社，1994（09）．