初中數學數形結合思想的教學設計研究

祝春玲

[摘? 要] 本文以“數形結合”為主題，通過分析，闡述數形結合的教學原則與教學策略，提出初中數學數形結合思想的教學設計思路，以期給廣大教師帶來有價值的參考.

[關鍵詞] 數形結合;數學課堂;策略

數形結合的教學原則

1. 數學語言的靈活轉換

“數”與“形”，在某種環境與條件下，它描述的是同一個數學問題，同一種數學現象，所指向的是同一個板塊的數學主題，這也是“數形結合”思想的由來，用數字/數據與圖形來同時表達某一個數學原理. 因此，教師在指導學生認識與理解“數形結合”這一思想時，首先要秉承數學語言靈活轉換這一原則.

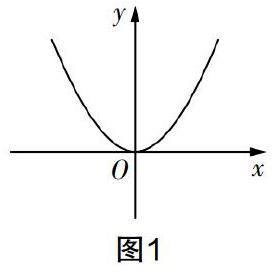
以“二次函數”為例，在“二次函數y=ax²（a≠0）的圖像和性質”這一知識點中，函數“y=ax²（a>0）”的圖像如圖1.

這也就意味著這一個函數表達式與這一個函數圖像，兩者都表達了同樣的內容. 學生在書寫表達式時，應當可以靈活地畫出它所對應的圖形. 與此同時，當學生看到這一圖形時，也可以準確地寫出它所反映的函數表達式. 因此，“數學語言的靈活轉換”這一教學原則的目的在于培養學生的數學敏感性，能夠對同一個數學知識保持著“數”和“形”的雙重認知，這是學生后續真正運用“數形結合”這一思想的基礎.

2. 抽象問題的具化呈現

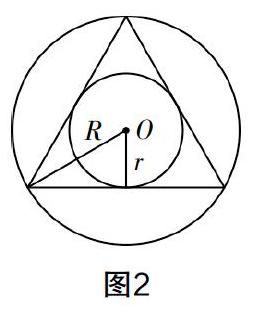
“數形結合”要解決的根本問題就是認知問題，不論是借助數字來理解圖形，還是借助圖形來理解數字，其目的都在于讓問題變得更加清晰和直觀. 因此，教師在指導學生認識與理解“數形結合”這一思想時，第二個要秉承的原則就是“抽象問題的具化呈現”. 比如在圖2中，假如僅知道正三角形的邊長為a，如何求解它的內切圓與外接圓組成的圓環的面積呢？

假如學生用常規的思想，想通過求解外接圓和內切圓的面積再相減，顯然題目給予的條件并不充分. 在這種情況下，學生就需要將求解“兩個圓的面積相減”的問題轉化成求出“兩圓的半徑平方差”這一問題. 如此一來，假如我們將正三角形外接圓、內切圓的半徑和面積分別設為R，r，S₁，S₂，那么圓環的面積就等于S_1-S₂=πR²-πr²=π（R²-r²）. 顯然，題目可以求解. 這一求解思路體現的是“數形結合”中的“以形助數”和“以數助形”. 當教師能夠引導學生在看到復雜的、抽象的問題時，巧妙地利用數形結合來使其變得簡單與具體，那么數學問題自然也會迎刃而解.

3. 數學規律的摸索抓取

教師在組織開展“數形結合”的教學時，還應當秉承指導學生進行數學規律的摸索與抓取的原則. 數學是一門內在邏輯性非常強的學科，各個知識板塊看似彼此獨立，但這中間卻有著千絲萬縷的關系. 而學生在解答題目時，也會發現同一個知識點可能會被不同的題目與不同的問法所呈現，這就要求學生能夠抓住海量題目中的相似規律，這也是數形結合思想的重要出發點. 假如學生能夠將生活中的某一種現象或某一個問題，通過數形結合的思想來將隱藏其中的規律抓出來，無疑對問題的解決有著很大的幫助. 而借助數形結合的思維與方法來變現象為規律，也是我們在教學中經常強調的要讓學生真正地理解知識，而不是機械地“刷題”.

數形結合的教學策略

1. 對應關系的搭建——邏輯列舉法

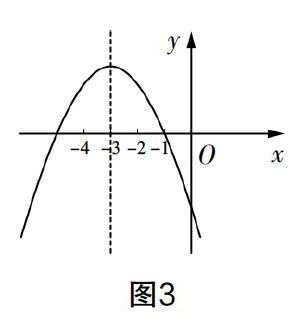
數形結合的出發點在于用“數”和“形”來表達同一個數學問題. 因此，教師在將這種思想與工具教給學生時，可以采用邏輯列舉法這一教學策略來讓學生學習搭建“數”與“形”之間的對應關系. 邏輯列舉法的本質在于讓學生理順數學知識點在“數”與“形”兩者的呈現方式，并將兩者之間的脈絡打通. 比如二次函數“y=-1/2x²-3x-5/2”，假如教師要學生說出x為何值時，y會隨x的增大而增大？x為何值時，y會隨x的增大而減少？顯然，單純地看這一函數，學生能想到的最常用的方式就是通過多次“賦值代入法”來進行驗證，但這種方法耗時長，對驗證的次數有最低要求. 面對這種情況，數形結合這一工具就能派上用場. 教師可以指導學生通過描點法來繪制其圖像，如圖3.

借助這個圖像，我們能夠很明顯地得知，當x<-3時，函數y隨著x的增大而增大;當x>-3時，函數y隨x的增大而減少. 不僅如此，我們還可以從圖像上得知函數與x軸的交點坐標以及與y軸的交點坐標等.

將這個圖像與二次函數“y=ax²+bx+c（a，b，c是常數，且a<0）進行對比，會發現兩者在輪廓上大體相似，但具體位置不同，這其實是拋物線的平移問題，而這一平移規律的背后邏輯是：一般地，拋物線y=a（x-h）²+k與y=ax²形狀相同，位置不同. 把拋物線y=ax²向上（k>0）或向下（k<0）平移k個單位;再向左（h<0）或者向右（h>0）平移|h|個單位，就得到y=a（x-h）²+k的圖像. 簡單點講就是“左加右減括號內，號外上加下要減”. 當學生把這一邏輯原理抓出來后，與此類知識點有關的數學問題，就可以自然地運用數形結合來思考. 總的來講，邏輯列舉教學法強調的是讓學生能夠將“數”與“形”相互關系背后的邏輯抓住，以準確地把握數形轉化的規律.

2. 數學模型的設計——主題任務法

上面提到，教師在進行“數形結合”這一思想與工具的教學時，要指導學生秉承化抽象為具體的原則，為了實現這一教學目的，教師可以采用主題任務教學法來指導學生嘗試設計數形轉化的模型. 以“三角形”為例，比如“三角形的高、中線與角平分線”這個知識點，教師可以讓學生圍繞著這個知識點來思考直角三角形、銳角三角形、鈍角三角形這三種不同三角形中高、中線與角平分線的關系與聯系. 最終大家在課堂上經過討論分析后，分別繪制出了如圖5～圖7的三個圖形.

可以看出：銳角三角形的三條高在三角形內部，相交于一點，如圖5所示. 直角三角形有兩條高與直角邊重合，另一條高在三角形內部，它們的交點是直角頂點，如圖6所示. 鈍角三角形有兩條高在三角形外部，一條高在三角形內部，三條高不相交，但三條高所在直線相較于三角形外一點，如圖7所示. 這三個三角形就是三種高、中線、角平分線的模型. 當學生下次再遇到類似的題目時，就可以把抽象的空間概念具化為這三種模型，并借助模型特點來解答對應的題目. 總的來講，主題任務法強調的是學生能夠為“數”與“形”的相互轉化找到特定的載體.

3. 實際問題的解決——案例模擬法

學習的初衷是為了解決問題，因此，“學以致用”一直都是我們在教學時所要強調的原則. 基于此，教師在進行“數形結合”思想的教學傳授時，可以采用案例模擬法這一教學策略來提高學生的問題解決能力. 以“一次函數”為例，假如有一道題目是這樣的：“某水利工地派48人去挖土和運土，如果每人每天平均挖土5方或運土3方，那么應該怎樣分配挖土和運土的人數，正好能夠使挖出的土及時運走？”這就是一個實際問題，是數學問題在生產中的運用. 它需要學生列出方程組后用圖像法來求解. 假如將應分配挖土的人數設為x，運土的人數設為y，則根據題目可以列出方程組x+y=48，5x=3y， 繪制出的圖像如圖8.

受限于篇幅，筆者這里不在解題步驟上多加陳述，但這一題目折射的就是一次函數與二元一次方程組的關系. 顯然：從“數”看，求解方程組和求解自變量為何數值時函數值相等，這一對關系指向的是同一個問題;從“形”看，方程組的解和兩直線交點的坐標，這一對關系指向的也是同一個問題. 這就是數形結合思想在具體生產問題中的體現. 總的來講，案例模擬法強調的是學生能夠切實地將理論遷移到實踐中，將數形結合思想真正地掌握與運用.

結語

在眾多的數學思想中，“數形結合”無疑是最普遍、使用頻率最高的思想. 它指的是將數學語言中的數字與圖形（或某種有意義的符號）結合在一起來思考問題、判斷問題. 作為一種基本且重要的數學思想，它在培養學習者數學思維上具有非常重要的影響與作用. 為了更好地實現這一教學目的，教師在設計數學課堂時，應當尊重“數形結合”的思維規律，并以此為參考基礎作為教學原則. 同時采取邏輯列舉法、主題任務法、案例模擬法等來將教學目標執行到位，讓學生在學習的過程中能夠逐步地認識并掌握“數形結合”，以提高學生的學習效率與學習質量.