電力用戶節能減排因素相關性分析

何海航 邵鵬 奚鵬飛 賈詩樂 霍現旭 宋杰

摘要

隨著能源資源越來越緊張和人們對環境保護意識的增加，節能減排越來越得到了大家的廣泛關注。為了有效的展現出節能減排的成果，文章中采用了幾組較為典型且具有代表性的相關指標。相關的指標數量十分巨大，處理起來十分繁瑣，故我們采用了主成分分析法。在原先的指標中，篩選出具有代表意義的少量的主成分，有效降低了變量維數而又不造成信息的大量丟失。最后以某一地區為例進行主成分分析，分析了該地區電力用戶的節能減排相關因素。

【關鍵詞】主成分分析 節能減排 相關性分析

節能減排是指節約能量資源，降低能源消耗、減少污染排放。我們是這樣來對節能進行定義的：通過符合技術要求，具有經濟性，有利于社會環境的方法，在社會生產和能源利用的過程中，合理地利用能源，減少浪費以及污染排放。從定義上來看，節能減排最重要的內容就是節約能源和提高能源利用效率。

在電力利用的整個過程中都貫穿著節能減排。從電力的生產，傳輸到最后的給每個用戶的分配環節，都應采取經濟的切符合技術要求的方法，來減少浪費提高電利用效率1995年后國際上更廣泛地采用“能源效率”（energyefficiency）一次來代替“節能”（energyconservation）一詞·實質上，二者涵義是一致的。

而在節能減排的過程中，電力用戶是十分關鍵的對象之一。在用電時，電力用戶對于資源的使用情況以及對于污染物的處理能夠很好的展現他們對于能源的利用狀況和能源自身性質。而從另一個方面來說，對于能源的使用情況同樣表明了用戶在于用電過程中尚存在一些問題。要正確把握這一系列的問題，就可以規劃出相應的方法來加以解決，以此來達到節能減排的目的。

根據上面所述，評價電力用戶的節能減排效果會涉及到大量的指標。但是，這大量的指標中不可避免的存在著許多的重復性和相關性。這會使得最后的統計提升許多復雜度。而為解決這一問題，最直觀和簡單的方法就是減少變量的數量。但這也會造成很大的弊端，即信息的缺失和不完整。此時我們采取主成分分析法，它可以在保證信息完整的前提下，減少變量的個數。因此，本文對于節能的各個指標將采取主成分分析法來獲取其中的關鍵性代表性指標，以此來描述和分析用戶的節能減排情況。

1 主成分分析法

從數學的角度上來說，主成分分析的作用是降低數據的維度。從根本上來說，它將互相相關的p個指標X=[X₁，X₂，…，X_p]，對它們進行重組從而可以獲得全新的綜合指標F_m。這組指標相對來說個數較少而且兩兩不想關，可以代替原來大量的指標。當然，在這個重組過程中，有亮點值得注意。一是要保證原來指標信息的完整性。二是要確保新獲得的指標互相之間不想關，即保證所得的信息沒有重疊。

假設由重組后所得到的新的綜合指標為：

我們知道，為了描述所得指標對于信息描述的完整程度，我們可以求其方差。方差越大，信息也就越完整。

我們在此將所得的p個線性組合中方差最大的定義為第一主成分，假設是F₁，那么它所包含的信息是最大的。同理我們可以得到第二主成分，假設其為F₂。為了保證上文所提到的信息沒有重疊，F₁與F₂之間應該互不相關，在數學上即要使得Cov（F₁，F₂）=O，所以在p個原變量的所有線性組合中，F₂是和F₁互不相關的且方差也是最大的。同理可得出原變量指標x₁，x₂，…，x_p的第1、第2、……、第m個主成分F₁，F₂，……，F_m（m≤P）。

最終的目的是求出所有的主成分，因此需要確定每個主成分關于原變量的關系式。也就是要確定表達式中的系數a_ij（i=1，2，…，m;j=2，…，p）。而在實質上，主成分的方差可用原變量協方差矩陣特征根來表示。原變量協方差矩陣為：

其中：

通過上述的分析可以得出，主成分的方差值不用直接求出，而是可以用它們特征根中的較大的那個來代替。同時，這些特征根對應的特征向量可以表征主成分的系數α_i。假設前m個較大的特征值為λ₁≥λ₂≥…λ_m>0，α_i為特征值λ_i對應的單位特征向量，則主成分F_i的關于原變量的系數為α_i。因此，則原變量的第i個主成分F_i為：

F_i=α_iX（5）

對于所求的方差將其求和，所得的和值可以表示總的信息量。那么每一個主成分所包含的信息量我們可以通過其方差的貢獻率來表示。我們定義α_i為：

總的來說，若是主成分的貢獻率高于一定值，一般地，我們將其設為85%。那么我們稱這一組主成分可以較為完整地給出原變量的信息。據此，可以反映原變量信息的主成分的數量也可以確定下來。如果說現有m個主成分，它們方差的累計貢獻率G（m）為：

當獻率G（m）大于等于85%時，最終必要的主成分數量就是m。接下來，就是計算主成分載荷。它表征了主成分和原變量的相關程度。原變量x_j（j=1，2，…，P）在主成分F_i（i=1，2，…，m）上的荷載l_ij（i=1，2，…，m;j=1，2，…，p）：

我們能夠通過SPSS軟件來得出主成分載荷矩陣。其中，主成分載荷矩陣即為“成分矩陣”。通過該矩陣，能夠分析出哪些因素是與用戶節能減排聯系最為緊密的。

2 用戶節能減排指標

在本文中，為了能夠較為精準的反映電力用戶的節能減排情況，我們選取了一系列極具代表性的典型的指標，通過這些來正確評價節能減排的效果。具體的指標如下：

（1）單位產值能耗比率X1：電力用戶增加單位產值所消耗的電力（kWh/yuan），反應電能在使用時的效率高低。

（2）單位產品用電量x₂：單位產品在被用戶生產時所需要的電能總量（kWh），反應在生產過程中，電能的實用效率。

（3）載容比x₃：所需的最大電能與報裝容量的比值，反應報裝容量是否滿足需求。

（4）負荷率x₄：在用電的所有時間段中平均負荷與最大負荷的比值，反應在使用電能時，時間安排和分配是否合理。

（5）峰谷比x₅：低谷時間段所用的電量在全部時間段內所用電量中所占的比值，反應電力用戶用電時間的合理程度。

（6）功率因數x₆：用電時所產生的有功功率和視在功率比值，反應用電設備的運行是否良好。

（7）廢水排放量x₇：生產單位產品時，廢水排放量（kg/10⁶yuan），反應減少廢水排放的效果。

（8）廢氣排放量x₈：生產單位產品時，排放廢氣的量（m³/10⁶yuan），反應減少廢氣排放的效果。

（9）固體廢棄物x₉：生產單位產品時，排放固體廢棄物的量（kg/10⁶yuan），反應減少固體廢棄物排放的效果。

3 算例

通過一定的調查研究，現在以某地區為例，對這個區域內各個電力用戶企業在用電時的節能減排情況進行了分析。對于統計過的數據初步整理后，最終獲得了8個有效的用戶數據，如表1所示。

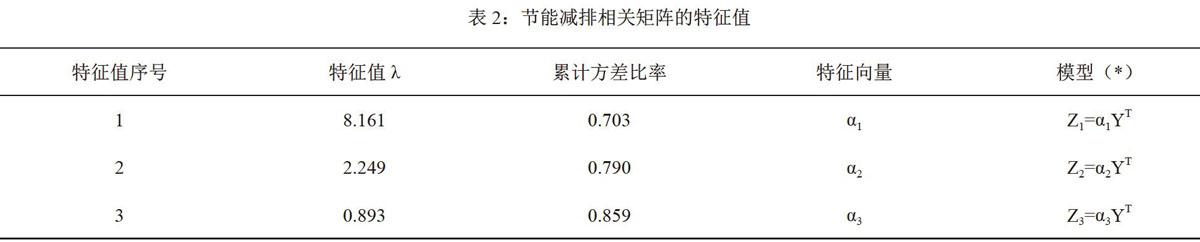
通過矩陣形式x=[x₁，x₂，…，x₉]編制了電力用戶節能減排的相關數據。在分析數據前，首先要對其實施標準化處理。這是因為若是方差很大或者維度不同，會造成無法確定因子負荷。對于數據進行進一步的處理后，構造相應的數據矩陣并計算其列向量相關系數矩陣R=[r_ij]_9×9（i，J -1，2，…，9），其中r_ij是第i個指標與第j個指標之間的樣本相關系數，并進一步由R的特征方程|R-λI₉|=0計算出其特征值λ_i（i=1，2，…，9）。經過計算，結果見表2。因為前三個主成分的累計貢獻率已經超過了85%，因此表2只給出了這相對應的3個特征值。

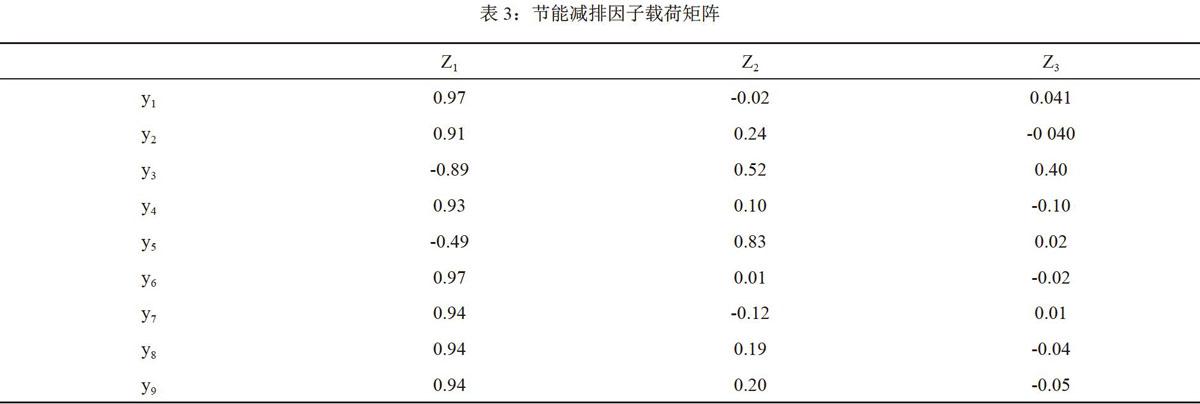
利用SPSS軟件獲得因子載荷矩陣。

從表3結果可以得到，Z₁到Z₃這三個主成分的信息完整度較高。第一主成分與許多參數相關，其中與載容比、負荷率、功率因數、峰谷比的關系最為密切。它綜合地包含了用戶選擇用電方式時所要考量的各方面的因素，并對用戶的用電能力有著重反應。第二主成分包含了企業用電時對環境因素的考量，與廢氣排放量、廢水排放量、固體廢棄物有很大關聯。第三主成分表現了企業生產過程中的效率，其與單位產品用電量和單位產值能耗比率相關聯。綜上分析，要想進一步實現節能減排，電力企業應當主要從改善對于電能的使用方式，有效地減少浪費和廢水廢氣和廢棄物的排放以及通過技術層面提高生產效率這三方面來入手。

4 結論

為了降低因考量因素太多而帶來的分析用戶節能減排效果的復雜性，本文使用了主成分分析法以此來減少變量，便于分析，并能保證不丟失信息，確保信息的完整度。在使用了主成分分析的方法后，根據電力用戶在用電時的特點，選取一些典型的能代表電力用戶減排效果的相關指標，然后通過成分分析法篩選出相關性較強的主要因素。最后選取了某地區的一些企業，以他們為例，研究了它們的減排效果。從結果來看，這些電力企業應當主要從改善對于電能的使用方式，有效地減少浪費和廢水廢氣和廢棄物的排放以及通過技術層面提高生產效率這三方面來入手。

參考文獻

[1]趙建安，金千致，魏丹青.我國主要工業部門技術節能減排的潛力及實現途徑探討[J].自然資源學，2012，27（06）：913-921.

[2]歐陽培.節能減排的現狀分析及其路徑選擇[J].再生資源與循環經濟，2008，8（01）：18-21.

[3]楊同宇，陶揚.節能減排：意義、途徑和策略[J].生態經濟，2008，1：273-276.

[4]王華，王連華，葛嶺梅.主成分分析與BP神經網絡在煤耗氧速度預測中的應用[J].煤炭學報，2008，33（08）：920-925.

[5]李靖華，郭耀煌.主成分分析用于多指標評價的方法研究——主成分評價[J].管理工程學報，2002，16（01）：39-43.

[6]余錦華，楊維權.多元統計分析與應用[M].廣州：中山大學出版社，2005：193-197.

[7]亞洲開發銀行.節能評價指標體系的設計與應用[M].北京：海洋出版社，2011：34-51.

[8]楊華峰，姜維軍.企業節能減排效果綜合評價指標體系研究[J].工業技術經濟，2008（10）：55-58.

[9]王彥彭.我國節能減排指標體系研究[J].煤炭經濟研究，2009（02）：31-39.