多節點協同任務分配問題的解決和驗證

張家良 王迎磊 李復名 周濤

摘要

針對多節點協同任務分配問題，將多節點執行任務的目標價值毀傷函數和代價函數作為目標函數，多節點協同任務分配問題等效為多目標函數優化問題，并建立多節點協同任務分配模型。在粒子群算法的基礎上，通過結合遺傳算法的交又和變異操作，提高了算法的局部搜索能力。對多節點協同任務分配問題進行求解得到非劣解集，為指揮決策者提供更多的信息依據，提高了多節點協同作戰能力。最后通過仿真計算對算法的有效性和收斂性進行了驗證。

【關鍵詞】多節點 任務分配問題 粒子群算法遺傳算法

1 引言

隨著以信息技術為核心的軍事科學技術迅速發展，軍事領域的各個方面發生了根本性的變革，這些變革推動了軍事領域通信速度、反應速度和作戰效率的極大提升。國外研究機構提出了一種全新的作戰理論——網絡中心戰。通常來說，連入網絡中心的各作戰單元稱為節點，網絡中心戰為各節點提供以信息利用和共享為顯著特征的優勢。而隨著作戰任務的日益復雜，傳統的作戰單元往往都是單獨對抗，難以滿足現代戰爭的需求。因此，多節點協同作戰是未來戰爭體系中的重要組成部分。但由于戰場環境，若多節點協同作戰時沒有對任務的預分配，不僅會使整個作戰效率低下，也會浪費作戰系統的資源。多節點協同作戰有以下的優勢：

（1）多節點協同作戰時，不再只是關注于單個節點的能力，而是通過節點的協同運用，充分利用各個節點的優勢，實現作戰效能的整體提升。

（2）多節點協同作戰時，若出現某些節點損傷或無法繼續執行任務的情況，其執行的任務可由其余尚有能力的節點執行。充分利用了協同作戰的優勢，具有一定的自我調節能力。

（3）多節點協同作戰時，對于在功能上以及時間上都有要求的復雜任務，多節點協同作戰能利用自身各個節點的功能性不同，完成不同的任務，并得到較高的效能。

因此，多節點協同作戰是未來戰爭的主要形式，而多節點協同任務分配問題直接影響作戰效能。為了滿足現代戰爭的需求，如何在各種約束條件下，給出任務分配方案，已經是當前重要的研究方向。

目前，國內外學者已經運用整數規劃、遺傳算法、粒子群算法、蟻群算法等對多節點任務分配問題進行了求解。文獻[7]基于整數規劃對多無人機任務分配問題進行建模，能有效處理復雜的約束條件。文獻[12]綜合考慮無人機的偵察、攻擊、隱身和武器掛載能力，通過將各因素加權求和的方式構建單目標優化模型，對任務分配問題進行求解。文獻[13]對編碼方式和約束滿足進行了改進，成功應用在任務分配問題的求解中。本文將多節點執行任務的目標價值毀傷和代價兩個關鍵指標作為目標函數，建立多目標優化模型，采用混合粒子群算法求解任務分配方案集。

2 多節點協同任務分配問題

為了直觀地描述多節點協同任務分配問題，本文假設多節點執行對目標的打擊任務。通過引入多節點執行任務的目標價值毀傷和代價兩個目標函數，將多節點協同任務分配問題等效為多目標函數優化問題。多目標優化問題的目標函數之間彼此制約，目標函數不能被同時優化到極值。因此，本文引入非劣解和非劣解集概念。在多目標優化問題中，存在一個解，在解集中，已找不到每個目標函數都更優的其他解，那么該解稱為非劣解。包含非劣解的解集就是非劣解集。

2.1 多節點協同任務分配模型

假設由N個節點對M個目標執行打擊任務。定義分配矩陣X^N×M，其中各個元素的定義為x_i，j^k∈{0，1}，具體定義如下：多節點協同任務分配數學模型為：

其中J₁（x）為目標價值毀傷函數，J₂（X）為代價函數，由損耗代價函數和航程代價函數構成。具體定義如下：

以上公式中S_ij為第i個節點對目標j的殺傷概率，K_j表示第i個節點對目標j執行任務后的存活概率，Z_ij表示目標j的自身價值，L_ij表示執行任務的路程，L_ijmax表示執行任務的最大路程。ω₁和ω₂是損耗代價函數和航程代價函數的權重比值。

根據多節點協同任務分配模型，應當滿足以下約束條件：

約束條件分別表達了：

（5）決策變量x_ij為0時代表不打擊，x_ij為1時代表打擊;

（6）每個目標只能被攻擊一次;

（7）每個節點執行兩次打擊任務;

（8）執行任務后的目標價值毀傷不應大于目標的總價值;

3 混合粒子群算法

粒子群算法起源于對鳥群捕食行為的觀察和研究。粒子群算法用沒有質量和體積的粒子來模擬捕食的鳥，每個粒子通過速度以及位置更新從而使得粒子貼近個體極值和群體極值，從而使得整個群體達到最優，盡管操作相對容易，可以迅速求解問題，但在算法進行過程中，各個粒子會變得類似，可能導致算法只得到局部最優解。因此，本文采用混合粒子群算法，結合遺傳算法的優點，通過粒子與粒子極值兩兩交叉以及粒子自身變異的方式使其能探索到新的搜索空間，從而使得算法的局部搜索能力增強。

3.1 編碼方式

在混合粒子群算法中，尋求一個合適的表達方式，將粒子和任務分配方案對應是多節點任務分配中的關鍵。本文采用整數編碼方式來表達，每個粒子即是任務分配問題的一個方案，粒子的編碼長度即為目標數量，粒子編碼即為多節點序列對應的目標序列，表示一個任務分配方案。例如節點數目為4個，目標數量為8個。如表1所示，第1個節點對應目標4和目標1，第2個節點對應目標3和目標7，第三個節點對應目標5和目標6，第四個節點對應目標2和目標8。個體編碼即為[43521768]。

3.2 篩選非劣解集

篩選非劣解集分成兩類。第一類是在初始化后得到非劣解集，種群初始化后，計算各個粒子的兩個目標函數值。若對于某個解，在解集中，不存在目標函數值都更優的其他解，則將這個解篩選進非劣解集中。第二類是在算法每次迭代后更新非劣解集。

3.3 交又操作

交叉方法采用整數交叉法，個體與極值粒子兩兩交叉搜索得到新個體。具體方法是首先隨機選取兩個整數作為交叉位置，假設選取的交叉位置為1和4，個體編碼為[35712658]，極值粒子編碼為[41526783]，然后用極值粒子交叉位置中間的整數替換個體交叉位置中間的整數，其他位置保持不變，得到新個體編碼為[41522658]。產生的新個體若存在相同整數，則用新個體中未出現的整數進行替換，替換后的新個體編碼為[41523678]。最后計算新個體的兩個目標函數值，如果新個體的目標函數值均優于舊個體，則用新個體替換舊個體進行之后的操作。若得到的新個體目標函數值中只有一個目標函數值優于舊個體，則隨機選擇其中一個作為之后操作的粒子個體。

3.4 變異操作

變異方法采用整數替換法，個體自身變異從而得到新個體。具體方法是首先隨機選取兩個整數作為變異位置，假設選取的變異位置為4和6，個體編碼為[35712658]，然后互相交換位置，得到的新個體編碼為[35762158]。最后計算新個體的兩個目標函數值，如果新個體的目標函數值均優于舊個體，則用新個體替換舊個體進行之后的操作。若得到的新個體目標函數值中只有一個目標函數值優于舊個體，則隨機選擇其中一個作為之后操作的粒子個體。

3.5 算法流程

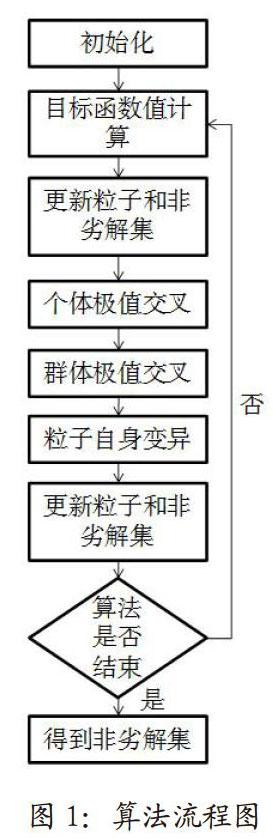
基于混合粒子群算法的多節點協同任務分配流程圖如圖1所示。

其步驟可總結如下：

（1）確定算法的各種初始參數，如算法的初始種群數量，迭代次數等參數;

（2）隨機生成種群中的粒子，產生的粒子為個體編碼序列隨機排列得到。

（3）計算各粒子的兩個目標函數值，兩個目標函數分別為執行任務后目標毀傷價值和代價。

（4）根據目標函數值，更新種群的粒子和非劣解集，并得到種群的個體極值粒子和群體極值粒子。

（5）種群中每個粒子進行交叉、變異操作，若得到的新個體目標函數值均優于舊個體，則用新個體替換舊個體進行之后的操作。若得到的新個體目標函數值中只有一個目標函數值優于舊個體，則隨機選擇其中一個作為之后操作的粒子個體。

（6）更新種群的粒子和非劣解集。當執行步驟5，更新種群的粒子從而進行之后的操作。并更新當前的非劣解集。

（7）判斷算法是否結束。如果未結束，即迭代次數未達到最大，則重復步驟3到步驟6之間的過程。如果迭代次數達到最大，則算法結束，執行步驟8。

（8）得到種群的非劣解集。當算法結束后，得到最終的非劣解集。4仿真計算實例

為驗證所研究的多節點協同任務分配算法的有效性和收斂性，進行仿真計算。在仿真計算中，假設節點數目為4個，目標數目為8個。混合粒子群算法的主要參數設定：初始種群有100個粒子，迭代次數最大為200次，ω₁=0.8，ω₂=0.2。其中節點位置如表2所示。節點對目標的殺傷概率如表3所示。目標自身位置和價值以及節點對目標執行任務后的存活概率如表4所示。

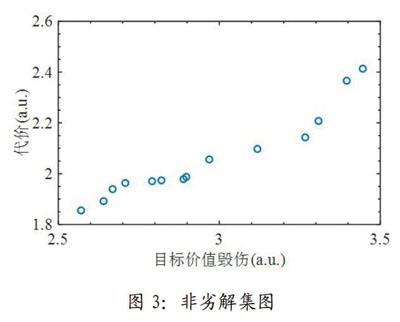
經過200次的仿真計算表明，在上述條件下得到的結果具有穩定性。基于上述條件，首先驗證算法的收斂性。圖2給出了非劣解集中的每代最優的兩個目標函數值隨迭代次數的收斂曲線。在整個算法迭代過程中，兩個目標函數均收斂。其次驗證算法的有效性，多節點任務分配的非劣解集如圖3所示。與單目標優化模型只能得到一個方案相比，本文構建的模型能得到非劣解集，給決策者提供更多信息依據，證明了該算法的有效性。

表5給出了非劣解集中的幾個非劣解中執行任務的目標價值毀傷和代價以及任務集。由表5可知，方案1中，各節點執行任務集分別為（7，8）、（4，1）、（3，5）和（6，2），執行任務后的目標價值毀傷為3.4464，代價為2.4125。方案2中，各節點執行任務集分別為（7，6）、（4，2）、（8，1）和（3，5），執行任務后的目標價值毀傷為2.6695，代價為1.9382。可以看出，按照方案1執行任務后的目標價值毀傷雖然比方案2執行任務后的目標價值毀傷高，但方案1付出的代價同樣比方案2高。因此，在非劣解集中具體選擇哪一個非劣解作為任務分配方案，由進一步需求決定。

5 結束語

針對多節點協同任務分配問題，本文將多節點執行打擊任務的目標價值毀傷和代價作為目標函數，建立多節點協同任務分配模型。利用混合粒子群算法對多節點協同任務分配問題進行求解，得到非劣解集。仿真計算結果驗證了此算法的有效性和收斂性。算法操作相對容易，能快速對問題進行求解。決策者可以根據進一步需求在非劣解集中進行選擇。

參考文獻

[1]龔秀成，蔣曉源，陳華.網絡中心戰體系中的指揮控制[J].火力與指揮控制，2010，35（03）：347-354.

[2]Alberts，D.S.，Garstka，J.J.，Stein，F.P.，Network Centric Warfare：Developing and Leveraging InformationSuperiority[M].Washington，DC：CCRPPublications，Aug 1999.

[3]Andrew S.Tanenbaum，ComputerNetwork[M].Tsinghua UniversityPress，2007.

[4]Rabbath CA，Gagnon E，Lauzon M.On theCooperative Control of MultipleUnmanned Aerial Vehicles[J].IEEECanadian Review，2004（46）：15-19.

[5]姜長生，丁全心，王建剛等.多機協同空戰中的威脅評估與目標分配[J].火力與指揮控制，2008，33（11）：8-12.

[6]Thomas H.Cormen，Charles E.Leiserson，Ronald L.Introductionto Algorithms[M].McGrawHill：MITPress，2001.

[7]葉媛媛，閔春平，朱華勇等.基于整數規劃的多UCAV任務分配問題研究[J].信息與控制，2005，34（05）：548-552.

[8]Goldberg，David E.Genetic Algorithms：Search，Optimization and MachineLearning[M].Boston：Kluwer AcademicPublishers，1989.

[9]Kennedy J.Eberhart R.Particle swarmoptimization[J].IEEE，1995，4：1942-1948.

[10]Curz J B，Jr C，Chen G.Particle SwarmOptimization for Resource Allocationin UAV Cooperative Control [A].AIAAGuidance，Navigation，and ControlConference and Exhibit，Rhode Island，Aug.16-19，2004.

[11]DORIGO M.GAMBARDELLA L M.AntColonies for the TravelingSalesman Problem[J].BioSystems，1997，43（02）：73-81.

[12]戚澤旸，王強，黃英杰.多無人機偵察打擊任務分配建模仿真[J].計算機仿真，2015，32（09）：142-146.

[13]國博，王社偉，陶軍.基于改進粒子群算法的多無人機任務分配研究[J].計算機仿真，2009，26（07）：62-64.

[14]申曉寧，胡維禮.一種多目標優化合作性協同進化算法[J].計算機仿真，2007，24（02）：157-161.

[15]葉秉如，余里紅.多目標二次規劃非劣解集的理論生成及應用[J].水電能源科學，1991，9（02）：102-110.

[16]霍霄華，陳巖，朱華勇等.多UCAV協同控制中的任務分配模型及算法[J].國防科技大學學報，2006，28（03）：83-88.

[17]Dorigo M，Birattari M.AntColony Optimization：a new meta-heuristic[A].in proceedings of theIEEE International Conference onEvolutionary Computation（ICEC99）[C].Piscataway，USA：IEEEPress，1999：1470-1477.

[18]王偉.混合粒子群算法及其優化效率評價[J].中國水運，2007，7（06）：100-101.

[19]汪定偉，王俊偉，王洪峰等.智能優化方法[M].北京：高等教育出版社，2007.