基于指數平滑法的能源綜合安全預測

翟清云 慶亞敏 王默玉

摘要

能源是人民生產生活的物質基礎，是發展社會經濟的重要保證，也是推動我國社會持續、穩定發展的源動力。隨著能源環境約束的進一步強化，能源壓力空前增大，能源需求不斷變化，城市發展導致的能源供需矛盾也愈加突出，因此更需不斷重塑能源安全理念。本文通過層次分析法構建區域能源安全綜合評價，基于指數平滑法對京津冀地區的能源安全進行預測，同時，運用黃金分割法不斷縮小平滑指數區間，最終選取出最合適的平滑指數，提高預測的精度和準確性。

【關鍵詞】層次分析法 指數平滑法 黃金分割法 能源綜合安全

1 引言

20世紀90年代后，我國經濟一直呈現中高速發展狀態，能源需求不斷增大，能源安全問題逐漸顯現，而能源問題與經濟、環境問題緊密相關，由于能源安全問題的不斷突出，導致經濟安全、環境污染問題的加劇。近年來，隨著能源危機的不斷加深，在國家政策的指引下，我國經濟增速逐漸放緩，積極調整以化石能源為主的能源結構，發展新能源新技術，推動科學技術進步，努力實現社會的穩定、可持續發展。京津冀區域作為我國的政治、經濟、文化中心，擁有我國最密集的人口，政府將京津冀一體化協同發展作為一個重大的國家戰略，實現優勢互補、互利共贏。目前我國京津冀區域能源安全總體情況偏弱，該區域能源匱乏，主要能源過度依賴外部運輸，同時由于地理人口條件的限制，能源風險應對能力不足，制約其經濟、環境和社會的可持續發展。以往的能源安全研究主要集中在供應側安全方面，重點研究供應的可靠性、供應的可負擔性以及能源供應風險的應對等問題，而忽略了能源結構、能源環境和能源經濟方面的綜合能源安全研究。隨著近年來，環境友好型社會與低碳經濟的提倡，對能源安全發展提出新的挑戰。研究能源發展現狀，預測中短期的能源安全程度，對于實現經濟、環境和社會的可持續發展具有重要意義。

運用算法對能源安全程度進行預測分析，是制定和實施能源戰略和保障能源發展的重要環節。由于預測的范圍、時間、對象性質等的不同，預測方法也多種多樣，依據預測方法的特點可以將將預測方法分為三類，包括：定性預測法、時間序列分析和因果關系預測。本文選取時間序列中的指數平滑法對京津冀區域能源綜合安全進行預測，該算法是在移動平均法基礎上發展起來的一種時間序列分析預測法，它是通過計算指數平滑值，配合一定的時間序列預測模型對現象進行預測。

2 研究方法

2.1 層次分析法

層次分析法（Analytic Hierarchy Process，簡稱AHP）是一種定性和定量相結合的分析方法，它將復雜的決策系統層次化，通過逐層比較各種關聯因素的組建模型，為分析和決策提供定量依據，具有系統、靈活和簡潔的優點，廣泛應用于政治、經濟、社會等各個領域。層次分析法的主要計算步驟為：

2.1.1 構造層次結構模型

對能源系統進行調查研究，將目標準則體系所包含的因素劃分為不同層次，構建層次結構模型。用不同形式的框圖標明層次的遞階結構和元素的從屬關系，抓住關鍵因素，每一層元素不宜過多。

2.1.2 構造判斷矩陣

按照層次結構，從上到下構造判斷矩陣，本節采用1～9標度方法構造兩兩判斷矩陣。

2.1.3 層次單排序及其一致性檢驗

求解判斷矩陣最大特征值所對應的特征向量。對層次單排序進行一致性檢驗，修正不合格的判斷矩陣。

2.1.4 層次總排序及其一致性檢驗

層次總排序是從上到下逐層進行的。設相鄰兩層次中，層次A包含m個元素A1、A2、…、Am，層次B包含n個元素B1、B2、…、Bn。上一層元素A總排序權重分別為Wj，下一層次元素B關于上一層次元素A的層次單排序權重向量為（p_1j，p_wj，…，p_nj）^T，層次B的總排序權重值為：

2.2 指數平滑法

指數平滑法是一種基于時間序列的預測分析方法，結合了全期平均法和移動平均法的優點，通常用于中短期生產趨勢的預測。基于時間序列的數據往往可以提取相似的特征與規則，而指數平滑法認為最近的數據態勢可以延續到最近的未來，因此對過去的數據給予逐漸減弱的影響程度，即隨著數據距現在的時間長度的增加，賦予的權數逐漸收斂。而二次指數平滑法是對指數平滑值再次計算的方法，其適應性強、結果準確，同時對于非平穩時間序列的預測也十分有用，不僅考慮了時間序列上的線性增長因素，也考慮了二次拋物線的增長因素。二次指數平滑法的計算步驟可以分為以下四個步驟：

（1）計算t時期的單指數平滑值S_t（1），雙指數平滑值S_t（2）、三重指數平滑值S_t（3）

（2）計算t時期的水平A_t、線性增量B_t及拋物線增量C_t

（3）預測m時期以后，即（t+m）時期的數值F_t+m數且m³1

（4）二次曲線指數平滑法的初始值依賴于兩個時期的觀測值x₁和x₂。已知x₁和x₂，假設：S₁^（1）=S₁^（2）=S₁^（3）=x1那么：

其中，α為平滑常數，1吵α0。

從表1可以看出，α取值不同，隨著指數的增加，權數也不斷的變化。當α接近1時，這一情況較為明顯，此時，預測值包括對前一期預測誤差的全部修正值;當α接近0時，新的預測值只包括很小的一部分修正值。一般來說，平滑常數α取的比較大時，預測值F_t+1能夠比較快地反映出時間序列實際的變化情況;當平滑常數α取的比較小時，預測值F_t+1對時間序列的變化反映比較慢，但比較平穩。

因此，平滑常數采用最小均方差的原則進行選取，先選取一組恰當的α值，分別計算其均方差，從中找出使均方差最小的α值，此時的平滑常數為最佳。

2.3 黃金分割法

在選取α值的時候，存在一定的人為因素，導致α在選取的時候具有不確定性，所以為了達到預測的準確與精度，在本章節中采用一種新的α選取方法一黃金分割法，通過實例證明，該方法在一定程度上提高了預測的精度與準確性。黃金分割平滑指數選取步驟如下：

（1）選取[0，1]區間上的黃金分割點作為平滑常數，即α₁=0.618及α₂=0.382，將這兩個平滑常數分別帶入二次曲線平滑法中，進行預測，分別計算不同平滑常數下所對應的均差S，和S₂。若是S₁2，說明α₁比α₂更優的平滑常數，故較優的平滑常數應處于[0.382，1]上。

（2）選取[0.382，1]上的黃金分割點作為平滑常數，即取α₁=0.618及α₃-0.764。按照步驟1中可計算對應α₃=0.764的標準誤差S₃，若是S₃1，故較優的平滑常數應處于[0.682，1]上。

（3）重復上述步驟，可得出較優的平滑常數所在的區間。

（4）當某一區間上的平滑常數對應的標準誤差變化非常小的時候，可以認為此時的平滑常數較為精確了，或者兩者的標準誤差是相等的。此時該區間的中點作為較優的平滑常數。

3 實證分析

3.1 京津冀區域能源綜合安全預測

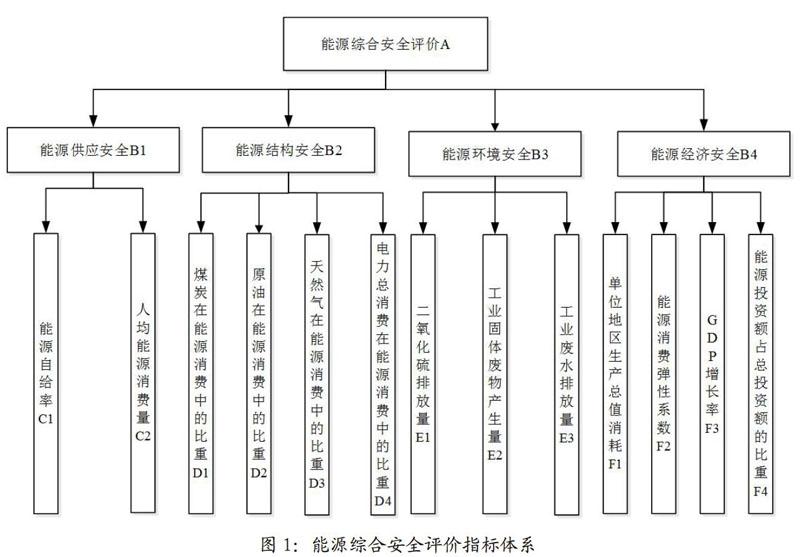
根據層次分析方法建立能源綜合安全評價A指標體系，如圖1所示，根據層次總排序的原則，得出各層次的得分計算公式：

能源供應安全計算公式：

B1=0.586？C1 0.414？C2

能源結構評價計算公式：

B2=0.141，D1 0.141，D2 0.263，D3 0.455，D4

能源環境安全計算公式：

B3=0.6，E1 0.2？E2 0.2？E3

能源經濟安全計算公式：

E4=0.3094？F1 0.1335，F2 0.5030，F3 0.0586？F4

城市能源安全計算公式：

A=0.424？B1 0.122？B2 0.227，B3 0.227？B4

以北京市為例，計算出其在2009年到2015年的能源綜合安全得分，如表2所示。

通過黃金分割法計算得到，當平滑常數取值為α₅=0.326時，其對應的S52=0.8247，當平滑常數取值為α₆=0.292所對應的S62=0.8201.可以看出，α₅和α₆計算的平方差精確到小數點三位，此時可以認為這兩個平滑常數已經相互接近，其誤差可以忽略不計。所以最終的平滑常數取α₅與α₆的中間值作為最優的平滑常數，該最優平滑常數為α=（α₅+α₆）/2。

將選取的最優平滑系數帶入到二次指數平滑法的公式中進行計算，預測出2016年到2020年的北京能源安全綜合得分，同理可以計算出天津、河北以及京津冀地區的能源安全綜合得分，如表3所示。

3.2 結果分析

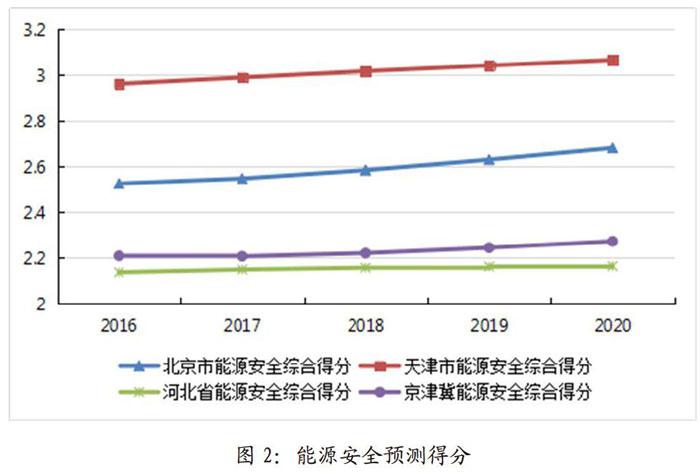
京津冀區域能源綜合安全預測得分趨勢發展如圖2所示。在對于能源綜合安全的預測分析中，通常將能源綜合安全進行等級劃分。設能源安全的總得分為4分，則整個能源安全得分的區間在[0，4]上。由此設立相對應的評價等級如表4所示。

可以看出，在2016年到2020年北京、天津、河北以及京津冀地區能源綜合安全的整體趨勢發展是上升的。其中北京的能源安全上升趨勢比較大，其次天津、河北地區的能源安全增長趨勢比較緩慢。京津冀地區的能源安全得分整體趨勢先下降后增長，但是整體的能源安全得分沒有太大的變化，在預測的這5年中，整體的能源安全得分沒有太大漲幅。通過對比四條曲線可以得出能源安全的綜合排名，天津能源綜合安全得分>北京能源綜合安全得分>京津冀能源綜合安全得分>河北能源綜合安全得分。

4 結論

從以上對京津冀地區能源綜合安全分析預測中，可以得出，京津冀地區的整體能源安全發展處于“一般”等級，整體水平不高，需要進行調整，使得整個京津冀地區能源安全得到提升。從能源綜合安全的角度來看，河北是導致京津冀地區能源安全得分較低一個因素。綜合北京、天津以及河北地區在能源安全各個因素所存在的問題，可以提出相應的對策和建議，來提高京津冀整體的能源安全水平。

4.1 傳統用能企業轉型，優化產業結構

現如今，煤炭、石油的消費比重在京津冀地區占有很高的比重，給能源及環境都帶來了巨大壓力。傳統用能企業轉型，優化產業結構，一方面可以降低化石能源的使用，增加清潔能源的使用;另一方面可以促進新的能源技術的發展，提高能源利用率。尤其是以河北這種工業大省為代表，三個地區之間加強合作，整合能源企業，健全產業鏈，加大技術創新投入，增強區域能源產業的持續創新能力。

4.2 提高新能源開發利用率，優化能源結構

近年來我國加大了新能源的研發和利用，尤其是以風能、水能等可再生能源為主，投入大量的資金與人力突破新的技術瓶頸。鼓勵建設能源互聯網，充分利用各種能源形式轉化為電能，加快能源的流轉速度，實現清潔替代、電能替代，完成新一輪能源建設的迭代發展。

4.3 優化京津冀地區政府合作機制，協調各個地區的發展

京津冀地區的經濟發展極不平衡，平衡三個地區的能源發展，需要各地區的政府相互協調，對能源建設做出統一的規定，并監督實施，保證能源產業鏈條的完整，消除三個地區能源發展的壁壘，提高整個京津冀地區能源綜合安全。

參考文獻

[1]F.Lin，L.Zhang，H.Xu and Y.Sun，"AnImproved Exponential SmoothingModel on Rental Trends Predictionof Public Bicycle Stations，"2016IEEE 14th Intl Conf on Dependable，Autonomic and Secure Computing，14thInt1 Conf on Pervasive Intelligenceand Computing，2nd Intl Conf on BigData Intelligence and Computingand Cyber Science and TechnologyCongress（DASC/Picom/DataCom/CyberSciTech），Auckland，New Zealand，2016，pp.437-441.

[2]D.Nadyatama，Q.Aini and M.C.Utami，"Analysis of commodityinventory with exponential smoothingand silver meal algorithm（Casestudy），"2016 4th InternationalConference on Cyber and IT ServiceManagement，Bandung，2016，pp.1-6.

[3]R.Anggrainingsih，G.R.Aprianto andS.W.Sihwi，"Time series forecastingusing exponential smoothing topredict the number of website visitorof Sebelas Maret University，"20152nd International Conference onInformation Technology，Computer，andElectrical Engineering（ICITACEE），Semarang，2015，pp.14-19.

[4]R.Con Ion，J.Dumazert，V.Kondrasovs，E.Roh e e and S.Normand，"Estimationof Nuclear Counting by a NonlinearFilter Based on a Hypothesis Test anda Double Exponential Smoothing，"inIEEE Transactions on Nuclear Science，vol.63，no.5，pp.2671-2676，Oct.2016.

[5]方形.區間層次分析法（IAHP）在財務決策中的應用[J].山東輕工業學院學報（自然科學版），2006（04）：91-95.

[6]劉璐.北京市能源安全預測與情景分析[D].華北電力大學，2012.

[7]王歡.“呼包銀印”經濟區能源安全評價及預警系統構建研究[D].內蒙古科技大學，2015.

[8]鄔春明，林歡.基于二次曲線指數平滑法的風電桿塔預警模型研究[J].電力系統保護與控制，2014，09：81-85.

[9]何俊，劉林兵，唐一舉.基于線性二次指數平滑法的瓦斯含量預測[J].煤炭科學技術，2014，12：48-50+61.

[10]王慈光.二次指數平滑法中確定初始值的簡便方法[J].西南：交通大學學報，2004，03：269-271.