落角約束最優制導律在空地導彈上的應用*

陳 韻,常 燕,苗昊春,嚴憲軍

(1 西北工業大學航天學院,西安 710072;2 火箭軍工程大學,西安 710025;3 西安現代控制技術研究所,西安 710065)

0 引言

隨著武器作戰樣式的變革,在精確打擊運動裝甲目標的武器系統設計中,除了命中精度這項基本要求外,還需要在命中時刻具有一定的命中角度,以提高戰斗部的毀傷效能。近年來具有終端角度約束的制導方法受到越來越廣泛的關注,國內外學者進行了很多相關研究,根據理論基礎的不同,具有終端角度約束的制導律主要有過重力補償比例導引律,變結構制導律,最優制導律以及其他類型的制導律[1-7]。過重力補償比例制導律[2]原理簡單,易于工程實現,但只能用于增大落角,不適用于小落角的情況,且對于落角期望值>30°的情況也不能很好適應。采用變結構理論[3]的帶落角約束制導律也有較多的研究,對機動目標具有較好的魯棒性,但是變結構控制容易存在振顫問題。

目前直升機載空地導彈通常配裝有多種戰斗部。配裝破甲戰斗部時,采用大角度頂攻方式可以對地面裝甲目標進行有效毀傷;但對于堅固的工事目標,攻堅戰斗部又對制導系統提出了小角度平射攻擊方式的要求。文中利用最優控制理論研究帶有落角約束的制導律,通過設置不同的期望落角值,實現一套制導控制系統適應多種落角的需求。

1 相對運動建模與分析

導彈接近目標過程中與目標的相對幾何關系見圖1。圖中:Oxy為導彈運動縱向平面;M為導彈,在發射坐標系中的坐標為(xm,ym);V為導彈速度,速度方向與水平面夾角θ即彈道傾角,速度方向與彈目線夾角η;T為目標,在發射坐標系中的坐標為(xt,yt);q為彈目視線角。

根據導彈目標角度和幾何相對關系,可以得到相對運動方程[8]:

(1)

為保證導彈能精確命中目標,必須設計合適的制導律來控制導彈的飛行路徑。制導律是指作用于導彈的法向加速度ac與彈目相對運動狀態的關系,其中:

(2)

2 最優制導律

基于最優控制原理推導帶落角約束的制導律。

對式(1)中的第二項進行微分可以得到:

(3)

建立狀態方程

(4)

其中:

θf為彈道終端落角期望值。

對于各狀態變量,起始時刻有:

終端條件為:

x1(tf)=0x2(tf)=0

考慮到終端約束,選擇如下二次型性能指標:

(5)

式中:

為加權矩陣,此處F→∞。由最優控制理論可知,最優控制解為:

(6)

式中:R=1,

P為滿足以下Riccati方程的解:

(7)

令:

則式(7)可以表示為:

(8)

因q12=q21,則有:

(9)

由式(9)中第三式可得:

(10)

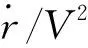
(11)

將式(11)代入式(9)的第二式,則有:

(12)

將自變量t變為r,可得:

(13)

當t=tf時,q22(tf)=0,r(tf)=0,近似認為V為常值,則有:

(14)

(15)

從而可求解得到逆矩陣P-1:

(16)

則:

(17)

代入式(6)得到最優控制:

(18)

即:

(19)

根據式(2)可以得到具有角速度反饋形式的最優制導律表示為:

(20)

從式(20)中可以看出,最優制導律中的第一部分與傳統的比例導引制導律一致,與視線角速度成比例關系,確保導彈命中目標;增加的第二項即是角度約束項,以保證命中點處的速度方向滿足要求。

3 仿真驗證

3.1 仿真條件

落角約束最優制導律仿真驗證原理框圖見圖2所示。

以某直升機載空地導彈為例進行落角約束制導律的仿真驗證。設導彈初始發射高度為300 m,導彈飛行速度約為200 m/s,目標距離為5 000 m,采用發射前鎖定攻擊模式。建立六自由度彈體運動模型,對最優制導律進行仿真驗證。

從章節2的推導分析可知,只要設置期望落角值θf,利用式(20)的最優制導律可以實現導彈以彈道傾角θ(tf)=θf,精確命中目標。

3.2 仿真結果

分別設置期望落角值θf值為0°、-15°、-30°、-45°。落角、脫靶量仿真結果見表1,仿真曲線見圖3～圖5。

期望落值/(°)實際值/(°)脫靶量/m0.00.2930.056-15.0-14.960.022-30.0-29.950.034-45.0-44.480.083

從圖3可以看出,期望的落角絕對值越大,彈道需要爬升的高度越高;從圖4可以看出導彈命中時刻的傾角與期望值基本一致;從圖5可以看出飛行過程的需用過載在-2g～+4g范圍內,滿足導彈可用過載能力;從圖6可以看出,導引頭框架角在-25°～+10°范圍內,滿足導引頭技術指標。

4 結論

目前直升機載空地導彈對末端落角提出了多種要求,文中研究的是一種最優制導律,在滿足精度的前提下,可實現導彈能力范圍內對目標的任意落角攻擊。經仿真分析表明:

1)該制導律基于最優控制理論推導得到,由兩部分組成,第一部分與比例導引一致,滿足命中精度,第二部分與彈目相對關系及期望落角相關,實現落角約束。

2)該制導律通過對彈道的抬高來實現對落角的增大,且需用過載及導引頭框架角均滿足要求。

3)該制導律實現的需用信息均可在彈上通過制導部件獲取,公式簡單,易于工程實現。