曲線小波光順問題中關于連續分辨率水平的研究

陳 勇 張 旭 吳易澤 江明陽

（上海工程技術大學機械與汽車工程學院，上海 201620）

由于制造精度和測量精度不能達到理想狀態，會造成零件產生一定數量誤差，對曲線或者是曲面光順性產生不利影響。光順技術可以減少制造精度和測量精度對逆向工程產生的影響，進而保證逆向工程下產品質量。逆向工程中，多分辨分析技術是一種提取曲線曲面本質特性的方法，其不僅具有良好的時域局部特性，還具有良好的頻域局部特性。S.Mallat在1998年構造正交小波基時，提出了多分辨分析這個概念，從空間概念上說明了小波具有多分辨率特性，將此之前的所有關于正交小波基構造進行了統一，并提出了正交小波基構造方法和正交小波快速算法，這個算法就叫做Mallat算法[1]。

1994年，Quak等研究人員利用多分辨分析方法，對由2j+3個控制頂點確定的一條曲線，提出了基于閉區間的B樣條小波曲線分解和重構算法[2]。在多分辨光順問題研究中，國內外許多學者做了研究，比如紀小剛等人在二進小波基礎上，實現了曲線或者是曲面小波光順任意定點的控制[3]；再例如趙罡等研究人員提出了一種基于小波的非均勻B樣條曲線自動光順算法，將曲線分解為曲線細節部分和曲線尺度兩部分，并把細節部分再次分解為小波尺度部分和小波細節部分，最后通過自動設定閾值對小波細節部分進行修復[4]。

本文主要介紹連續分辨率水平的建立及其相對于以往多分辨率水平方法的優勢，并基于非均勻B樣條光順問題構造建多分辨水平基函數，通過這個基函數達到曲線光順連續控制目的，這樣曲線調整方法相對于傳統方法更加容易達到曲線光順要求，是解決曲線設計中關于光順性問題的一種有效思路。

1 關于建立連續分辨率水平的基本知識

相關研究者提出了關于相鄰兩個整數分辨率水平曲線進行線性插值，最終得到過渡曲線的方法，如式（1）所示。

式中，Ψ（t，x）表示一條曲線；x為分辨率水平；t為節點矢量；γn（t）為非均勻B樣條曲線；n為節點矢量；μ為過渡系數，0≤μ≤1。

由上述方程中，可得曲線對x連續，并且定義：Ψk（t，x）（k=1，2， ……）表示一條曲線；x為其分辨率水平。如果Ψk（t，x）對x是k有階的偏導數，同時Ψk（t，j）=γj（t），則x稱為k階連續分辨率水平，一般情況下k值取1或者2。

2 構造連續分辨率水平

2.1 設計連續分辨率水平基函數

根據連續分辨率水平以及非均勻B樣條小波變換知識，一般情況下假設k取1或者2，并構造符合如下條件的基函數g1（x）、g2（x）。g1（x）、g2（x）是關于 y軸對稱的，符合插值函數要求。另外，對于任意的x都有g1（x）≥0、g2（x）≥0，且滿足一定條件，如式（2）所示。

式中，k取值為1或者2，可得曲線插值關于基的和為1，其支撐區間在[-1，1]上是連續變化的并且具有k階連續導數；在[-1，1]外的值都為零，這就保證了其支撐區間是[-1，1]，更方便處理邊界位置，適用于整數點插值。另外，當gk（0）=0、gk（i）=0時，整數點N處的曲線為γn（t），為非均勻B樣條曲線。

綜上所述，插值函數如式（3）所示。

式中，k為連續分辨率水平構造基函數序號；J為控制點層數；Ψk（t，x）為分辨率水平x有k階連續導數。由于g1（x）、g2（x）的性質，在區間[N，N+1]上，可以通過第N層曲線和第N+1層曲線來構造關于連續分辨率水平x的曲線，如式（4）所示。

有小波變換可得式（5）。

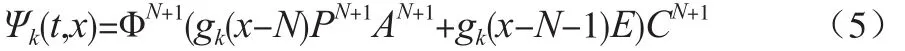
式中,ΦN+1為非均勻B樣條基函數；PN+1為小波尺度重構矩陣；CN+1——非均勻B樣條曲線原控制點；E為單位矩陣；AN+1小波分解矩陣，Ckx如式6所示。

則可得Ψk（t，x）連續導數，如式（7）所示。

式中，ΦN+1為非均勻B樣條基函數；Ckx為經過小波變換以及連續分辨率水平構造修改后的控制點。從上述公式中可以看出，Ckx是分辨率水平為x的曲線Ψk（t，j）的控制點，分辨率水平x的連續變化決定了控制點連續變化，而控制點的連續變化決定了分辨曲線也是連續變化的，這樣就可在誤差允許范圍內找到符合要求的曲線。

2.2 算法步驟

非均勻B樣條曲線小波光順中關于連續分辨率水平建立的步驟如下：

（1）選取控制點構造非均勻B樣條曲線，控制點數量是2j+3個。節點矢量是依據控制點數據按照Hartley-Judd方法生成。

（2）構造兩種插值核函數g1（x）、g2（x），構造要求如第一部分所述。

（3）構造插值函數如式（1）所示。

（4）按照式（7）所示來計算出最終所需求曲線。

2.3 實例分析

選取一個由131個控制點組成的非均勻B樣條曲線，按照上述方法對曲線進行光順處理，試驗驗證流程如圖1所示。利用MATLAB軟件對算法進行驗證，這只需要調整分辨率水平x值就可以實現對曲線的連續控制，并且隨著連續分辨率水平x值的變化，曲線的效果也是不同，可以根據各行業要求選擇合適的連續分辨率水平x。

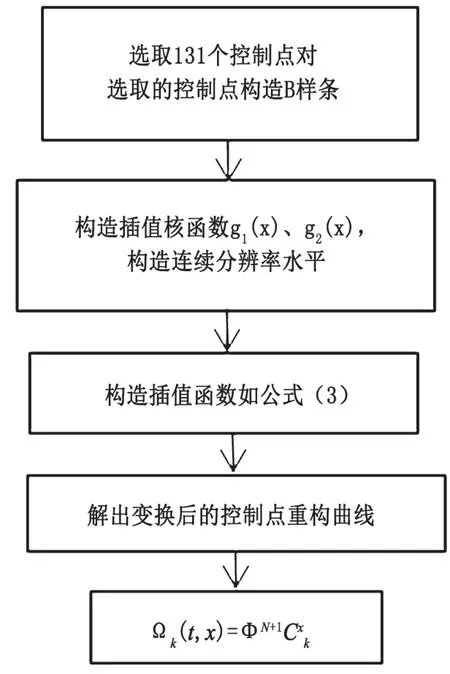
圖1 連續分辨水平驗證流程圖

從流程圖上可以看出，連續分辨率水平建立就是運用具有特征性的連續插值核函數來實現的。設置一個連續分辨率水平x=3.7，在N≤x≤N+1情況下，對構造曲線進行分析，當x取值不同時，構造曲線會有不同效果，這樣就有更大的分辨率水平區間來保持曲線細節部分。選取的構造函數如圖2所示。

按照Hartley-Judd方法獲得非均勻B樣條曲線，如圖3所示，為了使非均勻B樣條曲線得到最好的光順效果，并且在需要時保留曲線細節，可以選擇不同分辨率水平再求得最后光順。

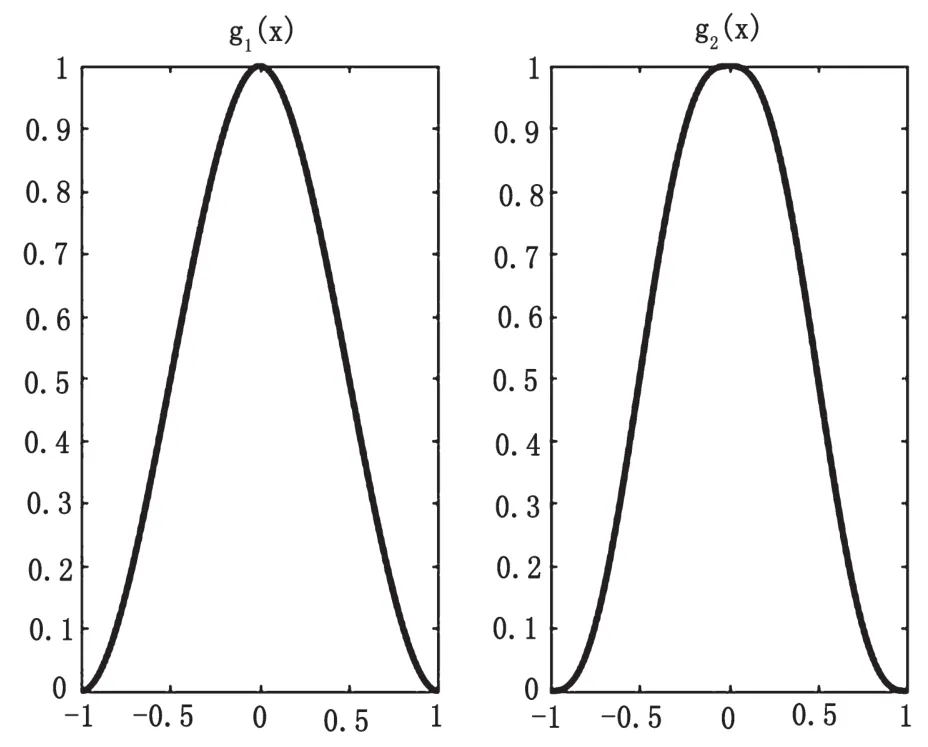
圖2 連續分辨率水平構造函數

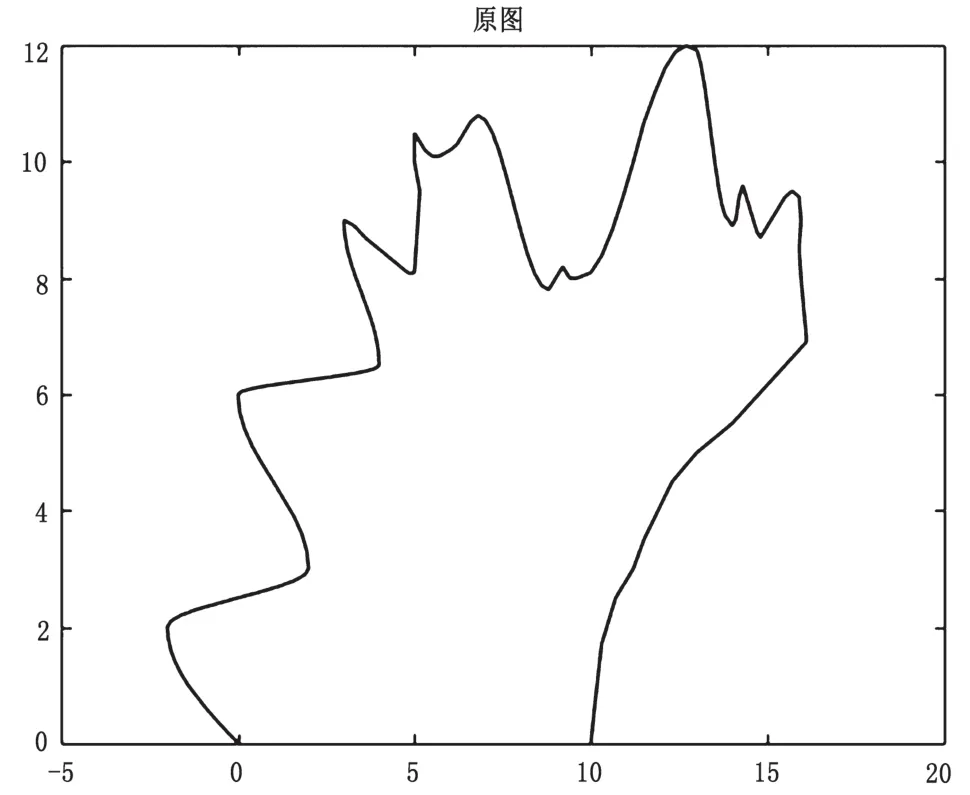
圖3 非均勻B樣條曲線

兩曲線對比圖如圖4所示，局部放大圖如圖5所示，和原曲線相比，非均勻B樣條曲線可以有更好光順性，并且隨著分辨率的連續構造，總能獲得需要的非均勻B樣條光順曲線。

圖4 曲線對比圖

圖5 曲線局部放大

本實驗驗證了非均勻B樣條曲線光順過程中仍然能構造連續分辨率水平，達到最終的光順目的。在實驗過程中，數據點選擇和非均勻B樣條曲線選擇，構造出具有不同分辨率的曲線，能夠實現不同行業要求，對于光順性要求比較高而對擬合曲線精度要求不是太嚴格的行業，可以在同層次下選擇比較小的分表率水平，能達到更好的光順效果。

3 結論

本文主要介紹了曲線小波光順性問題中關于連續分辨率水平的構造問題，在小波變換中結合連續分辨率水平可以達到曲線連續控制目的，在一定誤差允許范圍內得到符合本行業要求的光順曲線。經驗證，本文構造的連續分辨率水平對非均勻B樣條曲線進行小波光順過程是有效的，并且在一定范圍內可以帶給工程人員更多的光順性調整方案，使其在光順性和逼近精度之間有一個更好的選擇。