基于擴展卡爾曼濾波的多旋翼飛行器融合姿態解算算法

丁 磊，吳蔚劼，方 挺

(1.安徽工業大學電氣與信息工程學院，安徽馬鞍山243000；2.西安電子科技大學通信工程學院，陜西西安710126)

多旋翼飛行器是一種能夠自由起降，且能穩定懸停于空中的六自由度飛行器。該飛行器起飛不受場地限制，可在任意場合下工作，甚至可用于執行各種高危任務，故其在偵察敵情、災區救援、道路監控、農業植保、電力巡線等領域有較好的應用前景[1]。姿態控制是飛行器總體設計的重要組成部分，而姿態解算是飛行控制系統的核心。飛行器具有欠驅動、多變量等比較復雜的特性[2]，其穩定飛行與靈活控制對實時姿態解算的要求更高[3]，故飛行器姿態角的實時解算算法是多旋翼飛行器研究的熱點之一。

利用慣性導航測量器件如加速度計、陀螺儀和電子羅盤可快速、穩定地測量飛行器的當前姿態角，但多旋翼飛行器飛行時電機高速轉動，機身隨之產生高頻振動，加速度計對機身振動異常敏感，致使其測量數據中摻雜大量高頻噪聲，導致后續姿態解算的結果產生較大誤差。常用飛行器飛行姿態的解算算法有歐拉角、方向余弦、四元數互補濾波算法等。其中：歐拉角法解析過程比較簡單，但包含大量的三角函數運算，計算時間較長，且當俯仰角轉動90°時會出現萬向鎖現象，不能進行全姿態解算[4]；方向余弦法可避免萬向鎖現象的發生，能夠進行全姿態的解算，但姿態矩陣微分方程是線性微分方程并含9個未知量，計算量大，實時性較差[5]；四元數法僅含4個未知量，計算量小且算法易編程實現，可進行全姿態的解算[6]；互補濾波算法是一種數據融合算法，其根據傳感器的不同特性，通過融合低通濾波和高通濾波接近真實信號[7]。徑向基(radial basis function，RBF)神經網絡是一種局部逼近網絡，具全局唯一最佳逼近的特性，且其結構簡單、訓練速度快[8-9]。鑒于此，以四元數互補濾波算法解算的多旋翼飛行器姿態角作為參考向量，采用RBF神經網絡設計加速度計非線性高頻濾波器，用擴展卡爾曼濾波算法實時解算飛行器的姿態角，以期抑制機身振動對加速度噪聲的干擾，提高飛行器姿態角的解算精度。

1 姿態解算

1.1 慣性導航

假設飛行器坐標系為Hb，大地坐標系為Hc，將飛行器坐標系分解成按Z-Y-X軸順序轉動，3次轉動均繞飛行器坐標系的某一軸。首先飛行器繞大地坐標系Z軸，以右手系轉動角度ψ得到飛行器新的坐標系，ψ為飛行器的偏航角Yaw。繞Z軸定軸轉動的基本旋轉矩陣為

再繞新的機體坐標系Y軸，以右手系轉動角度θ，得到飛行器新的坐標系。θ為飛行器的俯仰角Pitch，繞Y軸定軸轉動的基本旋轉矩陣為

最后繞新的機體坐標系X軸，以右手系轉動角度φ，得到飛行器的最終坐標系。φ為飛行器的橫滾角Roll，繞X軸定軸轉動的基本旋轉矩陣為

3次分解的動作可視為飛行器從初始位置到最終位置的一次性等效旋轉。按歐拉角Z-Y-X依次進行轉動，令旋轉矩陣為，則

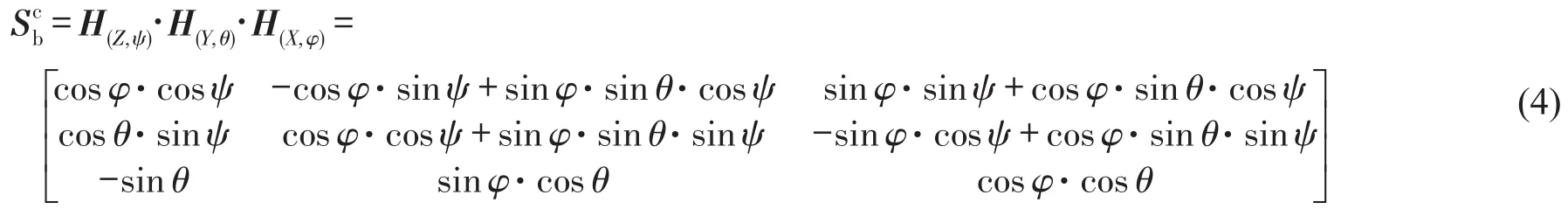
由式(4)旋轉矩陣可直接解算出飛行器的偏航角ψ、俯仰角θ和橫滾角φ，如

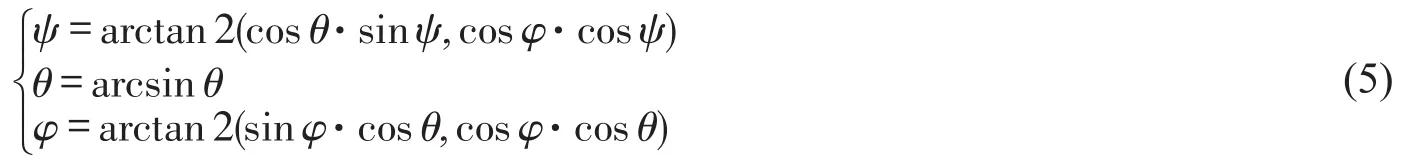
1.2 四元數互補濾波算法

1.2.1 姿態角的四元數法表示

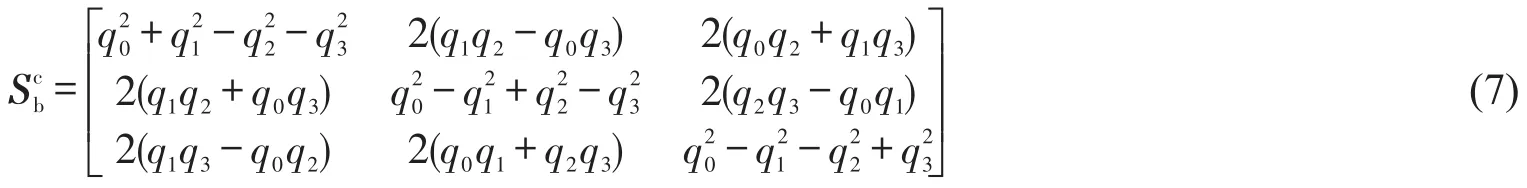
從式(7)可獲得飛行器的偏航角ψ、俯仰角θ和橫滾角φ。

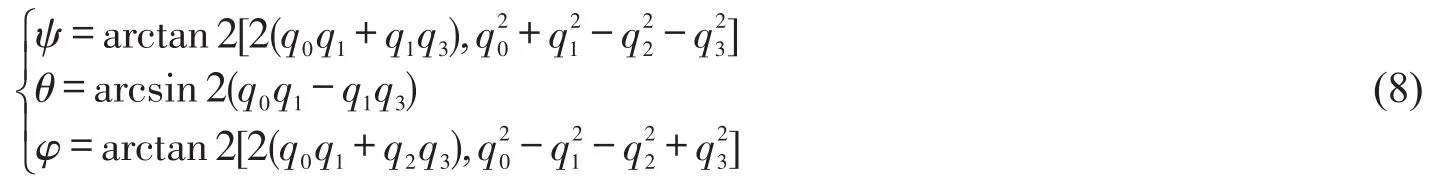
1.2.2 互補濾波算法

對于6軸運動處理組件MPU6050，加速度計對多旋翼飛行器的加速度較為敏感，用加速度計的實時值計算飛行器當前傾角誤差較大；陀螺儀經過積分得到的角度不受加速度計的影響，但隨時間的推移，其積分漂移和溫漂會引起較大誤差[11-13]。

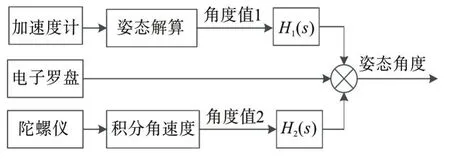
圖1 互補濾波原理Fig.1 Principle of complementary filter

根據互補濾波的工作原理(如圖1)，假設加速度計的測量數據為t1=r+e+u1，陀螺儀的測量數據為t2=r+e+u2，其中r為真實數據；e為傳感器本身的誤差；u1，u2分別為高頻噪聲和低頻噪聲。設傳遞函數之和為1，為低通濾波器，用來濾除加速度計的高頻噪聲；為高通濾波器，用來濾除陀螺儀的低頻噪聲。通過互補濾波得到估計傳遞函數：

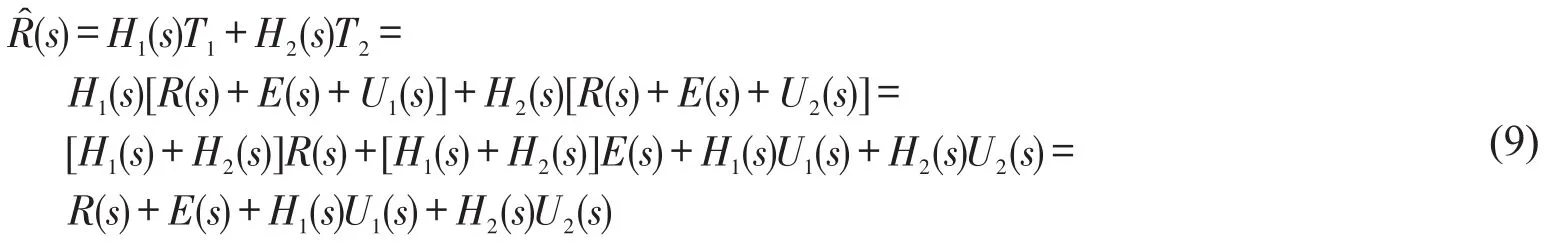
其中：R(s)和E(s)為全通量，包含真實數據和傳感器本身的誤差，而加速度計中所含的高頻噪聲信號U1(s)被H1(s)低通濾波器濾除，只容許低頻信號通過；陀螺儀所含的低頻噪聲信號U2(s)被H2(s)高通濾波器濾除，只容許高頻信號通過。互補濾波算法根據陀螺儀、加速度計的不同特性，短時間內采用陀螺儀的數據作為最優參考，同時對加速度計的數據進行滑動窗口濾波處理，用其得到的值不斷地對陀螺儀的數據進行校正[14-15]，通過融合低通濾波和高通濾波計算出接近真實信號的數據，供后續飛行器姿態解算使用。

2 RBF神經網絡非線性濾波

RBF神經網絡輸入層與隱藏層間的映射為非線性關系，隱藏層與輸出層間的映射為線性關系[16]，其網絡結構如圖2。RBF神經網絡隱藏層神經元的輸出為

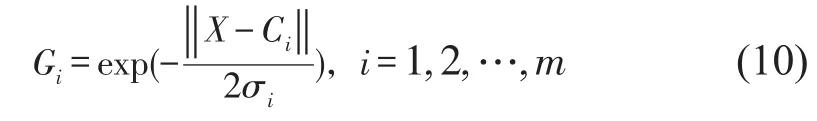
其中：X為含有噪聲的m維加速度計數據，作為輸入向量；Ci為第i個神經元基函數的中心；σi為第i個神經元的基寬；Gi為高斯徑向基函數。

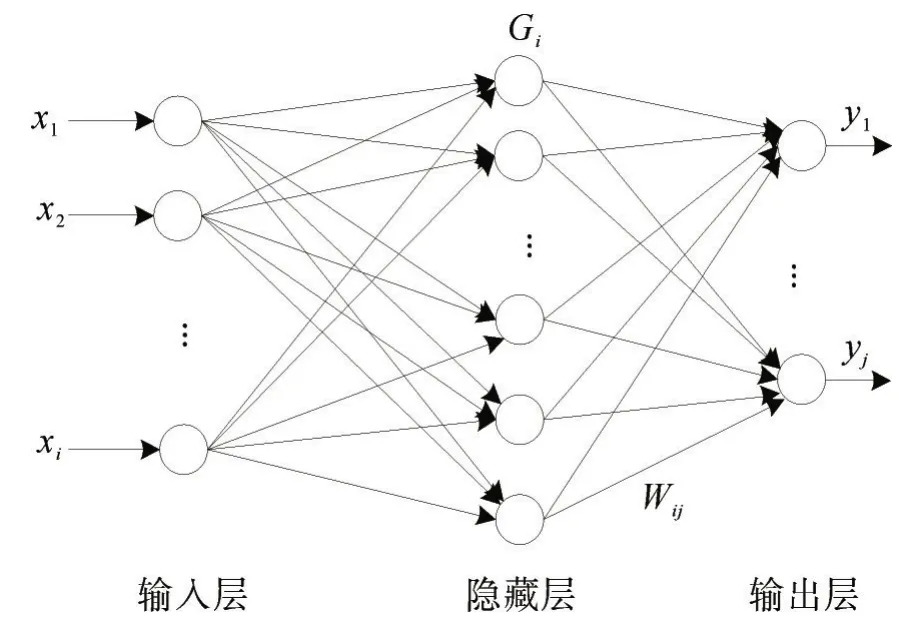
圖2 RBF神經網絡結構Fig.2 Structure of RBF neural network

RBF神經網絡輸出層的輸出yj為

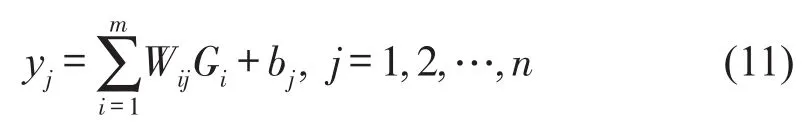
其中：Wij為隱藏層第i個神經元與輸出層第j個神經元間的權重；bj為輸出層第j個神經元的閾值。

RBF神經網絡辨識器的性能評價函數J(k)為

其中：k為任一時刻；yj(k)為實際輸出；為網絡輸出，經過網絡訓練，使得J越小越好，滿足J≤ε的條件，ε為一個極小的正數。

RBF神經網絡中心的選取采用自組織學習法，通過監督學習訓練隱藏層與輸出層間的權值和閾值[17]。網絡的權值經由梯度下降算法計算不斷改變，能夠快速收斂到全局最優點。權值的更新算法為

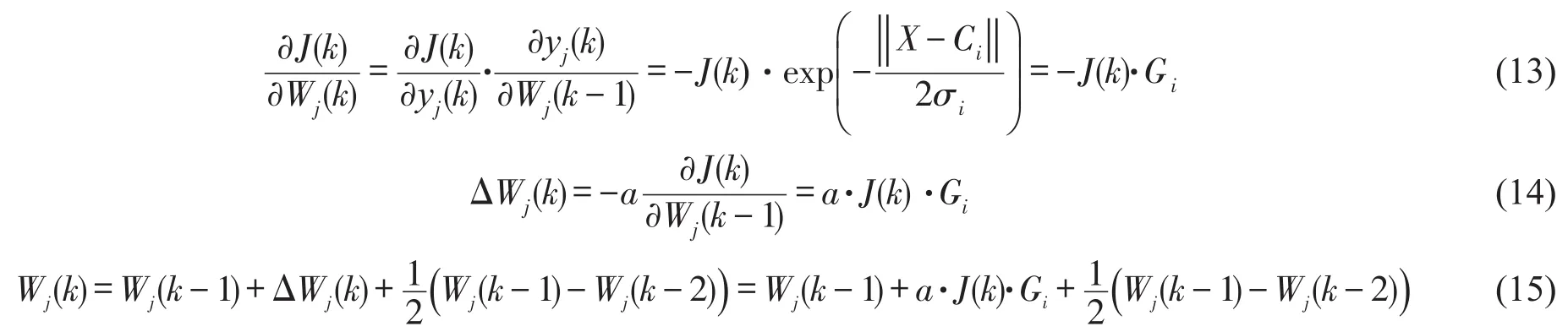
其中a為學習速率，文中取0.1。學習速率太大則無法快速逼近最優值，會在其附近來回振蕩；太小則收斂速度太慢。

非線性濾波器的權值系數含實時性的問題，需能夠實時、快速求解。系統的非線性差分方程可表示為

式中：p為當前時刻，p+1為下一時刻，前者為系統的狀態方程；后者為系統的觀測方程；f，h為非線性函數；v和w為白噪聲序列且均值為0。非線性濾波的最優值是通過y(p)來估計出系統的(p)，并使其是x(p)的最優估計。RBF神經網絡實際上是系統對f和h兩個非線性函數的最佳逼近。

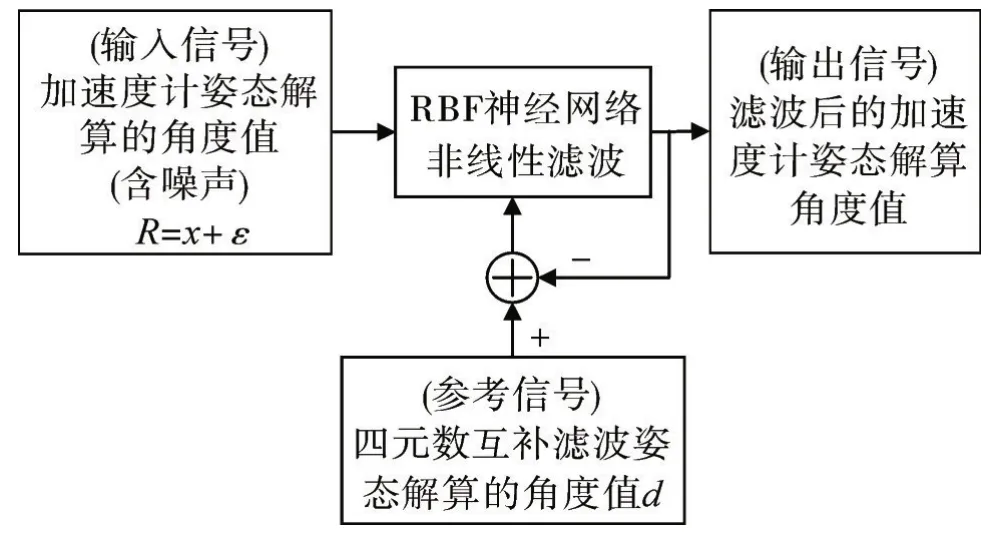
圖3 加速度計RBF神經網絡非線性濾波基本原理Fig.3 Basic principle of nonlinear filtering of accelerometer RBF neural network

利用RBF神經網絡對加速度計姿態解算的角度值進行非線性濾波的基本原理如圖3。圖3中加速度計解算的角度作為輸入信號，該信號包含真值X與噪聲ε，參考信號d為互補濾波姿態解算算法解算出的角度，經RBF神經網絡非線性濾波算法得到輸出信號Y。

3 擴展卡爾曼濾波融合姿態解算算法

多旋翼飛行器系統為非線性系統，傳統的卡爾曼濾波算法只適用于線性系統，故文中采用擴展卡爾曼濾波算法(EKF)解決多旋翼飛行器系統的非線性問題[18-20]。擴展卡爾曼濾波算法將系統的非線性部分進行泰勒級數展開，忽略其高階無窮小部分，同時保留系統的線性部分，最終得到近似模型，將其非線性問題轉化為線性問題[21-23]。其通過上一時刻的角度X(k)預測更新下一時刻的角度X(k-1)，是一種典型的遞推算法，包括系統狀態方程和觀測方程的建立。

建立系統的狀態方程，如

其中W(k-1)為系統的噪聲向量，選取互補濾波姿態解算算法解算出的姿態角為系統的狀態量，誤差較小。

建立系統的觀測方程，如

式中：H為單位矩陣；Vk為觀測的測量噪聲。將經RBF神經網絡非線性濾波后的加速度計解算的角度作為觀測向量。

之后，通過以下步驟完成系統狀態的預測與更新[24-25]。

1)狀態的預測

式中：A為系統參數矩陣；X(k|k-1)為利用上一時刻狀態預測的結果；X(k-1|k-1)為上一時刻的最優預測值；B為控制參數矩陣；U(k)為當前狀態的控制量。通過上一時刻的最優預測值預測下一時刻的狀態值。

2)協方差矩陣的預測

其中P(k|k-1)為X(k|k-1)對應的協方差矩陣，同時也是P(k-1|k-1)協方差矩陣的估計，Q為系統噪聲。

3)卡爾曼增益的更新

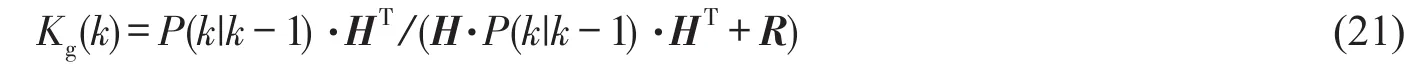
式中：Kg(k)為卡爾曼增益；R為觀測噪聲的協方差矩陣。

4)狀態的更新

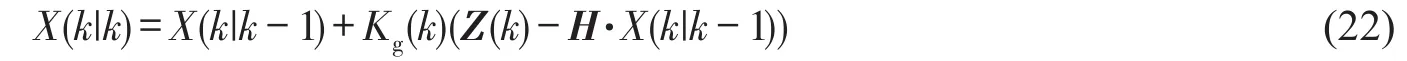
其中Z(k)為觀測矩陣。

5)協方差矩陣的更新

其中E為單位矩陣。

擴展卡爾曼濾波融合姿態解算算法的原理圖如圖4。

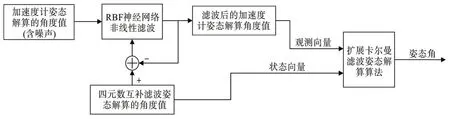
圖4 擴展卡爾曼濾波融合姿態解算算法原理Fig.4 Principle of extended Kalman filter fusion attitude solving algorithm

4 實驗仿真分析

基于STM32單片機、MPU6050六軸運動傳感器及HMC5883電子羅盤，組成飛行器姿態解算硬件系統，利用提出的四元數互補濾波姿態解算算法對飛行器的俯仰角、橫滾角、偏航角分別進行靜態和動態的實時解算。偏航角的解算需用到電子羅盤，利用加速度計只能單獨進行俯仰角及橫滾角靜態和動態兩種情況的解算，之后采用RBF神經網絡對加速度計解算的姿態角進行非線性高頻濾波，其中徑向基函數的擴展系數取1.0。最后通過擴展卡爾曼濾波融合姿態解算算法解算出飛行器靜態和動態的俯仰角和橫滾角。系統每2 ms進行1次姿態角解算。互補濾波姿態算法解算的結果如圖5，6。加速度計姿態角濾波前的結果如圖7。加速度計解算的姿態角經RBF濾波后的結果如圖8。擴展卡爾濾波解算的姿態角靜態動態結果如圖9，10。

從圖5可看出：互補濾波姿態解算算法解算出的靜態姿態角效果良好，俯仰角的解算范圍在(-0.23°，+0.23°)，橫滾角的解算范圍在(-0.2°，+0.27°)，經過水平校準后，可基本保持在0°附近，且在長時間測量過程中角度沒有發散；偏航角的解算幅度在0.5°以內，長時間范圍內穩定、不發散。從圖6可看出，互補濾波姿態解算算法解算出的動態姿態角數據曲線有少許毛刺，但從總體效果來看，姿態角的解算效果實時性強、不發散，姿態跟蹤速度快，能夠滿足基本日常飛行需求。從圖7可看出，加速度計僅通過滑動窗口濾波，因高頻噪聲的干擾導致姿態角波動范圍較大，靜態時的角度波動范圍達到2°，動態時有尖峰產生，波形毛刺較多，測量誤差較大。從圖8可看出：加速度計解算的姿態角經RBF神經網絡非線性高頻濾波，靜態測量的姿態角較為穩定，趨近于0°且高頻噪聲得到有效濾除；姿態角振幅在0.2°左右，動態測量的姿態角與濾波前相比，濾波效果較為明顯，尖峰部分得到一定程度減弱，高頻噪聲得到有效抑制，數據波形更加穩定、光滑。

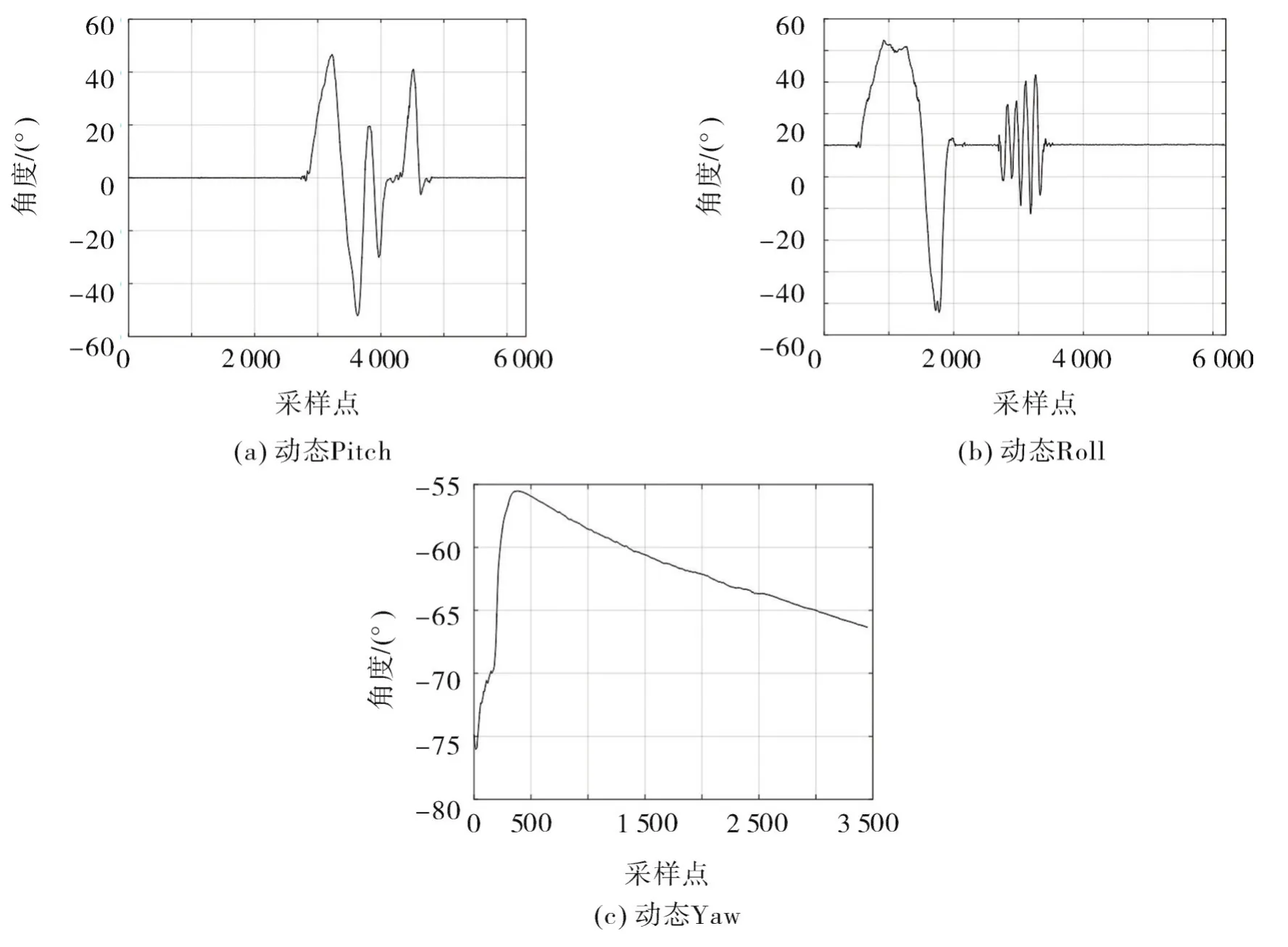
圖6 互補濾波姿態解算動態結果Fig.6 Dynamic results of complementary filtering attitude solution

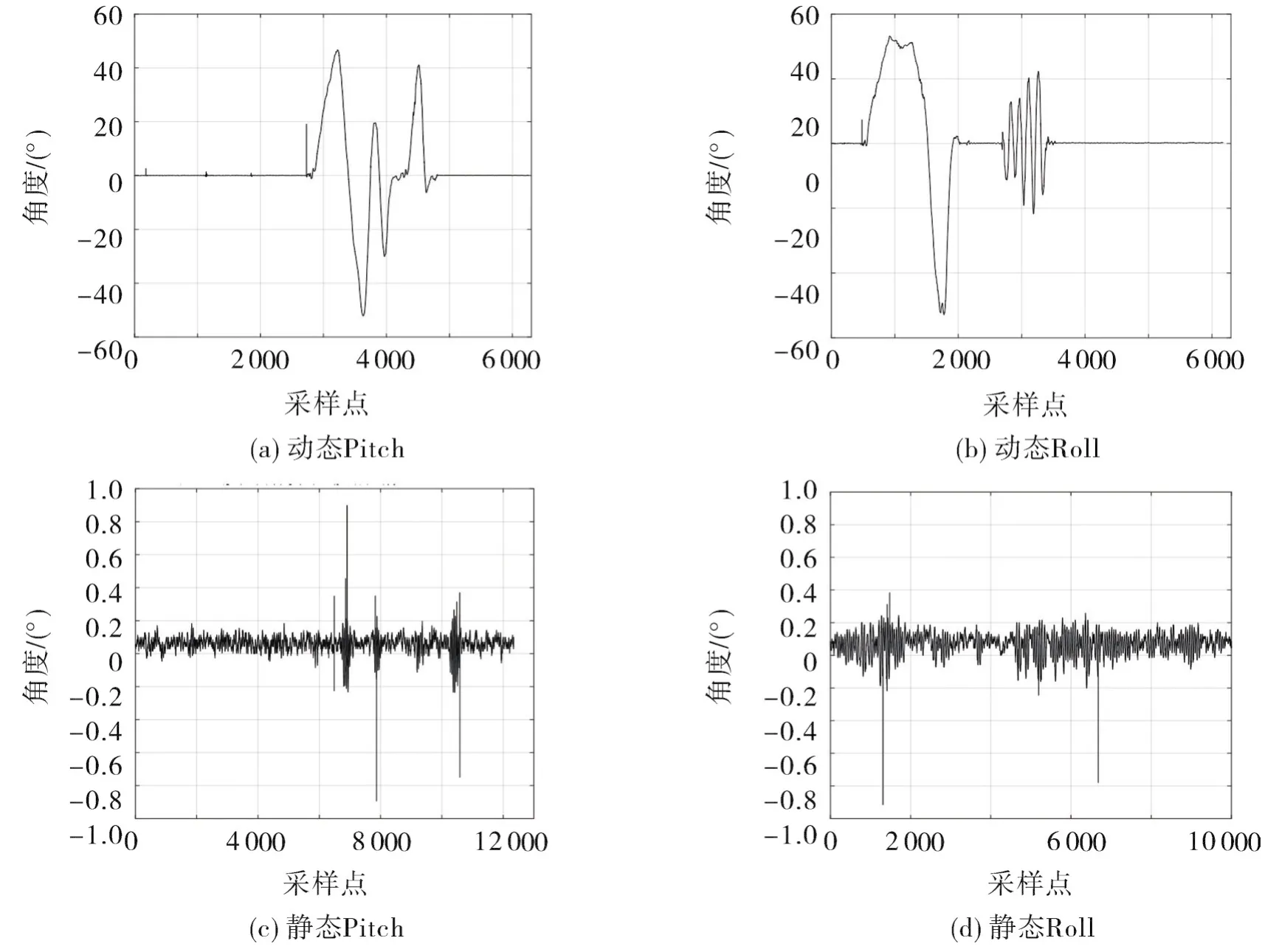
圖7 加速度計姿態解算濾波前的結果Fig.7 Results of accelerometer attitude solution before filtering

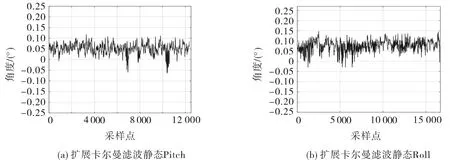
圖9 擴展卡爾曼濾波解算的姿態角靜態結果Fig.9 Static results of the attitude angle calculated by extended Kalman filter

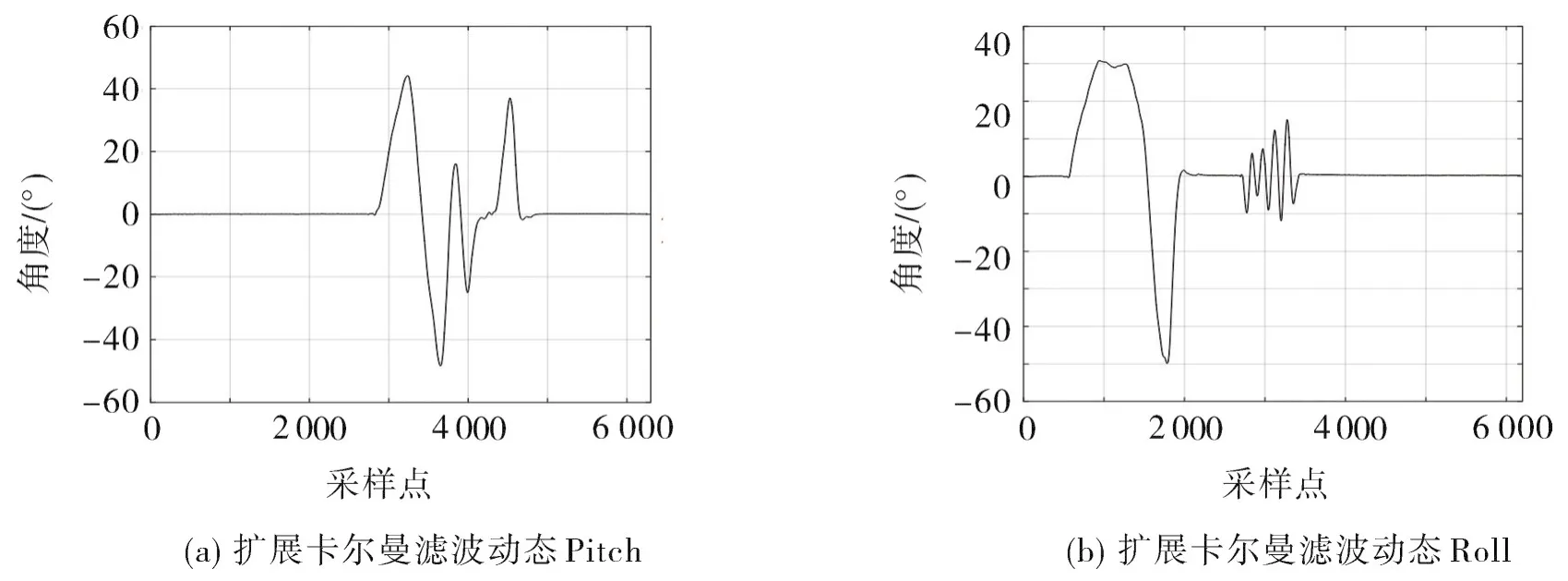
圖10 擴展卡爾曼濾波融合姿態解算的姿態角動態結果Fig.10 Dynamic results of the attitude angle of extended Kalman filter fusion attitude solution

從圖9，10可看出：擴展卡爾曼濾波融合姿態解算的效果比互補濾波解算的效果更好、精度更高，靜態時，俯仰角的解算范圍在(-0.07°，+0.13°)，橫滾角的解算范圍在(-0.04°，+0.15°)，姿態角的解算幅度在0.2°以內，解算精度有很大提高；與互補濾波解算效果相比，動態時，解算的姿態角曲線更為平滑，毛刺部分得到有效消除，穩定性更高，響應速度和收斂速度更快，能夠實時追蹤飛行器的當前姿態角。

5 結 論

針對飛行器飛行時機身抖動對加速度計傳感器產生較大的高頻噪聲干擾，采用基于RBF神經網絡的非線性高頻濾波算法，并結合互補濾波算法對飛行器的姿態角進行擴展卡爾曼濾波的融合姿態解算。實驗表明：擴展卡爾曼濾波的融合姿態解算算法對高頻噪聲有很好的抑制作用，提高了加速度計對姿態的測量精度以及飛行控制系統中姿態解算算法的解算精度，使得解算出的姿態角精度得到有效提高且在長時間范圍內穩定性更強。