船舶動力定位控制系統的非線性觀測器設計

陳勇嘉 楊宣訪 王永建

（海軍工程大學電氣工程學院 武漢 430033）

1 引言

動力定位（DP）［1］是指船舶不借助錨泊，僅通過自身安裝的推進器來抵抗風、浪、流等環境干擾的影響，實現其在海面上固定位置或預期航跡的保持。環境干擾對船舶的影響可以分為由風、流和二階波浪導致的低頻運動，和由一階波浪導致的高頻運動。其中高頻運動只引起船舶的周期性振蕩而不會造成船體大范圍偏離平衡位置，為避免能量浪費和推進器磨損，而盡量不響應一階波浪、噪聲等高頻振蕩干擾信號的作用，這就需要根據傳感器測量的信息和船舶動力定位控制的數學模型估計出船舶的低頻運動狀態，因此狀態估計方法在動力定位控制系統的設計中具有非常重要地位，是動力定位控制系統的關鍵技術之一［2］。

DP系統從20世紀60年代開始應用在海洋船舶上，采用了陷波濾波器，其結構簡單，易于實現，但是會產生相位滯后，使系統穩定性變差。20世紀80年代后，第二代DP系統中經常采用卡爾曼濾波器，該方法的主要缺點是必須將船舶運動的動力學方程在一些給定的艏搖角度值上線性化，由于系統擁有15個狀態變量，所以采用上述方法時系統在線計算量大，而且其中的很多協方差值也很難調整，不利于實現［3～5］。

為了避免動力定位系統采用上述卡爾曼濾波器時所帶來的問題，本文設計了一種基于無跡卡爾曼濾波器的改進算法對模型中的非線性函數的概率密度分布進行擬合，用一系列確定樣本來逼近狀態的后驗概率密度，而不是對非線性函數進行線性化近似，因此對于非線性分布的統計量具有較高的計算精度。該濾波器的有效性通過仿真實驗得到了驗證。

2 基本的數學模型

2.1 船舶低頻運動方程

船舶在海洋中的運動有六個自由度，而水面動力定位作業主要研究船舶的三自由度運動，即縱蕩、橫蕩和艏搖。為描述船舶在水平面的運動，必須建立兩個坐標系統［6～7］：慣性坐標系和隨船坐標系，如圖1所示，定義向量 η=[x，y，ψ ]T表示慣性坐標系下船舶的縱蕩、橫蕩位置和艏搖角度，ν=[u，v，r]T表示隨船坐標系下船舶的縱蕩、橫蕩速度和艏搖角速度，兩坐標系的相互轉換關系為［8］

式中：轉換矩陣

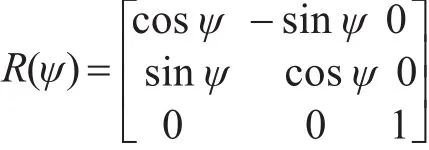
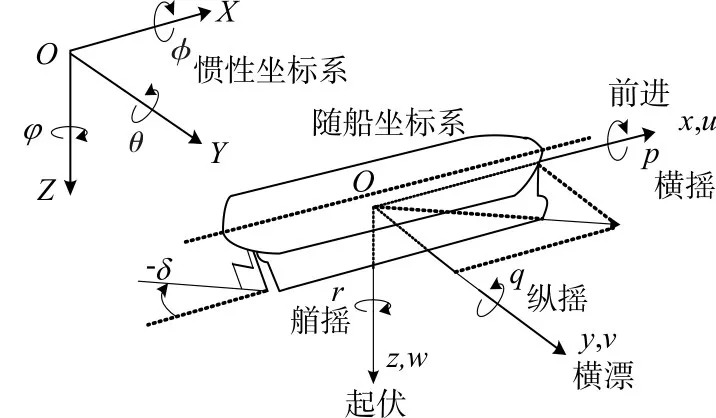
圖1 固定坐標系和隨船坐標系

由文獻［8］可以得到船舶低速運動情況下的低頻運動方程：

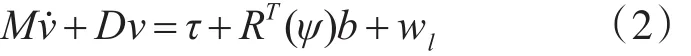
式中：M∈R3×3表示系統慣性矩陣，D∈R3×3為線性水動力阻尼系數。τ∈R3表示控制力和力矩，b∈R3表示由風、浪、流引起的環境力，wl∈R3為過程噪聲向量。

2.2 高頻運動模型

船舶的高頻運動主要是由于一級波浪擾動引起的，可看作是在縱蕩、橫蕩和艏搖三個方向上附加了阻尼的二階諧波振蕩器：

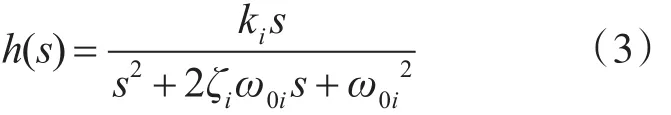
式中，參數 ki與海況有關，ζi(i=1，2，3)為相對阻尼系數，通常取值為 0.05～0.3，w0i(i=1，2，3)為波浪P-M譜中與有義波高相關的海洋主導角頻率。

將上式轉換為狀態空間形式，可以得到船舶的高頻運動模型：

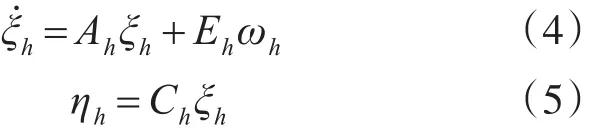
式中 ξh=[ξx，ξy，ξφ，xh，yh，ψh]T

表示船舶在3個自由度方向上的位置和速度信號；wh為零均值高斯白噪聲，wh=[wxwywφ]；ηh為三維列向量，分別表示高頻運動的縱蕩、橫蕩和艏搖角度；其它系數為

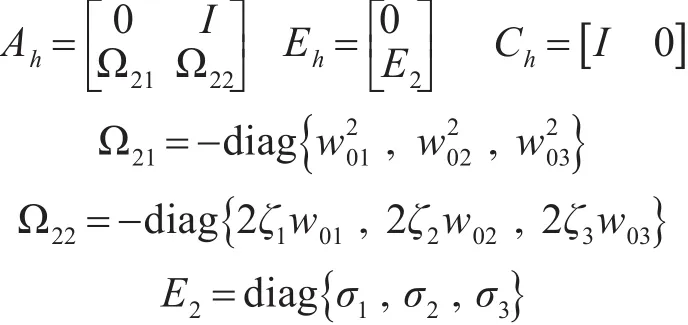
其中σi(i=1，2，3)為與波浪強度有關的常數。

2.3 環境作用力模型

環境力通常是指風、二階波浪漂力、流對船舶的作用力。環境力模型由高斯—馬爾科夫過程表示：

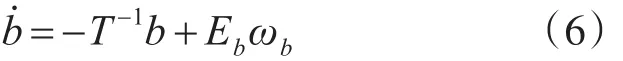
式中：b∈R3表示環境力和力矩；T為包含時間常數的的三維對角矩陣；Eb∈R3×3為噪聲幅值矩陣；ωb∈R3為零均值高斯白噪聲向量。

2.4 總系統模型

由前面的敘述可得系統的測量模型：

式中：vy∈R3為零均值高斯白噪聲。

根據上述模型，綜合得到總的動力定位船舶的數學模型：

3 非線性估計濾波器的設計

3.1 基本原理

基于無跡卡爾曼濾波的改進算法避免了對非線性系統線性化，而是在估計點附近進行UT變換，使用無跡變換來處理均值和協方差的非線性傳遞問題，將先驗狀態估計的Sigma點應用到測量更新中［9］。

3.2 基于無跡卡爾曼濾波的計算步驟［10］

1）初始化：給定系統狀態的均值xˉ和方差P。

2）計算2n+1個Sigma采樣點，這里的n指的是狀態的維數：

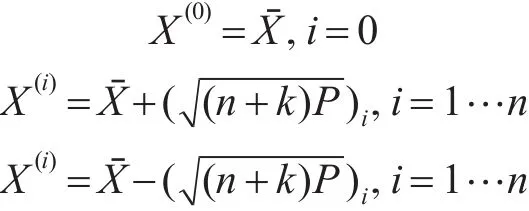
3）計算這些采樣點相應的權值

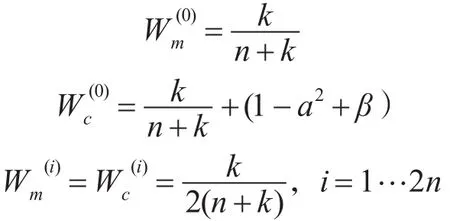
式中，小標m為均值，c為協方差，上標為第幾個采樣點。參數k是一個縮放比例因數，用來降低總的預測誤差，a的選取控制了采樣點的分布狀態，待選參數β≥0是一個非負的權系數，它可以合并方程中高階項的動差，這樣就可以把高階項的影響包括在內。

4）時間更新方程

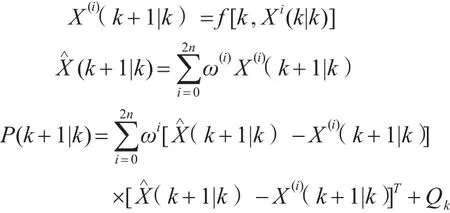
式中，f(·)表示非線性過程，Qk為過程噪聲在k時刻的方差。

5）根據一步預測值，再次使用UT變換，產生新的Sigma點集。

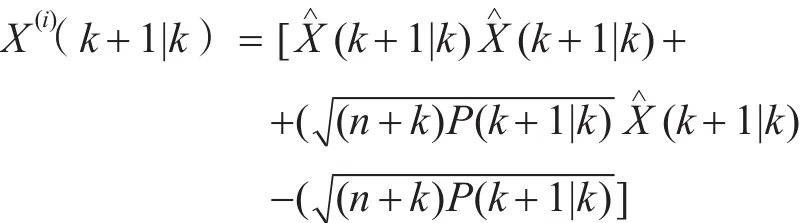
6）測量更新方程

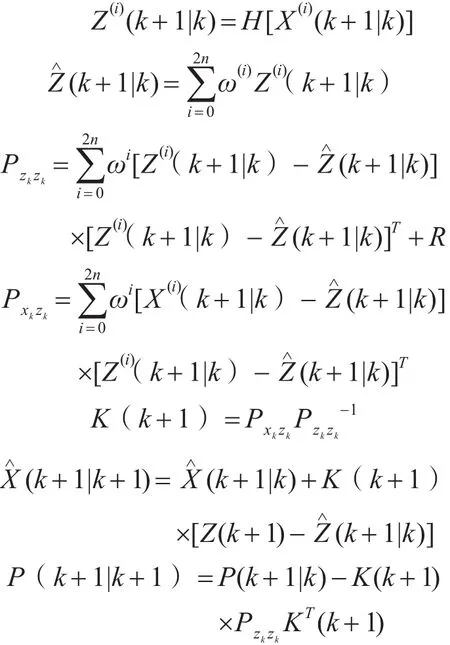
其中，Zk為k時刻的觀測值，H為觀測矩陣，R為測量噪聲的方差，K為卡爾曼增益。

3.3 基于無跡卡爾曼濾波器的設計

3.2 節中給出了算法流程，要把該算法應用到船舶動力定位系統中，需要確定算法中的時間更新方程和測量更新方程的第一個式子，這兩個式子分別與總模型中的狀態方程和觀測方程相對應，基于無跡卡爾曼的改進算法在Matlab（R2013a）/Simu?link中搭建［11］并進行仿真實驗。

圖2中，Subsystem子系統是環境作用力模型，Subsystem1子系統是高頻運動模型，J和J1是S-function模塊。

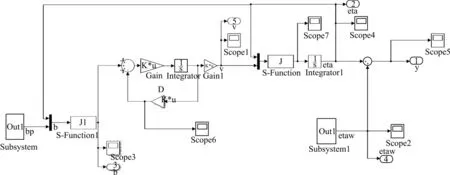
圖2 船舶動力定位系統Simulink模型

4 仿真與分析

為了驗證算法的有效性，對非線性濾波算法進行仿真并與傳統的卡爾曼濾波算法進行對比。本文在MATLAB（R2010a）軟件上進行仿真實驗，以某動 力 定 位 船 舶 為 例［12］：長 L=175(m)，重m=2.461×104(kg)，慣性矩陣M 和線性阻尼陣 D取值如下：

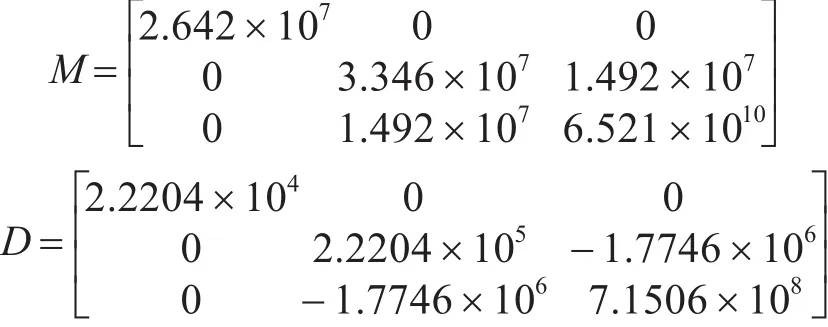
環境擾動作用力模型中的時間參數選為：T=diag(1000 1000 1000)，波浪主頻率、相對阻尼系數和波浪強度為：w0i=0.9，σi=0.6083，ζi=0.3。

所以高頻運動模型中的系數矩陣取值為：

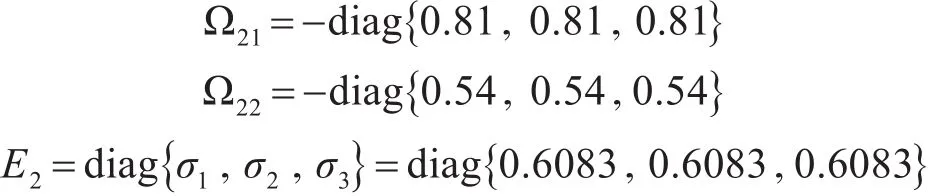
仿真時間為1000s，船舶運動和無跡卡爾曼濾波器對船舶縱蕩、橫蕩和艏搖方向位置的濾波效果如圖3～4所示。

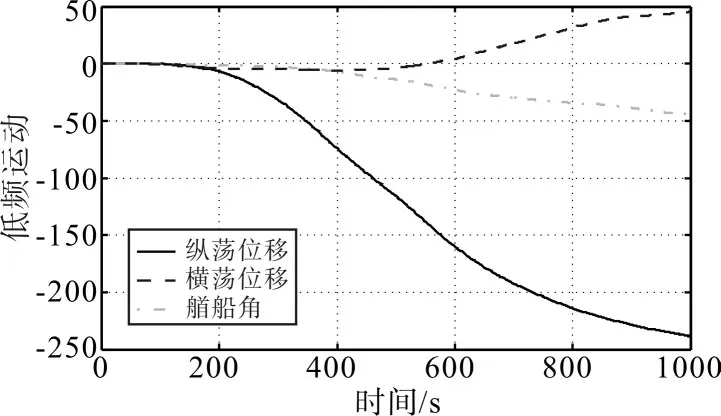
圖3 船舶的低頻運動

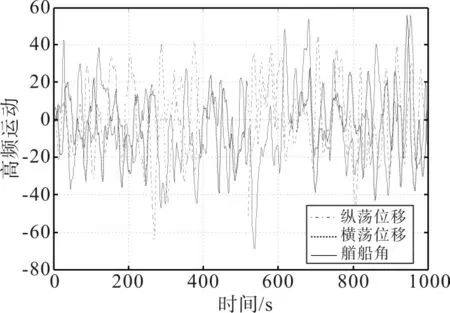
圖4 船舶的高頻運動

圖5 、圖6和圖7為使用傳統的卡爾曼濾波時，船舶的縱向位移、橫向位移和艏向角的真實值和估計值。圖8、圖9和圖10為使用非線性濾波器時，船舶的縱向位移、橫向位移和艏向角的真實值和估計值。從仿真結果可以看出，非線性濾波器從附有噪聲和高頻運動分量的綜合輸出中能夠較好地濾除高頻運動部分，圖8～圖10估計值較好地從真實值中估計出，使動力定位船舶能夠得到有效的控制，減少不必要的能量損失。

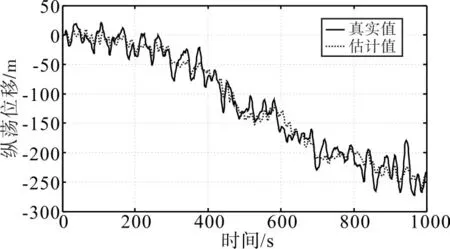
圖5 縱向位移真實值和估計值

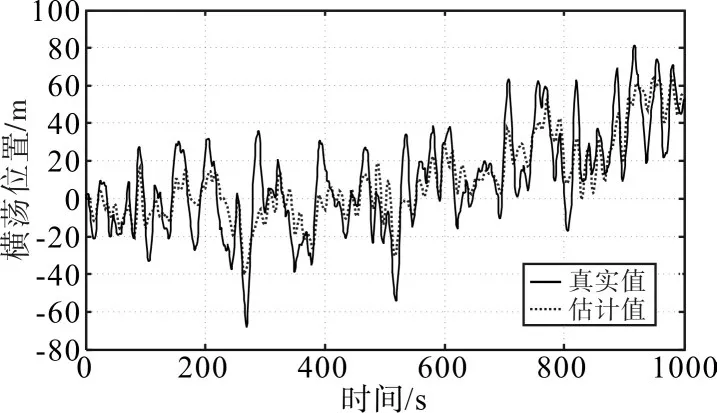
圖6 橫向位移真實值和估計值

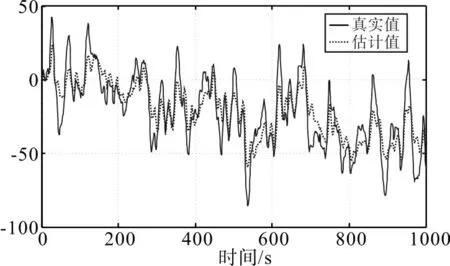
圖7 艏搖方向真實值和估計值

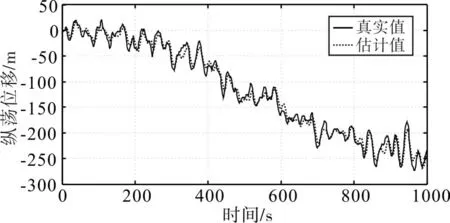
圖8 縱向位移真實值和估計值

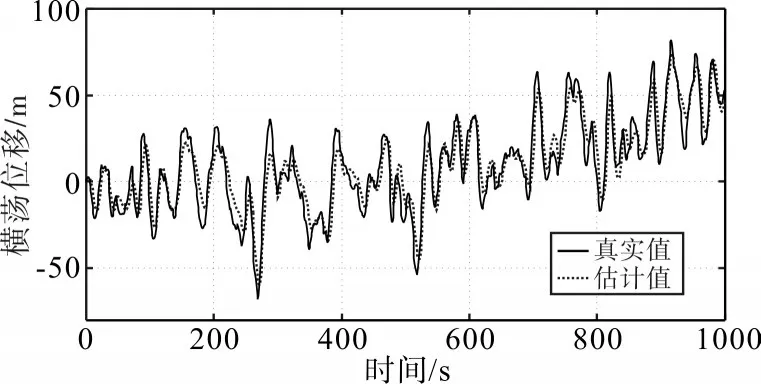
圖9 橫向位移真實值和估計值

圖10 艏搖方向真實值和估計值

5 結語

本文針對船舶動力定位控制系統設計了一種基于無跡卡爾曼濾波器的非線性觀測器，該觀測器的優點是摒棄了對非線性函數線性化的傳統做法，使用無跡變換來處理均值和協方差的非線性傳遞問題。仿真結果表明，該非線性觀測器可以較好地估計船舶運動的各狀態值，適用于動力定位系統。

［1］邊信黔，付明玉，王元慧.船舶動力定位［M］.北京：科學出版社，2011：8-10.

［2］Tomera，Miroslaw.Nonlinear observers design for multi?variable ship motion control［J］.Polish Maritime Re?search，2012，19（S1）：55-56.

［3］Grimble M J，Patton R J，Wise D A．The Design of Dy?namic Ship Positioning Control Systems Using Extended Kalman Filtering Techniques ［C］//Oceans， 2011：488-497.

［4］J LI，G xia.The application of an extended Kalman filter in the dynamic positioning system［C］//International Con?ference on Natural Computation，2016：1945-1946.

［5］何黎明，田作華，施頌椒.動力定位船舶的非線性觀測器設計［J］.上海交通大學學報，2003，37（6）：964-965.

［6］Bui VP，Ji SW.Nonlinear observer and sliding mode con?trol design for dynamic positioning of a surface vessel［C］// International Conference on Control， 2012：1900-1904.

［7］Du JL，Wang SY，Zhang XK.Nonlinear observer design for ship dynamic positioning system［J］.Ship engineer?ing，2012，34（3）：307-312.

［8］Thori.Fossen，Tristan Perez.Kalman Filtering for Position?ing and Heading Control of Ships and Offshore Rigs［J］.IEEEControl Systems Magazine，2009，29（6）：32-46.

［9］丁浩晗，馮輝等，基于自適應無跡卡爾曼濾波的動力定位估計狀態［J］.大連海事大學學報，2016，42（2）：242-246.

［10］［美］Dan Simon.最優狀態估計—卡爾曼，H∞及非線性濾波［M］.張勇剛，李寧，奔粵陽，譯.北京：國防工業出版社，2013：334-336.

［11］黃小平，王巖.卡爾曼濾波原理及應用—MATLAB仿真［M］.北京：電子工業出版社，2015：103-105.

［12］Saelid S，Jenssen N，Balchen J.Design and analysis of a dynamic positioning system based on Kalman filtering and optimal control［J］.Automatic Control IEEE Trans?actions on，1983，28（3）：331-339.