諧振子耦合型熱聲驅動脈管制冷機研究

胡江風 胡劍英 徐靜遠 王 瑋 羅二倉

（1中國科學院理化技術研究所 北京 100190；2中國科學院大學 北京 100049）

熱聲效應即熱能與聲能之間的相互轉換。它的兩個重要應用是熱聲發動機和脈管制冷機。在熱聲發動機中，通過加熱器對氣體加熱，系統內產生自激的壓力振蕩，熱能被轉換為聲能；在脈管制冷機中，聲功在回熱器內將熱量從低溫端搬運到高溫端被消耗。熱驅動熱聲制冷機就是將熱聲發動機和脈管制冷機結合起來，組成一種除振蕩氣體外沒有運動部件的系統［1-4］。這種系統具有機械結構簡單、可靠性高、工作氣體為環境友好的惰性氣體、壽命長等優點，此外它的外燃機可以由各種熱源（例如廢熱和太陽能等）驅動，因此成為近幾十年來國內外研究的熱點。

1990年，R.Radebaugh等［5］首次提出熱聲驅動低溫制冷機的結構獲得了90 K的制冷溫度。1998～2000年，以液化天然氣為目標的大型熱驅動制冷系統建成，在150 K的制冷溫度下產生3 800 W制冷量，相當于1 324.89 L/d的天然氣液化率［6］。上述早期熱聲驅動低溫制冷機中，包括行波發動機和駐波發動機驅動的熱聲制冷機，均沒有特別考慮將發動機和制冷機耦合問題，二者都是通過短管和閥門簡單連接在一起。2005年，胡劍英等［7］對熱聲發動機驅動脈管制冷機的耦合機理進行了一系列研究，提出了聲學變壓器的結構。戴巍等［8-11］進行了用聲學壓力波放大器耦合熱聲驅動低溫制冷機的研究。2007年，胡劍英等［12］研究了雙介質聲壓放大器耦合的熱聲驅動兩級脈管制冷機，該系統在國際上首次突破了液氫溫度。這一階段的研究雖然考慮了耦合過程，但系統都具有較大體積的諧振結構，緊湊性差而且整機 效率仍較低，限制了進一步應用。2010年，K.D.Blok［13］提出了四級熱聲發動機系統，系統緊湊型具有較大的提高。2013年，羅二倉等［14］研究了環路多級行波熱聲發動機旁接驅動脈管制冷機系統，在130 K天然氣液化溫區下獲得1 200 W冷量及8%的整機

效率，2014年，張麗敏等［15］提出了一種環路多級熱驅動并聯型脈管系統，熱聲發動機和脈管制冷機通過長管連接，相比于旁路結構能夠有效回收制冷機熱端的聲功，效率更高。上述研究中，制冷機通過短管旁接或者通過長管串接在發動機環路中，雖然保持了熱驅動脈管制冷機的無運動部件的特性，但系統仍然體積較大且有很大的聲功損失，很難達到發動機和制冷機最佳耦合的要求，限制了整機的 效率。

2016年，胡劍英等［16］提出采用運動活塞耦合連接熱聲發動機和制冷機的新方式，該系統利用壓縮機輸入少量聲功，聲功在熱聲發動機中被放大，再通過活塞進入脈管制冷機中進行制冷，活塞起到傳遞聲功并且耦合發動機和制冷機的作用。基于此，本文采用SAGE軟件對該系統進行模擬計算。首先，分析了諧振子耦合機理，并對諧振子的結構進行了優化設計。然后，重點討論了關鍵工況參數對系統性能的影響。最后，將諧振子與長管兩種耦合結構的熱驅動制冷機性能進行對比。

1 系統介紹

諧振子耦合的熱驅動脈管制冷機如圖1所示，由直線壓縮機、熱聲發動機、諧振子、脈管制冷機、慣性管和氣庫組成。其中，熱聲發動機由室溫端主換熱器、回熱器、高溫端換熱器、熱緩沖管以及室溫端組成，脈管制冷機由室溫端主換熱器、回熱器、低溫端換熱器、脈管以及室溫端組成，采用諧振子耦合熱聲發動機和脈管制冷機。脈管制冷機回熱器相位由慣性管和氣庫調節。整機工作原理為：直線壓縮機活塞往復運動使氣體工質振蕩而輸出聲功，直線壓縮機的工作頻率可以根據設計人為設定，輸出的聲功大小也可以人為調節；直線壓縮機產生的聲功首先進入到熱聲發動機，由于發動機的高溫端換熱器向系統輸入加熱量，回熱器內形成了正向的溫度梯度，因此聲功在熱聲發動機的回熱器中被放大；從熱聲發動機室溫端出來的聲波由于諧振子的機械阻尼作用會被消耗掉很小的一部分能量，同時相位被調整后進入脈管制冷機中；聲波在脈管制冷機回熱器由于泵熱產生制冷量而消耗掉大部分的能量，剩余聲功在慣性管、氣庫內被完全消耗。該系統通過諧振子來給發動機調相，使發動機獲得最優的熱聲轉化效率，同時將放大后的聲功傳遞給脈管制冷機中產生制冷量。

2 諧振子的耦合機理與優化設計

2.1 諧振子耦合機理

圖2所示為諧振子耦合機理，諧振子活塞分為前活塞與后活塞，兩活塞采用間隙密封，面積相等或不相等。前活塞安裝在發動機出口，后活塞位于脈管制冷機入口，工作時熱聲發動機的壓力波動作用在大活塞上，推動大活塞往復運動，作用在大活塞上的力通過連接桿傳到小活塞上，中間連接桿由板簧定位和支撐，最后使得整個活塞和連桿一起做往復運動。兩個活塞之間的氣缸容積為空容積，兩不等面積活塞運動時氣缸容積變化影響氣缸內氣體的壓力波動，所以氣缸內空容積充當一個氣體彈簧的作用，當一定的壓力波動作用推動前活塞運動時，后活塞同時產生壓力波，向制冷機輸入聲功，這就是聲功傳遞過程。為了獲得好的耦合效果，其中一個最關鍵的因素就要在熱聲發動機回熱器內獲得理想相位關系，即壓力與速度之間的相位差為零的行波聲場；對應的在發動機出口處壓力與速度之間的相位差要滿足特定的關系。本設計的諧振子通過調節活塞的面積、質量和彈簧剛度，使得發動機出口處壓力與速度的相位差滿足特定關系，進而在回熱器獲得行波聲場，從而使此時發動機的熱聲轉化效率最高。以上是關于諧振子耦合原理的簡單解釋。

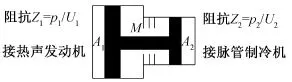
圖2 機械諧振子耦合機理Fig.2 The coupling mechanism of mechanical resonator

在計算模型中，將諧振子模型的主要部件簡化為活塞、板簧以及阻尼，分別提供諧振子耦合熱驅動發動機和制冷機所需的聲感、聲容、機械阻尼特性。根據諧振子力平衡可得式（1）：

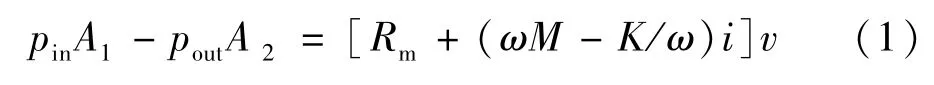
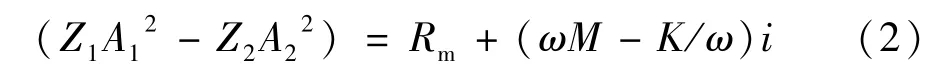
式中：p為壓力波動，Pa；U為體積流率，m3/s；v為振子運動速率，m/s；A為活塞橫截面積，m2；K為彈性剛度（包括氣體彈性系數與機械彈性系數），kN/m；M為振子動質量，kg；Rm為等效機械阻尼，N·s/m；ω為角頻率，rad/s；Z為聲阻抗，Pa·s/m3。

在系統工作頻率不變的情況下，諧振子活塞面積和機械阻尼影響阻抗實部，而活塞面積、振子質量、彈性剛度影響阻抗虛部。因此，諧振子出入口的阻抗由活塞橫截面積、彈性剛度、動質量以及機械阻尼決定。系統工作頻率設定為55 Hz，角頻率為345.6 rad/s。計算中彈性剛度為80 kN/m，機械阻尼為50（N·s）/m。將活塞面積、動質量作為優化變量，優化目標是使耦合熱驅動脈管制冷機整機達到最高 效率，同時諧振子本身消耗聲功最少。

2.2 計算模型

本系統模型設計基于實驗室現有的一臺熱聲發動機和工作在80 K溫區的單級脈管制冷機，其設計工況和結構參數如表1、表2所示。

表1 系統設計工況Tab.1 System design conditions

表2 系統結構參數Tab.2 System configuration parameters

模擬計算基于SAGE軟件展開，SAGE采用圖形 化界面，對各個部件分別建模。各模塊之間通過質量、壓力、能量進行銜接，可實現整機模擬與連續求解。系統性能通過諧振子損失聲功量、制冷量及 效率等綜合體現。熱聲發動機的熱聲轉化效率ηengine，脈管制冷機的 效率ηptc、整機 效率ηoverall、熱致冷

效率ηhcool分別為：

式中：Win為直線壓縮機輸入系統的聲功，W；Wout為發動機出口的聲功，W；Winc為輸入脈管制冷機的聲功，W；Th為高溫，K；T0為室溫，K；Tc為制冷溫度，K；Qhot為加熱量，W；Qc為整機制冷量，W；Qc0為假設脈管制冷機輸入聲功為Win效率為ηptc時所能產生的制冷量，W。ηhcool表示在除去壓縮機輸入的電功外，發動機熱致聲、諧振子傳遞聲功以及制冷機聲致冷三個過程總的熱致冷 效率。

2.3 諧振子優化設計

根據上述系統參數優化設計諧振子。首先，單獨優化熱聲發動機和脈管制冷機，當熱聲發動機的熱聲效率最高時，獲得發動機的次換熱器端阻抗Z1幅值1.460 ×107（Pa·s）/m3和相位θ1為 54.4°，熱聲發動機效率為50.1%；當脈管制冷機效率達到最高，得到制冷機的主換熱器端的阻抗Z2幅值2.417×107（Pa·s）/m3和相位θ2為 -29.1°，制冷機效率為30.74%。然后匹配耦合熱聲發動機和脈管制冷機，設計中取阻抗Z1、Z2為最優阻抗，探究諧振子不同活塞橫截面積以及動質量下系統性能。下面分諧振子活塞面積相等和不相等兩種情況進行討論。

2.3.1 諧振子活塞等面積計算

首先研究振子活塞等面積的情況，此時有活塞面積和動質量兩個計算參數，式（2）可分解為實部與虛部兩個等式方程（7）、（8），可以驗證參數解唯一或無解。

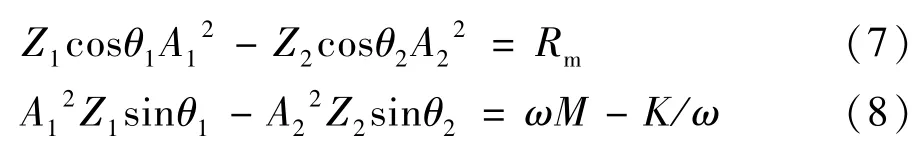
將上述經驗值和阻抗Z1、Z2代入式（7）、式（8）中發現，無論活塞面積A取何值，實部等式（7）無法成立。說明諧振子活塞等面積時，熱聲發動機出口和脈管制冷機入口無法同時達到最優阻抗值，此時耦合熱驅動制冷機不能達到最高效率。

2.3.2 諧振子活塞不等面積計算

當前后活塞直徑D1、D2不相等時，存在3個計算參數D1、D2和M，理論上有無窮多個參數解，在SAGE軟件計算結果如表3所示。

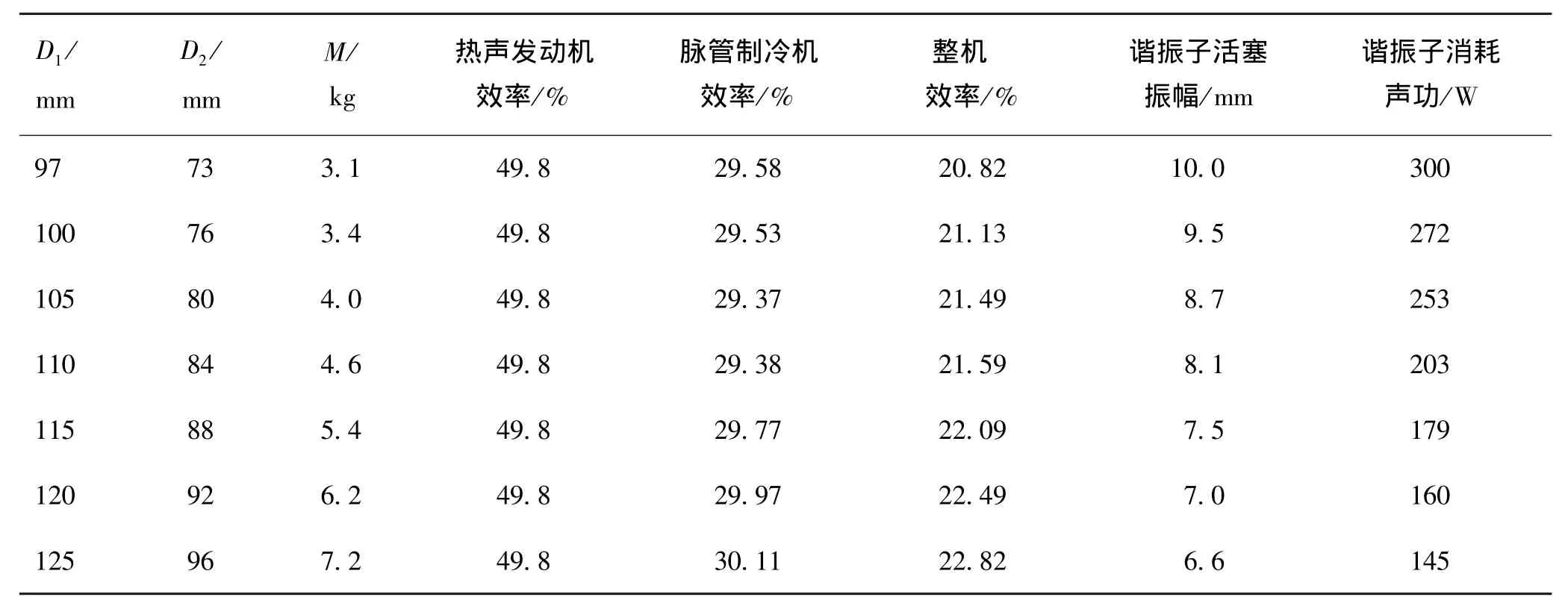
表3 諧振子活塞不等面積時計算結果Tab.3 Calculation results of the resonator piston when the area is not equal

結果表明，存在無窮多個參數組合使阻抗Z1、Z2達到單獨優化時的最優幅值，此時熱聲發動機和脈管制冷機效率均接近最高。在表中所示的各計算組合中，3個參數的增減趨勢相同。雖然不同組合都能使熱聲發動機和脈管制冷機的效率接近最高，但諧振子消耗聲功也對脈管制冷機的效率和整機 效率有較大影響。隨著3個參數值的增加，諧振子等效機械阻尼減小，因此消耗的聲功減小，脈管制冷機的效率和整機 效率升高。考慮到諧振子的實際因素，較大的動質量、活塞直徑及活塞振幅均不利于系統運行，所以在保證整機 效率較高的前提下，選取其中一組參數作為最終設計：D1＝120 mm，D2＝92 mm，M＝6.2 kg。

2.4 整機性能

確定諧振子的結構后，對整個系統進行模擬計算，獲得諧振子耦合型熱驅動脈管制冷機的性能參數如表4所示。此時直線壓縮機的輸入聲功為877 W，工作頻率為55 Hz；熱聲發動機的高溫端換熱器在900 K溫度輸入熱量為2 372 W，熱聲轉化效率為49.8%，發動機將聲功放大2.5倍后輸出聲功為2 053 W；經過諧振子聲功傳遞的機械損失為160 W，輸入脈管制冷機的聲功為1 893 W，在脈管制冷機低溫端80 K溫區產生209 W的制冷量；最終的整機效率達到22.5%，僅由熱致冷的 效率為17.3%。

表4 諧振子耦合型熱驅動脈管制冷機性能Tab.4 Performance of the coupling in a thermoacoustic driven pulse tube refrigeration

3 重要參數對系統性能的影響

3.1 加熱溫度的影響

保持系統直線壓縮機工作的活塞振幅不變，低溫端溫度在80 K，改變熱聲發動機熱端的加熱溫度從373 K增加到923 K，研究系統中主要參數隨加熱溫度變化的關系。圖3所示諧振子消耗聲功與制冷量隨加熱溫度的變化。總體上，隨著加熱溫度升高時，制冷量和諧振子消耗聲功均增加。其中，加熱溫度從373 K升高到923 K，系統制冷量由135 W增加到211 W。圖4所示系統各效率隨加熱溫度的變化關系。可知發動機熱聲轉化效率和系統熱致冷 效率都隨溫度增加逐漸升高，其中加熱溫度從400 K增加430 K左右，熱聲轉化效率和熱致冷 效率依次由負變正。可推斷400 K左右溫度發動機產生聲功開始放大，430 K左右輸入的熱量開始產生制冷量。隨著加熱溫度的增加（壓縮活塞掃氣量保持不變），壓縮機輸入發動機的聲功Win逐漸變小，最終輸入到脈管制冷機入口的聲功Wout并沒有顯著增加，結果顯示制冷機的效率從29.4%增加到30.1%，相應的整機效率從21.5%加到22.4%。

3.2 制冷溫度的影響

同樣保持直線壓縮機的活塞振幅不變，發動機加熱端溫度為900 K，改變制冷溫度從80 K增加到150 K，考察整機性能隨制冷溫度變化。由圖5可知，諧振子消耗聲功與制冷量都隨制冷溫度的增加而增加，制冷量增長顯著，制冷溫度從80 K升高到150 K，對應產生的制冷量由209.3 W增加到626.5 W。圖6所示為發動機熱聲轉化效率、脈管制冷機效率、熱致冷 效率與整機 效率隨制冷溫度變化的關系。可知發動機效率隨之制冷溫度增加而緩慢增長；脈管制冷機效率、熱致冷 效率和整機 效率先略增高升高后降低，在90 K左右獲得峰值效率，而且在80～110 K范圍內，系統各效率均保持較高值。

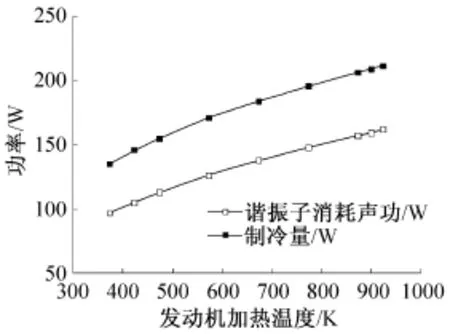
圖3 系統各功率隨加熱溫度的變化Fig.3 The variation of the power of the system with heating temperature

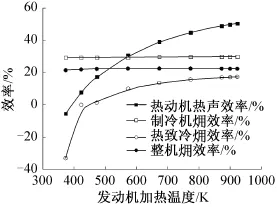
圖4 系統各效率隨加熱溫度的變化Fig.4 The variation of the efficiency of the system with heating temperature

3.3 等效機械阻尼的影響

諧振子作為一個機械運動部件自身會損失一部分聲功，等效機械阻尼是對諧振子動力學損失的集總表征，包括摩擦損失、氣體拖曳損失和板簧形變發熱損失等。它不僅影響諧振子聲功損失，同時影響諧振子運動特性。實際中諧振子機械阻尼受加工工藝的影響較難確定，一般根據工程經驗估計大致范圍。圖7和圖8所示，保持系統熱聲發動機熱端900 K加熱溫度，脈管制冷機冷端80 K的制冷溫度，其他參數不變，將等效機械阻尼在0.001～50 N·s/m經驗范圍內變化，研究其對系統性能的影響。由圖7可知，隨著機械阻尼的增大，整機各個效率都呈下降趨勢。主要原因是在圖8中機械阻尼的增大使得諧振子消耗的聲功從20 W至160 W迅速增長。其中熱致冷 效率下降較為明顯，從20%降低到17%，可以看出，通過各種途徑減小機械阻尼可以提高熱致冷 效率。

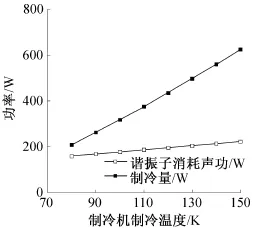
圖5 系統各功率隨制冷溫度的變化Fig.5 The variation of the power of the system with cooling temperature

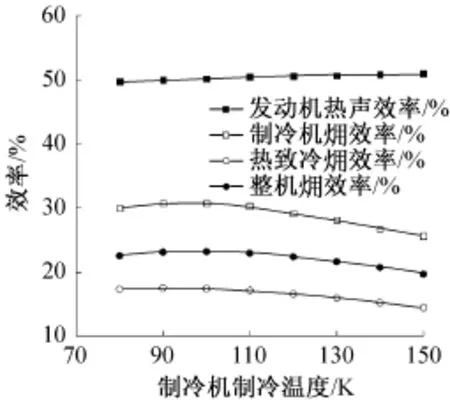
圖6 系統各效率隨制冷溫度的變化Fig.6 The variation of efficiency of the system with cooling temperature

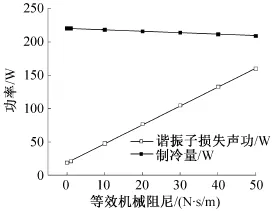
圖7 等效機械阻尼變化對系統各功率參數的影響Fig.7 Effect of equivalent mechanical damping on the power parameters on the system

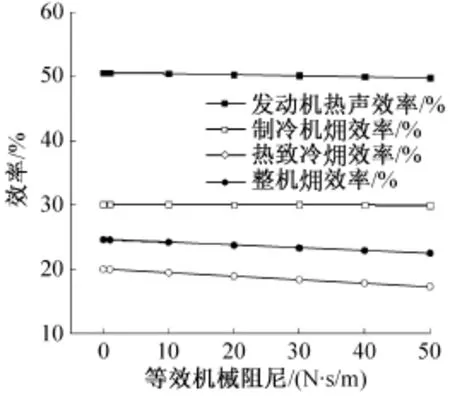
圖8 等效機械阻尼變化對系統各效率的影響Fig.8 Effect of equivalent mechanical damping on the efficiency in the system

4 兩種耦合方式的對比

長管耦合是使用一段長管連接發動機和制冷機，由于其聲學特性，長管能夠傳遞聲功同時改變阻抗幅值與相位。但是不可避免的是耦合長管的聲功損失較大，并且耦合后的發動機和制冷機難以達到最佳的工作狀態。為了證明這一點，將諧振子耦合型與長管耦合型兩種方式進行對比研究。

在對長管耦合型系統模擬中，保持運行工況參數與上述諧振子耦合型系統相同，優化長管的尺寸使系統效率達到最高；最終優化后的長管直徑為13.8 mm，長度為3.7 m。對比兩種耦合機構系統分別獲得最優化的性能如表5所示。

由表5可知采用諧振子耦合系統，能獲得更多制冷量和更高系統效率，性能明顯優于長管耦合的方式。這主要是由于兩方面因素引起：一是長管耦合比諧振子耦合消耗聲功更多，由下表模擬計算數據顯示前者是后者的4倍；二是長管無法使熱聲發動機出口端阻抗達到最優，因此不能獲得最高效率。綜上所述，采用諧振子作為耦合機構能夠獲得更好的系統性能。

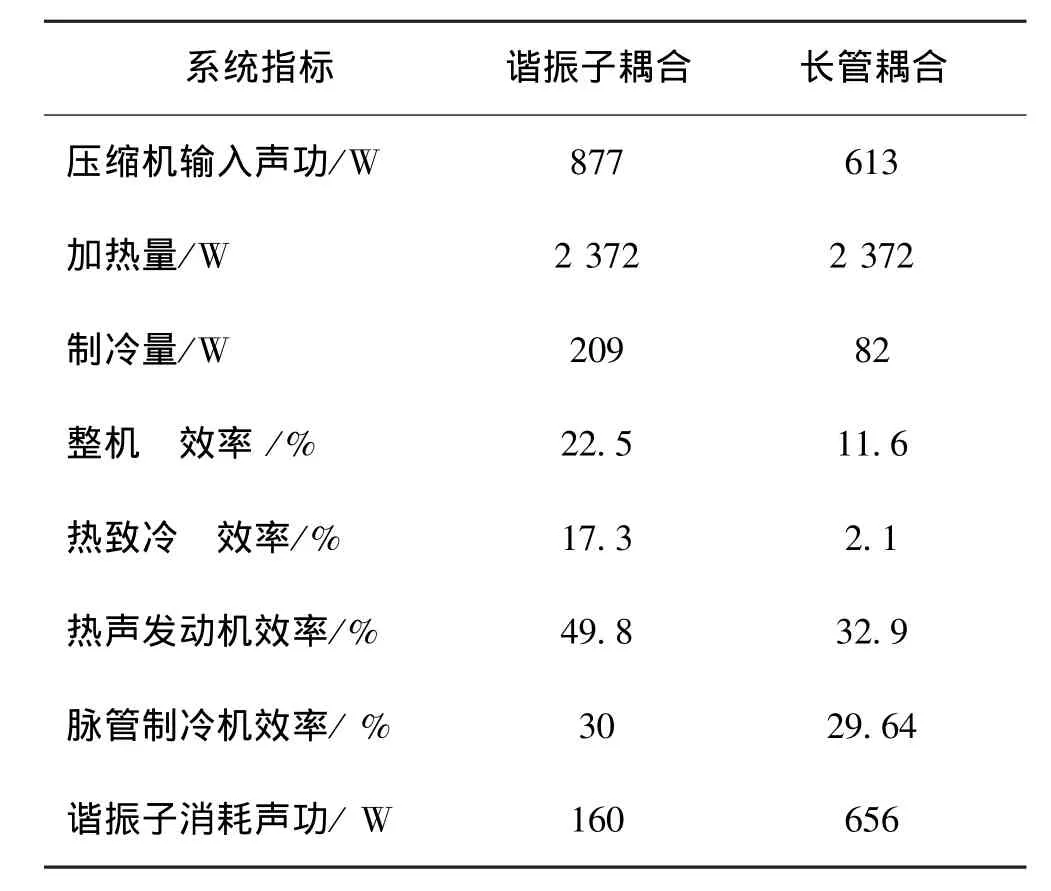
表5 兩種耦合機構的系統最優性能對比Tab.5 Optimal performance comparison of the two coupling method

5 結論

本文基于SAGE軟件對諧振子耦合型熱驅動脈管制冷機系統進行了模擬計算。研究表明：當諧振子兩端面積不相等時可以更好地匹配發動機和制冷機，系統能夠獲得最高效率；制冷溫度在80～110 K溫區內系統各效率都保持較高；減小機械阻尼可以有效提高系統熱致冷 效率；相比長管耦合方式，本文提出的諧振子耦合聲功傳遞損失更小，整機 效率更高，是一種更為理想的耦合方式。

［1］SWIFT G W，GARRETT S L.Thermoacoustics： a unifying perspective for some engines and refrigerators［J］.Journal of the Acoustical Society of America，2003，113（5）：2379-2381.

［2］梁驚濤.脈沖管制冷的理論和實驗研究［J］.制冷學報，1996，17（3）：1-7. （LIANG Jingtao.Study and experimental study on pulse tube cooling ［J］.Journal of Refrigeration，1996，17（3）： 1-7.）

［3］宣戰北，王俊杰，周遠.低溫箱的新冷源：脈沖管制冷機［J］.制冷學報，1992，13（1）：33-37.（XUAN Zhanbei，WANG Junjie，ZHOU Yuan.New cold source of cryogenic box： pulse tube chiller［J］.Journal of Refrigeration，1992，13（1）： 33-37.）

［4］劉少帥，張華，張安闊，等.80 K脈管制冷機慣性管調相機理及優化研究［J］.制冷學報，2016，37（5）：100-105.（LIU Shaoshuai，ZHANG Hua，ZHANG Ankuo，et al.Theory and optimization study of inertance tube of 80 K pulse tube refrigerator［J］.Journal of Refrigeration，2016，37（5）：100-105.）

［5］RADEBAUGH R，MCDERMOTT K M，SWIFT G W，et al.Development of a thermoacoustically driven orifice pulse tube refrigerator［C］//Proceeding of the interagency meeting on cryocoolers.Plymouth，MA，1990：205-220.

［6］ARMAN B，WOLLAN J，KOTSUBO V，et al.Operation of thermoacoustic stirling heat engine driven large multiple pulse tube refrigerators［J］.Cryocoolers 13，2005：181-188.

［7］胡劍英，羅二倉，戴巍，等.一種提高熱聲發動機壓比的“聲學變壓器”［J］. 低溫工程，2005（5）：26-29.（HU Jianying，LUO Ercang，DAI Wei，et al.Acoustical transformer capable of improving thermoacoustic pressure ratio［J］.Cryogenics，2005（5）：26-29.）

［8］戴巍，羅二倉，胡劍英，等.用于熱聲驅動脈沖管制冷機的新耦合機制：聲學放大器［J］.科學通報，2005，50（19）：2178-2179.（DAI Wei，LUO Ercang，HU Jianying，et al.New coupling mechanism for thermoacoustic drive pulse tube chiller： acoustic amplifier［J］.Chinese Science Bulletin，2005，50（19）：2178-2179.）

［9］羅二倉，胡劍英，戴巍，等.采用彈性膜片的大壓比熱聲驅動制冷系統：201510064340［P］.2006-03-08.（LUO Ercang，HU Jianying，DAI Wei，et al.Experimental system of large pressure thermal shock driven by elastic membrane： 201510064340［P］.2006-03-08.）

［10］DAI Wei，LUO Ercang，HU Jianying，et al.A heat-driven thermoacoustic cooler capable of reaching liquid nitrogen temperature［J］.Applied Physics Letters，2005，86（22）：224103.

［11］DAI Wei，LUO Ercang，ZHANG Yong，et al.Detailed study of a traveling wave thermoacoustic refrigerator driven by a traveling wave thermoacoustic engine［J］.The Journal of the Acoustical Society of America，2006，119（5）：2686-2692.

［12］HU Jianying，LUO Ercang，DAI Wei，et al.A heat-driven thermoacoustic cryocooler capable of reaching below liquid hydrogen temperature［J］.Science Bulletin，2007，52（4）：574-576.

［13］BLOK K D.Novel 4-stage traveling wave thermoacoustic power generator［C］//ASME 2010，Joint Us-European Fluids Engineering Summer Meeting Collocated with Inter-national Conference on Nanochannels，2010：73-79.

［14］ZHANG L M，HU J Y，WU Z H，et al.A 1 kW-class multi-stage heat-driven thermoacoustic cryocooler system operating at liquefied natural gas temperature range［J］.Applied Physics Letters，2015，107（3）：205-220.

［15］Zhang Limin，Chen Yanyan，Luo Ercang.A novel thermoacoustic system for natural gas liquefaction［J］.Energy Procedia，2014，61：1042-1046.

［16］胡劍英，羅二倉，張麗敏，等.多級熱聲發電機組及具有該機組的多級回熱式制冷系統：201610654353.2［P］.2016-12-07. （HU Jianying，LUO Ercang，ZHANG Limin，et al.Multi-stage thermoacoustic generator and multi-stage regenerativerefrigeration system with thesameunit：201610654353.2［P］.2016-12-07.