微小衛星聯合執行機構的遞階飽和姿態控制方法

華 冰，陳 林，吳云華

（南京航空航天大學，南京 210016）

大角度姿態機動是微小衛星姿態控制中重要功能之一[1]。微小衛星在執行各種復雜的空間任務時（如對地穩定到對日捕獲[5]、對日穩定到對地捕獲[1]、對地面某特定目標進行長時間觀測或攝像[3]、單線陣相機立體成像[4]、增大衛星過境的可觀測范圍及觀測數據量[5]等，），就要求微小衛星在大角度姿態機動過程中不僅能達到較高的指向姿態精度和姿態穩定性，而且要能夠快速機動[1]。傳統的單一執行機構控制方案不能很好地滿足姿態控制系統的要求，需要采用各種聯合姿態控制系統來優化和實現準確跟蹤、高穩定度和快速機動的航天器姿態控制[6]。因此有必要對基于聯合執行機構的衛星大角度姿態機動控制技術進行研究。

聯合執行機構是指兩種及兩種以上的執行機構同時作為航天器姿態機動的執行機構[1]。隨著推進技術的發展，許多衛星都采用聯合執行機構進行大角度姿態控制，如歐空局推出的昴宿星（Pleiades Satellite）、美國“數字地球”研制的World View系列衛星等。印度空間研究機構研制的Carto Sat-2的姿態執行機構采用反作用飛輪（0.3）、噴氣推力器（1），如圖1所示。美國軌道科學公司的華衛2姿態控制方式采用三軸穩定，姿態執行機構有四個反作用飛輪和推力器，如圖 2所示[5]。這些衛星都可以實現大角度快速機動，在軍用和民用方面做出了重要貢獻。

圖1 Carto Sat-2Fig.1 Carto Sat-2

圖2 華衛2Fig.2 Huwei 2

聯合執行機構的概念最早出現在文獻[6]。文獻[7]和文獻[8]提出了基于歐拉旋轉設計反饋控制律進行姿態跟蹤控制，實現了聯合執行大角度姿態控制算法。文獻[9]與文獻[10]提出了一種基于系統狀態的 PD閉環控制器，該控制器通過狀態增益反饋以達到單軸機動的時間最優。文獻[11]提出了繞歐拉軸旋轉的遞階飽和大角度姿態控制算法。文獻[12]提出用推力器提供機動過程中所需的大力矩，同時用動量輪進行高精度的調節，以達到機動過程中的高精度的控制算法。文獻[13]針對聯合執行機構的問題提出了既提高機動速度又提高機動精度實物混合控制算法。文獻[14]提出基于Lyapunov方法設計了相應的控制器，取得了很好的控制效果，但是并沒有解決執行機構力矩及轉速飽和等問題。文獻[15]研究了噴氣系統和多個動量輪聯合的非線性控制，采用的是Rodrigus參數而非四元數。文獻[16]基于噴氣系統和多個反作用輪的姿態控制算法。文獻[17]建立噴氣系統加偏置動量輪的衛星姿態系統模型，進一步設計LQG和Lyapunov控制兩種聯合控制律。文獻[18]的噴氣系統采用的都是 Bang-Bang控制，而文獻[19]對Bang-Bang控制和PWM（脈寬調制）控制進行了對比分析，表明噴氣系統采用PWM更加節省燃料。

在實際小衛星姿態控制系統中，推力器能夠輸出在大角度快速機動過程中所需要的大力矩，但不具備高精度姿態控制的能力。飛輪雖能夠輸出較為精準的控制力矩，并且僅消耗電能，但不能提供快速機動過程中所需要的大力矩，因此有必要結合這兩個執行機構的優點，為微小衛星的大角度快速機動提供大輸出和精度高的控制力矩[9]。由于衛星姿態控制系統是一個復雜的非線性系統，考慮到系統的非線性和復雜程度，又結合實際大角度姿態機動過程中力矩飽和角速度限制的因素，本文首先設計基于歐拉軸轉動的遞階飽和PD姿態機動控制方法，其次在PD控制律的基礎上，提出基于歐拉軸轉動的模糊PD控制律。執行機構采用冷氣推進系統和反作用飛輪來提供大且精確的控制力矩，其中噴氣系統采用PWM波控制。本文采用的飛輪最大輸出力矩0.005，當所需力矩超過0.005時，需冷氣推力器提供所需力矩，從而保證姿態機動快速精確的進行。最后將提出的控制策略應用于微小衛星大角度姿態機動控制中，仿真結果表明模糊控制更適合非線性系統的環境，可使衛星的期望姿態在參數不定的情況下具有更高的精度與穩定性。

1 衛星模型的建立

1.1 衛星姿態運動學

由四元數描述的衛星姿態運動學方程為[19]：

將式(1)表示成矩陣形式為：

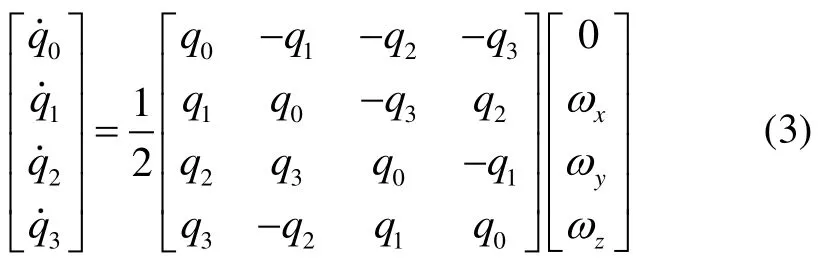
故得姿態運動學方程為：

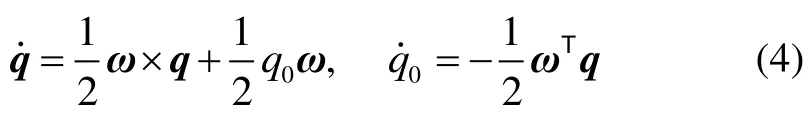
本文采用姿態誤差四元數作為姿態系統的控制量，設衛星姿態敏感器測量得到的姿態四元數為，目標姿態四元數為，則姿態誤差四元數為：

1.2 衛星姿態動力學

剛體衛星動力學方程如下[17,20]：

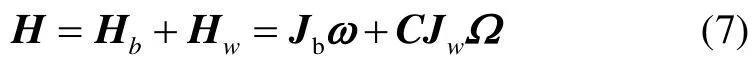
將式(7)代入式(6)得：

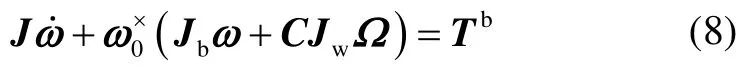
其中，

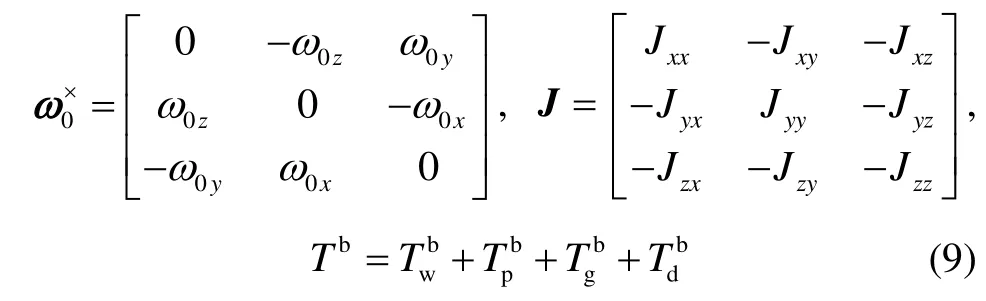
1.3 聯合執行模型

本文采用冷氣推力器和飛輪聯合作為微小衛星主動姿態穩定控制系統的執行機構，聯合控制結構圖如圖3所示。

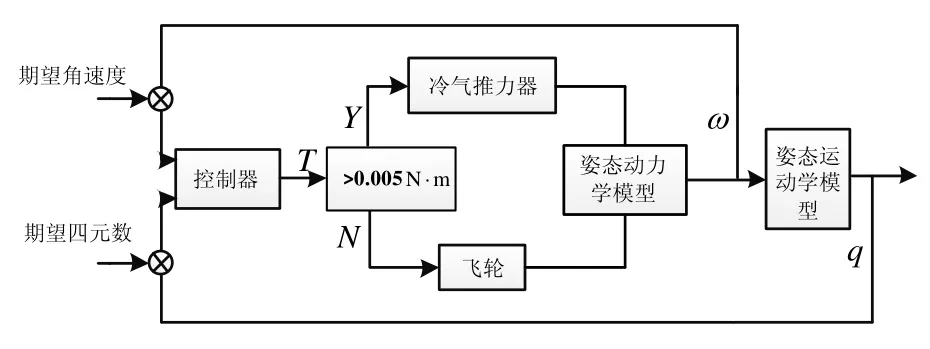
圖3 聯合控制結構圖Fig.3 Structure of joint control

本文研究的飛輪采用力矩模式，反作用飛輪在星體各軸角動量變化所產生的控制力矩可表示為：

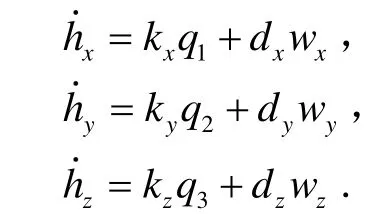
圖4表示一個典型的噴氣三軸穩定姿態控制系統[21]。

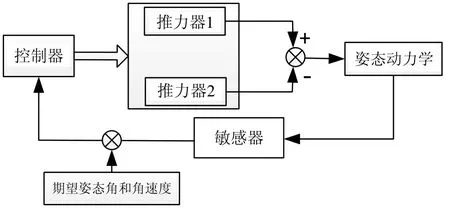
圖4 噴氣三軸姿態穩定控制系統Fig.4 Three-axis attitude stability control system of air injection

對裝有三軸噴嘴所產生的控制力矩為：

噴氣采用PWM控制，其結構如圖6所示。

圖6 噴氣推力器控制律結構圖Fig.6 Control law chart of jet thruster

噴嘴在一個控制周期內開啟時間為[17]：

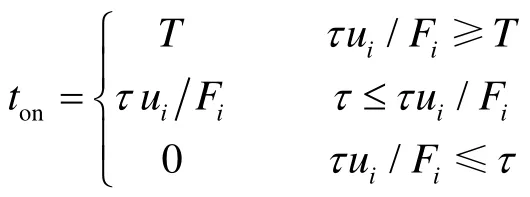
2 聯合執行機構控制律設計

2.1 基于歐拉軸轉動的遞階飽和PD控制律設計

在微小衛星大角度姿態機動過程中，必須考慮衛星執行機構最大輸出力矩，本文選擇冷氣推力器和飛輪作為微小衛星的執行機構，冷氣推力器最大輸出推力為，飛輪的推力選為。同時由于轉速陀螺測量精度限制，衛星的姿態旋轉角速度不能超過一定限度。在衛星姿態運動學模型和動力學模型的條件下，考慮衛星轉動慣量已知，且體旋轉角速度可測，得到如下形式的控制律：

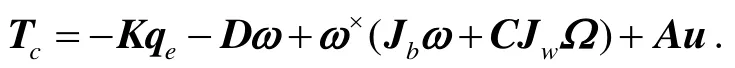
飛輪控制力矩的限制為：

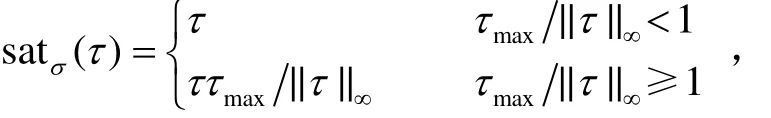
遞階飽和控制律可控制星體做繞歐拉軸的姿態機動，從而設計剛體衛星遞階飽和控制律為：

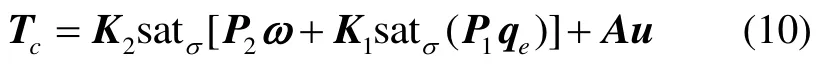
忽略陀螺效應耦合項，航天器角速度穿越零點的條件為：

2.2 基于歐拉軸轉動的遞階飽和模糊PD控制律設計

本節將模糊系統和基于歐拉軸轉動的遞階飽和PD控制方法相結合，設計出基于歐拉軸轉動的遞階飽和模糊PD姿態控制律，實現PD姿態控制律的比例增益和微分增益由模糊邏輯系統根據實時的姿態誤差在線整定。此控制方法具有模糊控制算法簡單、快速的特點，又具有傳統控制算法穩態控制精度高，有完整理論基礎的特點[23]。

在 2.1節的基礎上設計基于歐拉軸轉動遞階飽和模糊PD控制律，在設計的過程中，必須考慮衛星執行機構最大輸出的最大控制力矩，本文選擇冷氣推力器和飛輪作為微小衛星的執行機構。控制律為：

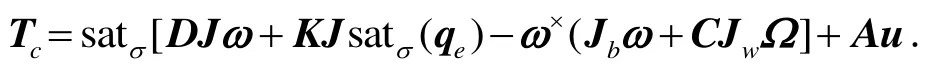
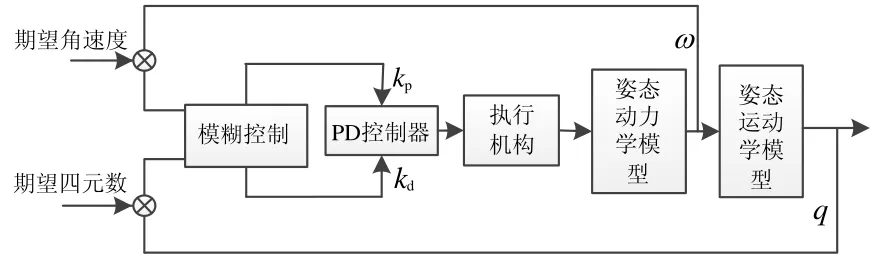
圖7 模糊PD控制律Fig.7 Fuzzy PD control law

圖7 中模糊控制器結構的設計是確定模糊控制器的輸入和輸出變量。本文選擇二維模糊控制器，模糊控制器的控制規則可表現為[24]：

{負大，負中，負小，零，正小，正大，正大}，其進一步表示為：

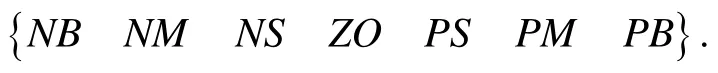
為提高本論文模糊控制的精度，將四元數誤差及四元數誤差的一階導數作為輸入量，在選擇描述其狀態的詞匯時，將零分為正零和負零，如下：

輸入詞集：

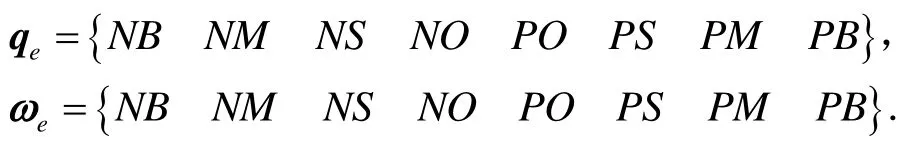
輸出詞集：

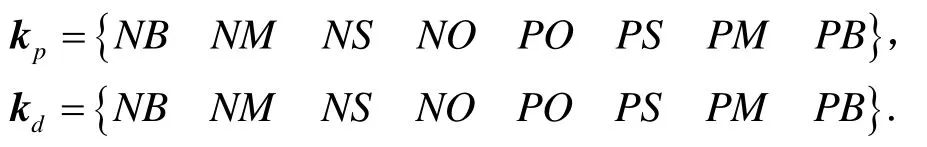
隸屬度函數如圖8~10所示。

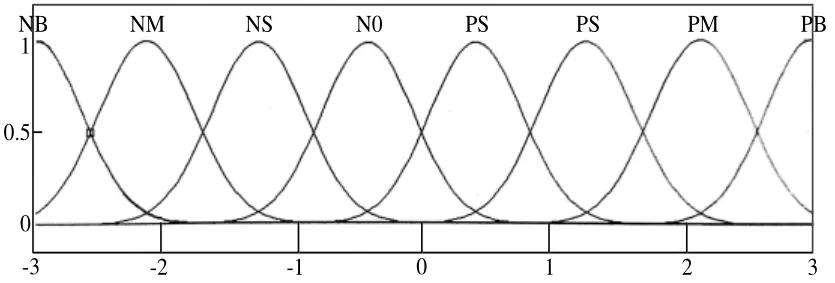
圖8 四元數誤差隸屬度函數Fig.8 Membership function of quaternion error

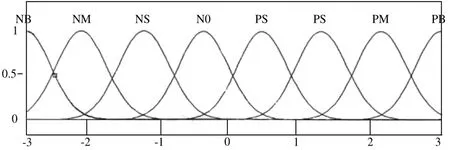
圖9 四元數誤差一階導隸屬度函數Fig.9 Membership function of quaternion error’s first-order derivative

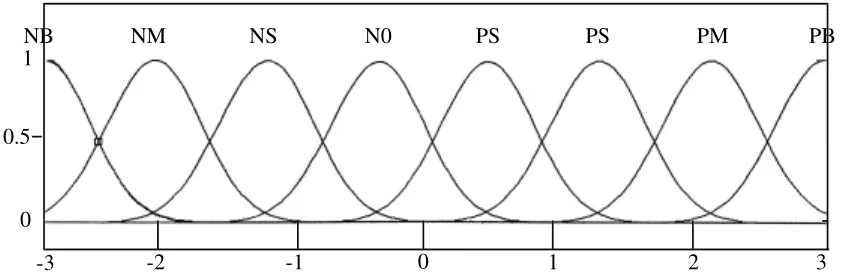
圖10 P、D參數隸屬度函數Fig.10 Membership function of P and D

本文采用的模糊規則表將四元數的誤差及四元數誤差一階導與PD參數一一對應，如表1和表2所示。

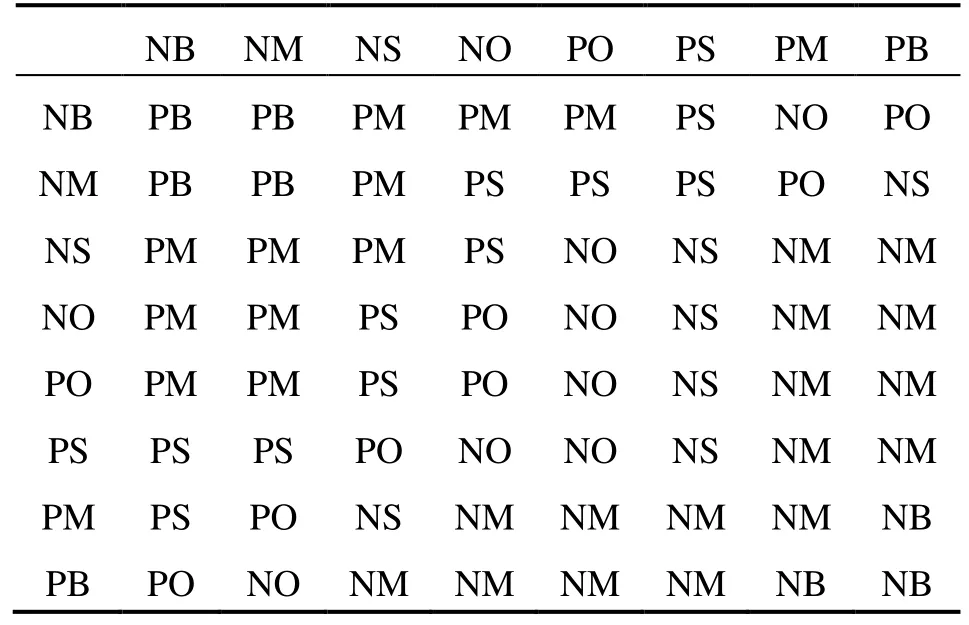
表1 Kp模糊規則表Tab.1 Kp Fuzzy control rule

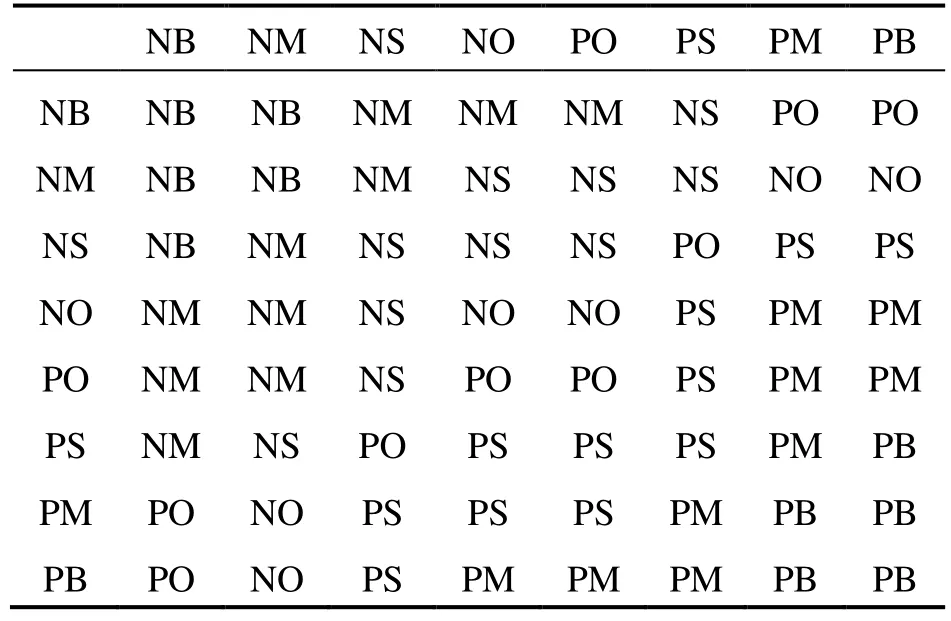
表2 Kd模糊規則表Tab.2 Kd Fuzzy control rule

3 仿真結果

3.1 PD控制律仿真結果及分析

由仿真結果可以看出，基于聯合執行結構的衛星姿態遞階飽和控制律控制衛星姿態機動需要耗時約150 s，在機動過程中飛輪輸出力矩限制在0.005 N?m內，冷氣推力器作為執行機構在0~4.5 s內提供大力矩，在力矩大于 0.005 N?m時采用冷氣推力器提供力矩。衛星繞軸機動，軸和軸飛輪的輸出力矩為零。衛星軸角速度限制在0.5 (°)/s內軸和軸飛輪的角速度為0°的情況。從仿真結果可以看出，姿態穩定后，姿態角誤差控制在 0.003°以內，另外采用反饋四元數誤差為參數的衛星姿態運動學方程可以保證衛星在大角度姿態機動時平滑經過姿態角為0°的情況，克服采用方向余弦描述姿態運動學時矩陣奇異的問題。衛星的姿態機動包含三個階段：

1）加速段0~20 s，星體轉速持續增加并在加速段結束達到允許最大值0.5 (°)/s；2）滑行段20~84 s，Z軸方向轉速保持最大值滑行；3）減速段84 s~，衛星姿態角速度重新回零，完成大角度姿態機動。

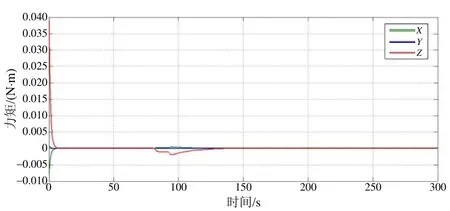
圖11 三軸力矩輸出曲線Fig.11 Three-axis torque output curve

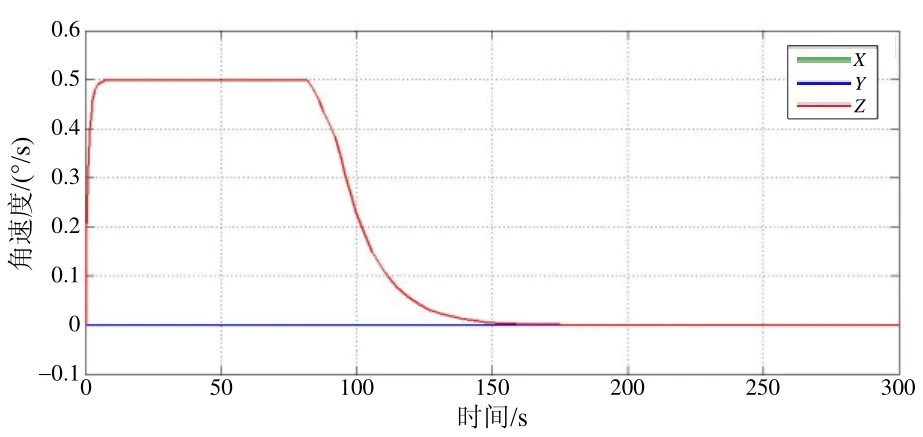
圖12 三軸角速度變化輸出曲線Fig.12 Three-axis angular velocity output curve

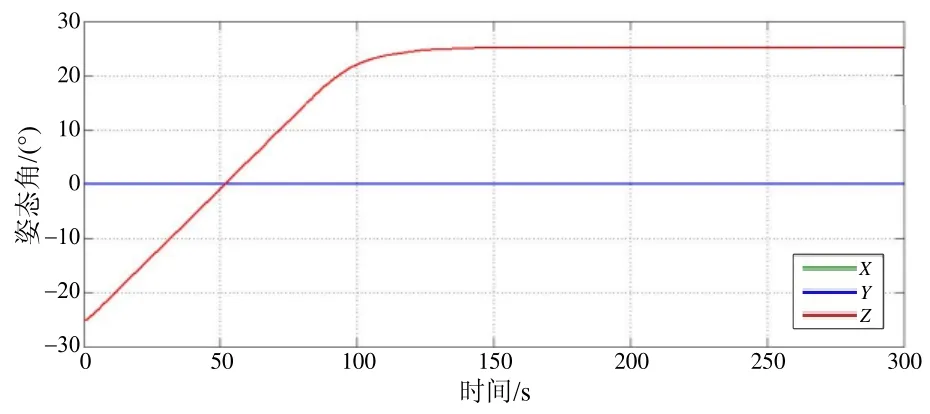
圖13 三軸角度變化輸出曲線Fig.13 Three-axis angle output curve

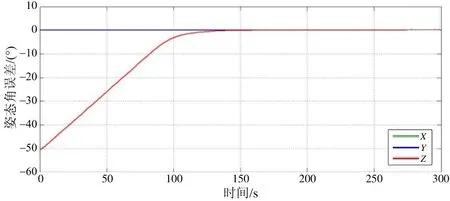
圖14 姿態角度誤差輸出曲線Fig.14 Attitude angle error output curve

3.2 模糊PD控制律仿真結果及分析

1）加速段 0~1.5 s，星體轉速持續增加并在加速段結束達到允許最大值0.5 (°)/s；

2）滑行段1.5~60 s，Z軸方向轉速保持最大值滑行；

3）減速段60 s~，衛星姿態角速度重新回零，完成大角度姿態機動。

PD姿態控制律的比例增益和微分增益由模糊邏輯系統根據實時的姿態誤差在線整定結果，如圖15~20所示。

圖15 在線整定Kp值輸出曲線Fig.15 Online setting Kp output curve

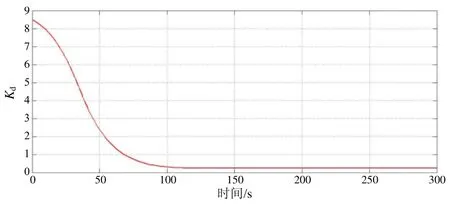
圖16 在線整定Kd值輸出曲線Fig.16 Online setting Kd output curve

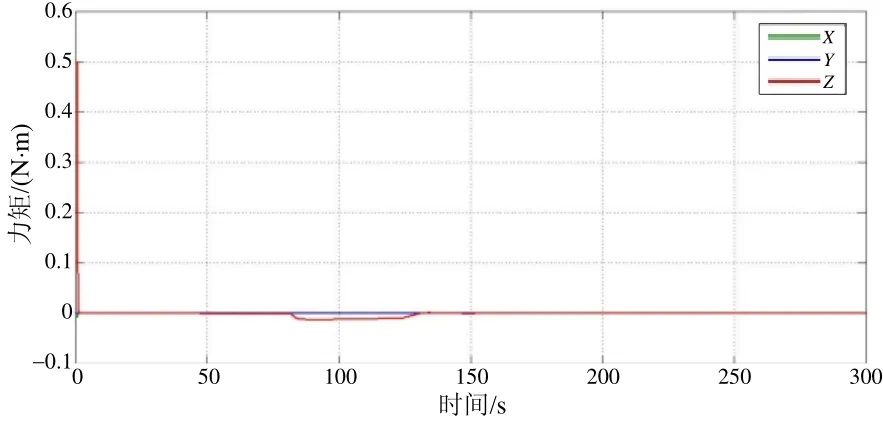
圖17 三軸力矩輸出曲線Fig.17 Three-axis torque output curve

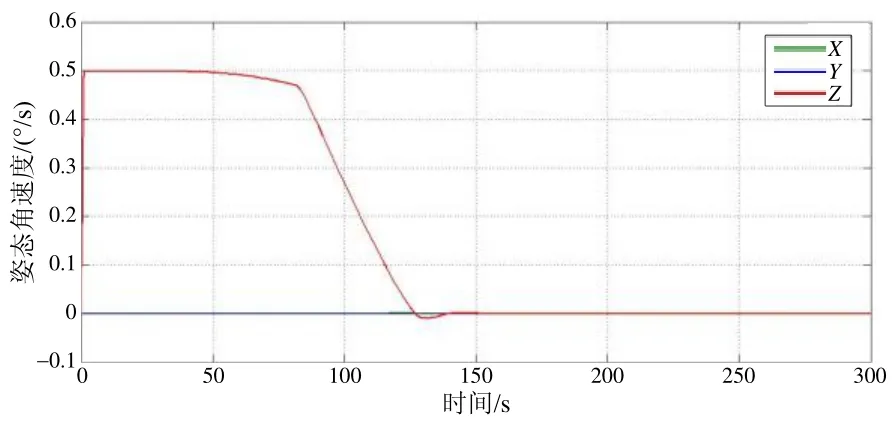
圖18 三軸角速度變化輸出曲線Fig.18 Three-axis angular velocity output curve

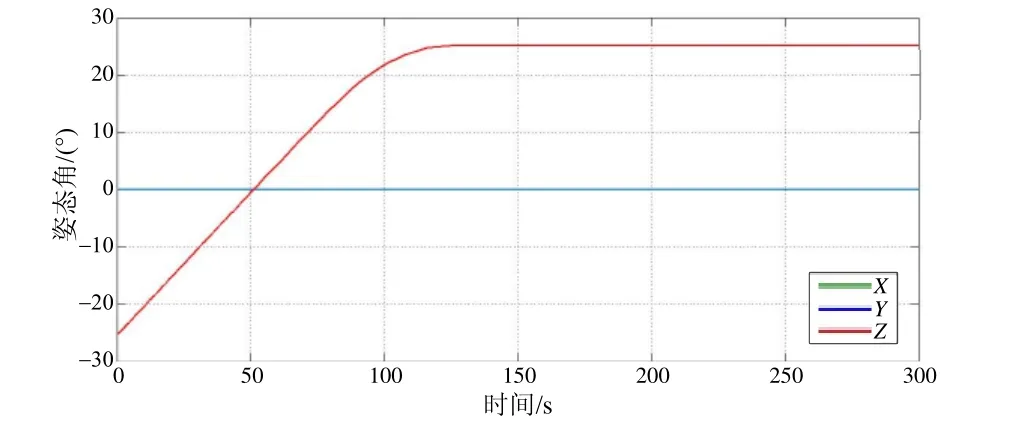
圖19 三軸角度變化輸出曲線Fig.19 Three-axis angle output curve

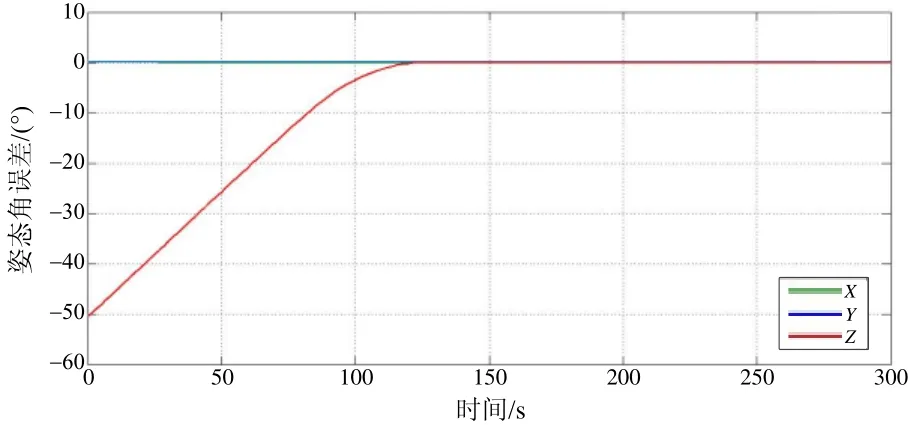
圖20 姿態角度誤差輸出曲線Fig.20 Attitude angle error output curve

進一步對PD和模糊PD進行比較分析，兩種控制律都采用基于遞階飽和的三軸穩定姿態控制算法，執行機構都采用冷氣推進器和飛輪聯合執行機構，比較結果見如表3所示。

表3 聯合執行機構控制算法比較Tab.3 Comparison on control algorithms of combination actuator

從表3可看出，模糊PD三軸穩定姿態控制律在系統穩定以及衛星機動的三個階段所用時間上略優于PD三軸穩定控制律，同時冷氣推力系統噴氣時間大大縮短，導致冷氣消耗也大大減小，適合于微小衛星的星載。

4 結 論

本文針對基于歐拉軸轉動的遞階飽和微小衛星聯合執行機構姿態控制，設計了PD和模糊PD兩種控制律控制噴氣/飛輪進行姿態大角度機動。聯合執行機構可以避免衛星在單獨采用飛輪控制時控制力矩頻繁的飽和卸載的情況。仿真表明，本文設計的模糊PD控制方法較PD控制方法縮短了收斂時間，節省噴氣燃料，同時具有較高的控制精度并且控制律設計簡便。綜合而言，模糊PD姿態控制算法既具有模糊控制算法簡單、快速的特點，又具有傳統PD控制算法穩態控制精度高，有完整理論基礎的特點，適合用于微小衛星的星載。

（

）：

[1] 葉東, 孫兆偉, 王劍穎. 敏捷衛星的聯合執行機構控制策略[J]. 航空學報, 2012, 33(6): 1108-1115.Ye D, Sun Z W, Wang J Y. Control strategy of hybrid actuator for agile satellites[J]. Acta Aoronautica et Astronautica Sinica, 2012, 33(6): 1108-1115.

[2] Wu S N, Sun X Y, Sun Z W, et al. Sliding-mode control for staring-mode spacecraft using a disturbance observer[J].Journal of Aerospace Engineering, 2010, 224(G2): 215-224.[3] Longbotham N, Bleiler C, ChaapelC. Spectral classification of WorldView2 multi-angle sequence[C]//IEEE GRSS and ISPRS Joint Urban Remote Sensing Event. 2011:109-112.

[4] 高樺, 鐘昊. 飛行器姿態大角度機動聯合控制物理仿真技術研究[J]. 計算機測量與控制, 2013, 18(10).2315-2317.Gao H, Zhong H. Physical simulation technology research for combined control of large angle maneuver of spacecraft[J]. Computer Measurement and Control, 2013,18(10): 2315-2317.

[5] 徐云, 朱欣華, 蘇巖. 一種基于坐標系級聯的攻角探測方法[J]. 中國慣性技術學報, 2016, 24(2): 196-201.Xu Y, Zhu X H, Su Y. Attack-angle detection method based on cascaded coordinate systems[J]. Journal of Chinese Inertial Technology, 2016, 24(2): 196-201.

[6] Chen X J, Steyn W H. Robust combined eigenaxis slew manoeuvre[C]//AIAA Guidance, Navigation, and Control Conference. 1999: 521-529.

[7] Liu Q, Wie B. Robust time-optimal control of uncertain flexible spacecraft[J]. Journal of Guidance Control and Dynamics, 1992, 15(3): 597-604.

[8] Wie B, Lu J B. Feedback control logic for spacecraft eigenaxis rotations under slew rate and control constraints[J]. Journal of Guidance Control and Dynamics, 1995,18(6): 1372-1379.

[9] Newman W S. Robust near time-optimal control[J]. IEEE Transactions on Automatic Control, 1990, 35(7): 841-844.

[10] Dodds S J, Vittek J. Spacecraft attitude control using an induction motor actuated reaction wheel with sensorless forced dynamic drive[C]//Proceedings of 1998 IEEE Colloquium on All Electric Aircraft. London, 1998: 1-14.

[11] 董朝陽, 華瑩, 陳宇. 空間飛行器大角度機動遞階飽和控制律設計[J]. 宇航學報, 2006, 27(5): 974-978.Dong C Y, Hua Y, Chen Y, et al. A cascade-saturation fuzzy variable structure control for spacecraft large angle attitude maneuvers[J]. Journal of Astronautics, 2006, 27(5):974-978.

[12] Hall C D, Tsiotras P, Shen H J. Tracking rigid body motion using thrusters and momentum wheels[J]. Journal of the Astronautical Sciences, 2002, 50(3): 311-323.

[13] Verbin D, Lappas V J. Rapid rotational maneuvering of rigid satellites with hybrid actuators configuration[J].Journal of Guidance Control and Dynamics, 2013, 36(2):532-547.

[14] Skelton C E, Hall C D. Mixed control moment gyro and momentum wheel attitude control strategies[J]. Astro dynamics, 2003, 116(1): 887-899.

[15] Hall C D, Tsiotras P, Shen H. Tracking rigid body motion using thrusters and momentum wheels[J]. The Journal of the Astronautical Sciences, 2002, 50(3): 311-323.

[16] Morten P T, Jan T G. Nonlinear attitude control of the micro satellite ESEO[C]//55th International Astronautical Congress. Vancouver, Canada, 2004: 1-12.

[17] 劉海穎, 王惠南, 陳志明, 等. 噴氣/偏置動量輪聯合微小衛星三軸穩定控制[J]. 系統仿真學報, 2010, 21(7):2023-2026.Liu H Y, Wang H N, Chen Z M, et al. Combined control for three-axis stabilization of micro-satellite using thrusters and single pitch bias momentum wheel[J]. Journal of System Simulation, 2010, 21(7): 2023-2026.

[18] Song G, Buck N V, Agrawal B N. Spacecraft vibration reduction using pulse-width pulse frequency modulated input shaper[J]. Journal of Guidance, Control and Dynamics, 1999, 22(4): 433-440.

[19] 鐘麗. 航天器姿態模糊 PD+姿態控制[D]. 北京: 北京理工大學, 2015.Zhong L. Research on fuzzy PD+ control algorithm for spacecraft attitude[D]. Beijing: Beijing Institute of Technology, 2015.

[20] 胡雅博. 姿態角速度受限的微小衛星姿態敏捷機動控制方法研究[D]. 南京: 南京航空航天大學, 2016.Hu Y B. Attitude agile maneuver control for micro- satellite with attitude angular velocity constraint[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2016.

[21] 張程. 飛輪控制小衛星大角度姿態機動控制[D]. 哈爾濱: 哈爾濱工業大學, 2012.Zhang C. The research on the control algorithms of large-angle maneuver of small wheel controlled satellite[D]. Harbin: Harbin Institute of Technology, 2012.

[22] Wie B, Weiss H, Arapostathis A. Quternion feedback regulator for spacecraft eigenaxis rotation[J]. Journal of Guidance, Control, and Dynamics, 1989, 12(3): 375-380.

[23] 秦鈺琦, 聞新. 衛星姿態模糊 PID 控制的可視化仿真分析[J]. 科技創新導報, 2015(29): 55-58.Qin Y Q, Wen X. The study of visualized simulation for satellite attitude based on fuzzy control[J]. Science and Technology Innovation Herald, 2015(29): 55-58.

[24] 李珮冉, 聞新, 陳桃. 航天器飛輪姿控系統模型的模糊控制方法設計[J]. 工業控制計算機, 2016, 29(9): 92-96.Li PR, Wen X, Chen T. Fuzzy control for spacecrafts attitude control system model based on momentum wheel[J]. Industrial Control Computer, 2016, 29(9). 92-96.