基于蒙特卡洛法的衛星分離姿態計算方法

康士朋，江 濤，耿盛韋，王金童

?

基于蒙特卡洛法的衛星分離姿態計算方法

康士朋1，江 濤1，耿盛韋2，王金童1

（1. 上海宇航系統工程研究所，上海，201109；2. 南京航空航天大學航空宇航學院，南京，201106）

為了計算以彈簧作為分離動力源的衛星在星箭分離時刻的分離姿態，建立了六自由度動力學方程，并采用龍格庫塔法求解了該方程，算例結果表明：通過該方法計算得到的分離角速度與ADAMS仿真計算結果相比，最大偏差小于0.77%。基于以上研究，針對衛星、彈簧裝置多個設計偏差對衛星分離姿態的影響，提出基于蒙特卡洛法的衛星分離姿態分析方法。飛行試驗結果表明，由該方法得到的分離角速度與常規保守算法相比，計算精度提高35%左右，解決了工程中由于采用將各個偏差取最大值進行保守計算而導致計算結果偏差較大的問題，可為衛星設計、彈簧裝置設計提供參考。

衛星；分離姿態；彈簧裝置；蒙特卡洛法；龍格庫塔法

0 引 言

隨著計算機技術、微納技術及微機電系統技術的迅速發展，質量在10~100 kg范圍的微納衛星以其研制周期短、低成本、高性能等優勢，在通信、軍事、遙感與對地測繪、空間科學試驗等領域表現出較好的發展前景[1]。

微納衛星通常以搭載或一箭多星的方式進行發射，以彈簧裝置作為分離動力源，以一定的分離速度、分離角速度與運載火箭進行分離[2]。衛星分離過程中，除了不能與火箭發生碰撞，還必須將分離角速度控制在允許范圍內，過大的分離角速度甚至會導致衛星無法控制姿態，直接影響飛行任務成敗。

衛星分離姿態計算方法主要包括兩種：數值計算方法和基于ADAMS軟件的仿真計算方法。

數值計算方法包括兩種：a）建立常質量航天器動力學方程，并采用龍格庫塔方法進行數值求解，如：付碧紅[3]、盧麗穎[4]分別以搭載星、子星為研究對象，建立并求解了三自由度動力學方程，Jeyakumar，BN Rao[5]也通過龍格庫塔法得到了分離體的非線性常微分方程數值解；b）建立拉格朗日動力學方程，如：王鑫等[6]采用拉格朗日動力學原理建立了分離體姿態動力學模型，探索了分離體姿態動力學方程組數值求解方法。而隨著計算機仿真技術的發展，眾多學者[7~11]提出了采用ADAMS軟件進行了衛星分離仿真分析，ADAMS軟件基于多剛體動力學方程，采用自動變階、變步長方法進行計算[12]。

但相比上述計算模型，實際情況中存在兩類偏差：一類是衛星重量偏差、質心偏差及轉動慣量偏差；另一類是彈簧裝置推力偏斜、推力大小偏差及安裝誤差。這些偏差因素都將影響衛星的分離姿態。

在工程應用中，為考慮以上偏差因素對分離姿態的影響，通常采用的方法是將每一個偏差量都取到最大，計算極限的分離姿態。然而，用所有偏差因素的極限值計算得到的極限分離姿態產生概率非常小，遠遠超出了航天可靠性要求。因此，使用以上方法計算結果偏于保守。

使用以上保守的計算方法時，為了滿足衛星分離指標要求，通常采取兩種措施：一種是減小以上因素的設計偏差值；另一種是提高彈簧裝置生產精度，并大量投產，選配出彈簧推力偏差較小的彈簧裝置。以上方法在限制了衛星與彈簧裝置結構設計的同時也提高了產品生產成本。

因此，本文以采用彈簧裝置進行分離的微納衛星為例，從概率分布的角度，提出基于蒙特卡洛法的考慮設計偏差影響的衛星分離姿態計算方法，并通過飛行試驗驗證了該方法的有效性。

1 動力學方程建立與求解

1.1 建立動力學方程

以CZ-4B運載火箭搭載發射微納衛星（X衛星）為例，建立六自由度常質量航天器動力學方程。該衛星在4個彈簧裝置作用下與運載火箭進行分離，分離方案如圖1所示。

圖1 衛星分離方案

由于衛星質量、轉動慣量遠遠小于運載火箭末子級質量、轉動慣量，因此分離過程中，不考慮運載火箭對衛星分離姿態的影響。

將坐標系設定于星箭分離面中心，固定在運載火箭上，以圖1模型分離系統為研究對象，建立4個彈簧裝置作用下的分離姿態計算分析模型，如圖2所示。

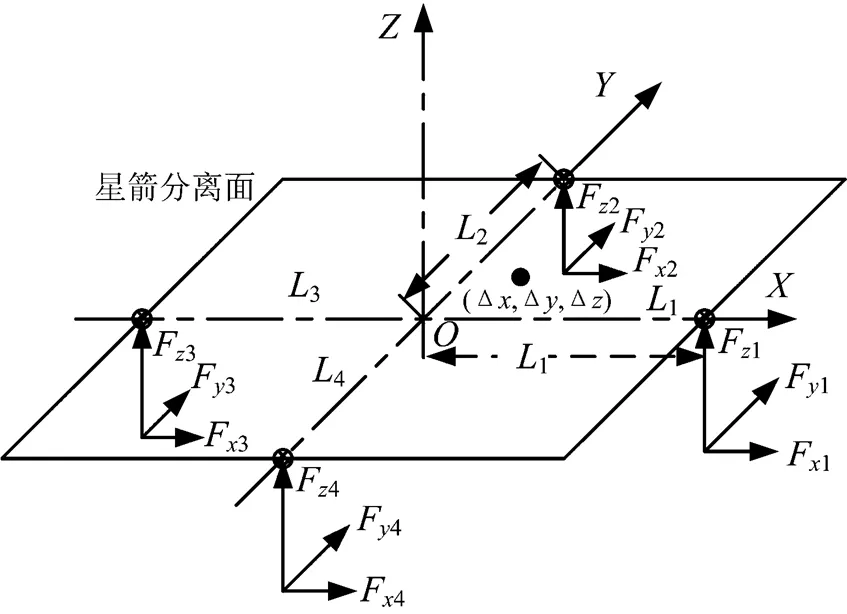
圖2 分離姿態計算模型

Δ，Δ，Δ—衛星質心在，，軸的偏移量；1，2，3，4—考慮安裝偏差后的4個彈簧的安裝距離，其中3，4為負值；F第個彈簧裝置推力在向分力（=1,2,3,4）；F第個彈簧裝置推力在向分力；F第個彈簧裝置推力在向分力

考慮彈簧推力偏斜影響，以單個彈簧為研究對象，根據總體坐標系，將每一個彈簧裝置的推力進行分解，如圖3所示。

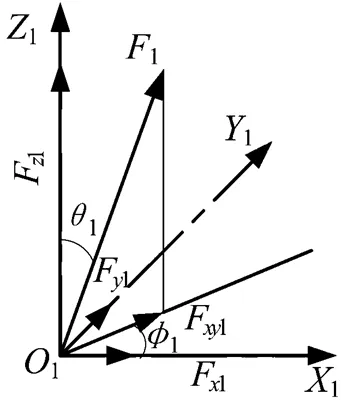
圖3 彈簧推力分解示意

F—第個彈簧裝置推力；—第個彈簧推力與軸夾角；—第個彈簧力在平面投影力與軸夾角

根據圖3可以得到每個彈簧推力在坐標方向的分解力為

根據圖2和式（1）可以得到使衛星繞三軸旋轉力矩M，M，M的計算公式為

根據牛頓第二定律和動量矩定理，建立衛星與運載火箭末子級兩個剛體之間的六自由度動力學方程：

1.2 動力學方程求解

上述方程維數高、變量多、且互相耦合，無法求解其解析解，可采用龍格庫塔方法進行數值計算求解。

在計算過程中，彈簧推力、力矩為變化值，為了解決這一問題，本文提出將彈簧工作時間劃分為多個連續子區間，在每一個子區間內，將該區間中間時刻的彈簧力作為該子區間內的彈簧推力。

首先計算彈簧裝置工作時間，以4個彈簧組成的分離系統為研究對象，由于彈簧質量遠小于衛星質量，衛星運動為彈簧振子簡諧運動。

在初始時刻0=0，初始速度為0，彈簧變形量達到最大值max，max即為彈簧振子振幅；在彈簧工作結束時刻s，彈簧變形量降低至最小值min：

式中為分離系統簡諧運動角頻率。

根據以上公式計算彈簧工作時間為

式中k為第個彈簧的剛度。

式中為第個彈簧力角頻率；為彈簧效率，根據工程經驗取值。

本文基于MATLAB軟件，采用龍格庫塔數值計算方法來求解公式，求解過程如圖4所示。

圖4 動力學方程求解流程

1.3 計算方法驗證

為了驗證本文計算方法的正確性，針對同一組計算參數，采用該方法和ADAMS仿真計算兩種方法進行計算，并將計算結果進行比對。

參照X衛星給出一組設計參數，如表1所示，進行衛星分離姿態計算。

表1 計算參數匯總

續表1

4#彈簧力/NFmax=250；Fmin=80 1#彈簧位置/mm107.05 2#彈簧位置/mm107.08 3#彈簧位置/mm106.99 4#彈簧位置/mm107.0 1#彈簧推力角度/(°)θ1=0.762；φ1=30 2#彈簧推力角度/(°)θ2=0.742；φ2=45 3#彈簧推力角度/(°)θ3=0.758；φ3=60 4#彈簧推力角度/(°)θ4=0.750；φ4=90 彈簧效率η0.85

注：max—彈簧裝置最大推力；min—彈簧裝置最小推力

根據式（1）計算得到彈簧工作時間為0.074 2 s，再將該時間劃分為50份，根據1.2節公式，采用MATLAB軟件對衛星分離姿態進行計算，計算結果以分離角速度為例，如圖5和表2所示。

圖5 數值計算結果

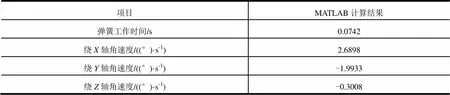
表2 數值計算結果匯總

在ADAMS軟件中，建立仿真分析模型，衛星的質量、慣量和質心位置同表1。在地面建立總坐標系，在彈簧推力作用點施加彈簧推力，該采用行程與剛度函數表示。

設置計算時間為0.1 s、載荷步數量為50，進行計算，結果如圖6、表3所示。

圖6 ADAMS姿態角速度結果

表3 仿真計算結果匯總

將由兩種方法得到的計算結果進行對比，得到兩種方法相對差如表4所示。

表4 計算偏差匯總

經過表4對比可得，兩種計算方法得到的計算結果最大相對差為0.77%，這是由于將子區間中間時刻彈簧推力簡化為該子區間彈簧推力而造成的。本算例證明了1.2節計算方法的正確性。

2 考慮設計偏差的分離姿態計算方法

2.1 計算方法

蒙特卡洛方法不同于確定性的數值方法，它是通過模擬隨機變量來解決數學問題的非確定性的（概率統計的或隨機的）數值方法[13]。

因此，本文提出基于蒙特卡洛方法的衛星分離姿態評估方法：首先根據各個設計變量的偏差范圍隨機產生大量的設計參數；再根據第1節方法進行衛星分離姿態計算，將得到大量衛星分離姿態計算結果；再對這些計算結果進行統計，得到其分布規律；最后根據概率分布范圍，找出合理的極限分離姿態。分析方法流程如圖7所示。

圖7 衛星分離姿態分析方法

2.2 計算方法驗證

以CZ-4B運載火箭搭載發射X衛星為例，驗證該方法有效性。

衛星、彈簧裝置完成生產后，對衛星的質量、質心位置、轉動慣量進行實測；對彈簧裝置的推力大小、安裝位置進行實測，如表5所示。

表5 產品實測參數

由于彈簧裝置在設計過程中為防止彈簧推桿與彈簧殼體發生卡滯，兩者之間為間隙配合，因此彈簧推力是在一定角度范圍偏斜。根據彈簧推桿、彈簧殼體的加工參數，計算得到彈簧最大推力偏斜為0.622°。

針對這一項設計偏差，將采用傳統保守算法以及第2.1節提出的算法對X衛星的分離姿態進行計算，并將兩種方法的計算結果與飛行試驗結果進行對比。

按照保守算法，將推力偏斜設置為最大值，確定衛星分離最嚴酷工況，如表6所示。

表6 保守算法計算參數

根據表5、表6的設計參數，在ADAMS軟件中進行衛星分離姿態仿真分析，建模方法同1.3節，以分離角速度為例，計算結果為：2.892 (°)/s，-3.0 (°)/s，0.970 (°)/s。

根據2.1節提出的評估方法，設置彈簧推力偏斜角度為：∈[0,0.622°]，∈[0,360°]，在MATLAB計算程序中產生100 000個隨機變量，通過計算得到100 000組計算結果，以分離角速度為例，對這些計算結果進行處理，通過程序判斷計算結果服從正態分布規律，如圖8至圖10所示，并得到繞三軸分離角速度均值與方差，如表7所示。

圖8 繞X軸分離角速度分析結果

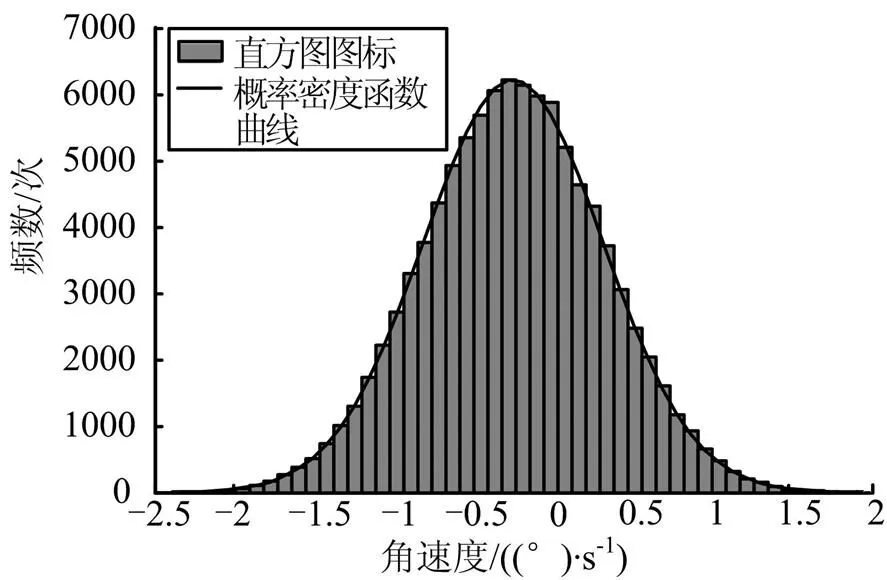
圖9 繞Y軸分離角速度分析結果

圖10 繞Z軸分離角速度分析結果

表7 分離角速度均值與方差

據表7結果，按照3原則，得到置信度為99.73%的衛星繞三軸分離角速度：1.822 (°)/s，-1.940 (°)/s，0.594 (°)/s。

2014年，該衛星通過CZ-4B運載火箭搭載發射成功，根據衛星回傳數據，星箭分離時刻，衛星繞三軸分離角速度分別為：0.8 (°)/s，-0.6 (°)/s，0.17 (°)/s。

對以上數據進行匯總，如表8所示。

表8 計算、試驗結果數據匯總

對比表8數據可得，由第2.1節方法得到的計算結果與常規保守法計算結果相比，計算精度分別提高37%，35%，39%，該方法可以代替傳統的保守算法。

綜合表7和飛行結果，如果按照1σ原則，得到置信度為68.27%的分析結果，0.7 (°)/s、-0.806 (°)/s、0.198 (°)/s，不能包絡飛行試驗結果；如果按照2σ原則，得到置信度為95.45%的分析結果，1.261 (°)/s、-1.373 (°)/s、0.396 (°)/s，可以包絡飛行試驗結果；說明至少按照2σ原則給出的計算結果才可以滿足使用要求，因此本文按照3σ原則給出的計算結果。

3 結 論

本文建立了考慮推力偏斜的六自由度動力學方程，采用龍格庫塔方法求解該方程，算例結果表明，由該方法得到的分離角速度結果與仿真計算結果比最大相差為0.77%，驗證了該方法正確性。

基于以上研究，提出基于蒙特卡洛法的考慮設計偏差影響的衛星分離姿態計算方法。算例結果表明，衛星分離角速度計算結果服從正態分布規律。飛行試驗結果表明，要至少按照2σ原則給出的計算結果才可以滿足使用要求，按照本文提出的3σ原則給出的計算結果與常規保守算法相比其計算精度提高35%左右。

該方法解決了工程中由于采用將各個偏差取最大值進行計算而導致計算結果偏差較大的問題,該方法可為衛星設計、彈簧裝置設計提供參考。

[1] 石榮, 李瀟, 鄧科. 微納衛星發展現狀及在光學成像偵察中的應用[J]. 航天電子對抗, 2016: 32(1): 8-13.

[2] Liu L K, Zheng G T. Parameter analysis of PAF for whole-spacecraft vibration isolation[J]. Aerospace Science and Technology, 2007(11): 464-472.

[3] 付碧紅, 杜光華. 搭載星與運載火箭分離的動力學研究[J]. 飛行力學, 2006, 24(1): 55-58.

[4] 盧麗穎, 孟憲紅, 邢依琳. 衛星空間分離動力學研究[J]. 動力學與控制學報，2014, 12(2): 165-169.

[5] Jeyakumar D, Rao B N. Dynamics of satellite separation system[J]. Journal of Sound and Vibration, 2006, 297(1-2): 444-455.

[6] 王鑫, 袁曉光, 楊星. 基于拉格朗日方法的飛行器多體分離姿態動力學分析研究[J]. 西北工業大學學報: 2014, 32(1): 18-22.

[7] 王秋梅, 孟憲紅, 楊慶成. 衛星二次分離方案仿真研究[J]. 系統仿真學報, 2010, 22(9): 2217-2222.

[8] 沈曉鳳, 肖余之, 杜三虎, 等. 基于蒙特卡羅方法的小衛星偏心分離動力學分析[J]. 上海航天, 2014, 31(1): 12-17.

[9] 沈曉鳳, 肖余之, 康志宇. 小衛星偏心分離動力學仿真模型的建立與驗證[J]. 飛行力學, 2012, 30(3): 258-262.

[10] 曾文花, 吳琳娜. 多星與上面級非對稱分離技術研究[J]. 上海航天, 2014, 31(2): 30-36.

[11] 張兵, 岑拯. 多星分離的ADAMS仿真[J]. 導彈與航天運載技術, 2004(2): 1-6.

[12] 胡星志. 小衛星星箭分離系統設計、分析與優化研究[D]. 長沙: 國防科技大學, 2012.

[13] 金暢. 蒙特卡洛方法中隨機數發生器和隨機抽樣方法的研究[D]. 大連: 大連理工大學, 2005.

Calculation Method of Satellite Separation Attitude Based on Monte Carlo Method

Kang Shi-peng1, Jiang Tao1, Geng Sheng-wei2, Wang Jin-tong1

(1. Aerospace System Engineering Shanghai, Shanghai, 201109; 2. College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing, 201106）

In order to calculate the separation attitude of the satellite which is separated by spring device, the 6 degrees of freedom dynamic equation is established and solved by the Runge-Kutta Method. The numerical examples indicate that the maximum deviation of separation angular velocity obtained by this method and the ADAMS simulation is less than 0.77%. Based on the above studies, a analysis method based on Monte Carlo Method is proposed to calculate satellite separation attitude considering the satellite and spring device design deviations. The results of flight test indicate that the proposed method can improve the accuracy by 35% compared with the conventional conservative algorithm. The method solves the problem that the deviation of the calculation result is large due to the conservative calculation of the maximum value of each deviation. This method can provide a reference for satellite design and spring device design.

Satellite; Separation attitude; Spring device; Monte Carlo method; Runge-Kutta method

1004-7182(2017)06-0036-06

10.7654/j.issn.1004-7182.20170609

V412.4+2

A

2017-06-04；

2017-07-11

康士朋（1983-），男，博士研究生，工程師，主要研究方向為箭體結構和星箭連接分離裝置設計