應用題考查熱點

殷高榮

數學應用題指利用數學知識解決其他領域中的問題，高考對應用題的考查已經逐步成熟，特別是新課程標準出來之后，對應用問題考查的力度正在加大，考試注重分析問題及方法的新穎性，提高了對同學們適應陌生情境的能力的考查.對于一些函數的應用問題，同學們往往感覺無從下手，十分困難.高考數學應用題的命題背景常常關注一些與函數導數、平面圖形、數列、空間圖形、概率統計等相關的問題.

一、以立體幾何為背景的應用題

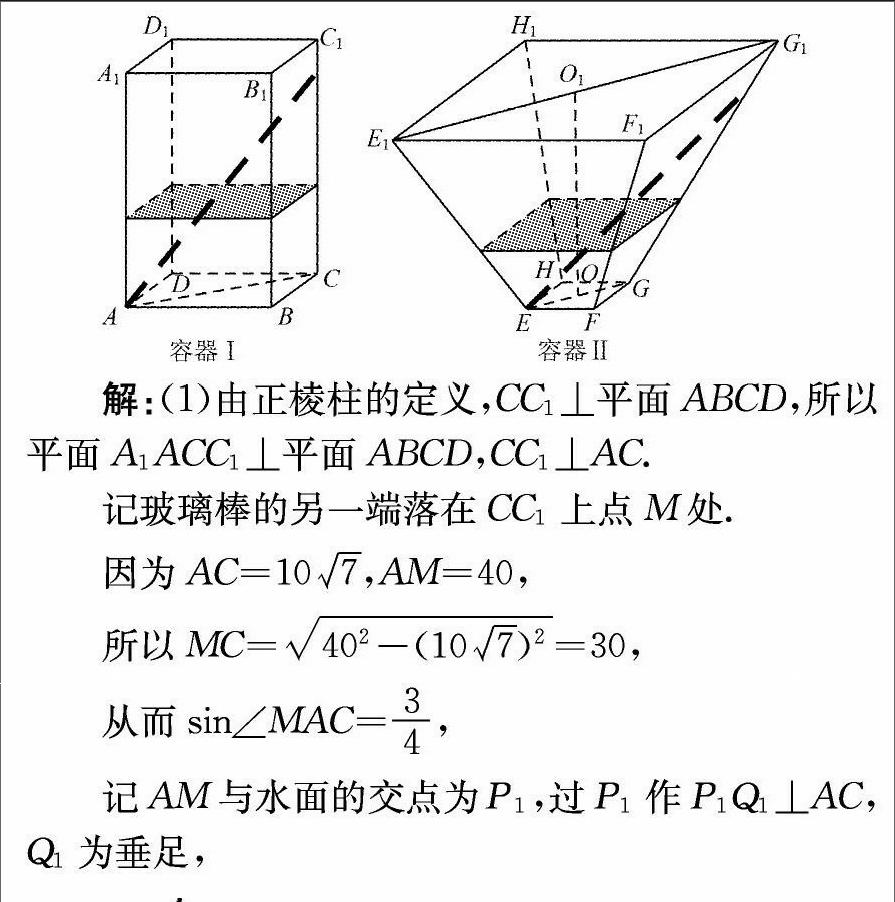
例1 如圖，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱臺形玻璃容器Ⅱ的高均為32cm，容器Ⅰ的底面對角線AC的長為107cm，容器Ⅱ的兩底面對角線EG，E1G1的長分別為14cm和62cm.分別在容器Ⅰ和容器Ⅱ中注入水，水深均為12cm.現有一根玻璃棒l，其長度為40cm.（容器厚度、玻璃棒粗細均忽略不計）

（1）將l放在容器Ⅰ中，l的一端置于點A處，另一端置于側棱CC1上，求l沒入水中部分的長度；

（2）將l放在容器Ⅱ中，l的一端置于點E處，另一端置于側棱GG1上，求l沒入水中部分的長度.

應用題的信息量大，重點考查同學們處理問題的能力.在解應用題時通常有以下步驟：首先是審題：理解文字表達的題意，分清條件和結論，理順數量關系，這一關是基礎；接著是建模：將文字語言轉化為數學語言，利用數學知識，建立相應的數學模型，熟悉基本數學模型，正確進行建“模”是關鍵的一關；然后求模：求解數學模型，得到數學結論，一要充分注意數學模型中元素的實際意義，更要注意巧思妙作，優化過程；……