基于簡化描述符的仿射不變圖像匹配算法

李記鵬，尹顏朋

（四川大學計算機學院，成都 610065）

0 引言

圖像匹配是計算機視覺的一個重要分支，廣泛應用于三維重建、目標識別、圖像檢索等領域。基于特征的匹配方法由于計算量少、速度快得到了研究者的青睞，近年來大量的局部特征檢測子涌現出來，這些檢測子都具有平移不變性，Harris檢測子[11]對于旋轉也具有不變性，Harris-Laplace,Hessian-Laplace以及高斯差分區域檢測子具有尺度不變性[12-15]，其他一些區域檢測子如 Harris-affine,Hessian-affine,MSER（Maximally Sta?ble Extremal Region）對于圖像的仿射變換具有一定的適應性[16,13,5]。Lowe提出的特征檢測方法將SIFT（Scale Invariant Feature Transform）檢測子與SIFT描述符相結合，具有尺度、平移、旋轉不變性，對光照、幾何變換有一定的適應性。相關文獻表明相對于其他描述符而言，SIFT描述符性能更加穩定[17]，因此被廣泛應用于圖像匹配，然而SIFT特征描述符維度過高，匹配圖像的時間開銷很大而且不具備仿射不變性。YanKe等提出PCA（Principal Components Analysis）-SIFT[2]方法有效的降低了描述符的維度，提高了圖像匹配的速度，但是該方法的降維操作時間復雜度過高。ZhipingZhou等提出的 MDS（Multidimensional Scaling）-SIFT[3]方法在一定程度上克服了該問題，同時引入局部紋理特征約束提高了匹配的精度。XinminZhou[4]提出一種方法使用圓形區域替代正方形區域，然后計算每個子區域梯度方向分布，該方法極大的簡化了描述符生成的過程，提高了匹配速度。上述方法雖然提高了圖像匹配的效率，但是都不具備仿射不變性。J.Matas[5]等提出一種適用于寬基線圖像匹配的方法，提取圖像的MSER特征進行圖像匹配，WenchaoHu等將MSER特征與SIFT特征相結合提出一種對于仿射形變具有較好魯棒性的匹配算法[6]，但是這些方法依然不具有完全仿射不變的特性。J.M.Morel等將攝像機的成像過程近似為仿射變換，通過模擬攝像機位置變化產生的仿射形變提出一種完全仿射不變的圖像匹配算法即ASIFT（Affine-SIFT）[7]，然而該算法時間開銷太大。

本文將簡化描述符與ASIFT的模擬方法相結合提出一種完全仿射不變的匹配算法，實驗證明該方法對于仿射形變較大的圖像具有較好的魯棒性，匹配速度明顯優于ASIFT。

1 基于簡化描述符的仿射不變匹配算法

1.1 基于圓形鄰域的簡化描述符

SIFT生成描述符時，為了保證旋轉不變性在統計梯度方向之前需要將整個采樣區域旋轉至主方向，由于SIFT采樣區域為方形區域旋轉前后無法完全重疊，尤其是角落區域的像素點旋轉后大部分均不在重疊區域如圖1（a）所示，因此采用相同尺寸的方形區域生成描述符肯定會產生很大的誤差。在實踐中相關算法為了克服該誤差往往采用更大的方形區域生成描述符，這種做法不可避免的帶來了了冗余的像素旋轉操作，增加了運行時間。圓形區域則不相同，對于旋轉操作具有更好的不變性，旋轉前后覆蓋的像素完全一致如圖 1（b）所示。

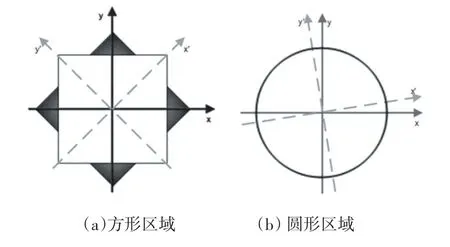
圖1 方形區域和圓形區域比較

因此本文提出一種在圓形鄰域內使用扇形區域生成描述符的方法，具體過程如下：

（1）使用SIFT方法在尺度空間中尋找圖像的關鍵點，同時確定主方向。

（2）在相應的尺度空間中以關鍵點為中心產生一個圓形區域，計算像素梯度，將圓形區域旋轉至主方向，對梯度做高斯加權。

（3）將圓形區域分為2×2個扇形子區域，在每個扇形區域內統計8個方向的梯度直方圖如圖2（b）所示。

（4）將4個扇形的梯度直方圖合并得到32維的描述符然后進行歸一化處理，以降低光照變化對描述符的影響。

SIFT生成描述符時以關鍵點為中心生成一個方形鄰域，然后將其分為16個子區域，在每個在區域內統計8個方向的梯度直方圖如圖2（a）所示，最終生成128維描述符。盡管本文方法也需要統計梯度直方圖，但是只需要在4個扇形區域上統計，統計次數比SIFT少了12次，另外本文算法的描述符維度降低了64維，在進行描述符相似度的計算時，使用該描述符可以大大降低計算量，提高匹配效率。

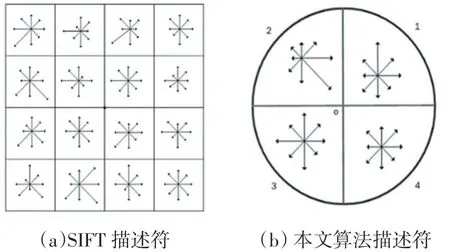
圖2 描述符對比

1.2 仿射不變匹配算法

降維后的描述符與SIFT描述符一樣具有尺度，旋轉不變性并且對于光照、強度變化有一定的適應性，而且匹配速度有一定提高，然而仍然不具有仿射不變性。本文受ASIFT模擬思想的啟發，通過模擬攝像機位置變化產生的形變克服這一缺陷，提出一種完全仿射不變的匹配算法。

在仿射相機模型中，攝像機成像過程被簡化為一個仿射變換，該仿射變換存在唯一的SVD分解：

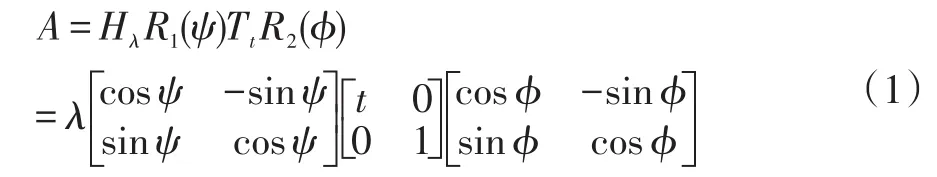
其中λ>0 λ>0,λt是A的行列式，Ri表示旋轉，與相應的對角矩陣表示傾斜因子。該分解的幾何解釋如圖3所示，u表示扁平的物體平面，右上方的平行四邊形表示攝像機平面，θ，?分別是攝像機的緯度經度，用來表示攝像機的位置，ψ表示攝像機平面的旋轉，λ表示放縮倍數，其中θ與公式1中的t t一一對應，t=1/cosθ表示圖像的絕對傾斜。

假設u1=u(A(x,y))u1=u(A(x,y)),u2=u(B(x,y))u2=u(B(x,y))表示攝像機在不同視角下得到的兩幅圖像，其中A,B表示成像過程中的仿射變換，使用公式1可以定義u1到u2的變換如下：

其中τ與兩幅圖像的絕對傾斜、經度差有關，表示圖像之間的相對傾斜，該定義的詳細信息請參閱文獻[7]。J.M.Morel在該理論的基礎上對每一幅圖像做仿射變換模擬攝像機位置變化產生的仿射形變提出一種完全仿射不變的匹配算法即ASIFT。本文將簡化描述符與ASIFT模擬機制相結合在保證仿射不變的前提下，提高匹配效率，算法具體過程如下：

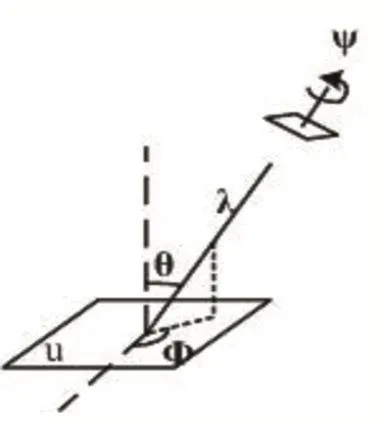
圖3 SVD分解的幾何解釋

（1）對每一幅圖像進行仿射變換模擬由于攝像機位置變化產生的仿射形變。圖像的仿射形變主要取決于經緯度的變化，因此在對原始圖像做仿射變換時只對攝像機的經緯度進行模擬，為了模擬出盡可能多的形變圖像，在對經緯度采樣時按照如下規則進行：

a.對緯度采樣時保證與之相關的傾斜因子t按照1,a，a2，…，an的規律變化，其中

b.對經度采樣時?按照0,b/t，…，kb/t的規律變化，其中b=72°，k是kb/t<=180°的最大整數解。

（2）對每一幅模擬圖像使用SIFT方法檢測特征點，確定主方向，最后使用圓形區域生成簡化的32維描述符。

（3）對左右圖像的任意一對模擬圖像使用最近距離次近距離比算法建立匹配關系如圖4所示。最近距離次近距離比算法匹配圖像時，計算左圖中每個描述符與右圖中所有描述符的歐氏距離，如果最近距離和次近距離的比值小于給定的閾值，則兩個描述符對應的點匹配成功。最終的匹配結果是所有模擬圖像對匹配結果的并集，由于模擬圖像模擬了攝像機位置變化產生的各種仿射形變，因此該匹配結果對于圖像的仿射變換具有較好的適應性，文獻[7]在理論上證明了該方法的仿射不變性。

（4）使用對極幾何的約束消除錯誤匹配，RANSAC（Random Sample Consensus）[8]是剔除錯配點常用的方法，然而該方法對于初始匹配點集的依賴性較大，如果初始匹配點集中錯誤匹配點過多，將無法正確的剔除錯配點，ORSA（Optimized RANSAC）[9]是基于 RANSAC改進而來的方法，該方法有效的克服了RANSAC對于初始匹配點集過分依賴的缺陷，本文使用該方法消除錯匹配得到最終的匹配結果。

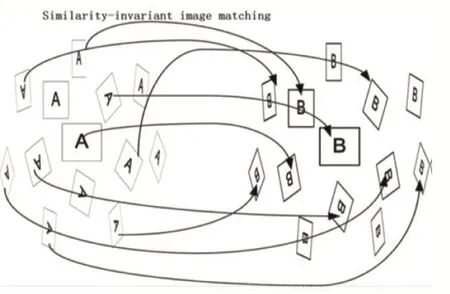
圖4 仿射不變匹配算法

2 實驗結果與分析

研究人員在ASIFT源代碼的基礎上對本文算法進行編程實現，為了評價匹配性能，采用Morel圖像集[7]對本文算法進行測試，并與ASIFT的匹配性能進行對比。Morel圖像集分為絕對傾斜測試集和相對傾斜測試集兩部分，絕對傾斜測試集包括一幅油畫在放縮倍數為1和10的情況下拍攝的兩組圖像，以及一本雜志在放縮倍數為4的情況下拍攝的一組圖像，相對傾斜測試集包含一本雜志在絕對傾斜為2和4的情況下攝像機經度從零度到九十度逐漸增大拍攝得到的兩組圖像。

2.1 絕對傾斜實驗分析

本文使用放縮倍數為1的圖像集進行絕對傾斜實驗，將本文方法與ASIFT在匹配點數、匹配速度兩個方面對比，實驗結果如表1所示，表中各列從左至右一次表示絕對傾斜值得大小，ASIFT匹配點數，本文算法匹配點數，ASIFT匹配速度，本文算法匹配速度，其中匹配速度計算公式如下：

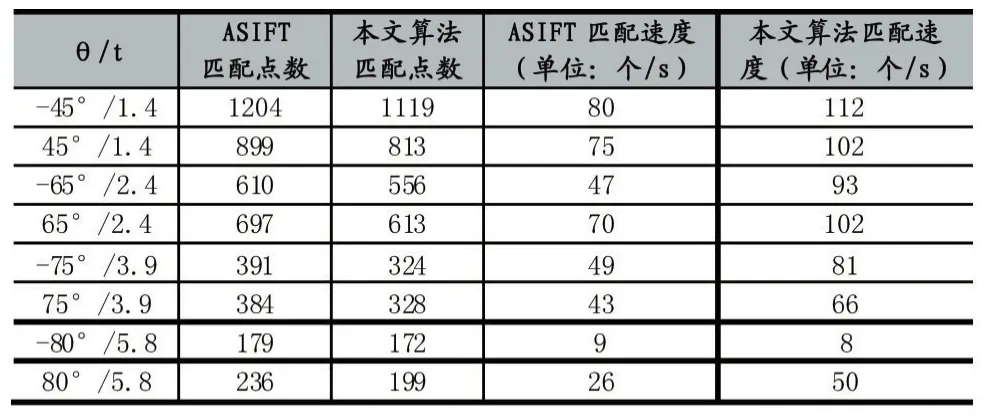
表1 絕對傾斜實驗結果

本文算法得到的匹配點數量相對于ASIFT有所減少，平均下降了10%左右。在基于圖像局部特征描述符的匹配算法中，選擇的描述符對關鍵點的區分能力越高，關鍵點的獨有特征被描述的越充分最后得到的匹配點的數量就會越多，然而這種描述符的生成過程往往非常復雜，在匹配時的計算量較大。本文為了提高匹配速度，在SIFT描述符的基礎上進行簡化操作，最后使用32維描述符執行匹配任務，由于降維后的描述符對于關鍵點的區分能力相對于SIFT描述符有所下降，所以最終匹配點的數量有所減少，但是平均仍然保持在ASIFT 90%左右，最好的情況可以達到96%，從后續的實驗結果中可以看到在相對傾斜較大的情況下甚至超過了ASIFT。在使用最近次近距離算法建立匹配關系時，使用本文簡化后的描述符代替SIFT描述符計算歐氏距離，每一對描述符的計算次數可以減少64次，所以本文算法執行匹配任務時大大降低了計算量，實驗數據表明本文算法的匹配速度平均約為ASIFT的1.5倍。

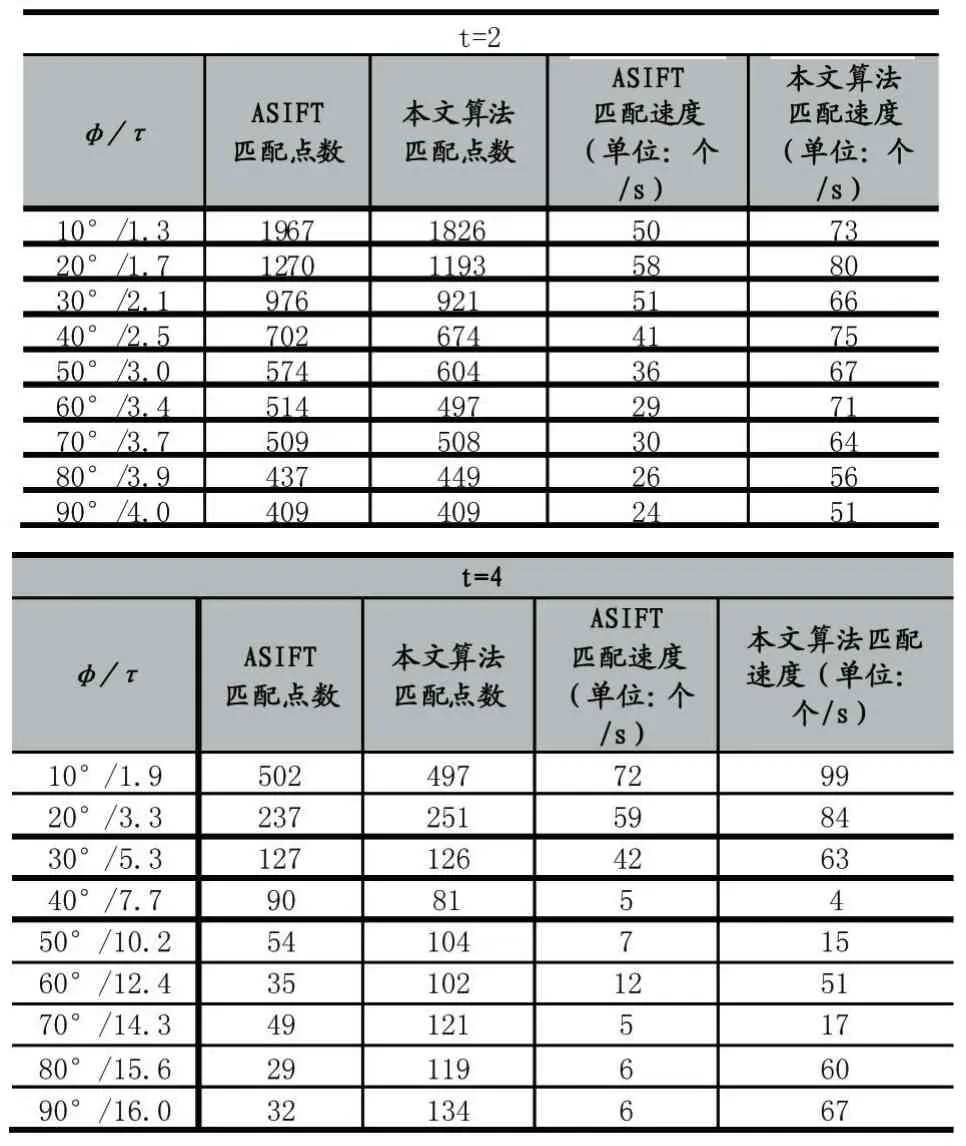
表2 相對傾斜實驗結果

2.2 相對傾斜實驗分析

表2記錄了相對傾斜圖像集上的實驗結果，各列含義與表1基本相同，不過此時第一列表示相對傾斜的變化。由表中數據可知，本文算法在絕對傾斜等于2的相對傾斜圖像集上得到的匹配點數相對于ASIFT有所減少，匹配速度明顯提高與絕對傾斜的實驗結果規律一致，但是當絕對傾斜增大至4時，隨著圖像之間相對傾斜的逐漸增大，本文算法得到的匹配點數超過了ASIFT,尤其是當相對傾斜大于10的時候，該規律非常明顯，而且此時的匹配速度平均是ASIFT的6倍左右。隨著圖像仿射形變的增大，圖像上可以檢測到的關鍵點的數量會逐漸減少，而且描述符之間的相似度也會越來越大因此發生錯誤匹配的概率也會隨之增加，另外本文算法使用的簡化描述符對不同關鍵點的區別能力不如SIFT描述符，所以當圖像之間的仿射形變較大時本文算法得到的錯配點可能會更多。如圖7所示，本文算法得到的匹配點數雖然多于ASIFT,但是也引入了更多的錯誤匹配點。

圖5 相對傾斜為14.3的圖像對的匹配結果

3 結語

本文針對SIFT描述符維度過高、不具備仿射不變性的缺陷，將簡化描述符算法與ASIFT模擬機制相結合提出一種完全仿射不變的圖像匹配算法，實驗數據表明該算法對于仿射形變較大的圖像依然可以穩定工作，而且本文算法的匹配速度明顯快于ASIFT。本文算法使用的簡化描述符對于圖像中關鍵點的區別能力不如SIFT描述符，在初次匹配結果中引入了更多的重復匹配，增加了去除重復匹配的時間開銷，不利于匹配速度的優化，有時甚至導致匹配速度低于ASIFT,相對傾斜為7.7的實驗結果便屬于此類情況。為了解決該問題，下一步考慮結合核密度估計理論建立圖像之間的匹配關系。

[1]David G Lowe,Distinctive Image Features from Scale-Invariant Keypoints,IEEE International Journal of Computer,vol 60,pp.91-110,2004.

[2]Ke Y,Sukthankar R.PCA-SIFT:A More Distinctive Representation for Local Image Descriptors.Proceedings of the 2004 IEEE Computer Society Conference on IEEE,vol.2,2004,pp.506-513.

[3]Z.Zhou,S.Cheng and Z.Li.MDS-SIFT:An Improved SIFT Matching Algorithm Based on MDS Dimensionality Reduction.2016 3rd International Conference on Systems and Informatics（ICSAI）,Shanghai,2016,pp：896-900.

[4]X.Zhou,K.Wang and J.Fu.A Method of SIFT Simplifying and Matching Algorithm Improvement.2016 International Conference on Industrial Informatics-Computing Technology,Intelligent Technology,Industrial Information Integration（ICIICII）,Wuhan,2016,pp.73-77.

[5]Matas J,Chum O,Urban M,et al.Robust Wide-Baseline Stereo from Maximally Stable Extremal Regions[J].Image and Vision Computing,2004,22（10）:761-767.

[6]W.Hu,W.Zhou and J.Guan.A Modified M-SIFT Algorithm for Matching Images with Different Viewing Angle.2016 IEEE International Conference on Signal and Image Processing（ICSIP）,Beijing,2016：247-250.

[7]Morel J M,Yu G.ASIFT:A New Framework for Fully Affine Invariant Image Comparison[J].SIAM Journal on Imaging Sciences,2009,2（2）:438-469.

[8]Fischler M A,Bolles R C.Random Sample Consensus:a Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J].Communications of the ACM,1981,24（6）:381-395.

[9]Moisan L,Stival B.A Probabilistic Criterion to Detect Rigid Point Matches Between Two Images and Estimate the Fundamental Matrix[J].International Journal of Computer Vision,2004,57（3）:201-218.

[10]Lindeberg T.Scale-Space Theory:A Basic Tool for Analyzing Structures at Different Scales[J].Journal of Applied Statistics,1994,21（1-2）:225-270.

[11]C.Harris and M.Stephens.A Combined Corner and Edge Detector,in Proceedings of the Fourth Alvey Vision Conference,Vol.15,1988：147-151.

[12]K.Mikolajczyk and C.Schmid,Indexing Based on Scale Invariant Interest Points,in Proceedings of the 8th International Conference on Computer Vision（ICCV）,2001：525-531.

[13]K.Mikolajczyk and C.Schmid,Scale and Affine Invariant Interest Point Detectors,Int.J.Comput.Vis.,60（2004）：63-86.

[14]D.Lowe,Distinctive Image Features from Scale-Invariant Key Points,Int.J.Comput.Vis.,60（2004）：91-110.

[15]L.F evrier,A Wide-Baseline Matching Library for Zeno,Internship Report.http://www.di.ens.fr/～fevrier/papers/2007-Internsip ReportILM.pdf（2007）.

[16]K.Mikolajczyk and C.Schmid.An Affine Invariant Interest Point Detector,in Proceedings of the Seventh European Conference on Computer Vision（ECCV）,Springer-Verlag,London,2002：128-142.

[17]K.Mikolajczyk and C.Schmid.A Performance Evaluation of Local Descriptors,in Proceedings of the International Conference on Computer Vision and Pattern Recognition,Vol.2,2003,pp.257–2.