基于動態參數蟻群算法的云制造服務組合

張嚴凱，周井泉，李 強

(南京郵電大學 電子科學與工程學院，江蘇 南京 210003)

0 引 言

隨著科技的進步，制造業的規范更加標準和統一。很多復雜產品由一家廠商完成轉向由多家廠商合作完成，達到制造任務和資源的共享。廠商不再僅限于提供單一的產品或零件，而是轉而提供制造能力。制造商的制造能力通過網絡集合形成資源池，即傳統的制造模式轉變為云制造。

云制造是2010年開始出現的概念，綜合國內外對云制造概念的闡述[1-2]，定義如下：云制造(Cloud Manufacturing)是一種基于互聯網的面向服務、效率高、功耗低的新型制造模式。用戶可以根據自己的需求動態調整制造資源。云制造平臺有多種容錯技術。單個物理節點發生故障，云制造平臺都會在后臺將制造轉移到其他的資源上繼續完成，因此云制造模式比傳統的制造模式更具有安全性和可靠性。

關于蟻群算法和云制造服務組合已有不少研究成果，例如陶飛等[3]對云制造服務組合建模、結果評估和組合優選等問題進行了研究和討論；敬石開等[4]以服務模型庫為基礎通過粒子群算法得到了較好的云制造服務組合模型；TRUNK等[5]基于采樣語義匹配查找服務組合，并通過遺傳算法(PSO)進行服務組合優化；劉衛寧等[6]提出了一種采用全局策略選擇基礎服務進行組合的方案；夏亞梅等[7]提出一種多信息素動態更新的蟻群算法(MPDACO)，可以更好得適應動態QoS變化的情況。

在此基礎上，文中提出了一種動態參數蟻群算法，在一定程度上改善了算法的收斂速度，減小了陷入局部最優解的概率。

1 問題描述

1.1 云制造服務組合

云制造是信息技術、制造技術、物聯網技術相互融合的產品。各地閑置的制造資源聚合到資源云池中，用戶向云制造平臺發送制造任務需求，云制造平臺通過服務組合優選為用戶匹配最優制造資源[8-9]。三者的關系如圖1所示。

圖1 云制造模式結構關系

1.2 評價模型

QoS(Quality of Service)模型[10-11]是當前使用最多的評價模型之一。文中的QoS包含四個方面，分別是成本C(Cost)、時間T(Time)、質量函數Q(Quality function)、滿意度S(Satisfaction)。由此可見，QoS評價模型是多目標優化模型。評價函數如下：

(1)

2 云制造服務組合優化算法

2.1 基于蟻群算法的云制造服務組合優化算法

蟻群算法于1992年首先被意大利學者DORIGO M提出，是一種為復雜的優化問題選最優解的種群智能算法。它的基本思想是利用蟻群的合作通過路徑上的信息素來尋找最短路徑。蟻群算法已經普遍應用于組合優化問題[12-15]。云制造服務組合優化過程如圖2所示。原始的云制造任務被分解為n個子任務CMT(Cloud Manufacturing Task)，每一個任務表示為CMTi,i∈[1,n]。

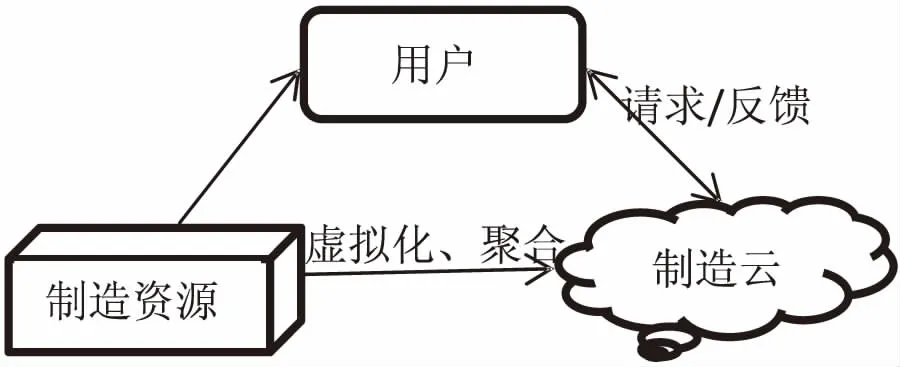
圖2 云制造資源的服務傳遞過程

制造商提供的資源節點稱作CRSN(Cloud Resource Service Node)。每一個資源節點表示為CRSNij,i∈[1,n],j∈[1,m]。這些資源服務節點被動態地匹配給每一個子任務，每個子任務對應的云制造資源被稱為CMR(Cloud Manufacturing Resource)，它們分別表示為CMRj,j∈[1,m]。Lij,(i+1)k表示螞蟻可能的轉移路徑，即每一個子任務對應的最優云制造資源。

原始蟻群算法的具體實現步驟如下：

Step2：將M只螞蟻放于起始位置，令k=0，k為第k只螞蟻。

Step3：迭代次數增加一次，Nc=Nc+1。

Step4：螞蟻數量增加1，k=k+1。

(2)

Step6：如果螞蟻的數量大于最大值M，則進入Step7；否則進入Step4。

Step7：根據式(3)～(5)更新每條線路上的信息素。

τij,pq(t+1)=ρ·τij,pq(t)+Δτij,pq(t)

(3)

(4)

(5)

其中,ρ(0<ρ<1)表示信息素殘留系數，用1-ρ表示信息素的揮發系數。

Step8：如果Nc大于最大迭代次數，則輸出最優評價函數F及分配方案，結束循環；否則進入Step3。

2.2 算法改進策略

2.2.1 不同階段參數動態改變

該算法可分為前期、中期和后期三個階段，前期選擇較高的信息素殘留因子ρ，較小的期望啟發式因子β；中期適當降低ρ的大小，適當增大β；后期選擇較小的ρ，選擇較高的β。前期較高的ρ和較低的β保證了算法能夠有較好的全局搜索能力，很難陷入局部最優解;后期較低的ρ和較高的β加快了算法的收斂速度，提高了算法效率。

2.2.2 加入特殊螞蟻

(6)

前期使用較多的特殊螞蟻能夠有效地跳出局部最優解，有利于尋找到全局最優解。

2.3 基于動態參數蟻群算法的云制造服務組合優化算法

動態參數蟻群算法(DPACO)的具體步驟如下：

Step2:前期階段將M只常規螞蟻和S1個特殊螞蟻放在起始位置；中期階段將M只常規螞蟻和S2個特殊螞蟻放在起始位置，S2可取S1/2；后期階段將M只常規螞蟻放在起始位置，此時無特殊螞蟻。

Step3:迭代次數加1，Nc=Nc+1。

Step4:常規螞蟻開始搜索，根據式(2)確定狀態轉移概率。前期階段β=βlow，將β設為較小值，可取2；中期階段β=βmid，將β設為中間值，可取3；后期階段β=βhigh，將β設為較大值，可取5。此時為常規螞蟻，選擇概率較大的服務，將螞蟻移動到該服務下。

Step6:常規螞蟻和特殊螞蟻都搜索完成時，根據式(3)～(5)更新每條路徑上的信息素。前期階段ρ=ρlow，ρ設為較小值，可取0.1；信息素范圍τij(t)∈[τmin,τmax]。中期階段ρ=ρmid，ρ設為中間值，可取0.25；信息素范圍τij(t)∈[τmin,τmax]。后期階段ρ=ρhigh，ρ設為較大值，可取0.4；信息素范圍τij(t)∈[0,+]。

Step7:判斷迭代次數是否達到最大，若達到，進入Step8，否則進入Step3。

Step8:再進行5次迭代，并記錄5次迭代的適應度值，求出5次適應度值的方差。

Step9:如果方差大于所設定的方差S2(S2趨于0)，進入Step8，否則在后期階段則輸出優選結果，在其他階段則進入下一個階段。

3 實驗分析

通過一個鋼鐵制造企業的鋼鐵鍛造任務來驗證提出的基于動態參數的蟻群算法。由于任務需求和該企業自身能力的限制，此鍛造任務需要和其他企業合作完成。這個任務現在被分為5個子任務，即{CMT1,CMT2,CMT3,CMT4,CMT5}。每個子任務及對應的制造資源如圖3所示。

圖3 鋼鐵鍛造任務云資源圖

使用的每一個制造資源都有對應的成本、時間、質量、滿意度，具體的數值見表1。

由表1可知，對于不同的參數值它們有不同的單位和數量級。為了方便數據處理，需要進行歸一化，如下所示：

y=(x-min)/(max-min)

(7)

其中，y為歸一化后的新數據；x為原始數據；min、max分別表示此類參數的最小值和最大值。

歸一化后，使用不同的算法進行求解。此次實驗的環境是宏基4750G，Intel(R) Core(TM) i5-2410M CPU 2.3 GHz主頻，軟件是MATLAB2014A，由經驗設定初始參數M=20,α=1,β=5,ρ=0.4,P=20,w1=w2=0.2,w3=w4=0.3。不同算法的實驗結果見表2和圖4，從中可以看出DPACO比其他算法有更快的收斂速度，更好的穩定性。

表1 云資源對應的C、T、Q、S值

表2 不同算法的結果對比

圖4 不同算法的適應度值對比

4 結束語

以基于成本C、時間T、質量函數Q、滿意度S的QoS模型作為評價函數來評價改進蟻群算法選擇結果的優劣。提出的動態參數蟻群算法通過改變不同階段參數的值和加入特殊螞蟻等策略，改進了收斂慢、易陷入局部最優等缺點。通過實驗結果分析得知，改進算法能夠有效地解決云制造服務組合問題，在效率上明顯優于ACO、DE、PSO。下一步的研究工作將集中探索更高效率的群智能算法以解決服務組合問題。

[1] XU X.From cloud computing to cloud manufacturing[J].Robotics and Computer Integrated Manufacturing,2012,28(1):75-86.

[2] 李伯虎,張 霖,柴旭東.云制造概論[J].中興通訊技術,2010(4):5-8.

[3] 陶 飛,張 霖，郭 華,等.云制造特征及云服務組合關鍵問題研究[J].計算機集成制造系統,2011,17(3):477-486.

[4] 敬石開,姜 浩,許文婷,等.考慮執行可靠性的云制造服務組合算法[J].計算機輔助設計與圖形學學報,2014,26(3):392-400.

[5] TRUNK A.QoS-aware service composition:a survey[C]//Proceedings of the 8th IEEE European conference on web services.Washington D C,USA:IEEE,2010:67-74.

[6] 劉衛寧，劉 波，孫棣華.面向多任務的制造云服務組合[J].計算機集成制造系統，2013,19(1):199-209.

[7] 夏亞梅，程 渤，陳俊亮,等.基于改進蟻群算法的服務組合優化[J].計算機學報,2012,35(2):270-281.

[8] 劉 波.云制造環境中面向多任務的服務組合與優化技術研究[D].重慶:重慶大學,2012.

[9] 常瑞云,周井泉,許 斌,等.基于離散人工群算法的云制造服務組合[J].計算機技術與發展,2016,26(7):177-182.

[10] 劉家良,孫俊麗,姜利群.一種面向云計算的QoS評價模型[J].電腦知識與技術,2010,6(31):8801-8803.

[11] 齊 軒,劉茜萍.基于用戶偏好的可信QoS服務選擇方法[J].計算機技術與發展,2016,26(8):43-47.

[12] DORIGO M,GAMBARDELLA L M.Ant colonies for the travelling salesman problem[J].Biosystems,1997,43(2):73-81.

[13] BELL J E,MCMULLEN P R.Ant colony optimization techniques for the vehicle routing problem[J].Advanced Engineering Informatics,2004,18(1):41-48.

[14] MAIER H R.Ant colony optimization for design of water distribution systems[J].Journal of Water Resources Planning and Management,2003,129(3):200-209.

[15] MCMULLEN P R.An ant colony optimization approach to addressing a JIT sequencing problem with multiple objectives[J].Artificial Intelligence in Engineering,2001,15(3):309-317.