基于分布式計算模式的兩種屬性約簡算法
喻 瑛,楊 崢,王偉杰
(上海大學 機電工程與自動化學院,上海 200072)
0 引 言
粗糙集是處理不確定、不完備數據的經典理論。屬性約簡是粗糙集理論的核心知識之一,屬性約簡的目標在于發現必要的條件屬性,使得根據這些條件屬性而形成的相對于決策屬性的分類和所有條件屬性所形成的相對于決策屬性的分類一致,即保持原有的分類能力[1]。屬性約簡算法主要有基于正域的屬性約簡算法[2-3]、基于信息熵的屬性約簡算法[4-5]、基于差別矩陣的屬性約簡算法[6]等。
隨著信息通訊技術和云計算技術的發展,各行業領域數據逐年呈指數級增長。為適應大數據發展,文中提出了兩種適應分布式處理機制的改進屬性約簡算法。首先基于MapReduce分布式計算框架,探討了基于正域的屬性約簡算法;然后借鑒Hadoop分布式處理機制,提出了一種新型的分布式處理機制和數據分割分布規則,并在此基礎上提出了基于分布式處理機制的差別矩陣屬性約簡算法。
1 粗糙集屬性約簡理論
1.1 粗糙集相關概念
定義1(決策信息表):決策信息表S={U,A,V,f}是一個信息系統的表達,其中U為對象集合,亦稱為論域;R=C∪D,為屬性集合,其中C為條件屬性集,D為決策屬性集;V為屬性值集合;f:U×R→V為信息函數,它指定U中每個對象x的屬性值[7-8]。
定義2(不可區分關系):在決策表S中,對屬性子集B?R,定義不可區分關系IND(B),即:IND(B)={(x,y)|(x,y)∈U×U,?b∈B,b(x)=b(y)}。
定義3(上近似集和下近似集):在信息系統S={U,A,V,f}中,設X?U是個體全域上的子集,P?A。則X的下近似集和上近似集分別定義為:
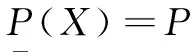
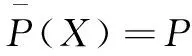
定義4(正域):在信息系統S={U,C∪D,V,f}中,設D*={X1,X2,…,Xm},屬性子集P(P?C)關于決策屬性D的“正區域”定義為:
P關于D的正區域表示根據屬性子集P就能正確區分的所有對象的集合。
定義5(約簡):設U為論域,P和Q分別為定義在U上的兩個等價關系簇,若P的Q獨立子集S?P有POSS(Q)=POSP(Q),則稱S為P的Q約簡。
定義6(核):屬性C的所有約簡的交集稱為核,記作:CORE(C)=∩RED(C)。核表示C中對于所有約簡都不可缺少的屬性集合。與約簡不同,核一定是唯一的,但可能為空集。
1.2 粗糙集屬性約簡
知識約簡是指在保持知識庫分類或決策能力不變的前提條件下剔除冗余屬性知識,得到最簡屬性集的過程[9]。常見的典型屬性約簡方法有三種:主成分分析法[10]、奇異值分解法[11]、基于粗糙集的屬性約簡[12-14]。主成分分析法利用降維的思想將不同屬性上的信息轉換到主成分上面,易造成某些重要信息的缺失。奇異值分解法是矩陣分析中正規矩陣酉對角化的推廣,在分析數據時往往因直接舍棄某些信息而造成部分有用信息缺失。基于粗糙集的屬性約簡可在保持信息系統分類能力和決策能力不變的前提下,刪除系統中不必要的屬性[15]。相比于前兩種方法,其約簡結果更加可靠、準確。
2 基于正域和MapReduce的屬性約簡算法
2.1 基于正域的屬性約簡算法流程
輸入:決策表T={U,C∪D},C={c1,c2,…,cm},其中C,D分別為條件屬性集和決策屬性集。
輸出:約簡Red(C,D)。
步驟:
(1)令Core(C,D)=?,計算POSC(D);
(2)對每個a∈C,計算POSC-{a}(D),如果
POSC(D)≠POSC-{a}(D),則Core(C,D)=Core(C,D)∪{a};
(3)令B=Core(C,D),如果
POSB(D)=POSC(D),則轉向(5),否則轉向(4);
(4)對?a∈CB,求

(5)輸出Red(C,D)=B。
算法中,POSC(D)、POSC-{a}(D)、POSB(D)等正域計算應用MapReduce計算模式完成。
2.2 基于正域和MapReduce的屬性約簡算法流程
以POSC(D)為例,基于MapReduce計算模式的正域計算算法流程如下:
輸入:決策表T={U,C∪D},C={c1,c2,…,cm},其中C,D分別為條件屬性集和決策屬性集。
輸出:正域POSC(D)。
步驟:
(1)基于MapReduce框架計算IND(D);
(2)基于MapReduce框架計算IND(C);
(3)計算POSC(D)。
3 基于分布式處理機制的差別矩陣屬性約簡方法
3.1 分布式計算處理機制
基于差別矩陣的屬性約簡是常用的屬性約簡方法,差別矩陣具有all-to-all[7]比較特性,為在分布式計算模式下運用差別矩陣進行屬性約簡,需要設計一種有效的分布式處理機制和數據分配及調度機制實現all-to-all比較。文中借鑒Hadoop平臺傳統的分布式計算模式,針對基于Hadoop平臺的MapReduce計算框架在數據調度方面靈活性不足的特點,在此基礎上設計了一種新型的分布式計算模式和數據調度機制。最后基于該規則探討基于分布式處理機制的差別矩陣屬性約簡算法。
首先給出分布式計算機制。該機制主要由Master和DataNode兩部分組成,Master機器負責數據的分割、預調度、調度分配和分布式算法發布工作;DataNode接收到由Master傳來的數據和分布式算法分布完畢的消息后進行分布式計算,并將運算結果返回給Master,最終由Master對返回結果進行歸并等處理。
3.2 數據分布規則
為實現差別矩陣的all-to-all比較,各分布式的DataNode需要放置部分重復數據塊,如何規劃數據塊分割和預調度,使重復數據塊最小,以實現數據空間占用最小化,是一個優化組合問題。文獻[7]提出了以最小化數據空間占用實現all-to-all比較的數據調度啟發式算法,但其數據調度在各DataNode上分配不均勻,算法運行時間受到數據分配最大的機器的運行時間制約,因此算法運行時間具備不確定性。文中提出了一種新型數據分布規則,配以簡單的算法實現,不僅可在實現all-to-all比較的同時最小化數據空間占用,而且可以大致確定機器運行時間。
該分配規則如下:假設有3臺DataNode,先將數據平均等分為X1、X2、X3份,后再各等分2份,即共分為X1,1、X1,2、X2,1、X2,2、X3,1、X3,2。
每臺DataNode數據量為總數據量的2/3。將上述的數據分配規則推廣到DataNode數量l>3,得定理1。
定理1:對于l臺DataNode,將數據按以下規則分配,可實現all-to-all比較。
(1)將數據l等分為l(l≥3)個數據塊,將數據塊按順序編號為X1,X2,…,Xl,對l個數據塊各自二等分,編號為X1,1,X1,2,X2,1,X2,2,…,Xl,1,Xl,2。
(2)在DataNode1分配數據X1,1,X1,2,以及所有數據塊Xi,1(i=3,4,…,l)。
(3)在DataNode2分配數據X2,1,X2,2,以及所有數據塊Xi,2(i=3,4,…,l)。
(4)在任意DataNodei(i>3)上:
(4.1)分配數據Xi,1,Xi,2;
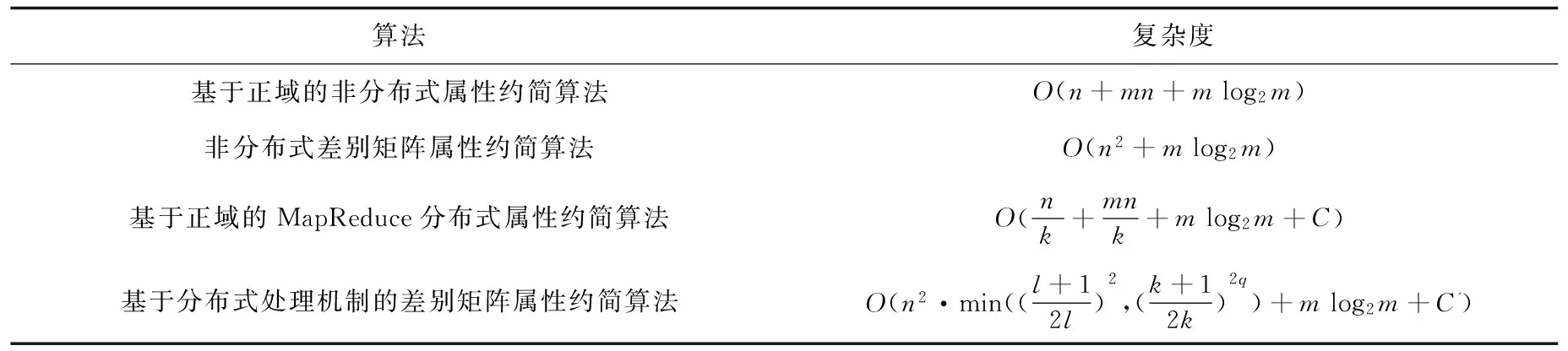
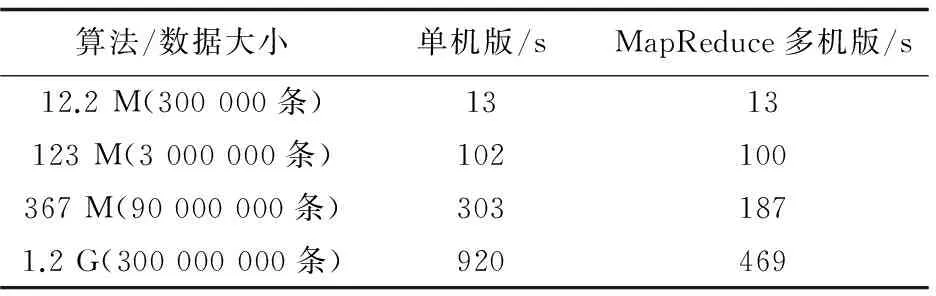
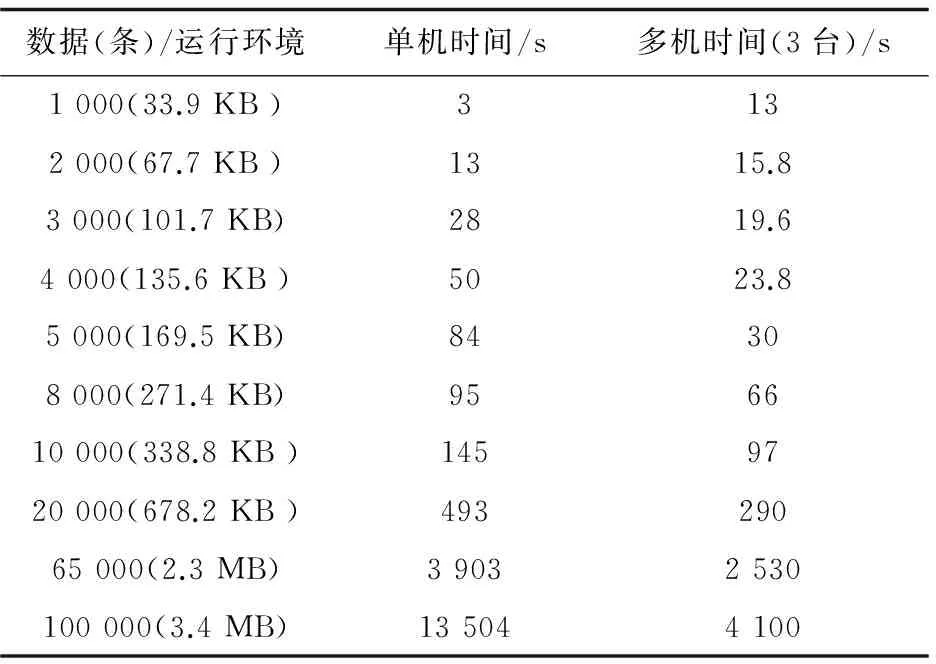
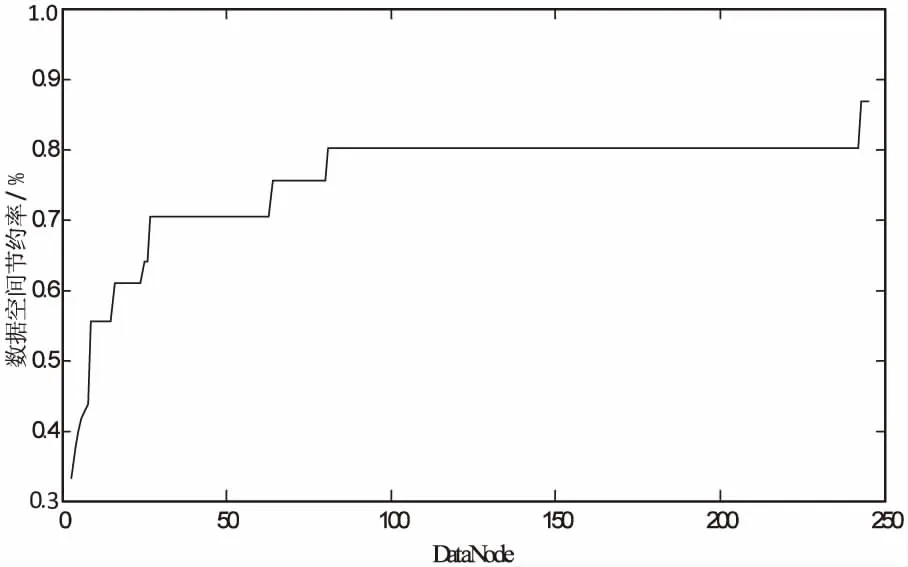
(4.2)對于數據塊(Xi-r,1,Xi-r,2)(0 (4.3)對于數據塊(Xi+p,1,Xi+p,2)(p>0),如果i為奇數,分配數據Xi+p,1,如果i為偶數,分配數據Xi+p,2。 證明: 對于任意兩個數據塊Xi、Xj(i>j),各自再二等分后成為Xi,1、Xi,2、Xj,1、Xj,2,要實現all-to-all比較,構造差別矩陣生成數據對如下: 依據規則可知,(Xi,1,Xj,1)在DataNode1上,(Xi,2,Xj,2)在DataNode2上;i為奇數時,(Xi,2,Xj,1)在DataNodei上,(Xi,1,Xj,2)在DataNodej上;i為偶數時,(Xi,1,Xj,2)在DataNodei上,(Xi,2,Xj,1)在DataNodej上。 按此規則分配數據,可實現all-to-all比較。 當DataNode數量l=2k+2時,數據分配結果如表1所示(當l=2k+1時,數據分配結果如表1的列1~7所示)。顯然,表1所示的數據分割分配結果可實現all-to-all比較。 在分布式計算處理機制及數據分布規則提出的基礎上,現整理算法流程如下: 輸入:配置到Master上的全局數據文件,DataNode數量l。 輸出:完成數據分割,并將局部數據文件發布到各DataNode上。 步驟: (1)計算l所在區間[kq,(k+1)q]的所有k值與q值,求出使空間節約率最大的k值與q值; (3)將數據等分成2l個局部數據文件,按DataNode數為l的數據分布規則發布到l臺DataNode上,轉到步驟(13); (4)令r=1,Dr={d1|d1=全局數據文件}; (5)Whilej1≤qdo (6)Dj1+1=? (7)Whilej2≤|Dj1| do Dj1+1=Dj1+1∪{d|Dj1+1|+1,d|Dj1+1|+2,…,d|Dj1+1|+k}; (10)j2=j2+1; (11)j1=j1+1; (12)結束。 各DataNode分別執行的差別矩陣屬性約簡算法流程如下: 輸入:決策表T={U,C∪D},C={c1,c2,…,cm},其中C,D分別為條件屬性集和決策屬性集,對象個數為ni; 輸出:析取、合取后的邏輯式。 步驟: (1)求差別矩陣: M(i,j)= (2)對差別矩陣進行析取、合取邏輯運算。 (3)在Master上進行歸并處理,對各DataNode返回的析取、合取邏輯式繼續進行合取,輸出約簡Red(C,D)。 基于正域的非分布式屬性約簡算法、非分布式差別矩陣屬性約簡算法、基于正域的MapReduce分布式屬性約簡算法、基于分布式處理機制的差別矩陣屬性約簡算法的時間復雜度對比如表2所示。 表2 算法的時間復雜度對比 其中,n為對象記錄條數,m為條件屬性個數,l為DataNode個數(kq≤l≤(k+1)q),C為基于正域和MapReduce的屬性約簡算法中Master與DataNode之間數據交換與通信時間,C'為基于分布式處理機制的差別矩陣屬性約簡方法中Master與DataNode之間數據交換與通信時間。 應用包含10個條件和1個決策屬性的數據集,取不同對象記錄條數,應用文中提出的兩種算法進行屬性約簡。應用基于MapReduce計算模式的正域計算算法進行屬性約簡,其運行時間與單機版正域算法的時間對比如表3所示。 表3 運行時間對比(基于MapReduce計算模式的正域計算算法) 應用基于分布式處理機制的差別矩陣屬性約簡算法,其運行時間與單機版差別矩陣屬性約簡的時間對比如表4所示。由表3與表4比較可知,基于MapReduce計算模式的正域計算算法在計算時間上優于基于分布式處理機制的差別矩陣屬性約簡算法。 表4 運行時間對比(基于分布式處理機制的差別矩陣屬性約簡算法) 將DataNode數量進行擴展,應用基于分布式處理機制的差別矩陣屬性約簡算法進行屬性約簡,應用文中提出的數據分布機制,其數據空間節約率與文獻[9]、Hadoop機制的對比如表5所示。 表5 數據空間節約對比 % 從表5可以看出,隨著DataNode數量的不斷增加,文中提出的數據分割方式在數據空間節約率效用上逐漸接近甚至部分優于文獻[9]與Hadoop的處理結果。而且,文獻[9]與Hadoop在各臺DataNode上分配的數據不均勻,計算時間將受分配數據量最大的DataNode的計算時間影響,而文中提出的數據分配規則,數據在各臺DataNode上均勻分配,計算時間可以大致確定,相比文獻[9]與Hadoop來說,在處理方式上更加便捷。 隨著DataNode數量的增加,數據空間節約率變化如圖1所示。從圖1可以看出,隨著機器臺數的增加,基于分布式處理機制的差別矩陣屬性約簡算法的數據空間節約率在逐漸增加。由此進一步驗證了算法的有效性。 圖1 數據空間節約率變化 為適應大數據發展的需要,首先在MapReduce分布式計算框架下提出了基于正域的屬性約簡算法;然后針對差別矩陣的all-to-all計算特性,基于Hadoop分布式計算理念,設計了一種可自行處理數據分布的分布式計算模式,并提出了數據在DataNode間的新型分配規則和相應算法,基于此提出了基于分布式處理機制的差別矩陣屬性約簡方法。仿真算例表明,兩種算法均具有可行性;相對于文獻[9]和Hadoop的數據分配機制,文中提出的DataNode數據分配規則不僅處理效率更優,在數據空間節約率上也接近或部分更優。而且,該數據分布機制不僅適用于差別矩陣算法,還可推廣應用于其他所有all-to-all類型的比較。此外,從運行時間對比來看,基于MapReduce計算模式的正域計算算法優于基于分布式處理機制的差別矩陣屬性約簡算法,該差別矩陣算法在運行時間方面還有進一步改進空間,這將是下一步的研究方向。 [1] 王 宇,楊志榮,楊習貝.決策粗糙集屬性約簡:一種局部視角方法[J].南京理工大學學報:自然科學版,2016,40(4):444-449. [2] 黃國順.保正域的決策粗糙集屬性約簡[J].計算機工程與應用,2016,52(2):165-169. [3] 劉濤濤,馬福民,張騰飛.基于正區域和差別元素的增量式屬性約簡算法[J].計算機工程,2016,42(8):183-187. [4] 劉城霞,何華燦.基于信息熵的屬性約簡算法研究與實現[J].北京信息科技大學學報:自然科學版,2015,30(4):56-60. [5] 李少年,吳良剛.基于鄰域信息熵度量數值屬性快速約簡算法[J].計算機工程與科學,2016,38(2):350-355. [6] 王治和,崔曉慧.改進的差別矩陣啟發式屬性約簡算法[J].計算機工程與設計,2016,37(4):1032-1036. [7] NASIRI J H,MASHINCHI M.Rough set and data analysis in decision tables[J].Journal of Uncertain Systems,2009,3(3):232-240. [8] 朱 繼,喻 瑛,王辰煒,等.基于粗糙集合自適應遺傳算法的電力變壓器故障診斷[J].電測與儀表,2012,49(6):47-51. [9] ZHANG Y, TIAN Y, FIDGE C, et al. Data-aware task scheduling for all-to-all comparison problems in heterogeneous distributed systems[J].Journal of Parallel & Distributed Computing,2016,93-94:87-101. [10] 錢 程,穆文平,王 康,等.基于主成分分析的地下水水質模糊綜合評價[J].水電能源科學,2016,34(11):31-35. [11] 馬宗杰,劉華文.基于奇異值分解-偏最小二乘回歸的多標簽分類算法[J].計算機應用,2014,34(7):2058-2060. [12] BILSKI P.Data set preprocessing methods for the artificial intelligence-based diagnostic module[J].Measurement,2014,54:180-190. [13] WANG J,LIU J.Fault diagnosis of wind turbine based on rough set and BP network[C]//Advances in computer science research.Paris:Atlantis Press,2015:877-883. [14] YANG Q J.Study on computer network application layer fault diagnosis based on RSNN:advanced materials research[J].Advanced Materials Research,2014,846-847:1423-1426. [15] 韓 玉,李美聰,郭新辰.基于粗糙集理論的文本分類屬性約簡算法[J].東北電力大學學報,2016,36(5):92-96.
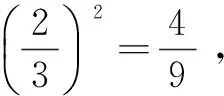
3.3 數據分割及配置算法
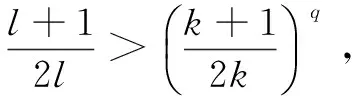
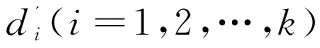

3.4 算法步驟
4 算法的時間復雜度比較
5 仿真算例

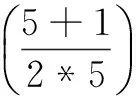
6 結束語

