基于融合特征的群體行為識別

譚程午，夏利民，王 嘉

(1.中南大學 信息科學與工程學院，湖南 長沙 410075；2.國防科技大學 訓練部，湖南 長沙 410073)

0 引 言

人體行為識別是計算機視覺的重要研究課題，有著廣闊的應用前景。人體行為識別可以分為3個方面：個人行為識別、交互行為識別、群體行為識別。群體行為分析和理解是計算機視覺、圖像處理等領域中的重要研究課題。以出發點不同將群體行為分析分為宏觀和微觀兩大類。宏觀是以整體為出發點，將整個群體看作一個整體，從全局來分析群體行為。Ernesto等[1]通過利用光流法以及無監督的提取特征法對高密度群體事件進行識別。Ge等[2]則是利用伯努利形狀模型對群體中的人數進行統計。Kratz等[3]利用時空運動模型對群體異常行為進行檢測。胡波等[4]通過利用灰度共生矩陣對人群密度進行估計。Xiong等[5]利用能量模型檢測群體異常行為。此類方法對于大規模群體以及具有共同運動模式的群體很適用，然而忽視了運動方向、個體位置等特征，所以對于松散運動模式的群體行為并不適用。而微觀則是以群體中的個體為出發點，對個體進行目標跟蹤[6-8]，利用目標的姿態、運動軌跡對群體行為進行識別。Tu等[9]通過人的頭部和肩部對人體進行定位。Blunsden等[10]利用AdaBoost分類器對行為視頻中的異常行為進行檢測。Guo等[11]通過建立運動模型以及外觀形狀來識別群體行為。胡芝蘭等[12]利用目標的運動方向對走廊內的群體異常行為進行檢測。此類方法不能有效描述行人間的相互作用以及人群的整體表現。因為小規模群體通常包含兩到三人，并且群體間的運動具有某種關聯性，所以分析小規模群體行為的方法既包括宏觀特性，又包括微觀特性。

目前大多數方法都是利用群體行為參與者的運動軌跡來描述運動信息[13]。把運動軌跡當作一個動態系統，然后通過馬爾可夫平穩分布計算所提取的特征。Dore等[14]提出了利用統計表示來編碼基于動態貝葉斯網絡的雙軌跡因果關系來分析交互行為的方法。Chu[15]提出一種基于熱圖的算法來進行群體行為識別。首先把軌跡作為一系列熱源，然后利用熱擴散過程做出一幅熱圖來描述群體行為。盡管運動信息對于描述行為模式更直觀，但是外觀信息作為識別特征對于促進理解群體行為是一個很好的補充[16]。利用三維多邊形來描述群體行為的可視結構，但是三維結構對于激烈的群體行為沒有很好的魯棒性，而且不容易精確獲得。Zhu等[13]利用局部外觀信息，如尺度不變特征變換(SIFT)，作為群體行為的一個描述符號。然而，由于群體行為中單個參與者具有外觀差異性，會影響局部外觀特征的可靠性。因此，整體外觀特征對于群體行為的描繪更合適。

針對以上問題，為了既能描述群體中個體運動的微觀特性，同時又能描述群體中潛在的整體信息的宏觀特性，提出了一種基于融合特征的群體行為識別方法。先將各行人目標看成網絡的節點，利用協方差跟蹤獲得目標的運動軌跡，并利用格蘭杰因果關系檢驗來衡量目標之間的相互作用，同時利用此因果關系來構建成雙因果網絡和成群因果網絡，并結合外觀特征來描述群體行為。采用改進螢火蟲算法的支持向量機(SVM)進行分類，提高了分類精度，優化效果顯著。

1 運動特征表示

1.1 網絡的節點的確立

利用群體網絡識別群體行為，首先將群體中的每個目標當作一個節點，將目標之間的因果作用當作邊，相互作用的大小當作網絡權值，以此來構建群體復雜網絡。G(V,E,W)是有向加權圖，利用它來表示群體復雜網絡。為了確定群體復雜網絡節點，需要獲得一段行為視頻中目標的運動軌跡，文中利用多特征融合的協方差匹配算法來進行目標跟蹤。

協方差匹配算法的基本原理是首先在第一幀中對目標模板區域進行初始化,同時計算該目標模板區域的協方差矩陣特征，從而在隨后的每一幀圖像的候選區域中選擇與模板區域最相似的區域進行匹配，將此區域視為目標在當前幀的位置。假設一圖像區域R大小為M×N，(x,y)表示一個像素點，和每一個像素點相對應，fk表示該像素的特征向量，式(1)表示提取該像素的亮度、顏色、空間距離特征以及梯度：

fk=[R(x,y),G(x,y),B(x,y),d(x,y),I(x,y),Ix(x,y),Iy(x,y)]

(1)

(2)

其中，μR表示R中每一個像素點對應特征向量的平均值。

為了確定當前幀中與目標區域最相似的區域，需要對候選區域和目標區域的協方差矩陣之間的距離進行計算[17]。通過計算兩個矩陣的廣義特征值的對數平方和來表示協方差矩陣間的距離，如下式：

(3)

其中，λk(Ci,Cj)表示矩陣Ci,Cj的廣義特征值，利用|λCi-Cj|=0計算。

1.2 網絡的邊的確立

為了構建群體復雜網絡，在確定節點的基礎上，還需要確立網絡的邊。利用目標之間的因果關聯度來衡量目標之間的聯系程度，用成雙因果關系和成群因果關系來表示兩目標間的因果關聯度，同時構建成雙因果網絡和成群因果網絡，然后對兩個網絡的特征參數進行融合，進而進行群體行為識別。

1.2.1 成雙因果

成雙因果關系在描述群體中兩個目標之間的關系時，只考慮兩個目標之間是否存在因果作用以及相互作用的強度，而對于其他目標對這兩個目標的影響是不予考慮的。Zhou[18]提出首先得到目標的運動軌跡，然后利用格蘭杰因果關系檢驗來定量度量兩個目標之間的因果特性，用因果比表示一個目標對另一個目標的作用強度，反饋比表示另一個目標的反作用強度。

Pi(t),Pj(t)分別表示兩目標同時運動的軌跡，假設在一段時間內兩目標運動軌跡的相互作用是一個平穩過程，通過利用q階線性預測器對目標i的運動軌跡進行建模，得到：

(4)

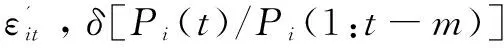
和因果比的計算相似，同樣得到兩個目標之間的反饋比：

反饋比與因果比揭示誤差項的信息，能有效表示兩個目標之間的相互作用強度。由反饋比與因果比可以得到一個n×n的因果關聯強度矩陣gcp，n表示目標的個數，把gcp作為構建成雙因果網絡的依據。

1.2.2 成群因果

一個群體一般包含三人或三人以上的目標，所以在衡量兩目標間的相互作用時，同時應該考慮其他目標的影響。在不包括目標j情況下，δ[Pi(t)/U(1:t-m)-Pj(1:t-m)]表示利用線性回歸方程對目標i預測得到的標準偏差，U表示所有目標的軌跡信息，現包括群體中的所有目標，δ[Pi(t)/U(1:t-m)]表示線性回歸標準偏差，此時得到兩個目標之間的因果比：

(7)

同樣得到兩個目標之間的反饋比：

(8)

將所有目標之間的因果關系計算后，得到一個n×n的因果關聯強度矩陣gcg，n表示目標的個數，把gcg作為構建成群因果網絡的依據。

1.3 因果網絡模型的特征提取

群體行為不同，人群特征也不同，同時構建的群體因果復雜網絡模型也不同。就算是同一種群體行為，目標之間的相互作用不同，每個人在網絡中的重要程度也是不同的。文中利用復雜網絡的統計特征參數來描述人群特征，選擇以下幾個特征參數。

平均路徑長度能夠揭示網絡中各目標節點之間的分離程度，通過計算兩目標節點之間的最短距離得到平均路徑長度。對一個群體復雜網絡中所有兩兩節點間的最短距離取平均值就得到整個群體網絡的平均路徑長度，網絡的平均路徑長度越短表示網絡中節點間的分離程度越小，反之，則分離程度越大。不同的群體行為構建的網絡中兩目標之間的關系不同，計算得到的平均路徑長度也不同，所以利用平均路徑長度來描述群體行為，如下式：

(9)

介數揭示對應目標在整個群體中的作用和影響力，能夠衡量目標在網絡中的重要程度，節點k的介數計算公式如下：

(10)

其中，d(i,j)表示節點i和j之間最短路徑的數目；dk(i,j)表示經過節點k的節點i和j之間最短路徑的數目。

不同的群體行為，影響力最強的目標是不同的，揭示其影響力的介數也不同，影響力最弱的目標也是如此。所以利用介數來反映不同群體行為構成的網絡中影響力最強以及最弱的節點。因此用介數的最大值gmax、最小值gmin、平均值gave作為行為特征。

利用聚合系數描述網絡中各目標的聚集程度，也就是各目標之間到底有多緊密的關系。群體行為不同，目標聯系的緊密程度不同，比如在Linger(徘徊)這個群體行為中，各目標的運動是雜亂無序的，目標聯系相對較松散，聚合系數較小，而Gather(聚集)這個群體行為中,各目標的運動遵循一定的規則，目標聯系相對較緊密，聚合系數較大，所以利用集合系數表示群體行為特征，如下式：

(11)

其中，Ei表示和節點i相連的邊的數目；ki表示和節點i相連的節點的數目。

綜上所述，實驗過程中采用了成雙因果網絡提取的特征向量和成群因果網絡提取的特征向量，以及它們的組合向量。成雙因果網絡特征向量表示如下：

(12)

成群因果特征向量表示如下：

(13)

組合向量表示為：

Vc=[Vp,Vg]

(14)

2 外觀特征表示

除了運動特征以外，整個群體的外觀變化同樣能反映群體行為的識別信息。通過描述群體行為的空間結構及其變化來進行行為識別，稱之為群體形狀。根據某一幀的所有參與者的位置可以形成一個平面多邊形，利用它來描述群體形狀，如圖1(a)所示。然而這些沒有約束的多邊形有著復雜的構造，而且不是一致的跨幀，難以描述，并且丟失了群體中的詳細相關信息。因此采用德勞內三角化代替多邊形描述緊湊而又詳細的結構信息。將一組點的德勞內三角化定義為一個三角形劃分T。如圖1(b)所示，和多邊形相比，德勞內三角化能夠描述更多群體內部結構的信息，并且考慮到了每一個參與者在群體中的影響。利用整體特征和局部特征分別去描述穩定的和變化的群體形狀特征。

圖1 群體形狀圖

整體群體形狀特征：利用三角化的所有三角形的外接圓面積A，邊界E，中心C，從整體角度來描述它的緊密度。這些參數能描述整個三角形劃分的識別信息。為了描述群體行為的即時狀態的穩定特征，定義如下公式：

Rarea=Std(A)/Mean(A)

(15)

(16)

(17)

其中，Std()表示標準差；Mean()表示平均值；Min()表示最小值；Max()表示最大值；Min(E)表示德勞內三角化的邊集E中的最短邊。

根據第i-1幀和第i幀三角形劃分的不同來表示群體形狀的變化。因此面積的改變，中心距離(CDist)的改變以及旋轉變化都要考慮。旋轉為X/Y軸主方向的變化。主方向近似為連接一個軸的最大值的點和最小值點的那條線的方向。公式如下：

Γareai=(Sum(Ai)-Sum(Ai-1))/Sum(Ai-1)

(18)

ΓCDisti=(Mean(CDisti)-Mean(CDisti-1))/

Mean(CDisti-1)

(19)

(20)

(21)

其中，Xmax，Xmin，Ymax以及Ymin表示三角形中在X軸和Y軸的極值點；Sum()表示求和；Angle()表示兩條線之間的夾角。

因此，整體群體形狀特征表示為[Rarea,Redge,Rcenter,Γareai,ΓCDisti,ΓX,ΓY]。

局部群體形狀特征：為了得到更詳細的群體形狀信息，利用每一個三角形來描述群體形狀信息。和整體群體形狀特征類似，假設一共有k個三角形，面積為Ak，邊界為Ek，夾角為Λk，那么可得到穩定的局部特征：

rarea=Ak/∑A

(22)

redgek=Min(Ek)/Max(Ek)

(23)

ranglek=Min(Λk)/Max(Λk)

(24)

根據第i-1幀和第i幀的三角形劃分的不同來描述局部的變化，如下式。

γareaik=Aik-A(i-1)k/A(i-1)k

(25)

γedgeik=Max(Eik)-Max(E(i-1)k)/Max(E(i-1)k)

(26)

γangleik=(Max(Λik)-Max(Λ(i-1)k))/Max(Λ(i-1)k)

(27)

因此，利用[rareak,redgek,ranglek,γareaik,γedgeik,γangleik]來描述局部整體形狀特征。

3 改進螢火蟲算法的SVM

根據螢火蟲算法，螢火蟲發光越亮，表明其所處的位置具有更加優良的目標函數值。每只螢火蟲在自己擁有的視野范圍內，利用動態決策挑選亮度比自己高的螢火蟲，與之結為鄰舍并且向它移動。由于螢火蟲算法依靠局部信息搜尋原理，使得螢火蟲算法很難深陷局部極值點，同時由于存在動態決策域，保證了魯棒性。因為螢火蟲都趨向于向位置最佳以及亮度最高的個體移動，而最佳個體為了尋找更佳的位置隨機移動，因此促使整個群體形成了一種正反饋，極大地提升了全局尋優能力，所以對于組合式參數(c,σ)的全局優化極其適用。

文獻[19]代表目前的研究成果，結合實驗發現基本的螢火蟲算法還是存在一些缺點的，即算法前期的收斂速度相對比較緩慢，后期因為其收斂不夠穩定以至于不能提升算法的精度。因為位置更新時段中的不變步長導致收斂不夠穩定以及收斂速度緩慢。不變步長使得前期的螢火蟲不能以最快的速度移向更亮的同伴，與此同時在后期隨著螢火蟲之間的位置越來越接近，亮度的差值也越來越小，起初的步長造成了螢火蟲不能進一步靠近最亮的那只螢火蟲的不穩定現象的產生，從而降低了基本螢火蟲算法的精度。針對上述缺點，利用FA算法中的位置更新原理[20-22]，并通過在螢火蟲移動時添加亮度特征，構成以下位置更新的公式:

(28)

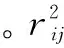
(29)

所要靠近的那只螢火蟲越亮，移動的步長越長，從而加快了前期的收斂速度，而在后期隨著螢火蟲之間的亮度越來越接近，也會縮短移動的步長，這樣就可以在最優的位置微調，防止產生收斂不穩定的現象。

4 實驗結果與分析

實驗采用的群體行為視頻都是用Canon EOS 70D單反相機在室外露天場地拍攝的，幀率為40 frame/ps，圖片大小為480×640。一共包括6種群體行為：gather(聚集)、chat(聊天)、split(分離)、linger(徘徊)、meet(相遇)、together(同行)，圖2表示6種群體行為的運動軌跡。圖中各目標都處在第一幀的起始位置，曲線表示各個目標的運動軌跡，利用協方差匹配算法進行目標跟蹤得到運動軌跡，曲線的終點位置表示各目標運動停止的位置，當有個別幀由于嚴重遮擋而造成目標丟失時，利用人工進行修正。

圖2 六種群體行為軌跡圖

樣本視頻如表1所示。實驗采用改進螢火蟲算法的支持向量機對群體行為進行分類，分類效果如圖3所示。

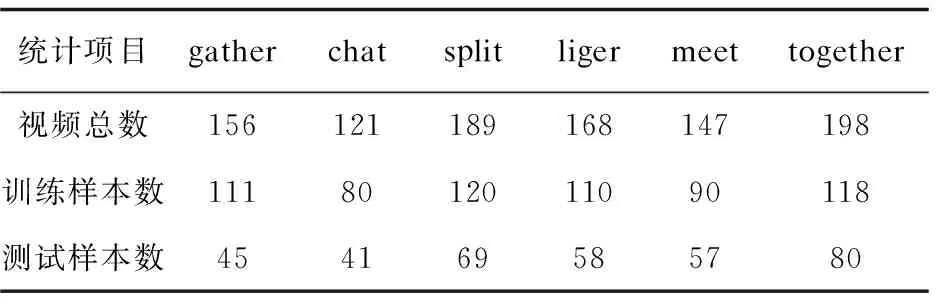
表1 視頻采集及實驗樣本數統計表

圖3 群體行為的識別率對比

從圖3可以看出，對于6種群體行為均是融合特征取得最好的識別率，而linger和together兩種行為的識別率相對較低，together行為利用融合特征得到的識別率為85%，而利用運動特征和外觀特征的識別率分別為72%和43%。而對于linger行為，利用融合特征得到的識別率為85%，而利用運動特征和外觀特征的識別率分別為68%和56%。同時，比較了利用未改進的支持向量機對融合特征進行分類，結果表明文中方法更優。

綜上所述，利用融合特征明顯比單純地利用運動特征和外觀特征的效果好，并且采用改進螢火蟲算法的支持向量機的分類效果要優于未改進的支持向量機。在這6種群體行為中，linger的識別率相對較低，那是由于linger行為具有較強的隨機性，在進行小片段分解群體行為視頻時，很容易影響其各段行為的一致性，所以識別率相對較低。

5 結束語

提出了一種基于融合特征的群體行為識別方法。利用運動軌跡，通過計算格蘭杰因果檢驗值，衡量各目標之間相互作用和影響的程度，同時將人群個體作為頂點，將個體間相互影響程度作為邊權重，構建群體復雜因果網絡，并結合外觀特征來分析群體行為，根據改進螢火蟲算法的支持向量機進行分類識別。該方法融合了運動信息和外觀信息來描述群體行為，從微觀層面利用目標運動軌跡構建群體復雜網絡，同時從宏觀層面對群體復雜網絡特性進行分析，以此在微觀層面和宏觀層面架起一個橋梁，為小規模群體行為識別開辟了一個新的想法。利用格蘭杰因果關系檢驗算法對目標之間的因果關聯度進行度量，同時以此量化網絡的邊的結構和權重，為群體因果復雜網絡的構建提供了基礎。改進螢火蟲算法的支持向量機,既保證了收斂性能，又提高了分類精度，優化效果顯著。

[1] ANDRADE E L,BLUNSDEN S,FISHER R B.Modelling crowd scenes for event detection[C]//International conference on pattern recognition.[s.l.]:IEEE,2006:175-178.

[2] GE W,COLLINS R T.Marked point processes for crowd counting[C]//IEEE conference on computer vision and pattern recognition.[s.l.]:IEEE,2009:2913-2920.

[3] KRATZ L,NISHINO K.Anomaly detection in extremely crowded scenes using spatio-temporal motion pattern models[C]//IEEE conference on computer vision and pattern recognition.[s.l.]:IEEE,2009:1446-1453.

[4] 胡 波,李曉華,沈蘭蓀.場景監控中的人群密度估計[J].電路與系統學報,2007,12(6):19-22.

[5] XIONG G,CHENG J,WU X,et al.An energy model approach to people counting for abnormal crowd behavior detection[J].Neurocomputing,2012,83(7):121-135.

[6] 金 標,胡文龍,王宏琦.基于時空語義信息的視頻運動目標交互行為識別方法[J].光學學報,2012,32(5):145-151.

[7] 梁 敏,劉貴喜.基于自適應混合濾波的多目標跟蹤算法[J].光學學報,2010,30(9):2554-2561.

[8] 王澤兵,楊 衛,秦 麗.基于粒子群算法的動態熱釋電目標跟蹤[J].光學學報,2014,34(10):27-33.

[9] TU P,SEBASTIAN T,DORETTO G,et al.Unified crowd segmentation[C]//European conference on computer vision.Marseille,France:[s.n.],2008:691-704.

[10] BLUNSDEN S,FISHER R B.Pre-fight detection-classification of fighting situations using hierarchical AdaBoost[C]//Proceedings of the fourth international conference on computer vision theory and applications.[s.l.]:[s.n.],2009:303-308.

[11] GUO P,MIAO Z.Action detection in crowded videos using masks[C]//20th international conference on pattern recognition.[s.l.]:IEEE,2010:1767-1770.

[12] 胡芝蘭,江 帆,王貴錦,等.基于運動方向的異常行為檢測[J].自動化學報,2008,34(11):1348-1357.

[13] ZHU G,YAN S,HAN T X,et al.Generative group activity analysis with quaternion descriptor[M]//Advances in multimedia modeling.Berlin:Springer,2011.

[14] DORE A,REGAZZONI C S.Interaction analysis with a Bayesian trajectory model[J].IEEE Intelligent Systems,2010,25(3):32-40.

[15] CHU H,LIN W,WU J,et al.A new heat-map-based algorithm for human group activity recognition[C]//Proceedings of the 20th ACM international conference on multimedia.[s.l.]:ACM,2012:1069-1072.

[16] KHAN S M,SHAH M.Detecting group activities using rigidity of formation[C]//ACM international conference on multimedia.Singapore:ACM,2005:403-406.

[17] F?RSTNER W,MOONEN B.A metric for covariance matrices[M]//Geodesy-the challenge of the 3rd millennium.Berlin:Springer,2000:299-309.

[18] ZHOU Y,NI B,YAN S,et al.Recognizing pair-activities by causality analysis[J].ACM Transactions on Intelligent Systems & Technology,2011,2(1):389-396.

[19] 黃正新,周永權.變步長自適應螢火蟲群多模態函數優化算法[J].計算機工程與應用,2012,48(8):43-47.

[20] YANG X S.Firefly algorithms for multimodal optimization[J].Mathematics,2009,5792:169-178.

[21] 劉長平,葉春明.一種新穎的仿生群智能優化算法:螢火蟲算法[J].計算機應用研究,2011,28(9):3295-3297.

[22] YANG X S.Nature-inspired metaheuristic algorithms[M].[s.l.]:Luniver Press,2010.