Finite-time Synchronization of Memristor-based Neural Networks with Discontinuous Activations

WANG Yan-qun，HOU Juan

(College of Mathematics and Statistics,Hengyang Normal University,Hengyang Hunan 421002)

In 1971,memristor (an abbreviation for memory resistor),as the fourth basic circuit element along with the resistor,capacitor and inductor,was firstly proposed by Leon O.Chua[1].Almost 40 years later,the Hewlett-Packard (HP) research team successfully fabricated a solid state implementation of the memristor and showed that a memristor is a nonlinear circuit element and its value,called memristance or memductance,is not unique with an official publication in Nature[2-3].Since the memristor has memory and behaviors more like biological synapses,we can replace the resistors in neural networks by memristors,so memristor-based neural networks (MNNs) are conceived.Since Pecora and Carroll[4]proposed a drive-response scheme for synchronization of coupled chaotic systems,much attention has been paid to synchronization in view to its wide potential applications in secure communication,biological informations,and so on.Recently,many results on synchronization of MNNs are available in the literature,see reference[5-8].

However,most of the above mentioned results on synchronization of MNNs were based on the assumption that the activation functions are continuous even global Lipschitz.But in practice it is known that MNNs with discontinuous activations might be better candidates in designing and implementing an artificial neural networks.

Motivated by the above discussions,in this paper we discuss the finite-time synchronization problem for a class of MNNs with discontinuous neuron activations by differential inclusion theorems.

1 Preliminaries

In this paper，we consider a class of MNNs with discontinuous activation functions described by the following equation

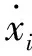
(1)

wherei∈l={1,2,…,n},n≥2 denotes the number of neurons in the neural networks;xi(t) corresponds to the voltage of the capacitorCi;fj(·)is the feedback function;Iidenotes the external bias on theith unit;di(·) andaij(·)are the memristor-based weights given by

WhereMijdenotes the memductances of memristorsWij.Wijrepresents the memristor between the feedback functionfj(xj(t))andxi(t),Rirepresents the parallel-resistor corresponding to the capacitorCi.

As is well known,capacitorCiis invariant while memductances of memristorsMijandWij,respond to change in pinched hysteresis loops.Consequently,di(xi)andaij(xi)will change.According to the feature of memristor and the current-voltage charateristics,we apply a general mathematical model of the memristance as follows:

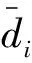
Now,we introduce the following definitions about set-valued map and differential inclusion[9].

Definition1.LetE?Rn,x|F(x)is called a set-valued map fromE|Rn,if for eachx∈E,there corresponds a nonempty setF(x)?Rn.A set-value mapFwith nonempty values is said to be upper semi-continuous atx0∈E?Rnif,for any open setNcontainingF(x0),there exists a neighborhoodMofx0such thatF(M)?N.F(x)is said to have a closed (convex,compact) image if for eachx∈E,F(x)is closed (convex,compact).

Throught out this paper,for the model (1),we introduce the following assumptions:

A2:For eachi,there exist a nonnegative constantsLiandNisuch that

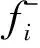
A3:The activation functionfjare bounded.That is,for anyj∈l,there exists real numbersMjsuch that

|fj(v)|Mj,forallv∈R.

Definition2A functionx:[0,L)→Rn,L∈(0,+],is called a state solution of (1)on [0,L)if

(i)xis continuous on [0,L)and absolutely continuous on [0,L);

(2)

Any functionηsatisfying (2) is called an output solution associated to the statex.With this definition it turns out that the statexis a solution of (1) in the sense of Filippov since it satisfies

(3)

for a.e.t≥0,i∈l.

Consider the neural network model (1) as the driver system,the controlled response system can bedescribed as follows:

(4)

Similarly

(5)

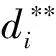
(6)

2 Synchronize in finite time

In the proof of the main results we shall need the following lemmas.

Lemma1(ChainRule)[10]Suppose thatV(z):Rn|RisC-regular,and thatz(t):[0,+)|Ris absolutely continuous on any compact interval of [0,+).Then,V(z(t)):[0,+)|Ris differential for a.e.t∈[0,+),and we have

(t),?ξ∈?V(z(t)).

Lemma2Let Ωi(xi,yi)=-sign(yi-xi)(K[di(yi)]yi-K[di(xi)]xi)fori∈l,wherexiandyi∈R.Then for anyωi(xi,yi)∈Ωi(xi,yi),the following inequality is satisfied

ωi(xi,yi)

Lemma3[11]Suppose thatV(z(t)):Rn|RisC-regular,and thaz(t):[0,+)|Rnis absolutely continuous on any compact interval of [0,+).If there exists a continuous functionα(t):[0,+)|Rwithα(σ)>0 forσ∈(0,+),such that

(t)-α(V(t))

and

then we haveV(t)=0 fort≥T.In particular,ifα(σ)=kσβandk>0,then the settling timeTis estimated by

In the following,we are to investigate the synchronization of system (1)and (4).Letei(t)=yi(t)-xi(t)fori∈l,and designing the controllerui(t)in the response system (6) as follows:

ui(t)=-kiei(t)-qisign(ei(t)),i∈l,

(7)

wherekiandqifori∈lare control gains .Therefore,the error dynamics system of (1) and (6) can be expressed by the following form

(8)

and

Based on the discontinuous controller (7),the following result can be derived.

Theorem1.Suppose A1,A2,A3 hold,if the response system (4) is control with the control (7) andki,qiare arbitrary positive constant determined later.Then the response network (4) can be synchronized with the drive network (1) in a finite time

(9)

Proof.Construct the following Lypunov functional:

(10)

Calculating the derivative ofV(t),from lemma1 we get

-kiei(t)-qisign(ei(t))].

From lemma 2,one has

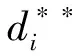
In addition,from the assumption A2 and A3 we have

Introducing above two inequalities to the derivative ofV(t) and applying the inequalitya2+b2≥2ab,we have

Choosingkiandqilarge enough such that

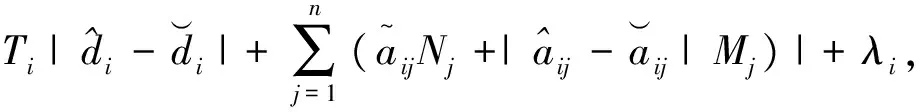
whereλi>0 fori∈lis arbitrarily chosen constant.

Letλ=mini∈l{λi}>0,then one has

[1] CHUA L O.Memristor-The missing circuit element[J].IEEE Transactions on Circuit Theory CT,1971,18:507-519.

[2] STRUKOV D B,SNIDER G S,STEWART D R,et al.The missing memristor found[J].Nature 2008,453:80-83.

[3] TOUR J M,HE.T.The fourth element[J].Nature,2008,453:42-43.

[4] GUO Z Y,WANG J,YAN.Z.Global expoential disspativity and stabilization of memristor-based recurrent neural networks with time-varying delays[J].Neural Networks,2013,18:158-172.

[5] CHEN J J,ZENG Z G,JIANG.P.Global Mittag-Leffler stability and synchronization of memristor-based fractional-order neural networks[J].Neural Networks,2014,51:1-8.

[6] SAKTHIVEL R,ANBUVITHYA R,MATHIYALAGAN K,et al.Reliable anti-synchronization conditions for BAM memristive neural networks with different memductance functions[J].Applied Mathematics and Computation,2016,275:213-228.

[7] ABDURAHMAN A,JIANG H J,TENG.Z.D.Exponential lag synchronization for memristor-based neural networks with mixed time delays via hybrid switching control[J].Journal of the Franklin Institute,2016,353:2859-2880

[8] ABDURAHMAN A.JIANG H J,TENG.Z.D.Finite-time synchronization for memristor-based neural networks with time-varying delays[J].Neural Networks,2015,69:20-28.

[9] FILIPPOV A.F.Differential equations with discontinuous righthand sides.Boston[M].MA: Kluwer Academic Publishers,1988.

[10] HUANG L,GUO Z.Global convergence of periodic solution of neuralnetworks with discontinuous activation functions.Chaos[J].Solitons and Fractals,2009,42:2351-2356.

[11] LIU X,PARK J H,JIANG N J,et al.Nonsmooth finite-time stabilization of neural networks with discontinuous actvations[J].Neural Networks,2014,52:25-32.

(編校 陳志陽)