基于Simulink的伺服缸新型支撐結構控制系統仿真研究

馬強俊，黃慶學,2，馬麗楠，和東平

(1.太原科技大學 重型機械教育部工程研究中心，太原 030024；2.太原理工大學 機械工程學院，太原 030024)

大型重載伺服液壓缸是伺服控制系統的關鍵元件，也是液壓滾切剪機的核心設備，其性能的好壞嚴重影響著伺服缸的使用壽命以及滾切剪機的生產效率[1-3]。在滾切剪機上，伺服缸需臥式鉸接安裝，輸出曲線力，旋轉一定的角度，但是，由于缸筒自身重力的影響，會引起拉缸、泄漏以及輸出力減小等不良反映，為了解決這些問題，提出一種在伺服缸端底鉸接一個支撐小缸的新型支撐結構以及配套的外接液壓控制系統。該控制系統是新型支撐結構的核心，可以精確控制支撐小缸的壓力和位移，使其保證伺服缸的活塞桿全程無摩擦運行，進而改善伺服缸性能，以滿足實際工況。

目前，國內外許多學者在壓力和位置同步精確控制研究方面取得了顯著成就[4-7]。MADANI et al[8]在外科手術中使用的醫療機械手，WELLS et al[9]在視網膜顯微手術過程中的手持式機器人等方面成功實現了壓力與位置的同步精確控制。謝苗等[10]提出的電液伺服位置與壓力復合控制方法，王君等[11]提出的位置壓力主從伺服控制系統，權龍等[12]提出的位置閉環在外，壓力閉環在內的串并聯復合控制策略等方法有效的提高了壓力與位置同步控制的精確度與穩定性。

基于以上研究背景，本文設計了一種壓力、位置雙閉環獨立PID控制系統，可以精確控制支撐小缸的壓力和位移，使其保證伺服缸的活塞桿全程無摩擦運行，避免了由于伺服缸自身重量所引起的密封圈摩損、拉缸和泄漏等現象。通過對壓力、位置控制系統耦合特性的分析和研究，進行解耦運算，推導出該系統的數學模型，并進行系統穩定性分析。運用MATLAB/Simulink進行控制仿真，驗證該控制系統的可行性與可靠性，為新型支撐結構的工程應用提供了扎實的基礎。

1 新型結構控制原理

滾切剪機上臥式鉸接安裝的伺服缸在做工時，需輸出曲線力并旋轉一定的角度，針對這種工況，本文提出了一種在伺服缸端底鉸接一個支撐小缸的新型結構，并配套了該結構的控制系統。通過對支撐小缸壓力、位置的精確控制，實現了伺服缸活塞桿全程無摩擦運行，其工作原理如圖1所示。

1-伺服缸；2-支撐小液壓缸；3-比例換向閥；4-比例溢流閥；5-控制器；6-液壓泵；7-聯軸器；8-電動機；9-壓力傳感器；10-位移傳感器圖1 新型結構控制原理圖Fig.1 Schematic diagram of new structure control

該伺服控制系統通過對壓力和位置的自適應調整，使伺服缸的活塞桿始終懸浮在缸蓋導向套中，實現全程無摩擦運行，避免由于缸筒自身重量所引起的拉缸、泄漏以及輸出力不足等現象。通過控制器對壓力和位移傳感器的反饋數據進行及時處理，分別實時控制比例溢流閥與比例換向閥，對支撐小缸的輸出力及位置進行精確控制，從而控制活塞桿始終懸浮在缸蓋導向套中，避免由于伺服缸缸筒自身重量引起的不利影響，達到一個動態平衡。

2 模型建立與穩定性分析

2.1 控制系統的耦合關系

根據控制系統原理可知，壓力、位置雙閉環系統存在著一定的耦合特性，使得壓力、位置難以獨立控制，因此需要進行解耦。通過對控制系統原理的分析，得到如圖2的耦合系統框圖。

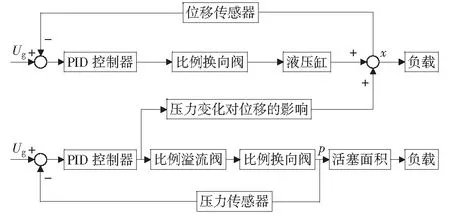
圖2 壓力位置耦合關系框圖Fig.2 Coupling relation of pressure and position

壓力閉環控制系統是通過支撐小缸無桿腔的壓力傳感器將檢測到的壓力信號與給定信號反饋給PID控制器，實時控制比例溢流閥，通過比例換向閥壓降后，使其輸出給定力。位置閉環控制系統是通過位移傳感器將檢測到的位移信號與給定信號反饋給PID控制器，實時控制比例換向閥，使其輸出適量的液壓流量來控制液壓缸活塞桿的位移，與此同時，壓力的變化也會對位移造成一定的影響。

2.2 建立數學模型

比例溢流閥是壓力閉環控制系統的核心元件，其數學模型比較復雜，為了便于分析研究，將其簡化為二階系統模型[13]。

(1)

式中：ω1為比例溢流閥固有頻率，ξ1為比例溢流閥阻尼比。

由于活塞桿伸出與縮回運動類似，下面只做活塞桿伸出階段的比例換向閥壓降計算。

(2)

式中：Δp為比例換向閥總壓降；ps為進油壓力；p1為無桿腔壓力；p2為有桿腔壓力；Q1、Q2分別為比例換向閥進、出油流量；a1、a2分別為進、回閥口開啟面積。

由一些相互關系可得：

(3)

式中:A1為無桿腔有效面積；A2為有桿腔有效面積；k為進、回閥口開啟面積比值。

由式(2)、式(3)得:

(4)

由力平衡得：

p1A1=p2A2+F.

(5)

式中：F為外負載力。

由式(4)、式(5)得：

p1=k1ps+k2F.

(6)

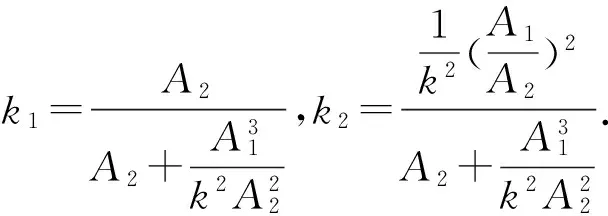
令p2=0，則得比例換向閥壓降比例環節：

p1=k3ps.

(7)

比例換向閥是位置閉環控制系統的核心元件，其模型十分復雜，為了便于分析研究，將其簡化為二階系統模型[14]。

(8)

式中：kq為流量增益，ω2為比例換向閥固有頻率，ξ2為比例換向閥阻尼比。

閥控缸位移的數學模型比較復雜，為了便于分析，將其簡化為[15]：

(9)

式中：ωh為液壓缸的固有頻率，ξh液壓缸的阻尼比。

壓力變化對位移的影響，根據力平衡公式可得：

(10)

通過對式(10)進行拉氏變化可得：

(11)

由以上的分析可以得到如圖3所示的雙輸入雙輸出系統耦合框圖。

圖3 系統耦合框圖Fig.3 System coupling diagram

圖中GPID1(s)為位置閉環PID控制器，GPID2(s)為壓力閉環PID控制器。

位置閉環的控制對象傳遞函數為：

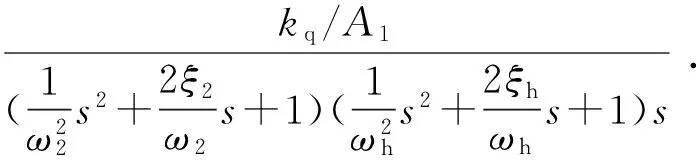
(12)

壓力變化對位移的影響的傳遞函數為：

(13)

壓力閉環的控制對象傳遞函數為：

(14)

2.3 解耦運算

本文采用前饋解耦來解除多變量系統的耦合性，簡化解耦控制系統框圖如圖4.

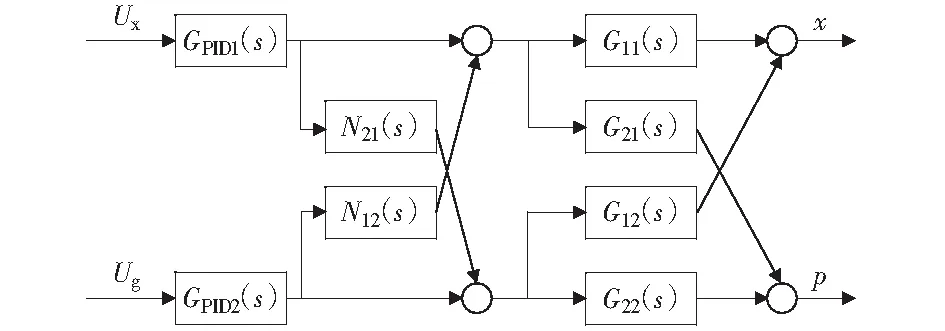
圖4 簡化解耦控制系統框圖Fig.4 Decoupling control system diagram

其中N(s)為解耦裝置矩陣，由簡化解耦控制系統可得：

(15)

由于解耦矩陣須為對角矩陣，則：

(16)

由式(15)、(16)可得解耦矩陣模型為：

(17)

解耦后的廣義對象模型為：

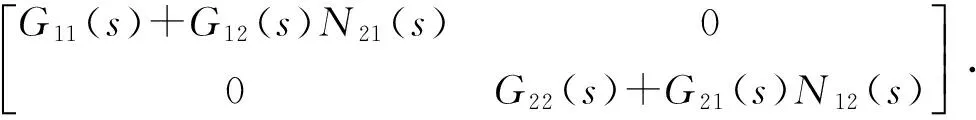
(18)

通過對位置閉環控制系統分析與研究，可知比例換向閥的固定頻率ω2=2.1 rad/s，比例換向閥的阻尼比ξ2=0.7，液壓缸的固定頻率ωh=370 rad/s，液壓缸的阻尼比ξh=0.2，無桿腔的有效面積A1=0.007 85 m2，流量增益kq=0.037.將其代入式(12)得：

(19)

通過對壓力變化對位移的影響的分析和研究，可知m=11 kg，Bp=2×105kg/s.將其代入式(13)得：

(20)

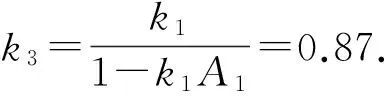
(21)

由式(17)—(21)可得：

(22)

(23)

2.4 穩定性分析

由以上解耦運算可得到壓力和位置獨立閉環的控制對象線性化模型，運用李雅普諾夫第二法對壓力和位置閉環分別進行穩定性分析。通過對控制系統的研究可知壓力傳感器增益kp=0.42，位移傳感器增益kx=0.2.

壓力閉環控制系統傳遞函數為：

(24)

由傳遞函數可以得壓力閉環控制系統的自治方程為：

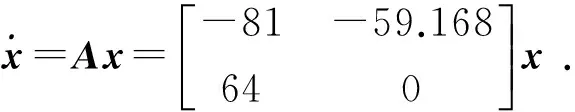
(25)

取正定二次函數V(x)=xTHx作為可能的李雅普諾夫函數，則：

(26)

只要ATH+HA正定，就可以判定系統是大范圍漸進穩定的。令

ATH+HA=-E.

(27)

式中：E為單位矩陣。

只要判定H為正定矩陣，就可以得到ATH+HA為正定，設判定矩陣

(28)

通過計算可得：

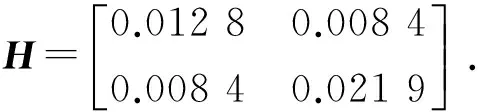
(29)

由式(29)可知是H正定矩陣，因此可得該壓力閉環控制系統為穩定系統。

位置閉環控制系統傳遞函數為：

(30)

同樣，采用李雅普諾夫第二法對其進行穩定性分析，得判定矩陣：

(31)

由于D是正定矩陣，因此可得該位置閉環控制系統為穩定系統。

3 控制仿真

為了進一步驗證該控制系統的合理性和穩定性，運用MATLAB/Simulink進行仿真控制，在Simulink上搭建壓力閉環與位置閉環的控制仿真模型如圖5、圖6所示。

圖5 壓力閉環控制仿真Fig.5 Simulation of pressure closed loop control

圖6 位置閉環控制仿真Fig.6 Simulation of position closed loop control

為了驗證該控制系統的跟蹤性能以及抗干擾能力，在0 s時給予壓力閉環控制系統與位置閉環控制系統單位階躍信號，并在4 s時加入幅值為0.1的階躍干擾信號。壓力閉環控制系統的PID值分別為：2.1，0.02，0；位置閉環控制系統的PID值分別為：2，0.2，0.01，其仿真結果如圖7、圖8所示。

通過圖7和圖8可以看出，壓力信號與位置信號跟蹤性能良好，抗干擾能力強。由壓力階躍信號響應圖7的局部放大圖可以看到，在壓力上升的瞬間產生微小振蕩，在0.1 s后跟蹤給定值，同樣在4 s時加入干擾信號時，0.1 s后跟蹤給定值，壓力閉環控制系統實現了快速穩定跟蹤給定值。由位置階躍信號響應圖8可以看出，位置信號可以快速無超調的達到跟蹤給定值，在4 s時加入干擾后，很快能夠跟蹤到給定值。該仿真結果驗證了壓力、位置雙閉環獨立PID控制系統的合理性與可靠性。

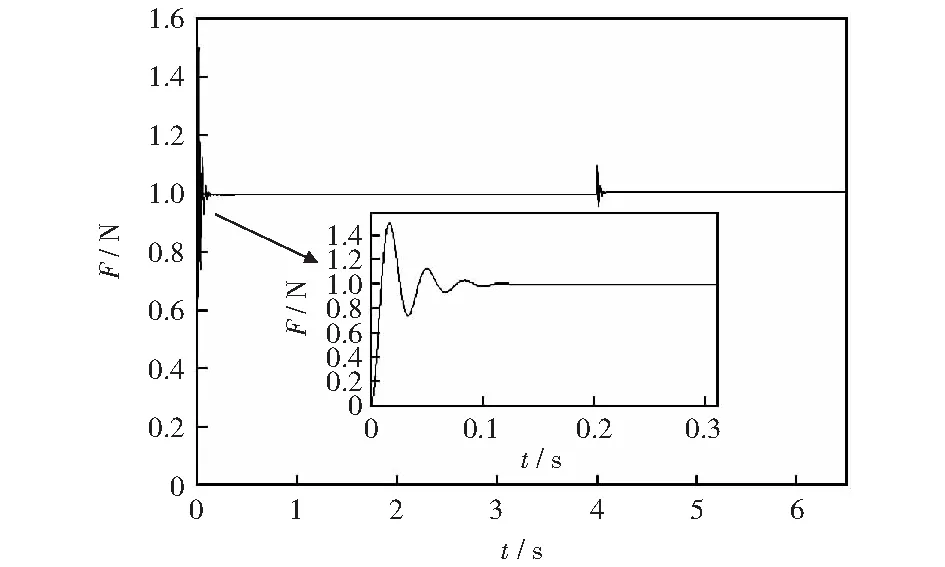
圖7 壓力階躍信號響應圖Fig.7 Response diagram of pressure step signal

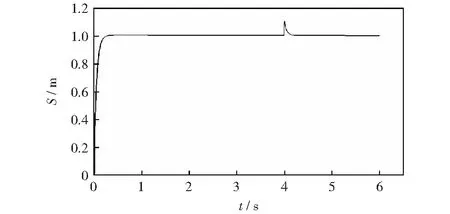
圖8 位置階躍信號響應圖Fig.8 Response diagram of position step signal

4 實驗驗證

為了驗證壓力、位置雙閉環獨立PID控制系統的可行性與可靠性，搭建試驗臺，并對規格為?100/80-250的支撐小缸作為執行機構的液壓控制系統進行現場測試。其中比例溢流閥型號為RZMO-P1ES-PS-010/315/1，比例換向閥型號為4WRDE16-125L-5X/6L24K9/M，液壓泵的型號為EOS4VSO125OR/30R-PPB13U34，排量為125 mL/r，伺服缸的規格為?360/220-400，壓力傳感器型號為HDA3840-A-400-000，位移傳感器的型號為RHM0420MD701S2G1102.

通過對新型結構的動力學研究，可知活塞桿往返全程運行8.4 s，前4 s為勻速伸出階段，4 s后為勻速返程階段，小缸的輸出力曲線模型為：

(32)

式中：F為給定輸出力函數曲線；s為給定位移函數曲線；G、m1分別為臥式伺服缸缸筒重量、質量；a為缸筒質點的切向加速度；θ為臥式缸的旋轉角。

通過現場測試，結果得到如圖9、圖10所示。

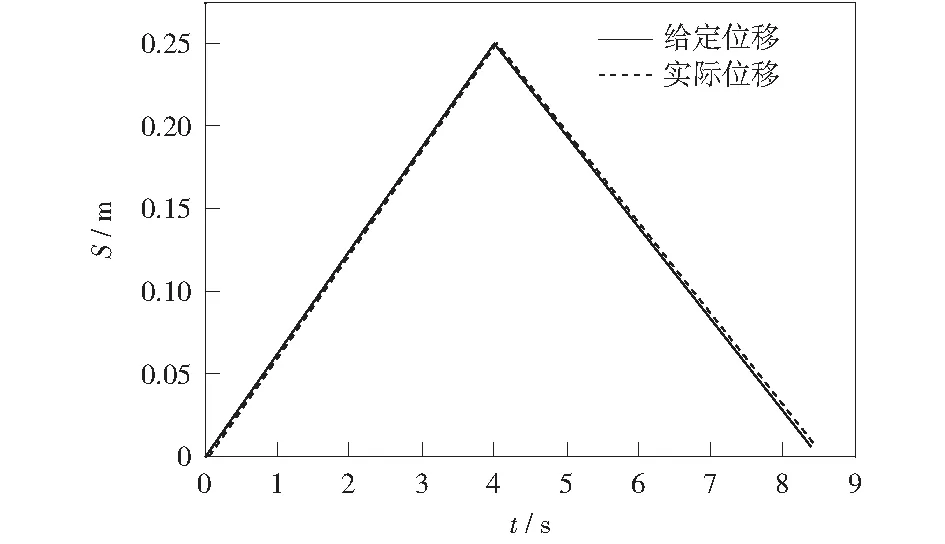
圖9 位移測試結果圖Fig.9 Results of displacement test

根據位移測試結果圖9可以看出，位置控制系統基本實現了快速穩定跟蹤給定信號，其誤差在0.004 m以內，達到了新型結構位置精確跟蹤的工況需求。通過輸出力測試結果圖10可以看到，在前4 s的活塞桿在伸出階段，實際輸出力穩定跟蹤給定值，達到了工況需求。在4 s后的活塞桿返程階段，由于有桿腔壓力變大，導致無桿腔背壓增大，使實際輸出力變大，其誤差在3.8%以內，這是預測范圍之內的，對實驗結果不會造成影響。

圖10 輸出力測試結果圖Fig.10 Results of output force test

通過實驗驗證了壓力、位置雙閉環獨立PID控制系統的可行性與可靠性，實現了力與位置獨立控制，為伺服缸端底鉸接一個支撐小液壓缸的新型結構提供了可靠的現實依據。

5 結論

由仿真試驗結果可以看出，基于伺服缸端底鉸接一個支撐小缸的新型結構的壓力、位置雙閉環獨立PID控制系統設計是可行的，可以實現小缸壓力與位置同步精確控制，使伺服缸活塞桿全程無摩擦運行，其誤差在可以接受的范圍之內。通過在伺服缸端底鉸接一個支撐小缸的新型結構及其控制系統，有效的改善了滾切剪機伺服缸的工況，為解決類似問題提供了一定的依據，具有較高的應用價值。

[1] 馬立峰,黃慶學,韓賀永,等.驅動復合連桿機構滾動的液壓控制系統特性[J].北京工業大學學報,2012,38(11):1601-1607.

MA L F,HUANG Q X,HAN H Y,et al.Characteristics of hydraulic control system for using driving the composite connecting rod mechanism Rolling[J].Journal of Beijing University of Technology,2012,38(11):1601-1607.

[2] 楚志兵,黃慶學,馬立峰,等.滾切式雙邊剪連桿機構的動力學仿真及實驗研究[J].四川大學學報(工程科學版),2011,43(1):247-252.

CHU Z B,HUANG Q X,MA L F,et al.Experimental study and simulation of kinetics on linkage structure of rolling-cut bilateral shear[J].Journal of Sichuan University (Engineering Science Edition),2011,43(1):247-252.

[3] JIAN F M,WEI Z W,YING Z L.Experimental and theoretical investigation on the sealing performance of the combined seals for reciprocating rod[J].Journal of Mechanical Science and Technology,2012,26(6) :1765-1772.

[4] YAO J,LI B,KONG X D,et al.Displacement and dual-pressure compound control for fast forging hydraulic system[J].Journal of Mechanical Science and Technology,2016,30(1):353-363.

[5] JUN J P,JIN X,POTT A,et al.Hybrid position/force control using an admittance control scheme in Cartesian space for a 3-DOF planar cable-driven parallel robot[J].International Journal of Control,Automation and Systems,2016,14(4):1106-1113.

[6] 高炳微,邵俊鵬,韓桂華.電液伺服系統位置和力模糊切換控制方法[J].電機與控制學報,2014,18(5):99-104.

GAO B W,SHAO J P,HAN G H.Fuzzy switching control between position and force for electro-hydraulic servo system[J].Electric Machines and Control,2014,18(5):99-104.

[7] YANOU A,MINAMI M,TANIMOTO H.Continuous shape-grinding experiment based on model-independent force/position hybrid control method with on-line spline approximation[J].Artificial Life and Robotics,2013,18(3/4):219-227.

[8] MADANI M,MOALLEN M.Hybrid position/force control of a flexible parallel manipulator[J].Journal of the Franklin Institute,2011,348(6):999-1012.

[9] WELLS T S,YANG S,MACLACHLAN RA,et al.Hybrid position/force control of an active handheld micromanipulator for membrane peeling[J].Int J Med Robot,2016,12(1):85-95.

[10] 謝苗,劉治翔,池城,等.巷道超前支架的電液伺服位置壓力復合控制方法[J].中國機械工程,2016,27(2):239- 245.

XIE M,LIU Z X,CHI C,et al.Electro-hydraulic servo position and pressure hybrid control method of fore poling system on tunneling[J].China Mechanical Engineering,2016,27(2):239-245.

[11] 王君,黃慶學,安高成,等.液壓滾切剪機位置壓力主從控制的研究[J].流體傳動與控制,2015(5):5-10.

WANG J,HUANG Q X,AN G C,et al.Research on position-pressure master-slave control of rolling shear hydraulic system[J].Fluid Power Transmission & Control,2015(5):5-10.

[12] 權龍,許小慶,李敏,等.電液伺服位置、壓力復合控制原理的仿真及試驗[J].機械工程學報,2008,44(9):100-105.

QUAN L,XU X Q,LI M,et al.Simulation and test electro-hydraulic servo position and pressure hybrid control principle[J].Journal of Mechanical Engineering,2008,44(9):100-105.

[13] 王傳禮,丁凡,殷建立,等.卷染機電液張力控制系統的動態特性研究[J].浙江大學學報(工學版),2004,38(5):631-635.

WANG C L,DING F,YIN J L,et al.Reseach on dynamic characteristics of jigger electro-hydraulic tension control system[J].Journal of Zhejiang University (Engineering Science),2004,38(5):631-635.

[14] 李勝,阮健,孟彬.二維電液比例換向閥動態特性及穩定性分析[J].機械工程學報,2016,52(2):202-212.

LI S,RUAN J,MENG B.Two-dimensional electro-hydraulic proporti onal directional valve[J].Journal of Mechanical Engineering,2016,52(2):202-212.

[15] 陳柏金,徐明昊,張紅穎.液壓鍛造操作機大車行走機構的位置控制系統[J].華中科技大學學報(自然科學版),2011,39(8):7-9.

CHEN B J,XU M H,ZHANG H Y.Position control system for hydraulic forging manipulator cart movement mechanism[J].Journal of Huazhong University of Science and Technology(Natural Science Edition),2011,39(8):7-9.