基于正弦激勵的WASD神經網絡的上證指數預測

馬 川， 廖柏林， 周 俊， 周元玲， 毛凱文

0 引言

證券市場是一個充滿魅力的市場，每位投資者都想從證券交易中獲取高額利潤.但是，證券市場是一個典型的具有隨機性、時變、波動性較大的非線性系統，難以建立精確的數學模型.多年來，人們一直在尋找有效方法以實現對證券市場的精確預測[1-3].許多學者采用傳統回歸分析和時間序列方法對證券市場進行了預測和分析，通過證券價格的歷史時間序列挖掘其變化趨勢[4-7].然而這些傳統方法并不能描述實際證券市場的非線性情況，其預測結果也不理想.20世紀80年代以來，神經網絡算法得到了快速發展和廣泛應用[8-11].由于神經網絡具有自組織、自學習能力，不需要考慮數學模型的內部結構，可以對非線性系統進行無限逼近和擬合，為證券市場預測和分析的深入研究開拓了新的空間[12-13].常有的神經網絡預測方法有BP神經網絡、SVM和小波網絡等.但由于每種網絡模型本身的問題，使得其效果不佳.權值與結構直接確定（WASD）的神經網絡作為一種新型的前向神經網絡，通過偽逆直接確定網絡權值，減少了迭代過程，避免了訓練速度慢、過擬合、局部極值等缺陷，具有訓練速度快，全局最優和泛化能力優異等特點[14-18].針對上證指數預測問題，本文提出了一種多輸入單輸出、正弦激勵的WASD神經網絡模型，并對該模型的權值和結構確定方法進行了理論分析.最后，我們利用1991年12月20日至2016年10月12日的數據對WASD神經網絡進行訓練，并對其后10天的上證指數進行預測.將本文預測結果與現有的BP神經網絡和SVM神經網絡的預測結果進行對比，結果顯示本文所提的正弦激勵的WASD神經網絡具有更好的預測性能.

1 正弦激勵的WASD神經網絡模型

本文采用的WASD神經網絡是一種三層前向神經網絡，其模型如圖1所示.使用單極性正弦函數作為激勵函數，輸入層神經元閥值為0，輸入層神經元到隱含層神經元的連接權值w∈[χ1，ζ1]和隱含層神經元的閥值β∈[χ2，ζ2]，χ1，ζ1，χ2，ζ2 取值可相同也可不相同.在輸入層神經元到隱含層神經元連接權值確定的條件下，隱含層神經元到輸出層神經元連接權值通過偽逆直接一步算出.

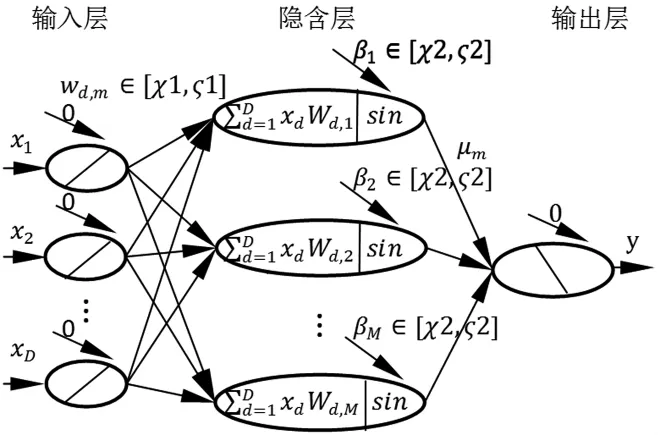
圖1 正弦激勵的WASD神經網絡模型

1.1 權值直接確定方法

輸入層神經元到隱含層神經元的權值和隱含層的閥值通過隨機確定，其隨機范圍常通過試錯法確定.第n個輸入在第m個隱含層的輸出為hm，n，hm，n通過以下公式計算

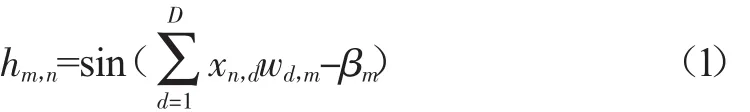
所有的輸入通過公式（1）計算得到矩陣H，如下

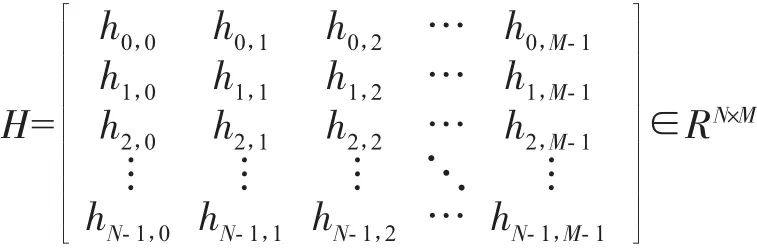
其中N為樣本數，M為隱含層神經元數.

隱含層到輸出層神經元的連接權值μ可以通過公式（2）一步直接確定

其中H+為矩陣H的偽逆，δ為學習目標樣本所構成的列向量.

1.2 結構直接確定方法

本文設定誤差為E，其確定方式如式（3）

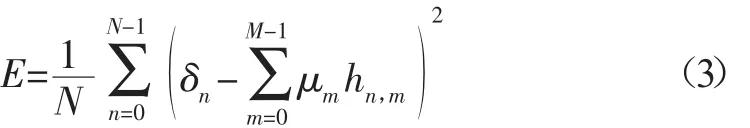
其中δn為第n天上證指數開盤的實際值，μm為第m隱層神經元到輸出層的連接權值.

為了提高神經網絡的穩定性和防止過擬合現象的發生，我們在引入加權誤差Etol，在神經網絡學習同時進行內部校驗，并按照式（3）計算得到學習誤差Etra以及內部校驗誤差Evol.通過（4）式計算出加權誤差Etol

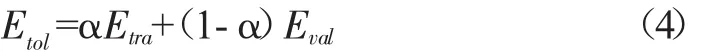
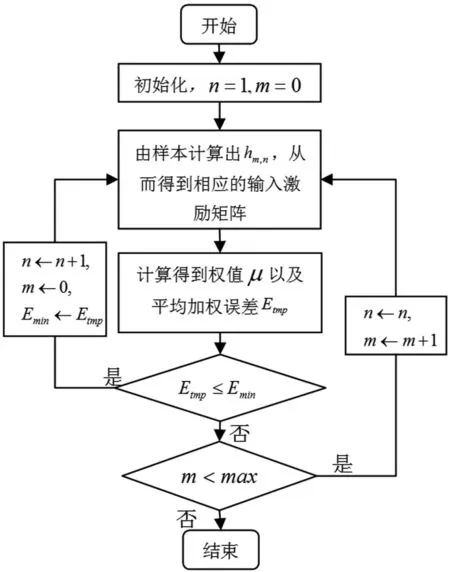
圖2 權值與結構確定算法流程圖

并將加權誤差Etol用于后續神經網絡最優結構的確定.其中，α為用于學習的樣本數在整個訓練樣本中所占的比例.

對于網絡的結構，我們使用邊增邊刪原則.以加權誤差Etol為增刪神經元標準，并設定最大的重置次數max.先逐個增加隱含層神經元，當Etol不再下降時，重置新增的神經元（即重新給定該神經元的閥值以及輸入層到隱含層的連接權值），如果更換次數達到max（設定的最大重置次數）次仍不能使Etol下降，則停止，此即為最優的WASD神經網絡預測結構.具體流程圖如圖2所示.

2 上證指數預測實驗

本文采用了1990.12.20-2016.10.12期間內6 312個交易日每日上證綜合指數的6種指標（開盤價、收盤價、最高價、最低價、成交量和成交金額）用于訓練，并對2016年10月12日后面10個工作日的上證指數進行預測（本文數據來源于http：//quotes.money.163.com/trade/lsjysj_zhishu_000001.html）.其中我們設置訓練中的最大重置次數max=10、100、1000，用于討論max的設定對網絡預測精度和穩定性的影響.然后我們在常采用的6種指標的基礎上進行加減指標來確定哪些指標是最有使用價值的指標，使正弦激勵的WASD神經網絡的性能發揮到極致.

將原始數據進行歸一化，使得數據分布在[-1，1]區間內，取消各維度數量級差別，避免應輸入輸出數量級差異太大而造成網絡預測誤差較大和網絡的不穩定性.在使用時，將數據進行反歸一化.

本文將訓練數據中前5 812個數據用來學習，后500個用來內部校驗（即α=5812/6312）.在訓練時，按照（3）式和（4）式同時計算出學習誤差、校驗誤差和加權誤差.我們以加權誤差為判斷標準，每次增加一個神經元，直到加權誤差增大時重置該隱含層神經元.待重置次數大于預先設定的重置次數max式，仍然大于前面的誤差時，訓練結束.在整個訓練中，各誤差隨著隱含層神經元個數的增加而變化情況展示在圖3中.圖中，我們展現的是最大重置次數max=1000時的情況，可以觀察到通過逐個添加隱藏層神經元，加權誤差先下降，然后開始上升，在轉折點（即，隱含層神經元個數等于28個）處即為正弦激勵的WASD神經網絡的最優結構.因此，最優結構為隱含層神經元個數等于28個.

在實驗時，我們發現最大重置次數的設置對我們預測的精度和穩定性有很大的影響.為此，我們對其進行了探討.我們將最大重置次數max分別設置為10次、100次和1 000次進行實驗，同時對后面的10天進行了預測，并按（3）式計算出它們的誤差.為了避免偶然誤差，我們對每類實驗重復進行了5次，并記錄了相關實驗數據，由于篇幅有限，本文將5次數據進行了平均處理，其數據見表1.

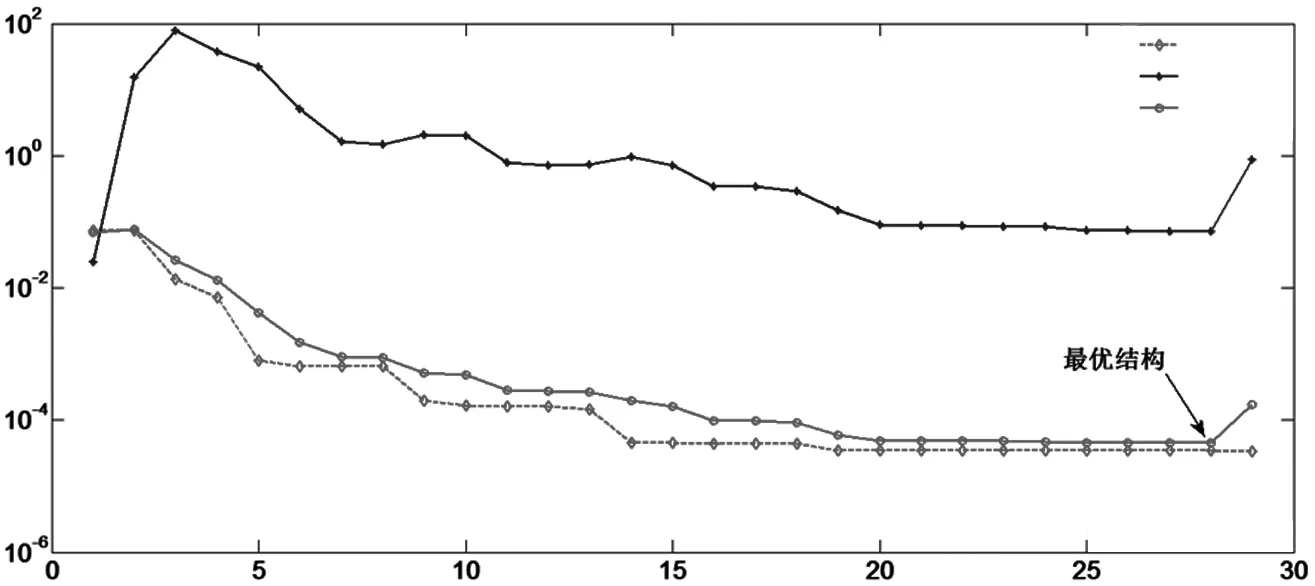
圖3 隱含層神經元個數和各誤差的關系

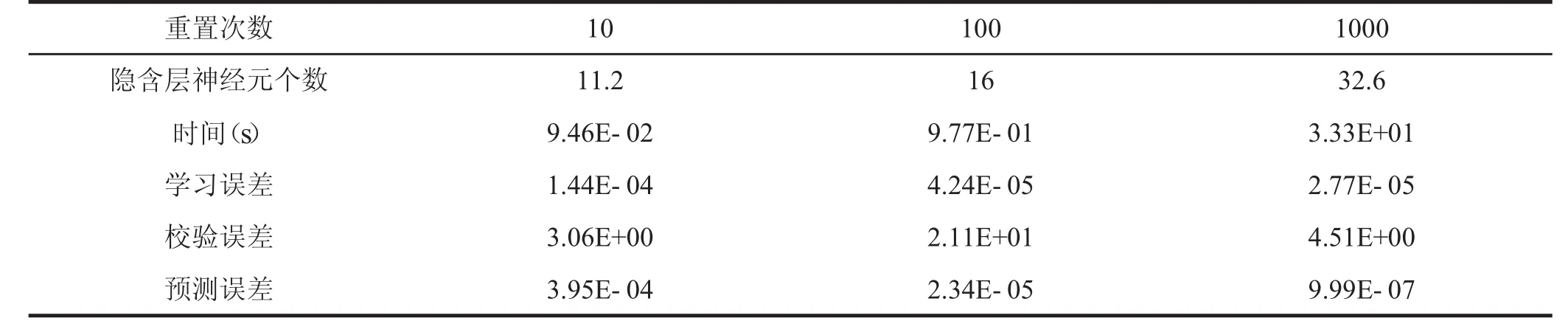
表1 WASD神經網絡性能和重置次數的關系

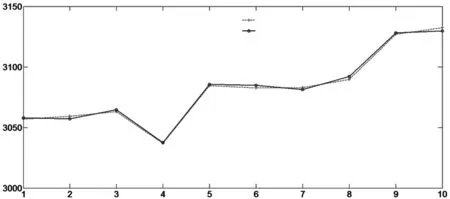
圖4 正弦激勵的WASD神經網絡的預測結果

從表1我們可以得出：隨著重置次數的增加，隱含層神經元的個數也隨之增加，而預測誤差呈數量級的減小.由此也可得出，前面隨機設置的w和β這兩個參數對網絡性能的影響也在減小.但值得指出的是，重置次數增加，訓練時間也將增加，為此我們需根據實際需要合理選擇重置次數，本文采用的重置次數max=1000.圖4為采用6種指標作為輸入，正弦激勵的WASD神經網絡對上證指數的預測結果.

從圖4可以看出預測結果與實際值基本重合，由此可知預測結果非常準確.為了更直觀的看出預測結果與實際值的差異，我們定義預測的絕對誤差為

Actual_E=yn-δn（5）

其中yn為第n天的預測值.我們將這10天的絕對誤差展示在圖5中.從圖5可以看出正弦激勵的WASD神經網絡預測的絕對誤差Actual_E在3以內，進一步說明了本文所提神經網絡的預測精度非常高.

對上證指數的預測時所用的輸入變量一般使用開盤價、收盤價、最高價、最低價、成交量和成交金額這6個指標.但是，上證指數的指標不僅僅只有6種，實際上共有9種數據.為了驗證和避免因訓練時使用的輸入變量個數和類型的不準確而造成預測結果的不精確，我們在常規6種數據的基礎上進行了增刪.然后分別進行了實驗，為了減少和避免偶然誤差，我們對每類實驗重復進行了5次.由于篇幅限，我們在對數據進行了平均處理，并將結果展示在表2中.

通過表2，我們可以發現不同的輸入類型，其預測精度和訓練時間都不同.預測精度最高的為輸入類型1和2，而最差的為輸入類型6.此外，輸入類型1的訓練時間最短.這也表明了本文所采用的數據輸入類型的正確性.

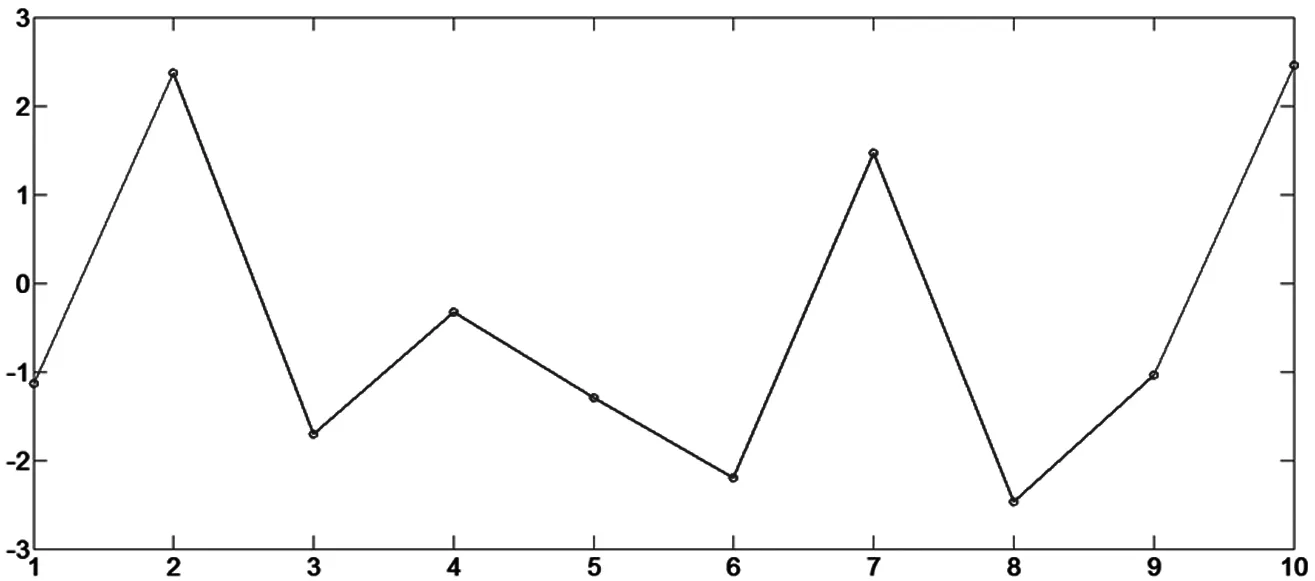
圖5 正弦激勵的WASD神經網絡預測的實際誤差

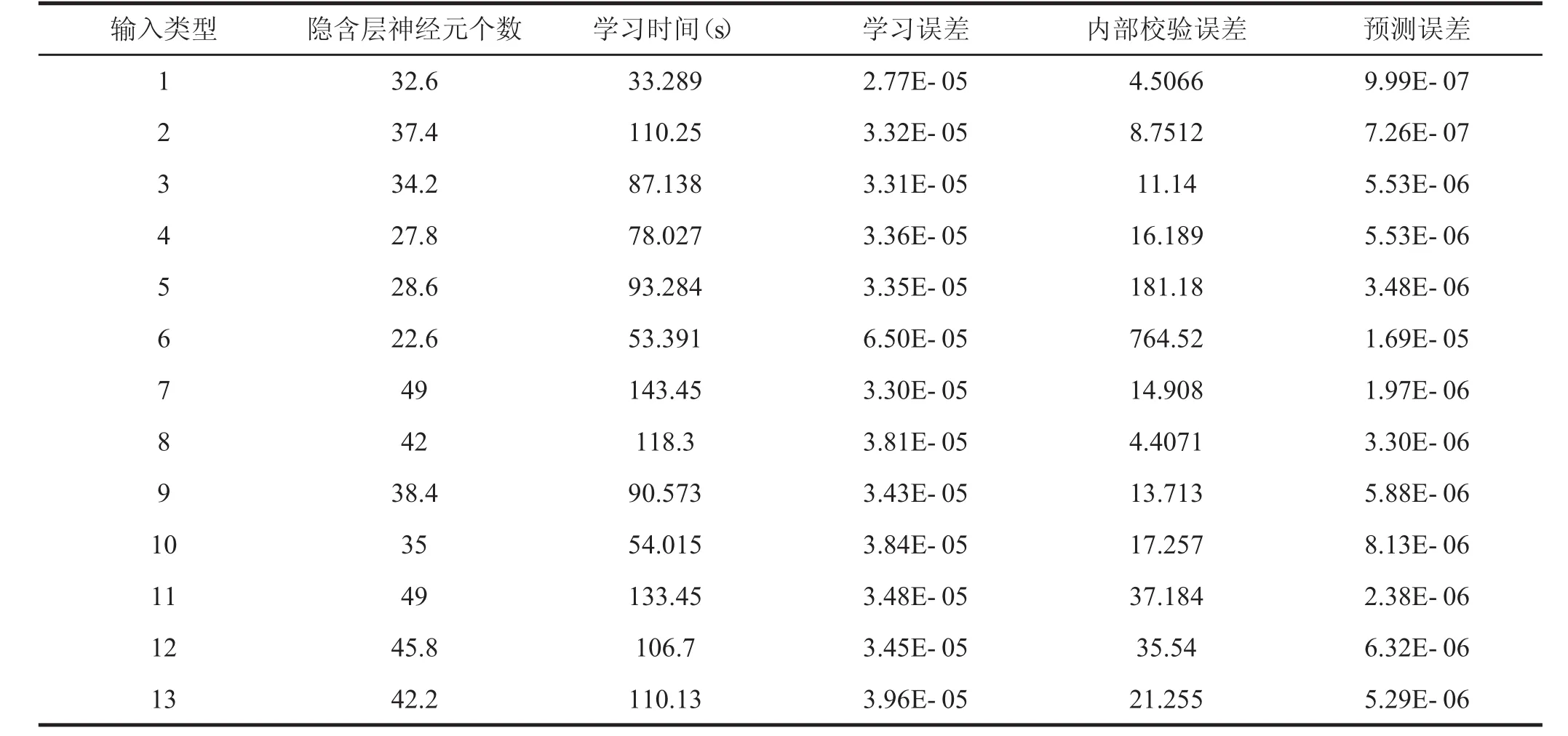
表2 WASD神經網絡性能和不同輸入類型的關系

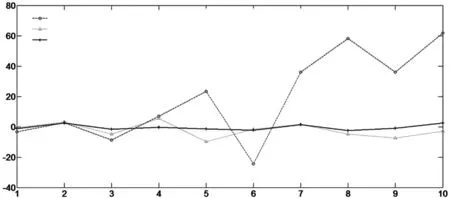
圖6 正弦激勵的WASD、BP和SVM預測的實際誤差對比結果

為了進一步說明正弦激勵的WASD神經網絡在上證指數預測中的優勢，我們將其與BP神經網絡和SVM兩種傳統預測方法進行了對比.為了更加直觀的展示，我們給出它們預測的實際誤差圖，如圖6所示.

從圖6可以看出，相比BP和SVM神經網絡，正弦激勵的WASD神經網絡預測的絕對誤差最小，也即其具有最好的預測精度.

3 結論

WASD神經網絡是一種新型前向神經網絡，通過權值與結構直接確定，減少了復雜的迭代過程.計算機數值實驗結果表明：構建的正弦函數激勵的WASD神經網絡能有效地實現其最優權值與最優結構的自確定，且此神經網絡在上證指數應用中具有十分優越的擬合.另外，本文通過對比正弦函數激勵的WASD神經網絡與BP和SVM在上證指數預測應用上的性能差異，證實了正弦函數激勵的WASD神經網絡在非線性程度增加時具備更為優越的學習性能，這也展現了正弦函數激勵的WASD神經網絡在數據挖掘等方面的應用潛力和前景.

[1]胡杉杉，黨佳瑞，藍柏雄.中國證券市場的可預測性研究[J].財經科學，2001（3）：35-39.

[2]楊一文，劉貴忠.基于神經網絡的多變量時間序列預測及其在股市中的應用[J].信息與控制，2001，30（5）：413-417.

[3]周廣旭.一種新的時間序列分析算法及其在股票預測中的應用[J].計算機應用，2005，25（9）：2179-2184.

[4]顧嘉運，劉晉飛，陳明.基于SVM的大樣本數據回歸預測改進算法[J].計算機工程，2014，40（1）：161-166.

[5]譚顯勝，周鐵軍.BP算法改進方法的研究進展[J].懷化學院學報，2006，25（2）：126-130.

[6]南敬昌，田娜.基于改進粒子群算法的模糊小波神經網絡建模[J].計算機工程與應用：2017，5（33）：120-123.

[7]李軍，黃杰.基于自組織映射神經網絡的局部自回歸方法在網絡流量預測中的應用 [J].信息與控制，2016，45（1）：120-128.

[8]鐘海全，李穎川，劉永輝，等.基于BP神經網絡的多相管流模型優選及應用分析[J].中國科技論文在線，2008，（11）：873-878.

[9]田亞鵬，鞠斌山.基于遺傳算法改進BP神經網絡的頁巖氣產量遞減預測模型[J].中國科技論文，2016，11（15）：1710-1715.

[10]黃宏運，吳禮斌，李詩爭.BP神經網絡在股票指數預測中的應用[J].通化師范學院學報，2016，37（10）：32-34.

[11]汪思成，肖林，嚴慧玲.基于不同誤差函數的神經網絡求解線性方程組[J].吉首大學學報（自然科學版），2016，37（6）：26-28.

[12]陳海英.基于支持向量機的上證指數預測和分析[J].計算機仿真，2013，30（1）：297-300.

[13]Liao BL，Zhang Y N，Jin L.Taylor O（h3）discretization of ZNN models for dynamic equality-constrained quadratic programming with application to manipu-lators [J].IEEE Transactions on Neural Networks and Learning Systems，2016，27（2）：225-237.

[14]Li S，Li Y M.Nonlinearly activated neural network for solving time-varying complex Sylvester equation[J].IEEE Transactions on Cybernetics，2013，44（8）：1397-1407.

[15]Jin L，Zhang Y N，Li S.Integration-enhanced Zhang neural network for real-time-varying matrix inversion in the presence of various kinds of noises[J].IEEE transactions on neural networks and learning systems，2016，27（12）：2615-2627.

[16]Zhang Y N，Guo D S，Luo Z Y，et al.CP-activated WASD neuronet approach to Asian population predic-tion with abundant experimental verification [J].Neu-rocomputing：2016，198：48-57.

[17]Zhang Y N，Yin Y H，Guo D S，et al.Cross-validation based weights and structure determination of Cheby-shev-polynomial neural networks for pattern classifica-tion[J].Pattern Recognition，2014，47（10）：3414-3428.

[18]Zhang Y N，Yu X T，Guo D S，et al.Weights and struc-ture determination of multiple-input feed-forward neural network activated by Chebyshev polynomials of class 2 via crossvalidation[J].Neural Computing and Applications，2014，25（7-8）：1761-1770.