基于兩相流理論錯齒式迷宮密封的數值研究

周春平 ，張 雨

（1.成都工業職業技術學院 軌道交通工程系，四川 成都 610218；2.西南交通大學 牽引動力國家重點實驗室，四川 成都 610031）

1 引言

迷宮密封是一條介質通過時產生盡可能高流阻以保持較小泄漏為目的的流體通道。迷宮密封避免了密封件之間的相互摩擦，不需要潤滑，具有結構簡單、允許熱膨脹變形、性能安全可靠等優點。但是，迷宮密封自身結構特點決定了介質泄漏不可避免，只能通過優化密封結構來提高密封性能[1]。

高速動車齒輪箱作為驅動系統的核心部件，其可靠性直接影響列車運行的動力性能和安全性能。齒輪箱高速運行時，潤滑油易從車軸與端蓋的間隙中泄漏，不能產生良好的潤滑和冷卻效果，影響齒輪箱安全高效的使用。齒輪箱密封系統采用軸向密封與徑向密封相結合，其中，軸向密封采用直通式迷宮密封或錯齒式迷宮密封，對于惡劣運行工況，多采用錯齒式迷宮密封。

國內外學者采用熱力學理論、計算流體力學等方法分析迷宮密封的密封特性。基于不可壓縮理想氣體介質和熱力學理想模型，國內外學者給出多種迷宮密封泄漏量計算方法，構造多種計算公式：文獻[2-4]這些公式通過理論推導，引入密封系數，進行多組試驗分析，選取合理的密封系數，忽略密封具體的幾何結構，因此，特定結構對應特定密封系數，公式的指導意義有限。對于迷宮密封的數值研究，文獻[5-7]數值研究了直通式迷宮密封的空腔參數、轉速、壓比等因素對迷宮密封性能的影響。文獻[8-9]基于CFD軟件分析錯齒式迷宮密封的密封機理，基于單介質分析密封結構對密封性能的影響，得到錯齒式迷宮密封具有空腔耗散效應強、透氣效應弱等優點的結論。

目前，迷宮密封以單相理想氣體為研究對象，在實際工程應用中，高速動車齒輪箱內齒輪高速旋轉、攪拌潤滑油，箱體內部形成高溫高壓的物理環境，潤滑油破裂、霧化并與內部空氣充分混合，最終以油霧-空氣混合物形式進入密封系統。因此，論文基于油霧-空氣兩相介質研究錯齒式迷宮密封性能，分析油霧參數對迷宮密封性能的影響，為錯齒式迷宮密封的設計提供理論參考。

2 數值模擬分析

2.1 兩相流模型

兩相流模型主要包括Mixture模型、VOF模型和DPM模型，對于齒輪箱內部潤滑油充分攪拌，形成與空氣均勻混合的流體介質進入密封系統，不考慮油霧冷凝為液態潤滑油的物態變化過程，選用兩相之間耦合關系較強的Mixture模型，求解油-氣混合相的連續性方程、動量方程和能量方程。

齒輪箱采用BASF Emgard Rw_A 75W_90潤滑油，當齒輪箱運行一段時間后，箱體內部溫度場、壓力場趨于穩定波動，潤滑油霧化并與空氣充分混合。仿真分析時，混合兩相流以空氣為主相，油霧為次相，且兩相均無相變反應。根據粘溫公式[11]，100℃時液態潤滑油密度為816kg/m3,動力粘度為0.0135Pa·s,潤滑油油霧密度設為9.4kg/m3,動力粘度設為5e-5Pa·s。

2.2 數學模型

迷宮密封內部油氣混合物的流動過程可認為是穩態湍流流動，采用可壓縮流的雷諾平均Navier-Stokes方程與k-ε湍流模型進行數值仿真。

根據質量守恒方程、動量守恒方程和能量守恒方程，得到數值模擬通用方程的微分形式[10]：

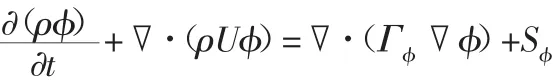
式中：φ—通用變量；U—速度矢量；ρ—油-氣混合密度；Γφ—擴散系數；Sφ—源相。當φ取不同值時，通用方程分別代表質量守恒方程、各方向的動量方程和能量守恒方程。

徑向迷宮密封仿真時湍流模型選用RNG k-ε模型，RNG kε模型考慮湍流漩渦，能夠以較高精度計算流線彎曲程度較大的徑向迷宮內部流場。

RNG k-ε湍流模型的湍流能k和湍流能耗散率ε的方程分別為：

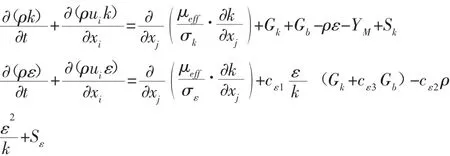
式中：Gk—平均速度梯度引起的湍動能；Gb—浮力引起的湍動能；YM—可壓縮流的脈動擴張；cε1、cε2、cε3—常數；σk、σε—k、ε 的Prandtl數；μeff—有效粘度，μeff=μ+μt，μ—流體的動力黏性系數，μt—湍動粘度；Sk、Sε—源相。

2.3 計算模型

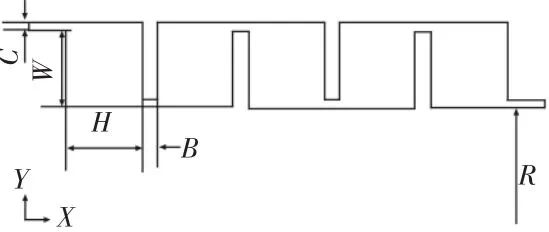
圖1 錯齒式迷宮密封計算模型Fig.1 Calculation Model of the Interlocking Labyrinth Seal

研究油霧參數對錯齒式迷宮密封的影響，只考慮密封介質的軸向和徑向運動，結構中介質運動簡化為二維運動。五腔錯齒式迷宮密封的計算模型圖，如圖1所示。密封間隙寬度C=1 mm，空腔寬度W=10 mm，，空腔高度H=10 mm，節流齒齒厚B=2 mm，轉子半徑R為75mm。

錯齒式迷宮密封左端為壓力入口，給定總壓和總溫300 K，出口邊界設為壓力出口，出口壓力為環境背壓，進出口壓比取（1.2～1.8）。壁面取無滑移、無滲透邊界條件，且按絕熱壁面處理，轉子壁面繞X軸旋轉，由于轉子轉速對迷宮密封性能影響可忽略不計[11]，轉速取2000r/min。油霧顆粒直徑取（1～20）μm，混合相中油霧體積分數為（1～20）%，且考慮重力作用。為了保證計算精度，采用有限體積法離散控制方程，離散格式均采用二階迎風格式離散，并采用隱式耦合求解方法。求解收斂的標準為連續方程、速度、湍動能及耗散率的殘差小于10-3，能量方程的殘差小于10-6，進出口質量流量不平衡率小于0.1%。

3 仿真驗證

3.1 網格無關性驗證

錯齒式迷宮密封幾何模型規則，可采用非結構化網格進行劃分，壁面采用標準壁面函數，無需對近壁面區域進行網格加密處理。為減少網格大小導致的計算誤差，保證計算精度的同時考慮計算效率，對網格尺寸進行無關性驗證。

網格尺寸分別取（0.05～0.125）mm進行計算，網格數量為（77880～480086），得到壓比為 1.4、油霧直徑為 10μm、油霧濃度為10%時密封油霧泄漏量為（79.68～82.32）g/s，相差不超過5%，滿足網格無關性要求。綜合考慮計算精度和計算效率，選節點尺寸為0.10 mm進行計算分析。

3.2 仿真方法驗證

油霧-空氣兩相介質的迷宮密封沒有合適的試驗對比，為了驗證仿真方法的正確性，參考經典迷宮密封試驗，對試驗結構進行分析，對比仿真結果與試驗數據，論證仿真方法的可靠。

文獻[12]中給出了直通式迷宮密封試驗模型和數據，文獻中采用密封系數CD作為密封性能無量綱值，密封系數CD表達式如下：

式中：mmeans—試驗或數值計算得到的介質泄漏量；mid—等熵理論計算介質泄漏量；A—間隙面積；P0、Pn—入口、出口壓力；T0—介質初始溫度；R—理想氣體常數；k—理想氣體等熵指數。

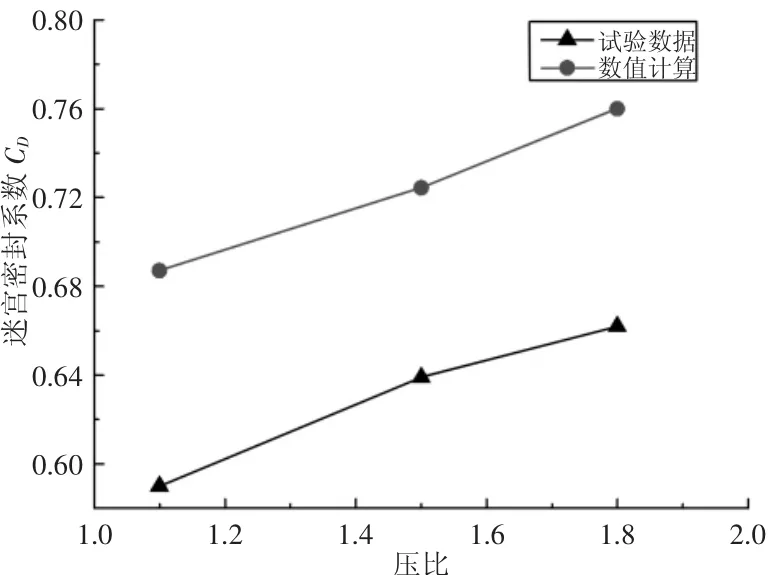
圖2 數值計算與試驗數據對比圖Fig.2 Comparison of Numerical Calculation and Experimental Data

迷宮結構參數詳見文獻[12]，轉子壁面轉速取1000r/min，轉子半徑75mm，介質為理想氣體，進出口壓比取（1.1～1.9），得到不同壓比下密封系數曲線對比圖，如圖2所示。由圖可知，數值計算與試驗數據變化規律一致，同一壓比下，誤差不超過20%，與文獻[13]所得結果較一致，滿足工程實踐的要求，認為仿真方法可行。

4 錯齒式迷宮密封內部流場分析

運用Fluent軟件對錯齒式迷宮密封流場進行數值分析，邊界條件設置為進出口壓比1.4，油霧顆粒直徑10μm，油霧體積分數為10%，仿真得到迷宮密封內壓力云圖，如圖3所示。迷宮密封混合介質的速度矢量圖，如圖4所示。

圖3 錯齒式迷宮密封壓力云圖Fig.3 Pressure Contour of the Interlocking Labyrinth Seal

圖4 錯齒式迷宮密封速度矢量圖Fig.4 Velocity Vector Maps of the Interlocking Labyrinth Seal

由圖3、圖4可知，迷宮壓力逐腔遞減，在空腔的邊角區域形成較大壓力梯度；流體介質在通過節流齒時產生降壓增速，由于節流齒和壁面作用，在密封間隙區域形成拋射流，介質速度達到最大，壓力降低；密封空腔中形成明顯的渦流，符合密封空腔耗能效應，將密封內部壓力通過渦流運動轉化為熱能進行耗散，實現壓力降低；空腔中渦流中心區域流速較低，壁面中心區域流速較大，邊角區域由于空腔結構限制和渦流形狀影響，形成無流體或少流體的“死區”，壓力梯度較大。

圖5 錯齒式迷宮密封密度分布云圖Fig.5 Mixture Density Contour of the Interlocking Labyrinth Seal

錯齒式迷宮密封的介質密度云圖，如圖5所示。由云圖可知，內部流場中充滿油霧-空氣混合介質，云圖中密度最小值為空氣密度1.225kg/m3，最大值為油霧密度9.4kg/m3。密封空腔中中心區域密度較小，外部區域密度較大，表明油霧顆粒主要集中于渦流的外側區域，這是由于密封空腔中混合介質形成強旋轉氣流，使得混合介質受到較大的渦流離心力，密度較大的油霧顆粒分布于渦流的外側，油霧顆粒運動形式為沿壁面流動。沿壁運動有利于油霧顆粒的凝聚，通過設置回油孔等措施可有效減少密封系統中油霧的泄漏。錯齒式迷宮密封的密封性能不僅受到節流齒節流效應、空腔耗散效應、沿程摩擦阻力效應作用，同時也受到渦流離心力作用的影響。因此，需要基于油霧-空氣兩相介質和空腔中渦流離心力作用分析錯齒式迷宮的密封性能。

5 油霧參數對迷宮密封性能的影響

油霧作為密封系統主要的密封介質，其相關參數直接影響密封系統的密封性能。以油霧顆粒直徑和顆粒濃度（體積參數）為研究對象，分析油霧參數對密封系統中介質泄漏量的影響。

5.1 油霧顆粒直徑

為了研究油霧顆粒直徑對錯齒式迷宮密封性能的影響，設置進出口壓比為（1.2～1.8），油霧顆粒直徑為（1～20）μm，油霧體積分數為10%，分析得到不同壓比下油霧顆粒直徑與錯齒式迷宮密封泄漏量關系曲線圖，如圖6所示。

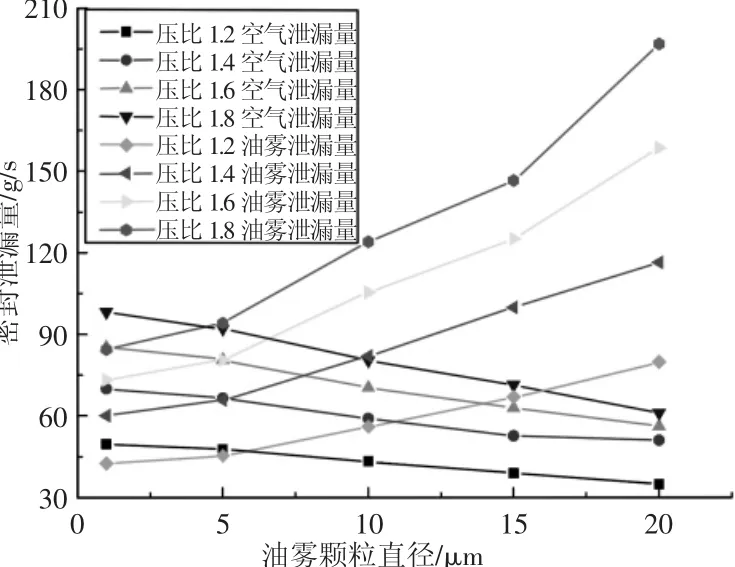
圖6 油霧顆粒直徑與泄漏量關系曲線Fig.6 The Curve of Oil Vapor Diameter on Leakage Loss

由圖6可知，隨著油霧顆粒直徑的增大，油霧泄漏量增加，空氣泄漏量減少，隨著進出口壓比增加，油霧、空氣泄漏量以近似線性方式增加。進出口壓比不變，油霧直徑增加，入口混合介質中油霧體積分數一致，流入錯齒式迷宮密封中油霧質量一定，油霧數量減少，單個油霧顆粒質量增大。錯齒式密封結構不變且入口壓力相同，空腔內部形成的渦流強度基本一致，油霧顆粒質量越大，渦流離心力越大，油霧顆粒易分布于渦流邊緣區域，油霧顆粒沿壁面流動，造成油霧泄漏量越大。油霧顆粒直徑不變，進出口壓力越大，空腔中渦流強度增強，渦流邊緣的流速越大，油霧顆粒承受的渦流離心力越大，造成油霧泄漏量的增加。

5.2 油霧顆粒濃度

錯齒式迷宮密封內部介質是油霧-空氣混合介質，因此油霧顆粒濃度直接影響迷宮密封的密封性能。仿真設置進出口壓比為（1.2～1.8），油霧顆粒直徑為 10μm，油霧體積分數為（1～20）%，分析得到不同壓比下油霧濃度（體積分數）與錯齒式迷宮密封泄漏量關系曲線圖，如圖7所示。

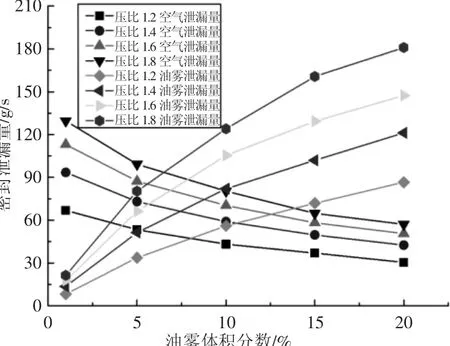
圖7 油霧體積分數與泄漏量關系曲線Fig.7 The Curve of Oil Vapor Volume Fraction on Leakage Loss

由圖7可知，隨著油霧體積分數增加，油霧濃度增大，油霧泄漏量增加，空氣泄漏量減小，隨著進出口壓比增加，油霧泄漏量增加，濃度越大，壓比對油霧泄漏量影響越大。進出口壓比一定時，油霧體積分數越大，進入密封結構中潤滑油越多，渦流離心力作用導致油霧顆粒分散于渦流區外側，更多油霧顆粒沿壁面運動造成油霧泄漏量增加。當油霧體積分數一定時，進出口壓比越大，渦流強度越大，渦流離心力增強，造成油霧泄漏增加，油霧濃度越大時，渦流離心作用對油霧泄漏量影響越明顯。

6 結論

基于油-氣混合兩相流理論對錯齒式迷宮密封的內部流場和密封性能進行分析，分析了油霧參數對密封性能的影響。通過分析，得到以下結論：（1）影響錯齒式迷宮密封的密封性能的因素不僅有密封結構導致的節流齒效應、空腔耗散效應、沿程摩擦阻力效應，也需要考慮渦流離心力作用。（2）渦流產生的離心力使得油霧顆粒沿壁面運動。油霧顆粒直徑越大，濃度越高，壁面運動越強，油霧泄漏量越大，空氣泄漏量減小。（3）油霧顆粒沿壁面運動有利于顆粒之間的凝聚，可通過回油孔的合理設置，減少油霧的泄漏。根據研究結果，在合理設計錯齒式迷宮密封時，需要考慮空腔內部渦流離心力的影響，通過設置回油孔等手段，可有效減少潤滑油的泄漏。

［1］張雨.高速動車齒輪箱內部流場與密封系統的數值研究［D］.成都：西南交通大學，2016（4）.（Zhang Yu.Numerical analysis of flow filed and labyrinth seal for highspeed train gearbox［D］.Cheng Du：Southwest Jiaotong University，2016（4）.）

［2］H M Martin.Labyrinth Packing［J］.Engineering，Jan.10.1908：35-36.

［3］A Egli.The Leakage of Steam Through Labyrinth Seals［J］.Transaction of ASME，1935（57）：115-122.

［4］李志剛，李軍，豐鎮平.蜂窩密封流動特性的數值研究和泄漏量公式的構造［J］.機械工程學報，2011，47（2）：142-148.（Li Zhi-gang，Li Jun，Feng Zhen-ping.Numerical investigation on discharge behavior and predication formula establishment of leakage flow rate of honeycomb seal［J］.Journal of Mechanical Engineering，2011，47（2）：142-148.

［5］W Zhao，T K Nielsen，J T Billdal.Effects of cavity on leakage loss in straight-through labyrinth seals.earth and environmental science［C］.25th IAHR Symposium on Hydraulic Machinery and Systems，Timisoara，Romanja，2010.IOP publishing，2010：1-8.

［6］Sivakumar Subramanian，A S Sekhar，B V S Prasad.Influence of combined radial location and growth on the leakage performance of a rotating labyrinth gas turbine seal［J］.Journal of Mechanical Science and Technology，2015，29（6）：2535-2545.

［7］G A Bondarenko，V N Baga，I A Bashlak.Flow simulation in a labyrinth seal［J］.Mechanics and Materials，2014（630）：234-239.

［8］Wang Wei-Zhe，Liu Ying-Zheng.Numerical analysis of leakage flow through two labyrinth seal［J］.Journal of Hydrodynamics，2007，19（1）：107-112.

［9］王琰，王麗娜，張開林.高速齒輪箱迷宮密封流場和泄露特性的數值研究［J］.內燃機車，2012，3（3）：6-9.（Wang Yan，Wang Li-na，Zhang Kai-lin.Numerical study of flow field and leakage characteristics of labyrinth seal for high speed gearbox［J］.Diesel Locomotives，2012，3（3）：6-9.）

［10］溫詩鑄，黃平.摩檫學原理［M］.北京：清華大學出版社，2002：9-10.（Wen Shi-zhu，Huang Ping.Principles of Tribology［M］.Beijing，Tsinghua University Press，2002：9-10.）

［11］張雨，張開林，姚遠.轉子轉速對迷宮密封性能影響的數值研究［J］.機械設計與制造，2017，3（3）：183-185.（Zhang Yu，Zhang Kai-lin，Yao Yuan.Numerical analysis of the rotor speed effect on labyrinth seal characteristics［J］.Machinery Design&Manufacture，2017，3（3）：183-185.）

［12］S.Witting，U.Schelling，S.Kim.Numerical predications and measurements of discharge coefficients in labyrinth seals［C］.International Gas Turbine Conference and Exhibition，Anaheim，California，1987.ASME publishing，GT 1987-188.

［13］Tong Seop Kim，Kyu Sang Cha.Comparative analysis of leakage seal configuration on leakage behavior［J］.Journal of Mechanical Science and Technology，2009，23（5）：2830-2838.