三維壓電微動平臺的結構設計與實驗測試

岳 強 ，劉文翠 ，張 研

（1.浙江紡織服裝職業技術學院 機電與軌道交通學院，浙江 寧波 315211；2.遷安首信自動化信息技術有限公司，河北 遷安064400；3.浙江紡織服裝職業技術學院 雅戈爾商學院，浙江 寧波 315211）

1 引言

隨著技術的進步和科技的發展，微/納米在各個工程領域的迅猛發展，人類社會的發展基本步入了納米時代，微納米技術擴展到各個領域。在微納米技術中，最常見的機構就是微動平臺，它是一種行程小、精度高、分辨率高的微動機構。如：在精密與超精密機械切削加工中，微動平臺可以應用為微進給或誤差補償裝置，實現刀具的微納米進給或加工誤差的精密補償[1]；在MEMS中，微動平臺配合微動夾鉗相用于微米乃至納米級機械零件的裝配或維修[2]；在掃描探針顯微鏡中，微動平臺與微探針、微夾鉗配合使用，用于進行樣品表面形貌測量，以及對原子內部進行分離操作或移植[3]。

鑒于微動平臺的諸多特點，需要多多借鑒微動平臺的優點，如文獻[4]研制的x-y-θ微動平臺，該平臺采用柔性薄板結構，通過壓電執行器驅動配合電磁夾緊機構實現蠕動式進給，可獲得了3個自由度；文獻[5]研究并制造出一種柔性平板式二維平臺，通過對微動平臺的靜、動態特性進行了實驗測試，實驗結果表明微動平臺的定位精度達到了納米級，一階模態與二階模態的固有頻率分別為495.7Hz和521.8Hz；文獻[6]用雙圓弧柔性薄板結構，采取拓撲優化設計方法和有限元分析法相結合的方式，研制出二維并聯壓電微動平臺，沿x、y方向能夠實現的位移分別為22.67μm、23.26μm，最大固有頻率約為1.35kHz；文獻[7]應用通過有限元方法建立了微動工作臺靜、動特性分析模型，提出一種納米級x-y-θ微動工作臺的運動構思，并應用正交試驗設計分析了參數對微動工作臺的靜、動特性的影響關系；文獻[8]設計的微動平臺，應用有限元分析結合解析法研制而成，它由兩個不同的平臺組裝，該平臺結構設計上采用柔性薄板結構，該平臺在平面內可實現了微小的平動和轉動；文獻[9]采用圓弧柔性鉸鏈，應用有限元分析法設計出一種3-RRR并聯柔性微動平臺，該平臺可以實現微小的轉動；文獻[10]設計并制造出新型的壓電陶瓷驅動的微傳動、微進給裝置，該裝置微動的調節范圍為（0～3.2）μm，它的分辨率可以達到1nm，并成功的把它應用于超微精密車削加工設備當中。

2 微動平臺結構設計

項目設計的微動平臺由三個壓電陶瓷執行器完成驅動，在x方向一個壓電陶瓷執行器驅動獲得運動，而在y方向采用對稱雙壓電陶瓷執行器驅動獲得運動，除了獲得x、y方向的直線運動外，通過在y方向兩個對稱壓電陶瓷驅動進給位移的差值，獲得z方向的轉動，通過這一設計理念，假想出一種微動平臺，如圖1所示。

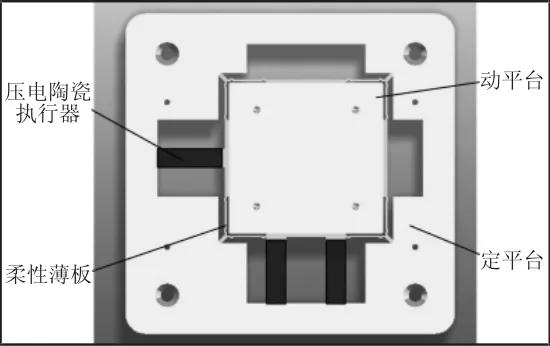
圖1 三維微動平臺的運動原理及結構圖Fig.1 The Movement Principle and Structure Diagram of 3D Micro-Positional Stage

3 理論計算

3.1 微動平臺臺面尺寸確定

該微動平臺的動力力學分析采用牛頓-歐拉方程運動原理進行分析求解，在工作的過程中，微動平臺所受的驅動力的受力分析表達示意，如圖2所示。微動平臺的尺寸為a×b，在以O軸為xoy坐標軸內，微動平臺受力F的驅動，微動平臺在x、y軸方向獲得的加速度分別為 αx和 αy，受到的分力分別為：Fx=Fsinθ，Fy=Fcosθ

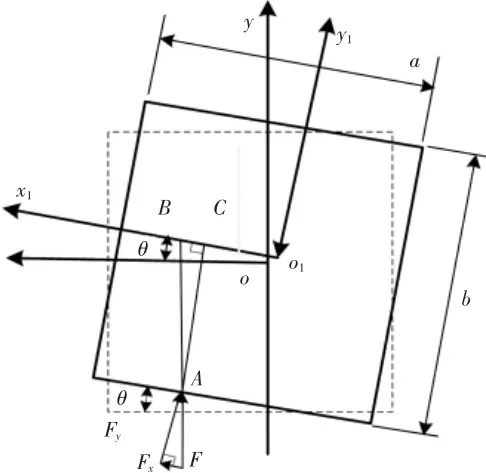
圖2 微動平臺的受力分析圖Fig.2 Force Aanalysis of Micro-Positional Stage

由于本微動平臺的結構為長方體，故微動平臺對其圓心的

式中：MZ—剛體繞z軸轉動的慣性力矩；JZ—剛體在運動過程中

的轉動慣量；α—瞬時角速度。

如圖2所示，根據圖形中描述的尺寸，可知各點的坐標分別為 O（0，0），o1（x，y），力 Fy對微動平臺形心的動量力矩為，根據公式：

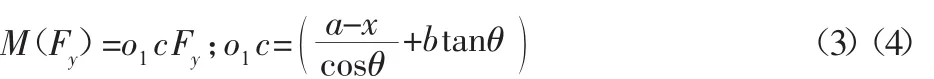
通過計算可得整理后可得，微動平臺的動力學結構方程可

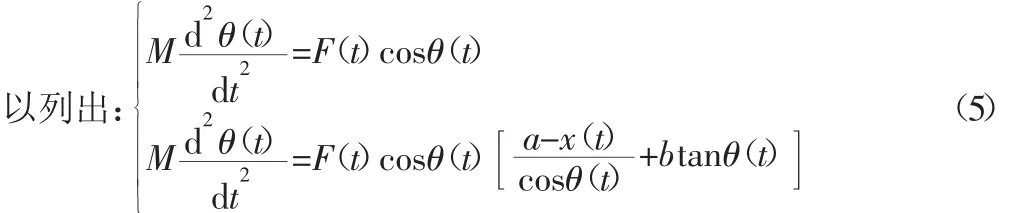
由于微動平臺在整個運動過程中的轉動角度范圍為0°≤θ≤1°，所以可以將公式中的sin θ≈θ，而來進行計算。

3.2 柔性薄板剛度計算

選取半圓形柔性薄板的彎曲剛度作為參數目標，根據半圓形柔性薄板的結構構造，建立力學模型。如圖3（a）所示，圖中：r—內圓弧半徑；R—偏移后外圓弧半徑；h—薄板的高度；b—半圓柔性薄板的厚度。由于在外力矩的作用下，半圓形柔性薄板中間圓弧部分易應生彈性角形變，選擇薄板的尺寸參數的設計和材料的作為驗證指標。由于半圓形柔性薄板在θ角范圍內的薄板高度都為h，故在任意位置截取一段微元a，如圖3（b）所示，微元高度為：a=h=R-r。

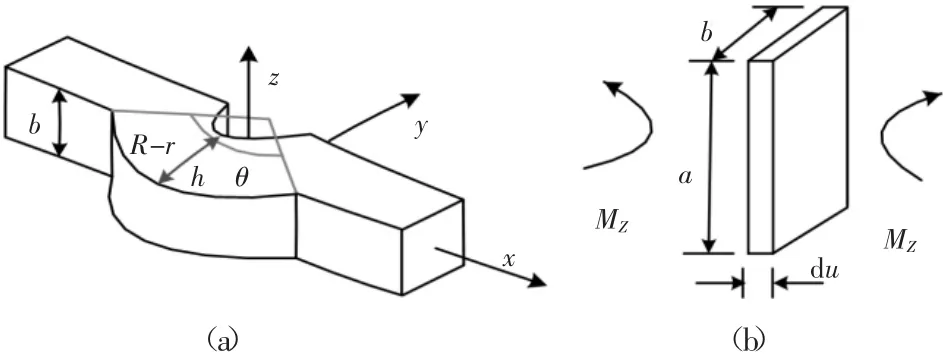
圖3 半圓形柔性薄板和微元尺寸示意圖Fig.3 Half Circular Parallel Structure and Size of Micro-Element’s Chiematic Diagram

由于半圓形柔性薄板為扇形截面，微元的寬度等于R-r，故由扇形面積積分可得

當有力矩MZ作用在微元上時（MZ為由壓電陶瓷執行器驅動力P所引起的轉矩），微元所受力情況，如圖4所示，微元在力矩作用下沿z軸發生的角形變為dαz，由材料力學中的相關的公式，可以列出目標函數：

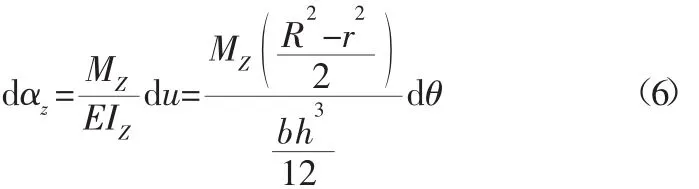
式中：IZ—微動平臺薄板截面的慣性矩；θ—薄板的圓弧角度。

由此，半圓形柔性薄板繞z軸時的轉動剛度方程可以列出：

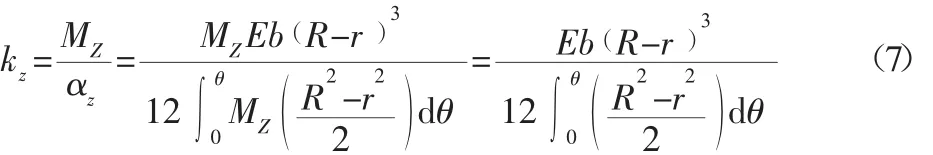
式中：E—微動平臺薄板所采用材料的彈性模量；B—該薄板的寬度。

由于該平臺設計時，x方向和y方向結構相同，為此這兩個方向的參數方面就基本相同。故設計的薄板機構為四個柔性連接薄板臂，共計8個柔性薄板組成，如圖4所示。

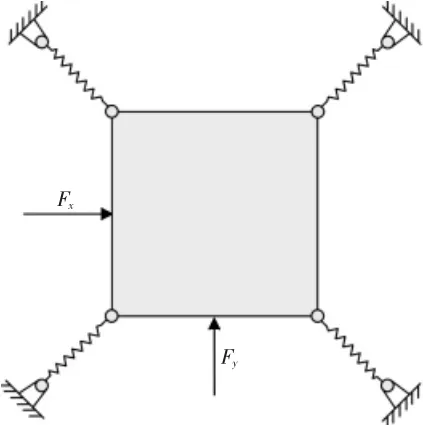
圖4 微動平臺機構簡圖Fig.4 Mechanism of Micro-Positional Stage Diagram

微動平臺的柔性薄板在x和y方向上在施加外力時，柔性薄板所產生的最大應力應小于材料的能夠承受的許用應力，即材料本身的剛度要足夠，材料的轉動剛度公式：K=式中：E—薄板選定材料的彈性模量；I—薄板選定材料的慣性矩；

L—薄板的長度。

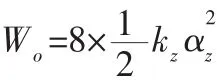
由薄板轉動剛度-圓弧寬度（k-b）曲線圖和薄板轉動剛度-薄板圓弧半徑（k-R）曲線圖中，經過校核實驗，確定尺寸。當微動平臺在彈性恢復力Ft施力下，微動平臺想要實現平面內平動ΔX距離時，平臺在運動過程中所做的功為：W=FtΔX

微動平臺X、Y方向共8個柔性薄板，8個柔性薄板儲存積聚的總彈性勢能為

式中：αz—薄板發生形變時所引起的角變形；kz—薄板的轉動剛度。

由能量守恒定律可得：彈性恢復力Ft，在工作狀態下所作的功W，應該與微動平臺8個柔性薄板儲存的總彈性勢能Wo相等，薄板的彈性恢復力計算公式可以轉換成：

由于αz是柔性薄板形變所引起的角變形，它的角形變數值很小，故可以近似看做αz≈tanαzr

要實現微動平臺Δx=0.04mm的位移輸出距離，通過前面公式（7）可以推算出，該柔性薄板的彈性恢復力為：

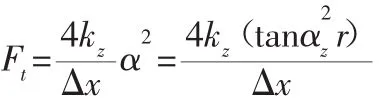
通過帶入數據，可以得出該柔性薄板的彈性恢復力。可以推出，要實現Δx=0.04mm的位移輸出距離，該柔性薄板的剛度可以列出

微動平臺的運動簡圖，如圖5所示。由于該柔性薄板結構的手臂直線方向進給時不會產生附加動作，現已知每個薄板的剛度kt，由受力關系可以表達出，故微動平臺的剛度kp表達式可以列出：

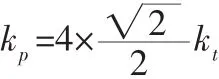
3.3 沿x、y的輸出位移計算

由于微動平臺受到驅動力的過程中，微動平臺的運動相當于一個彈性運動彈簧，由胡克彈性定律描述出，故微動平臺在x、y受到驅動力的作用下，微動平臺發生的位移可以列出：

式中：k—物質的彈性系數，它只由材料的性質所決定，與其他因素無關；F—是材料所受的應力；Δx—驅動力下所產生的應變。

3.4 繞z軸輸出轉角計算

由于微動平臺要實現在z軸方向的轉動，在單獨Fy1、Fy2或兩個Fy1、Fy2的輸入差值驅動力的作用下，使平臺發生了相應的轉動，由于微動平臺在驅動力的作用下所引起的角變形的數值很小，故微動平臺引起的角變形近似等于微動平臺的平動位移Δx，微動平臺產生的轉動角度應等于產生的角形變與微動平臺長度尺寸的比值，故公式（10）可以列出：通過理論計算，加工出三維微動平臺。

4 微動平臺的實驗測試

4.1 微動平臺的位移測試

微動平臺的位移特性測試實驗室系統的組成包括壓電執行驅動電源、計算機、微動平臺、多功能數據采集卡、電渦流位移傳感器和壓電陶瓷驅動器等，如圖5所示。其工作的原理如下：首先由計算機生成需要的驅動電壓波形，輸出的波形輸入到多功能數據卡上的D/A轉化器，再由D/A轉化器控制壓電陶瓷執行器驅動電源，然后驅動電源將施加在壓電陶瓷執行器上，而壓電陶瓷執行器將在驅動電壓的作用下發生形變產生驅動力，驅動力施加在微動平臺后，使得微動平臺發生微小位移輸出，產生的微小位移輸出由電渦流位移傳感器測出其具體的位移輸出值，最后經過多功能數據采集卡上的A/D轉換器將數據采集到計算機內，通過顯示器顯示出參數。在進行微動平臺的位移測試時，在90V驅動電壓作用下，壓電微動平臺進行位移輸出，取平均值后輸出。

圖5 位移特性測試實驗系統Fig.5 Experimental System for Measuring Displacement

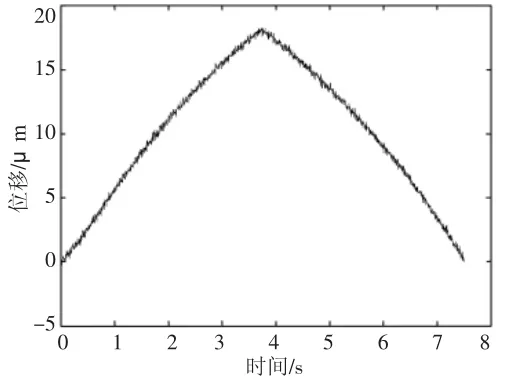
圖6 x方向上的輸出位移Fig.6 Displacement of Mmicro Positional Stage in x Direction

當x方向的壓電陶瓷執行器進行驅動微動平臺時，y方向上的左右兩側壓電陶瓷執行器均預緊狀態下，微動平臺的輸出位移，如圖6所示。x方向的最大輸出位移大約為18.40μm。當y方向左右側壓電陶瓷執行器同時驅動微動平臺時，平臺的輸出位移，如圖7所示。y方向的左右的最大輸出位移分別約為18.65μm和19.04μm。

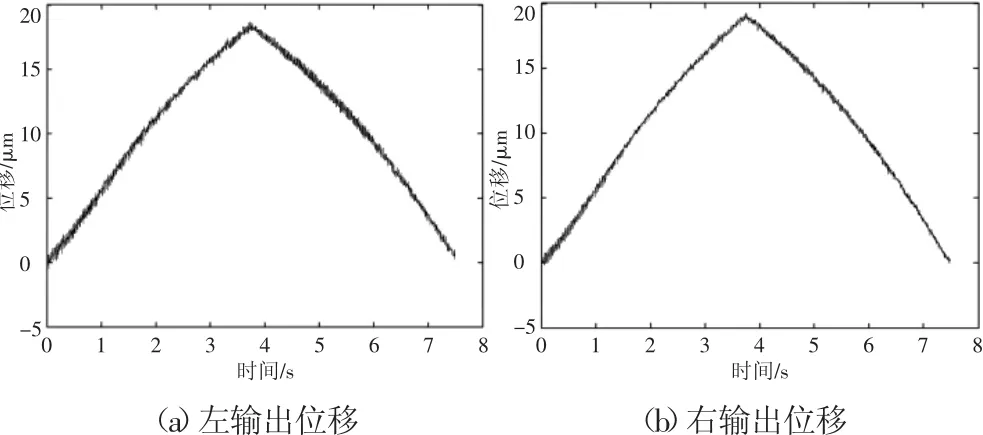
圖7 y方向上的輸出位移Fig.7 The Output Displacement Micro-Positional Stage in y Direction

4.2 微動平臺固有頻率測試

微動平臺進行頻率響應特性測試的實驗系統有由重錘、壓電加速度傳感器、電荷放大器和FFT分析儀構成，如圖8所示。實驗測試的工作原理為：首先用重錘沿平臺運動方向上敲擊微動平臺給平臺施加一個沖擊信號，產生的沖擊信號會被輸入到FFT分析儀中；然后，微動平臺運動部分的響應被壓電加速度傳感器感知，產生的電荷信號被壓電放大器轉換為壓電信號后輸入FFT分析儀中，最后通過FFT分析儀輸出得到微動平臺在各方向上的頻率響應特性參數。通過上述試驗系統，分別對微動平臺x、y及繞z軸轉動的方向進行固有頻率特性測試，測試結果，如圖9所示。三個固有頻率分別x方向固有頻率為2.25kHz，y方向固有頻率為2.28kHz，繞z軸轉動的固有頻率4.01kHz。

圖8 頻率響應特性測試實驗系統Fig.8 Experiment System for Measuring Frequency Response Characteristic

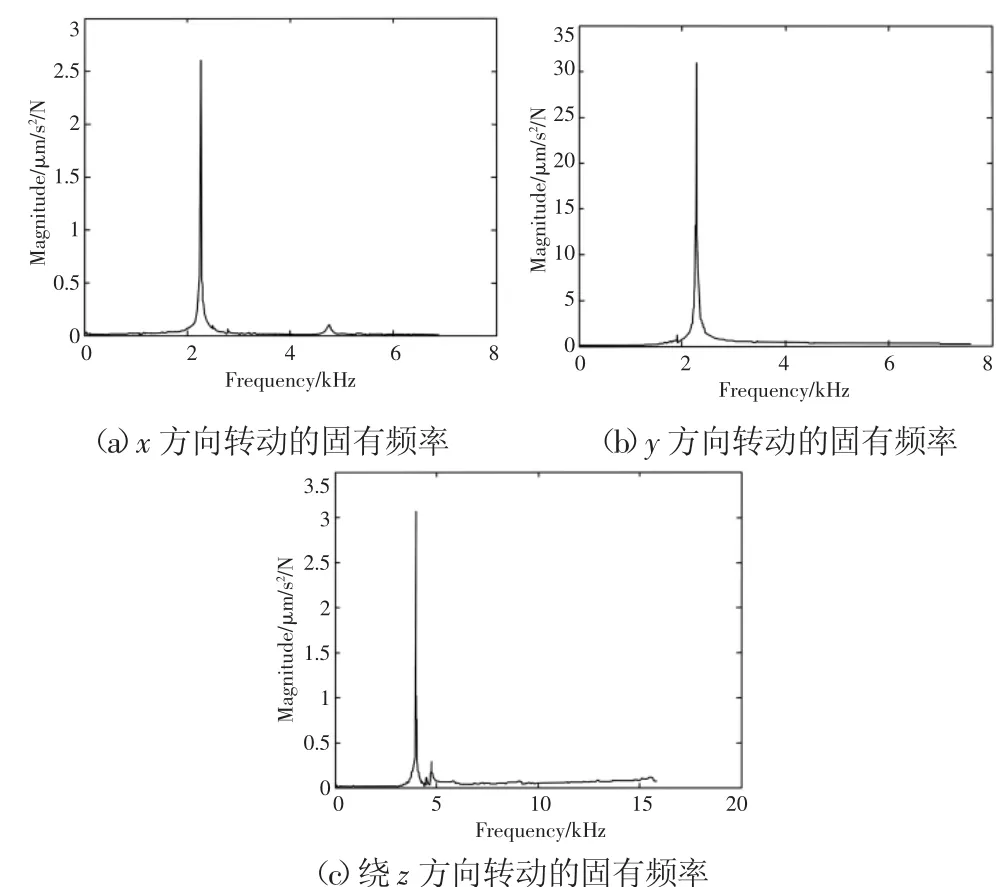
圖9 平臺的頻率響應Fig.9 Frequency Response of Stage

5 結語

通過預期輸出位移目標對微動平臺進行相關的結構設計和理論計算，然后在90V的最高驅動電壓下，對微動平臺進行位移特性曲線測試，結果表明x方向的位移為18.40μm，y方向的左右的位移分別為18.65μm和19.04μm；再次，通過對平臺固有頻率特性曲線測試，結果顯示微動平臺在x、y及繞z軸轉動的方向的固有頻率分別為 2.25kHz，2.28kHz，4.01kHz。

［1］李慶祥，王東生，李玉和.現代精密儀器設計［M］.北京：清華大學出版社，2004.（Li Qing-xiang，Wang Dong-sheng，Li Yu-he.Modern Precision Instrument Design［M］.Beijing：Tsinghua University Press，2004.）

［2］段瑞玲，李玉和，李慶祥.一種用于微器件裝配的系統設計與研制［J］.新技術新工藝，2006（5）：30-33.（Duan Rui-ling，Li Yu-he，Li Qing-xiang.A system design and development for micro device assembly［J］.New Technology and New Process，2006（5）：30-33.）

［3］姚楠，王中林.納米技術中的顯微學手冊［M］.北京：清華大學出版社，2006.（Yao Nan，Wang Zhong-lin.Handbook of Nano-Technology in Microscopy［M］.Beijing：Tsinghua University Press，2006.）

［4］吳鷹飛，周兆英.柔性薄板的設計與分析［J］.機械設計與研究.北京.2006.（Wu Ying-fei，Zhou Zhao-ying.Design and analysis of flexible sheet［J］.Machinery Design and Research，2002，24（2）：41-46.）

［5］榮偉彬，馬立，孫立寧.二維微動工作臺分析及其優化設計方法［J］.機械工程學報，2006，42（5）：26-30.（Rong Wei-bin，Ma Li，Sun Li-ning.Analysis and optimum design of 2-DOF micro-positioning stage［J］.Chinese Journal of Mechanical Engineering，2006，42（5）：26-30.）

［6］淳華.基于拓撲優化方法的二維柔性結構微動平臺研究［D］.寧波：寧波大學，2010.（Chun Hua.Topology optimization method based on the 2D flexible structure of micro-positioning stage research［D］.Ningbo：Ningbo University，2010.）

［7］朱仁勝，沈健，趙韓.精密微動平臺［J］.航空制造技術，2008（10）：82-86.（Zhu Ren-sheng，Shen Jian，Zhao Han.Precision micro-positioning stage［J］.Aeronautical Manufacturing Technology，2008（10）：82-86.）

［8］Yong-Fong Fung，Wang-Chi Lin.System identification of a novel 6-DOF precision positioning table［J］.Sensors and Actuators A，2009（150）：286-295.

［9］JAE W.RYU，SUNG-Q LEE DAE-GAB GWEON，KEE S.MOON.Inverse kinematic modeling of a coupled flexure hinge mechanism［J］.Mechatronics，1999（9）：657-674.

［10］Yong Li，Min Guo，Zhaoying-Zhou.Micro electro discharge machine with an inchworm type of micro feed mechanism［J］.Precision Engineering，2001，8（3）：261-264.