淺析小學數學估算教學的策略
姚漢明

【摘要】本文論述在小學數學教學中科學地掌握估算策略,靈活地運用估算策略,有利于提高學生分析問題、解決問題的能力,提升學生思維的深刻性、靈活性和獨創性。
【關鍵詞】估算教學 計劃性 合理性 準確性 規律性 整體性
【中圖分類號】G 【文獻標識碼】A
【文章編號】0450-9889(2018)09A-0127-02
估算在日常生活與數學學習中有著十分廣泛的應用,在數學教材的許多領域也留下估算的足跡。所謂估算策略是指運用估算幫助學生解決實際問題的一種途徑和方法,它具有較強的針對性和靈活性。學生掌握基本的估算方法并不難,但是靈活運用估算策略卻不容易。在不同的情境下,估算的策略是不同的,所以教師要引導學生根據實際問題靈活選擇不同的估算策略,提高學生的分析、判斷能力,促進學生思維深刻性、靈活性和獨創性的進一步發展。
一、計劃性估算
在日常生活中,人們在處理某種事情時,往往需要事先根據事情的實際情況做出粗略的估計,做到“心中有數”。比如買菜時事先估算一下要帶的費用、外出游覽時估算一下花費、根據上班途中所需時間來確定出發的時間、造房裝修費用、鋪地面需要多少塊地磚等都要進行預估,只有這樣,才能有計劃地處理事情。在數學學習過程中對要解決的問題提前進行計劃性估算,能夠進一步提高解決問題的效率。如在學習了小數的加減法后,筆者創設了這樣一個情境:一個文具盒8.95元,一支自動筆4.10元,一本筆記本2.85元,一把圓規4.75元,一本練習本1.50元,一支鋼筆15.20元等,小明要買其中兩種不同的學習用品,最多要付給營業員多少張5元的鈔票?最少呢?運用估算就能快速準確地付錢了。又如學校禮堂里有28排坐椅,每排有32個座位,學校禮堂大約能坐多少人?學生通過把28、32分別估算成30和30,很快就能估算出學校禮堂大約能坐的人數。這樣的情境創設不僅讓學生體會到估算對解決問題的便捷、準確,而且讓學生理解了求精確數與近似數的區別。
二、合理性估算
所謂合理性估算,就是借助已有的生活經驗和知識經驗,對要解決的問題運用估算,使其符合生活實際,具有合理性。如學生在使用計量單位時常常會出現這樣的錯誤:一桶純凈水18毫升、小蘭身高13厘米、一個金魚缸的體積是200立方米……這樣的答案在學生的作業中屢見不鮮。教師要運用估算的策略使學生明白這樣的結果是脫離生活實際的,是不合理的:一桶純凈水比1升要多得多,而18毫升只是一點點;13厘米和我們平時用的直尺差不多長,有這么矮的人嗎?200立方米就是200個棱長是1米的正方體,那是多大的空間啊……這些都是生活常識,學生有一定的生活經驗,當老師把這些問題擺到他們的面前時,他們就會哄堂大笑,但是在寫作業的時候卻想不到。所以,在教學中教師要引導學生聯系生活實際,找準合理的參照標準,進行有效估計,促使問題的答案更具合理性,進而避免類似錯誤發生。
三、準確性估算
計算出錯是學生作業中普遍存在的問題,很多人認為是粗心大意造成的,但筆者認為,這些問題很大程度上是學生對計算的結果缺乏正確的思考和估計。如果學生在計算前進行估算,就能為計算的準確性做好鋪墊,大大提高計算的準確率;計算后進行估算,就能很快判斷出計算結果有沒有錯誤,以便找到錯誤原因,及時糾正。例如教材練習中設計了大量的“先估一估得數是幾十多”“先估一估積是幾位數”“先估一估商是幾位數”和“先估一估商的最高位是幾再計算”等(圖1),這種問題的設計,就是要求學生計算前要養成估算的習慣;計算68×72=□,讓學生通過估算弄清正確的結果應在4200到5600之間;學校五子棋興趣組男生平均身高138厘米,女生平均身高134厘米,興趣組同學的平均身高必須在134厘米至138厘米之間。又如,檢驗201+232-365=□,先看計算結果的尾數是不是8;計算59×64=□,先看計算結果的尾數是不是6;檢查468÷26=18的結果是否正確時,也只要看除數和商的尾數相乘的積的尾數與被除數的尾數是否一致……如果學生有了這樣的意識,掌握了這樣的估算方法,計算錯誤就會大大減少。
四、規律性估算
所謂規律性估算就是運用數學計算中的規律進行的估算。教材設計了很多規律性的練習,引導學生根據其中蘊藏的規律進行估算,就能很快找到正確的答案。如教材中設計了“不計算,在○里填上>、<或=”的練習(圖2),以乘除法為例:0.89×1.25○0.89,0.89×1.25○1.25,0.89÷1.25○0.89,0.89÷1.25○1.25……解答乘法計算時可以引導學生根據“一個因數(0除外)乘以小于1的數,積就小于這個因數;一個因數乘以大于1的數,積就大于這個因數”這樣的規律進行估算;解答除法計算時可根據“除數大于1,商就小于被除數;除數小于1,商就大于被除數”的規律進行估算,這樣就能很快確定○里填什么符號。
五、整體性估算
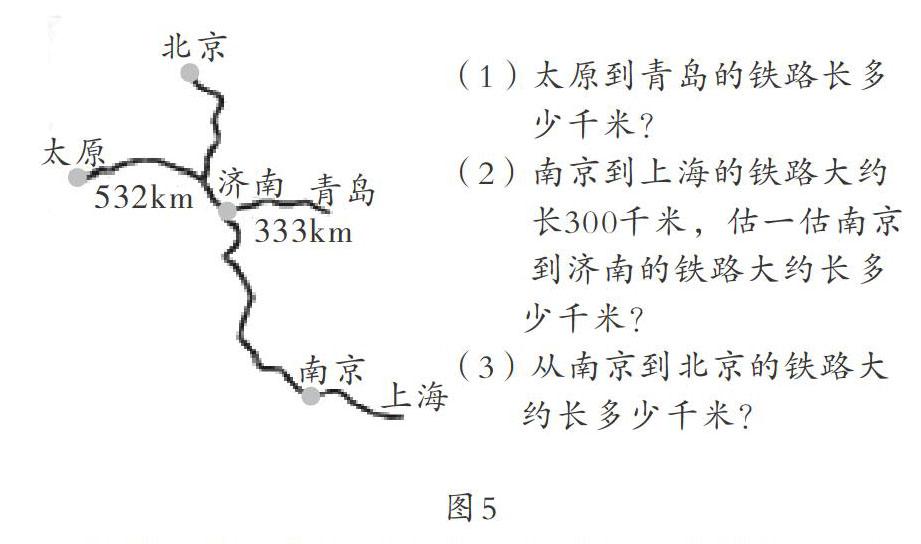
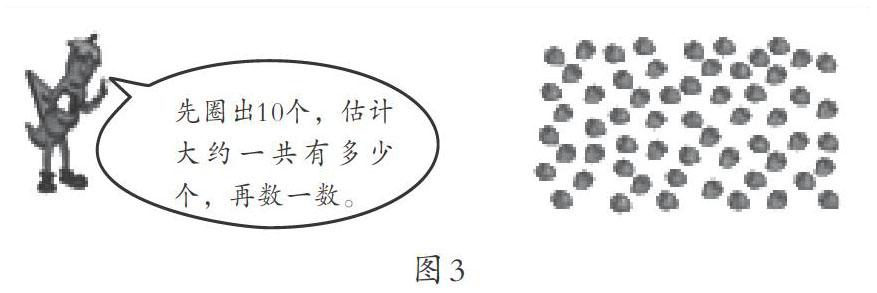
所謂整體性估算就是把一個整體分成若干等份,根據部分數估算出整體數。例如,蘇教版數學一年級上冊《100以內數的認識》,就有這樣的練習(圖3):先圈出10個,估計大約一共有多少個,再數一數。教學時筆者引導學生先圈出10個草莓,再啟發學生思考這堆草莓有幾個這樣的10個,大約就是幾十個。又如三年級學習了認識分數后安排了這樣的估算練習(圖4):《科學天地》大約占黑板報板面的幾分之一?《藝術園地》大約占黑板報板面的幾分之一?教學時筆者引導學生把黑板報版面看作一個整體,《科學天地》占整個版面的二分之一,《藝術園地》版面就占整個版面的四分之一。再如,學習《認識千米》后,設計了這樣的估算練習(圖5):南京到上海的鐵路大約長300千米,估一估南京到濟南的鐵路大約長多少千米?南京到北京的鐵路大約長多少千米?這里要求學生借助南京到上海的路程去度量南京到濟南、南京到北京的路程中有幾個南京到上海的路程,它就有幾個300千米。
估算策略的掌握是學生估算能力的具體體現,由于每名學生都是一個獨立的個體,存在一定的差異性,他們對數學知識的理解、數學技能的掌握都不一樣,在估算時不同的學生必然會產生不同的估算方法。因此,教師必須尊重每一名學生,讓學生充分表達自己的想法,解釋估算的過程,體驗不同的解決問題的方法,從而提高學生的估算能力。當然,估算能力的養成是一個長期的過程,教師在日常教學中要把估算和精確計算結合起來,努力創設和捕捉一切可利用估算教學的課程資源,為學生創造一些估算的機會,讓學生在估算活動中體驗成功的喜悅,進而將估算內化為一種自覺行為,養成估算的習慣,并將這個習慣運用到數學學習中。

