基于LES-FE-SEA混合方法的車內湍流噪聲數值預測與控制研究?

宗軼琦，谷正氣，2，張 勇，江財茂，張啟東，楊振東

1.湖南大學，汽車車身先進設計制造國家重點實驗室，長沙 410082；2.湖南文理學院，常德 415000；3.湖南工業大學機械工程學院，株洲 412007；4.廣州汽車集團股份有限公司汽車工程研究院，廣州 516434

前言

汽車在高速行駛過程中，車內氣動噪聲可視為乘員室聲腔對車外氣流脈動壓力作用的氣動聲學響應[1]。隨著生產商與消費者對汽車的乘坐舒適性要求不斷提高，如果產品的氣動噪聲與產品的檔次不相稱，就會影響汽車品牌的總體印象與評價。因此，準確計算與降低汽車乘員室聲腔的氣動噪聲水平具有重要的現實意義。

目前，國內外學者對車內乘員室噪聲進行了廣泛研究。其中，文獻[2]中采用混合FE-SEA方法預測了某乘用車車身前圍板聲學傳遞損失，并與測試結果進行綜合比較，從而在全頻段范圍內，確定了結構優化區域。文獻[3]中在解決聲腔聲固耦合問題時，考慮了區間參數不確定因素，從而提高了混合FE-SEA方法的計算精度。文獻[4]中對某轎車車型建立了混合FE-SEA模型，通過試驗對動力總成懸置激勵和車身懸置激勵進行了測量，對車內噪聲進行了預測。文獻[5]中建立了車身側圍空腔阻隔結構的隔聲性能預測模型，混合模型預測性能與試驗結果對比表明，混合FE-SEA模型在中高頻能有效預測阻隔結構隔聲性能，而這些研究主要基于結構—聲的計算探討，還沒有與湍流邊界層脈動壓力引起的氣動噪聲研究聯系起來。文獻[6]中對列車地板鋁型材建立了混合FE-SEA模型，并采用聲橋技術、增加材料厚度等方式，顯著降低了輻射噪聲水平。文獻[7]中采用FE-BEM-SEA預測模型對發動機齒輪室蓋結構噪聲進行了深入研究，并采用均勻拓撲優化方法對其進行聲學包裝，獲得了較為理想的降噪效果。文獻[8]中依據某車型的統計能量分析模型與混合模型，采用鋼化夾層玻璃與PMMA兩種材料優化方案，達到了良好的降噪效果。綜上所述，采用混合LES-FE-SEA方法，在汽車設計階段準確預測具有高強度、全頻段特性的氣動噪聲水平，并基于混合模型對車身子結構進行合理的聲學優化或采取相應的降噪措施，對提升汽車自身品牌競爭力具有重大意義。

本文中基于上述現狀，以某轎車為研究對象，應用CFD軟件與混合FE-SEA技術，建立了車身流固耦合模型。通過計算分析混合模型各子系統對乘員室的噪聲貢獻量，確定對車內噪聲影響較為顯著的結構部件。最后采取非支配排序遺傳算法對乘員室聲腔結構進行多目標優化，確定了使降噪幅度和效率等指標達到最為合理時的各層吸聲材料厚度的最佳布置方案。

1 混合LES-FE-SEA方法實現

1.1 湍流模型采

用大渦模擬(LES)對氣動噪聲進行湍流環節的計算，該方法能比傳統的雷諾應力平均RANS湍流模型取得更好的模擬效果。LES方程是通過對N.S.方程進行波數或物理空間過濾而得到的一個大尺度運動方程，其形式[9]為

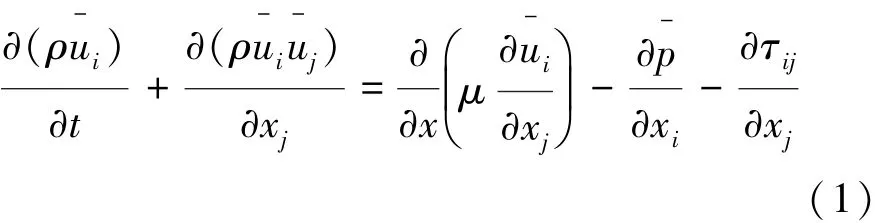
式中： ρ為流體密度； ui，uj為速度分量； xi，xj為方向坐標；t為時間；μ為黏性系數；τij為亞格子尺度應力，體現了小尺度漩渦運動；p為壓強。

為使方程封閉，采用渦旋黏性亞格子模型(SGS)，其形式為

式中：右端第2項是一個對角張量，常被并入壓強項中計算，因此在建立亞格子模型時通常不予考慮；μt-為渦黏系數；Sij為濾波后得到的可解尺度場的應變張量分量。

1.2 FE-SEA混合系統方程

在采用混合模型進行數值仿真之前，須確定模型的輸入激勵，因此將CFD計算獲得的表面脈動壓力值轉化為各結構子系統的平均壓力譜，并將其作為力載荷施加至混合模型。

當系統的確定性邊界位移為零時，混響場所產生的力載荷滿足以下統計學關系[10]：

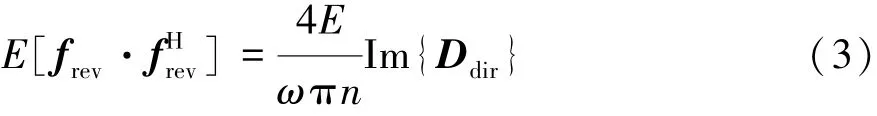
式中：E[…]為均值；E為子系統的統計能量響應；frev為子系統確定性邊界處的混響場力載荷，可與其能量響應建立起一種統計性聯系[11]；H表示共軛；n為模態密度；ω為圓頻率；Im表示虛部；Ddir為子系統的確定性邊界處的動剛度矩陣。

當車身板件的位移為q時，直接場在邊界處產生的作用力為Ddirq，同時考慮到邊界處的混響場載荷frev，邊界處總的邊界力為

FE-SEA混合模型中FE子系統與SEA子系統可以通過式(3)耦合，因此FE子系統的運動方程為

式中：Dd為連接邊界處子系統的動剛度矩陣；D(k)dir為第k個子系統的直接場動剛度矩陣；Sqq為子系統的位移互譜矩陣；Sff為子系統激勵力互譜矩陣；Ek為第k個子系統的振動能量；nk為第k個子系統的模態密度。

因為各個子系統之間的功率流動保持平衡，FESEA混合方法的耦合功率平衡方程[13]為

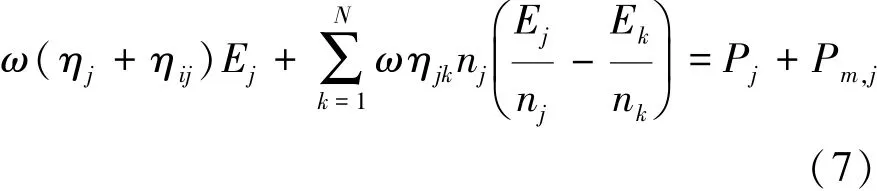
式中：ηj為第j個子系統的內損耗因子；ηij為第i個子系統與第j個子系統的耦合損耗因子；Pj為第j個子系統的輸入功率；Pm，j為確定性系統上的力所產生的輸入功率。

通過式(6)和式(1)可分別得到確定性子系統的響應和系統的能量響應。

2 混合模型仿真計算與驗證

2.1 建立混合模型

本文中以某轎車為研究對象，根據子系統帶寬Δf內的振型數可對頻率范圍進行劃分[14]：當N≤1時，定義為低頻區；當1＜N＜5時，為中頻區；當N≥5時，為高頻區。依據模態相似原則劃分車身表面結構子系統，以保證SEA子系統擁有滿足統計能量分析需求的較高模態密度(分析帶寬內的模態數不低于5)，同時FE子系統在分析帶寬內的模態數不高于5。根據以上原則，整車FE-SEA混合模型共劃分為162個子系統，其中SEA平板子系統106個，SEA曲面板子系統14個，SEA聲腔系統6個，FE子系統36個。各子系統通過點線面耦合連接，形成一個整體，最終實現各個相應結構之間的能量正常流動，其中乘員室聲腔模型和FE-SEA車身表面連接模型分別如圖1和圖2所示。

圖1 乘員室聲腔模型

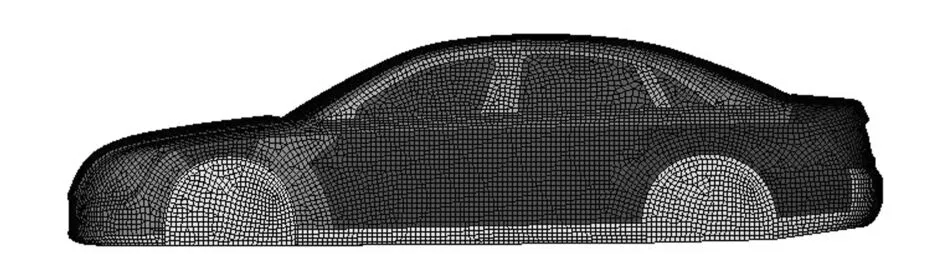
圖2 FE-SEA車身表面連接模型

依據混合FE-SEA方法對聲源輸入信號的條件要求，將車身表面結構子系統的脈動壓力轉化為平穩均勻的聲壓頻譜，并將其作為計算模型的激勵輸入。在進行流體動力學計算前，先對流體計算域劃分網格，車身周圍網格分布如圖3所示，為保證后續環節擁有較高的計算精度，在流體動力學穩態計算結束后，以車身表面的等靜壓云圖(見圖4)的疏密分布情況為參考，在各子系統表面選取若干個監測點：在靜壓較強的區域，適當增加監測點數量；在靜壓較弱和變化較為緩和的區域可適當減少監測點數量，左前側窗監測點如圖5所示。在進行風速為30m/s時的瞬態LES計算時[15-16]，啟用FW-H聲方程，計算得到各監測點的脈動壓力譜，然后通過FFT變換和對數轉換，最終獲得左前側窗系統平均偶極子聲壓譜，如圖6所示，同時可獲得前風窗、后側窗和門板等結構子系統的平均聲壓譜，并將其作為激勵施加至FE-SEA模型，其中FE子系統上載荷施加方式如圖7所示。

圖3 CFD計算中車身周圍網格分布

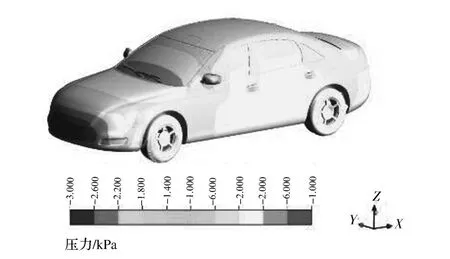
圖4 車身表面靜壓云圖

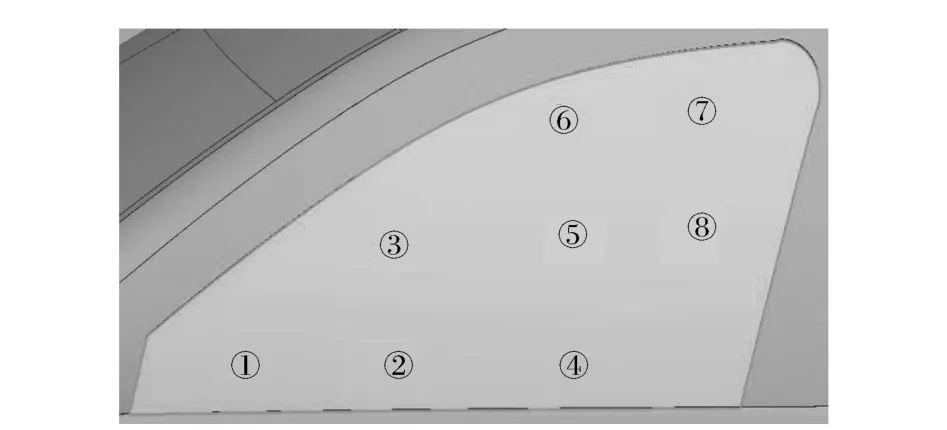
圖5 左前側窗監測點位置

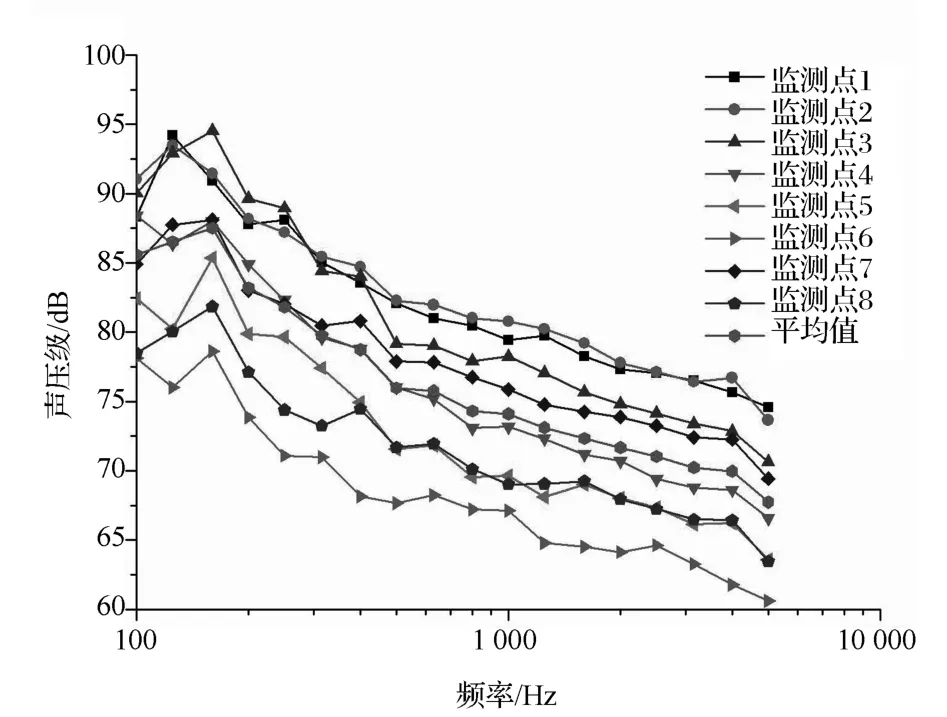
圖6 監測點平均聲壓譜

圖7 FE子系統載荷施加方式

2.2 實車道路試驗與結果分析

依據車內噪聲道路測試標準規定，測量跑道選擇具有足夠長度的清潔、干燥、較為光滑、平坦(縱向坡度在0.1%以內)的某瀝青高速公路。氣象條件要求為無雨、無霧、風速不大于5.6m/s的晴朗天氣，為將外界干擾降到最低，選擇試驗時間段為某日凌晨3-4點，同時，為減少發動機噪聲對試驗結果的影響，在汽車加速至108km/h時，將汽車發動機關閉，脫擋滑行，利用LMSTest.Lab噪聲測試儀器采集試驗數據。此過程重復3次，取平均值，傳聲器的布置嚴格依據GB/T 25982—2010，如圖8所示。

圖8 實車道路試驗儀器布置

為了驗證混合方法的可靠性與準確性，采取傳統FE和SEA計算方法與其進行比較，結果如圖9所示。由圖可見：在20～200Hz低頻區，FE模型計算結果與試驗結果較好吻合，能準確捕捉到響應峰值；SEA模型在20～200Hz低頻區與試驗結果對比誤差較大，最大達10dB，精度較差，但是在500Hz以后的高頻區能與試驗結果較好吻合；FE-SEA模型在20～100Hz低頻區能捕捉到響應峰值，但與試驗結果有些差距，計算精度也低于FE模型，從100Hz開始其計算精度逐漸提高，特別是在200～500Hz的中頻區域，FE-SEA模型計算精度比其它兩種方法都高；在滿足各結構模態數的理論假設條件下，500Hz以后的高頻區計算結果與試驗結果較為一致。

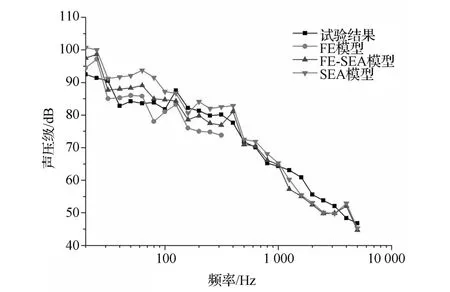
圖9 駕駛員耳旁聲壓級頻譜曲線對比

汽車車身表面各部件的偶極子分布情況對乘員室內部聲腔的噪聲貢獻有直接影響，如圖10和圖11所示，其中后視鏡區域1與2處曲率較大，引起氣流分離，導致壓力脈動變化劇烈，因此聲功率級較高。在氣動噪聲計算與控制過程中，通常關注的是乘員耳旁的噪聲水平，因此以駕駛員與副駕駛耳旁的聲功率輸入大小作為噪聲貢獻量的評價指標，結果如圖12所示。經分析可發現，由于風窗玻璃的剛度較低，隔聲效果較差，前風窗和左右側窗是最大的聲功率輸入子系統，頂棚和左右側圍次之，而儀表板在中高頻區域對輸入功率也有明顯的影響。因此在進行乘員室聲學優化時，須在左右側窗、前風窗、頂棚和左右側圍安放吸聲材料。在實際工程應用中，在側窗和前風窗上安放吸聲材料較為困難，因此，僅在左右側圍和頂棚安放吸聲材料。

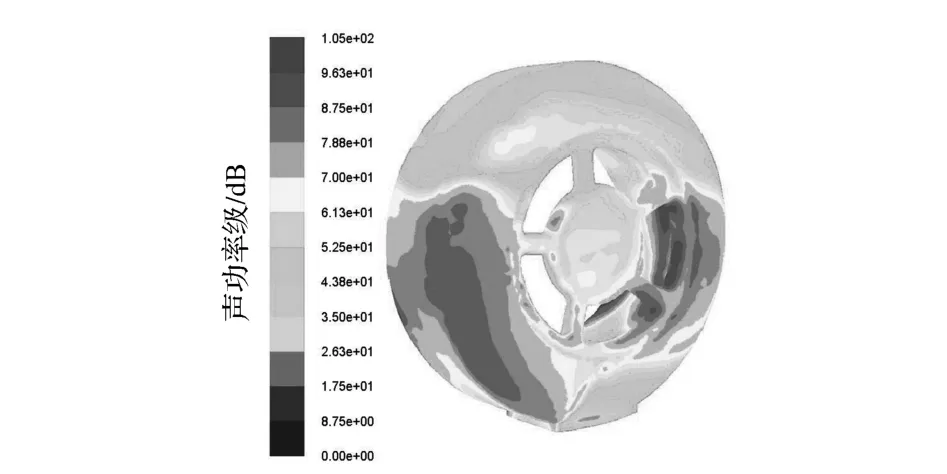
圖10 車輪聲功率級云圖

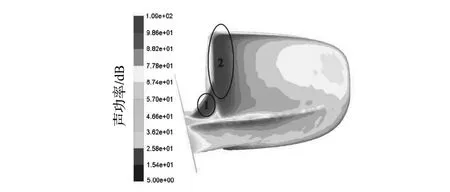
圖11 后視鏡表面聲功率級云圖

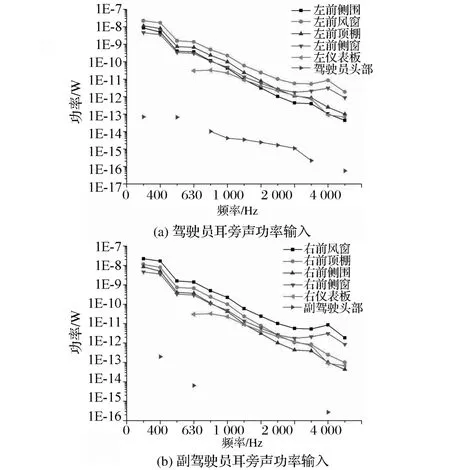
圖12 板件聲功率輸入貢獻量對比

3 乘員室聲學優化

在整車開發過程的仿真中，通常對車輛進行聲學簡化處理，并根據用戶對該樣車總體噪聲水平的期望目標，設計聲學包配置方案，其中乘員室聲腔主要結構板件的吸聲系數的測試現場和測試結果分別如圖13和圖14所示。

圖13 吸聲系數測試

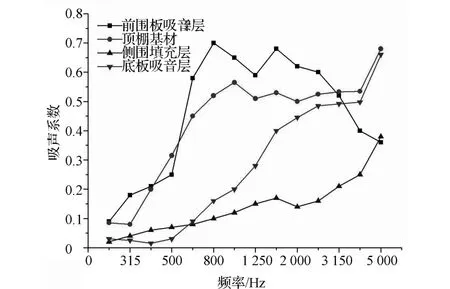
圖14 聲學包主要板件吸聲系數曲線

3.1 確定多目標優化參數

在確定乘員室聲腔主要聲學包參數的基礎上，選取汽車工業中較為常見的4種內飾吸聲材料：工業毛氈、泡沫、鑄造泡沫和玻璃纖維，材料參數如表1所示。將4種材料安放于頂棚和左右側圍，疊放方式如圖15所示。

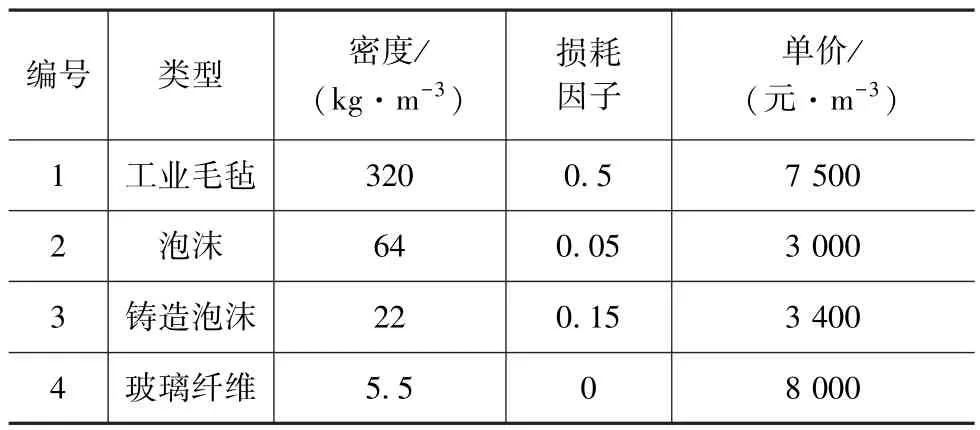
表1 吸聲材料主要參數

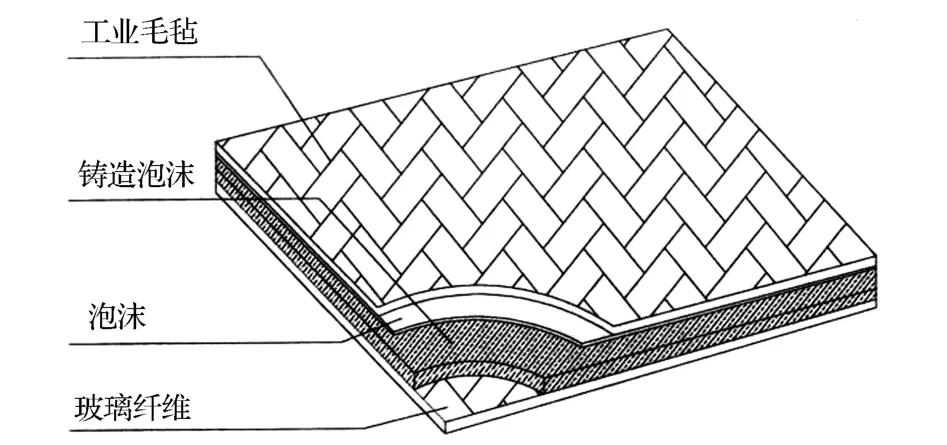
圖15 4層材料疊放方式

選取各層材料厚度為設計變量，分別為工業毛氈厚度d1、泡沬厚度d2、鑄造泡沬厚度d3和玻璃纖維厚度d4。 各設計參數的取值范圍為：d1∈[1.0，3.5]，d2∈[1.0，2.2]，d3∈[2.0，4.0]，d4∈[0.3，6.0]。且為確保乘員室聲腔的空間內外尺寸不受較大程度的影響，要求各層材料厚度之和為10mm。

綜合考慮乘員舒適性、生產成本和車身結構輕量化趨勢，選取降噪幅度S、降噪效率E(降噪幅度與增重之比)、材料成本P和材料性價比K為優化目標，因此該優化問題可描述為

根據汽車生產商和消費者對優化目標要求的側重程度有所不同，S，E，P和K的權重系數分別取0.2，0.3，0.1和 0.2。因為設定了總材料厚度為10mm，所以在下文相關列表中僅列出了d1，d2和d3的有關數據。

3.2 試驗設計

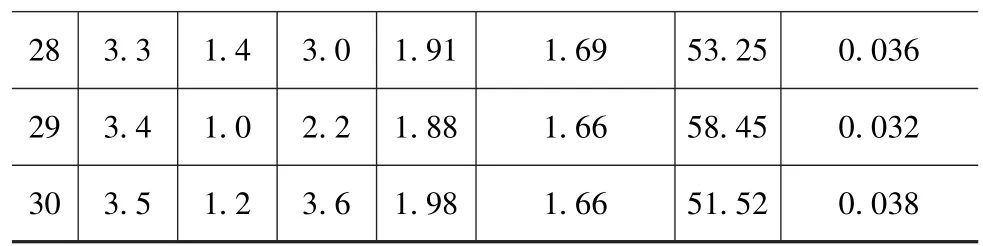
試驗設計是一種對試驗或仿真數據進行有效的數理統計分析的方法，通過制定適當的試驗方案對多目標參數優化問題進行合理的流程設計，獲得理想的優化結果與科學結論[17]。試驗設計方法有很多，其中優化拉丁方法能保證樣本點勻稱地分布在整個設計空間，同時考慮了樣本點間的正交性，因此采用該方法構建30組樣本點，其相應的響應值通過重復性數值計算獲得，如表2所示。

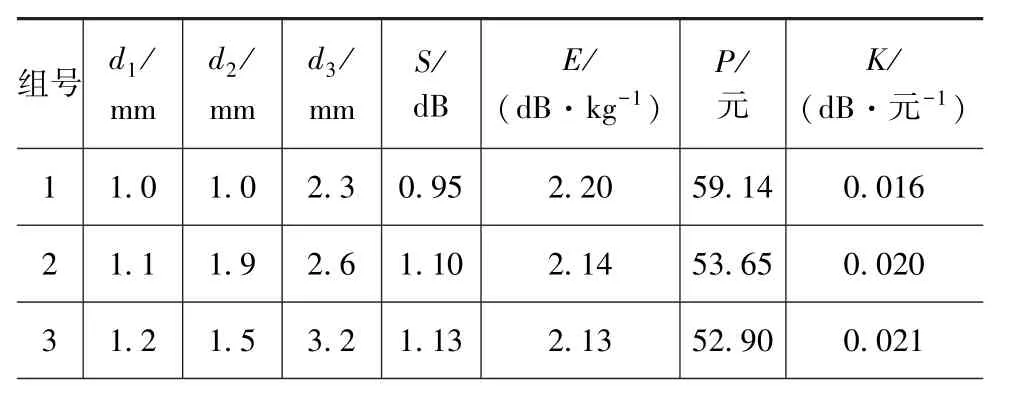
表2 樣本點響應值計算結果

......

3.3 建立近似代理模型

近似代理模型是指在保證計算精度前提下，利用回歸、擬合、插值等方法構造一個運算量小、計算效率高，但計算結果與仿真分析高度相近的數學模型。創建近似模型有多種方法，由于Kriging方法可覆蓋全部樣本點，且獲得的近似面質量較高，故選用Kriging方法創建近似面[18]。

基于表2中優化目標與設計變量之間的響應性關系，選取設計空間范圍中除設計方案以外的任意3組樣本點，進行FE-SEA計算，最后將得出的計算結果同近似模型的結果進行對比，以此來驗證近似模型的精度，如表3所示。

由表可見，在不同的設計變量組合下，通過Kriging方法建立的近似模型計算結果與仿真計算結果之間的相對誤差都在3%以內，表明創建的近似模型能精確地反映響應結果與設計參數之間的關系，因此用其取代原優化目標進行全局優化是穩妥可靠的。

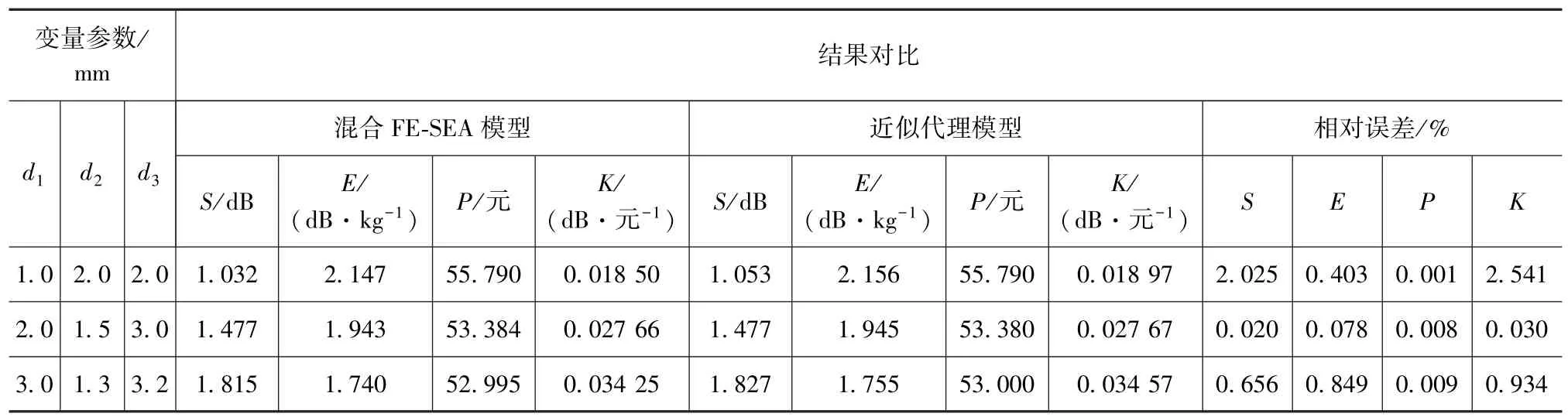
表3 Kriging近似模型的驗證

3.4 分析優化結果

遺傳算法是借鑒達爾文進化論的進化規律演化而來的一種全局搜索優化算法，可同時使用多個搜索點的信息，目前廣泛應用于工程優化領域。非支配排序遺傳算法(NSGA-Ⅱ)是帶精英策略的一種遺傳算法，應用最為廣泛，這種算法通過選擇算子執行之前的非支配排序，避免了傳統算法對權系數的依賴性，同時計算效率高且算法穩定性好[19]。

根據建立的近似模型，采用NSGA-Ⅱ算法進行尋優，最終得到近似模型最優樣本點組合(d1，d2，d3，d4)為(3.1，2.2，4.0，0.7)，對最優材料組合下的優化指標進行混合FE-SEA仿真，其結果與采用近似模型獲得的結果之間的誤差在1%之內，如表4所示。

表4 最佳材料組合下的優化目標誤差對比

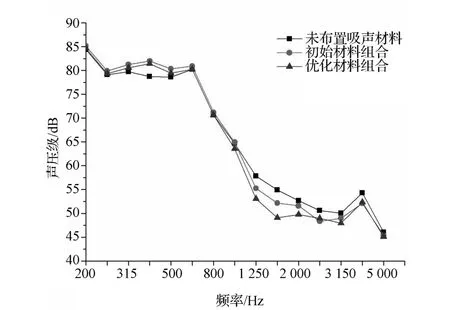
圖16 組合吸聲材料降噪效果對比

駕駛員耳旁聲壓級頻譜曲線對比如圖16所示。由圖可見，在200～500Hz頻段，初始材料組合與優化后的材料組合聲壓級都超出了未安放吸聲材料時的聲壓級，但優化后的材料組合的聲壓級小于初始材料組合的聲壓級；在500～1 000Hz頻段，3種情況的聲壓級差別不大；1 000Hz以后，優化前后的材料組合的聲壓級均比未安放吸聲材料有較大幅度的降低，優化后的材料組合的降噪效果更為明顯。

各優化目標所取權重會影響優化結果。在第3.1節所取得權重條件下，優化效果如表5所示。與初始材料組合相比，優化后的材料組合降噪幅度提高3.15%，降噪效率提升5.05%，材料成本降低23.42%，而性價比提高34.69%。

表5 優化效果

4 結論

(1)采用LES-FE-SEA混合計算模型對車內湍流邊界層脈動壓力引起的氣動噪聲進行預測。混合模型計算結果與實車道路試驗和傳統的FE，SEA方法得到的結果吻合良好，尤其在200～500Hz中頻段時，計算精度更高。為汽車設計階段，氣動噪聲全頻段的高精度預測提供了實際應用模型。

(2)通過混合模型各子系統對乘員室聲學貢獻量的分析，確定適宜貼附吸聲材料的部位為左右側圍與頂棚。利用優化拉丁超立方試驗設計，建立了能高精度、高效地反映優化目標與各層材料厚度參數之間關系的Kriging近似模型。

(3)采用NSGA-Ⅱ優化算法，確定了各層吸聲材料厚度的理想組合。有效地提升了各優化目標，從而改善了乘員室聲學環境，為吸聲材料在汽車風噪控制領域中的應用提供了工程指導。

[1] 楊博，胡興軍，張英朝.汽車后視鏡區域非定常流場與氣動噪聲研究[J].機械工程學報，2010，46(22)：151-155.

[2] SHORTER P，ZHANG Q，PARRETT A.Using the hybrid FESEA method to predict and diagnose component transmission loss[C].SAE Paper 2007-01-2172.

[3] YIN H，YU D，LU H，etal.Hybrid finite element/statisticalenergymethod for mid-frequency analysis of structure-acoustic systems with interval parameters[J].Journal of Sound and Vibration，2015， 353： 181-204.

[4] 陳書明，王登峰，宋學偉，等.基于FE-SEA混合方法的聲腔內部噪聲預測[J].振動與沖擊，2010，29(10)：236-238.

[5] 牛勝福，張立軍，孟德建，等.車身側圍空腔阻隔結構隔聲性能的建模與驗證[J].汽車工程，2016，38(7)：883-888.

[6] LIN L Z， DING Z， ZENG J， et al.Research on the transmission loss of the floor aluminum profile for the high-speed train based on FE-SEA hybridmethod[J].Journal of Vibroengineering， 2016， 18(3)：1968-1981.

[7] 盧兆剛.基于混合FE-SEA方法的汽車薄壁件中頻聲學特性預測及優化研究[D].杭州：浙江大學，2011.

[8] 耿小華.基于FE-SEA和SEA方法的車內中高頻噪聲研究[D].長春：吉林大學，2012.

[9] 朱暉，楊志剛.類車體外流場非穩態特性數值研究[J].空氣動力學報，2012，30(6)：782-785.

[10] CICIRELLO A，LANGLEY R S.Efficient parametric uncertainty analysis within the hybrid finite element/statistical energy analysis method[J].Journal of Sound and Vibration， 2014， 333(6)：1698-1717.

[11] 張瑾，馬興瑞，韓曾堯，等.中頻力學環境預示的FE-SEA混合方法研究[J].振動工程學報，2012，25(2)：206-214.

[12] WU F，HE Z C，LIU G R，et al.A novel hybrid ES-FE-SEA for mid-frequency prediction of transmission losses in complex acoustic system[J].Applied Acoustics， 2016， 111： 198-204.

[13] 楊熊偉，李躍明，耿謙.基于混合FE-SEA法的高溫環境飛行器寬頻聲振特性分析[J].航空學報，2011，32(10)：1851-1859.

[14] 林華剛，閆云聚，李鵬博.飛行器結構在高強寬頻噪聲環境下的響應預示分析與試驗研究[J].機械工程學報，2016，52(3)：71-78.

[15] 傅立敏.汽車設計與空氣動力學[M].北京：機械工業出版社，2011.

[16] 汪怡平，谷正氣，楊雪，等.汽車天窗風振噪聲數值模擬與控制[J].中國公路學報，2010，23(6)：108-114.

[17] 盧禮華，陸建輝，劉志峰，等.汽車坐盤安全氣囊對假人傷害的仿真及優化[J].西安交通大學學報，2016，50(9)：1-7.

[18] 高月華，張崎，王希誠.基于Kriging模型的汽輪機基礎動力優化設計[J].計算力學學報，2008，25(5)：610-615.

[19] 鄧召學，鄭玲，李以農，等.基于NSGA-Ⅱ算法的磁流變懸置磁路多目標優化[J].汽車工程，2015，37(5)：554-559.