兩個廣義伽瑪分布之間的相對熵及其性質

朱成蓮

0 引言

1951年,統計學家Kullback和Leibler提出了相對熵的概念，用來度量兩個分布之間的差異程度，也稱為Kullback-Leibler距離。在數理統計中,統計推斷的一個重要方面就是從已知樣本去估計母體的分布,或者推斷分布的特征,對于同樣的母體分布，當用幾種不同的統計方法獲得了母體的不同估計分布后,人們往往要對所求得的分布進行比較，為此，統計學上引入了許多度量兩個分布差異的方法，如相對熵，Pearson-χ2距離和全變差距離等，相對熵應用于許多領域，從相對熵的定義看出，它已經不滿足傳統的距離中對稱性、三角不等式性等條款。盡管如此，由于它確實能夠在某種程度上刻畫兩個密度函數的差異程度，近年來，概率密度函數的相對熵在學術界備受關注，人們在討論極值分布的大樣本問題、分布函數估計的收斂性、用不同算法借補有缺失數據的分布估計的收斂速度等問題時，都使用相對熵[1-5]。本文將相對熵定義進行了推廣，定義了最小相對熵。從定義形式上看，并不難理解，最小相對熵是將兩個概率密度函數間的相對熵求較小值，但它的意義在于克服了相對熵沒有對稱性的缺陷。本文計算了兩個廣義伽瑪分布之間相對熵及最小相對熵。作為廣義伽瑪分布的特例，推導出兩個伽瑪分布、Weibull分布、Rayleigh分布、正態分布、指數分布之間的相對熵及最小相對熵。

1 相關定義及其性質

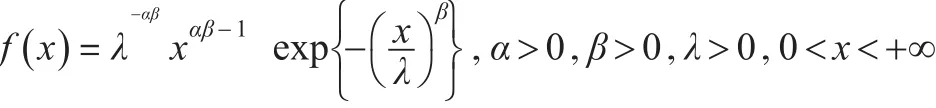
則稱隨機變量X服從廣義伽瑪分布,記為GΓ()α，β，λ。

由定義1可知，當α，β取一些特殊值時，得到以下一些特例：

定義1[6]：如果隨機變量X的概率密度函數為：

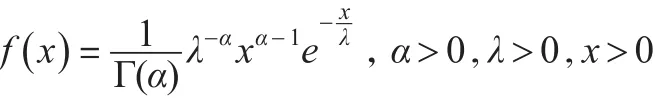
一般記為Γ(α，λ)。伽瑪分布中，若α為整數就是Erlang分布；伽瑪分布中，α=n（1）當β=1時，得到伽瑪分布,密度函數為：2，λ=2就是 χ2分布。（2）當α=1時，得到Weibull分布,密度函數為：

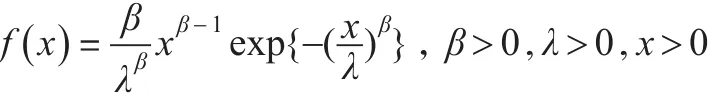
一般記為W(β，λ)。

（3）當 α=1，β=2，λ=2σ 時，得到 Rayleigh分布,密度函數為：

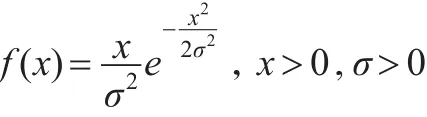
一般記為 R(σ)。

（4）當α=1，β=1時，得到指數分布，密度函數為：

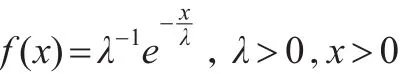
一般記為 E(λ)。

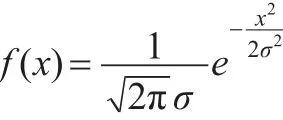
一般記為 N(0，σ2)。

定義 2[7]：設 f(x),g(x)是兩個密度函數,Sf和Sg分f(x) dx＜+∞時,則稱這個值是g(x)到f(x)的相對熵，又稱為Kullback-Leibler距離,記為d( f ，g )。

當f(x)，g(x)都是離散型隨機變量分布時，定義2中的積分需換成相應的求和記號。

定義3：設兩個隨機變量 X1，X2的概率密度函數分別為 f(x)、g(x)，并且 f(x)＞0，g(x)＞0，若 d( f ，g ) 和d(g，f)都存在，記 dmin(f，g)=min{d(f，g)，d(g，f)} ，則稱dmin(f，g)為 f(x)，g(x)兩個密度函數之間的最小相對熵。

由定義2和定義3易得以下有關相對熵的性質。

性質1：設 f(x)＞0，g(x)＞0是兩個概率密度函數，則：

（1）非負性 d(f，g)≥0

（3）d(f，g)=0?E(lnf(x))=E(lng(x))?f(x)=g(x)=0

（4）d(f，g1)-d(f，g2)=

從性質1的（1）、（3）知相對熵確實能刻畫兩個分布g(x)與Sf之間的差異程度，但是相對熵對稱性,三角形不等式未必成立。

性質2：設 f(x)＞0，g(x)＞0是兩個概率密度函數，

則：

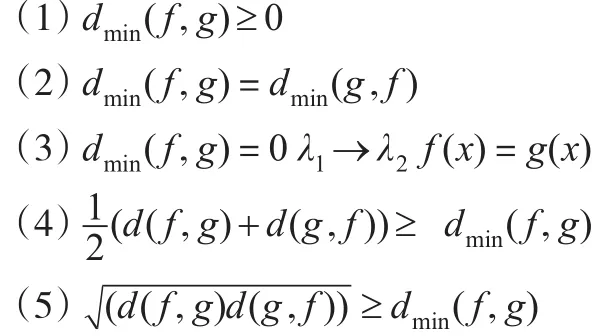
從性質2可以看出,最小相對熵與相對熵相比較,最小相對熵除了具有相對熵的性質外,還具有對稱性、三角不等式性質。

引理1：如果隨機變量X的概率密度函數為：

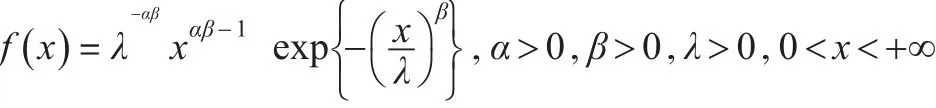
則：

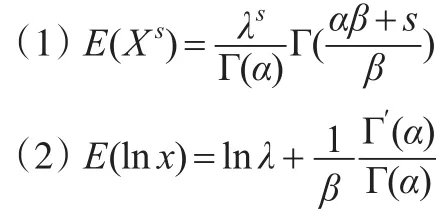
證明：計算積分

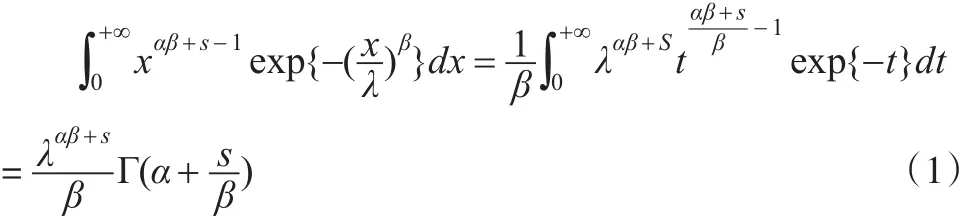
由式（1）可得隨機變量X的K階矩為：

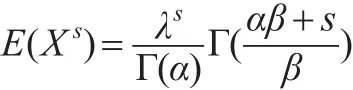
當式（1）中 s=0時，得到：

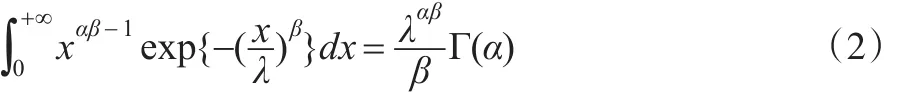
對式（2）兩邊關于α求導得：

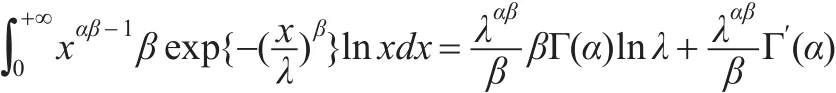
因此：

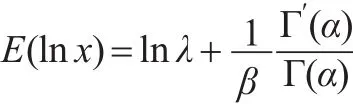
2 兩個廣義伽瑪分布之間的相對熵

定理 1：設 f(x)、g(x)分別是廣義伽瑪分布GΓ(α，β，λ1) 、GΓ(α，β，λ2)的密度函數,則：

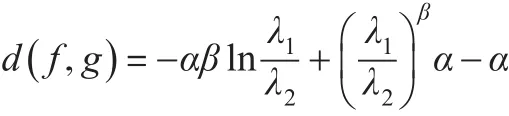
證明：根據定義2可得：

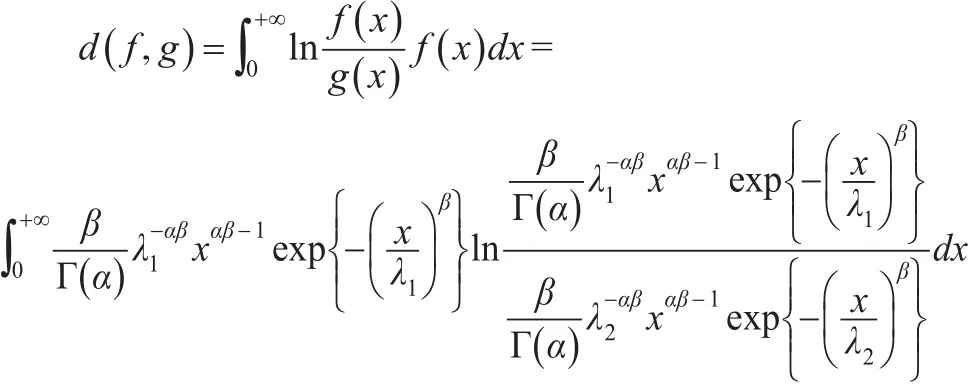
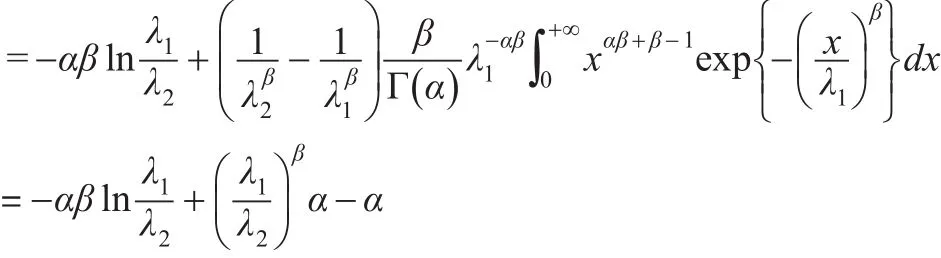
所以：

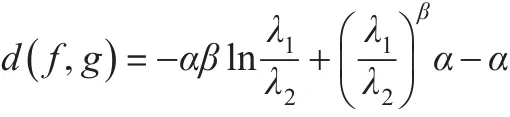
從上式可看出，當 λ1→λ2時，d(f，g)→0

定理 2：設f(x ) 、g(x)分別是廣義伽瑪分布GΓ(α，β，λ1) 、GΓ(α，β，λ2)的密度函數，則：

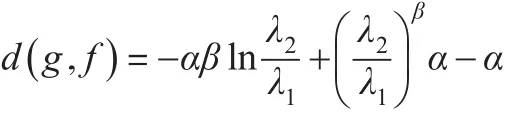
定理 3：設f(x ) 、g(x)分別是廣義伽瑪分布GΓ(α，β，λ1) 、GΓ(α，β，λ2)的密度函數，則：

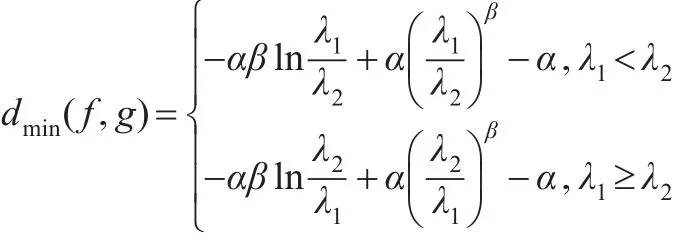
證明：由定理1和定理2可知：

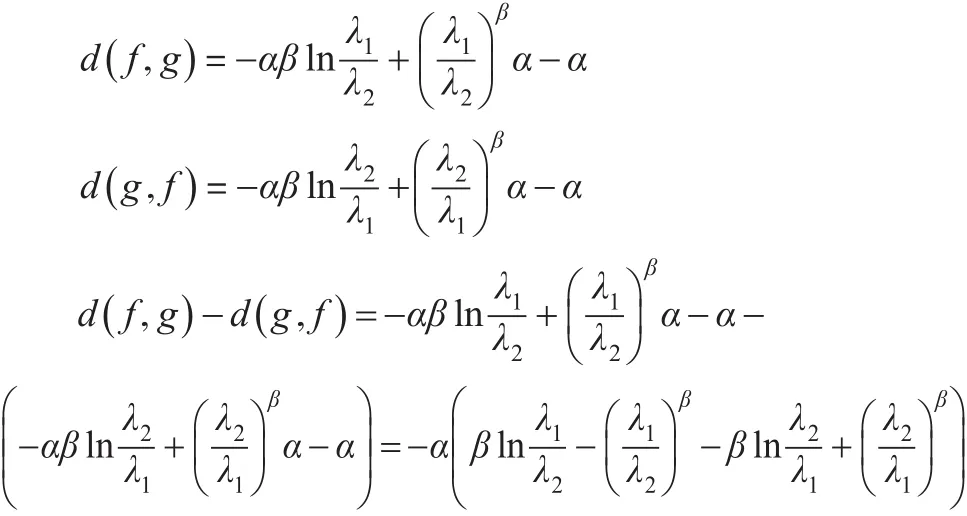
構造函數：

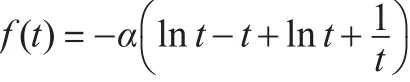
可得：

易知 f(t)為(0，+∞ )單調遞增函數。且當t=1時：

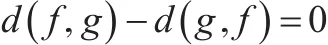
故：

因此：

且當 λ1→λ2時，d(f，g)→0 。

定理4：設 f(x)、g(x)分別是廣義伽瑪分布GΓ(α1，β，λ)、GΓ(α2，β，λ)的密度函數，則：′

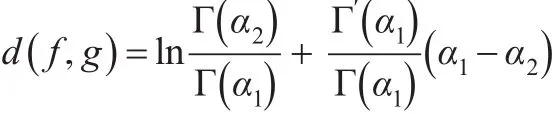
證明：根據相對熵的定義得：

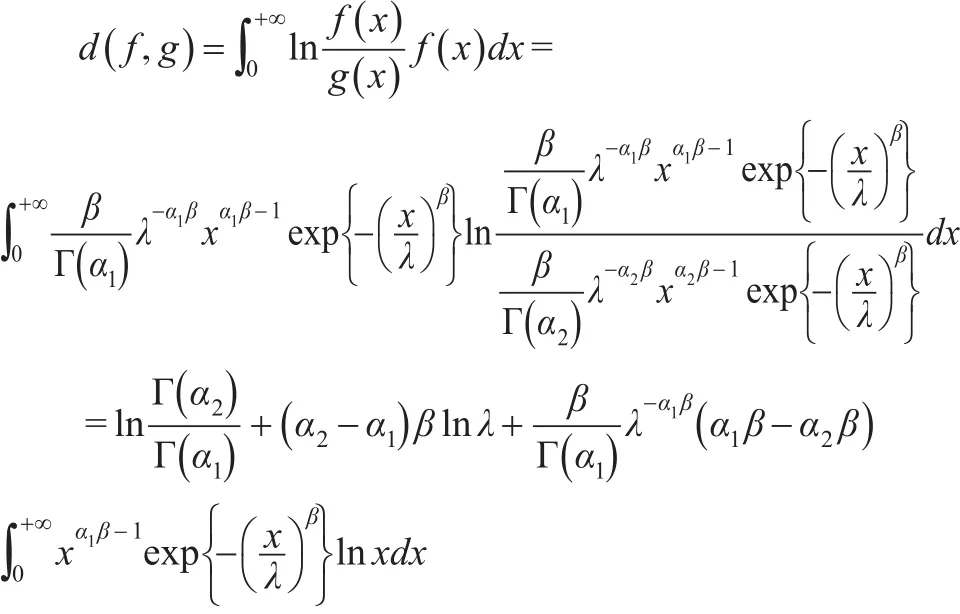
根據引理1結論可得：

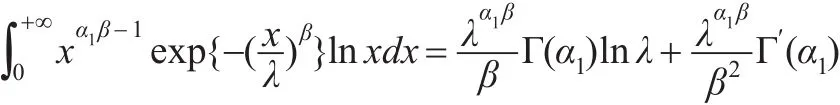
所以：

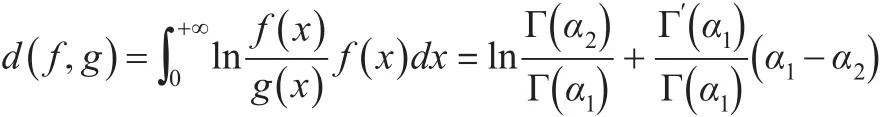
由上式可知，d( f ，g )與λ、β無關，兩個密度函數的相近程度由參數α決定，當α1→α2時，d( f ，g )→0。

定理 5：設 f(x)、g(x)分別是廣義伽瑪分布GΓ(α1，β，λ)、GΓ(α2，β，λ)的密度函數，當 β ，λ確定時，

且當α1→α2時，d( f ，g )→0。

定理 6：設 f(x)、g(x)分別是廣義伽瑪分布GΓ(α，β1，λ)、GΓ(α，β2，λ)的密度函數，當 α ，λ確定時，

證明：根據相對熵的定義可得：

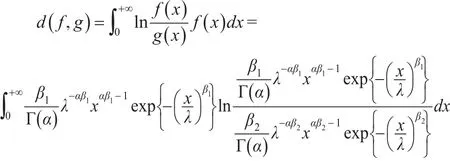
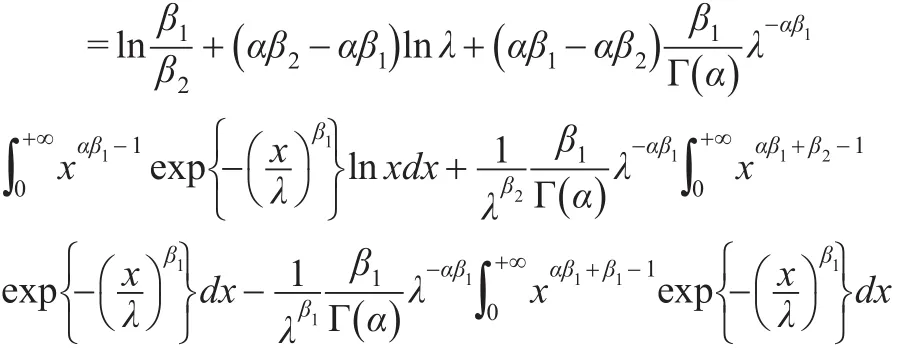
分別計算上式三個積分，根據引理1結論可得：

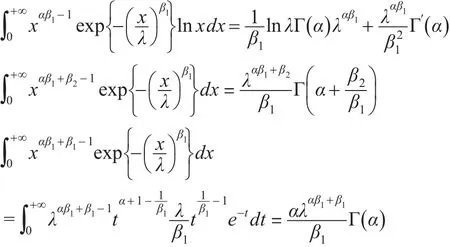
所以：

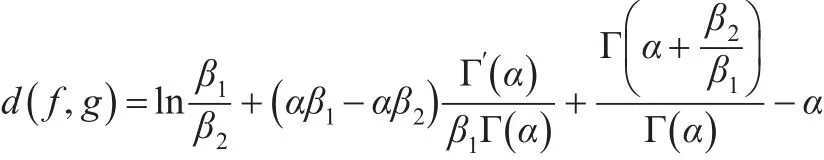
從上式可看出，d( f ，g ) 與 λ無關，當 β1→β2時，d(f，g)→0 。

定理 7：設f(x ) 、g(x)分別是廣義伽瑪分布GΓ(α，β1，λ)、GΓ(α，β2，λ)的密度函數,當 α ,λ確定時,則：

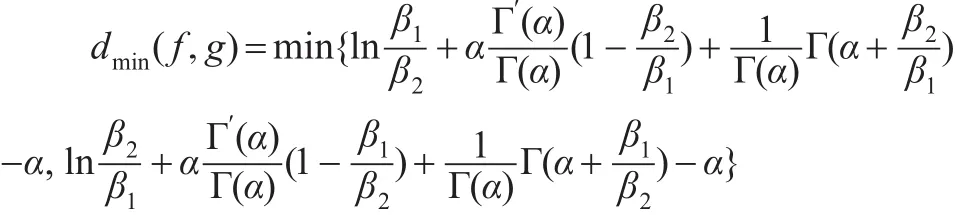
且當 β1→β2時，d(f，g)→0 。

由以上定理可得以下推論：

推論1：設 f(x)、g(x) 分別是伽瑪 Γ(α，λ1) Γ(α，λ2)的密度函數，則：

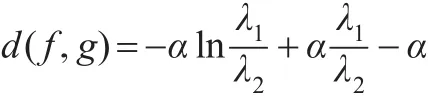
且當 λ1→λ2時，d(f，g)→0

推論2:設 f(x)、g(x) 分別是伽瑪 Γ(α，λ1) Γ(α，λ2)的密度函數,則：

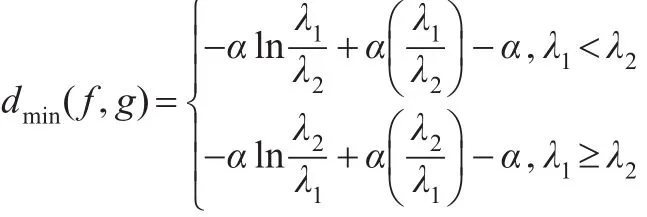
且當 λ1→λ2時，d(f，g)→0

推論3：設 f(x)、g(x )分別是Weibull分布W(β，λ1)、W(β，λ2)的密度函數，則：

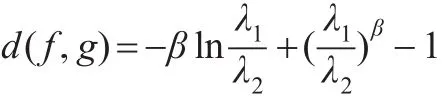
且當 λ1→λ2時，d(f，g)→0。

推論4：設 f(x)、g(x )分別是Weibull分布W(β，λ1)、W(β，λ2)的密度函數，則：

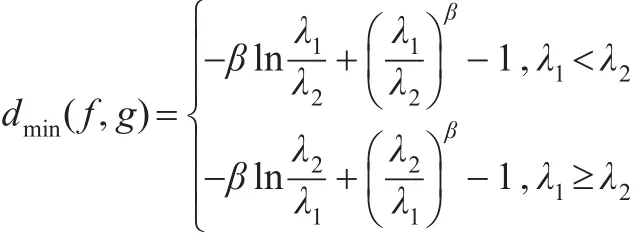
且當 λ1→λ2時，d(f，g)→0 。

推論5：設 f(x)、g(x) 分別是 Rayleigh分布 R(σ1)、R(σ2)的密度函數，則：

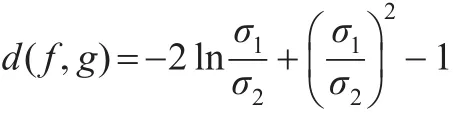
且當σ1→σ2時，d(f，g)→0。

推論6：設 f(x)、g(x) 分別是 Rayleigh分布 R(σ1)、R(σ2)的密度函數，則：

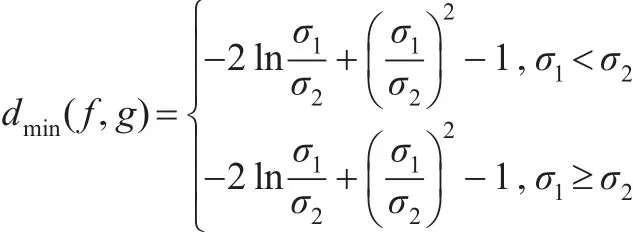
且當σ1→σ2時，d(f，g)→0。

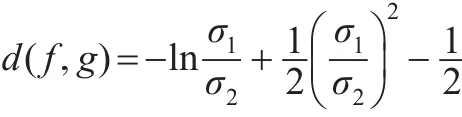
且當σ1→σ2時，d(f，g)→0。

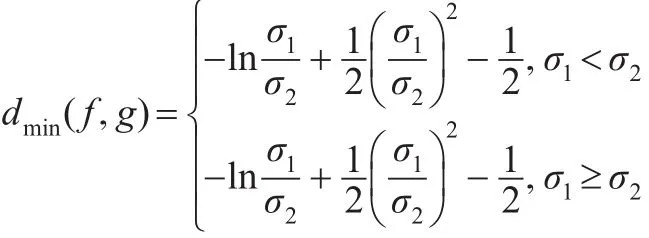
且當σ1→σ2時，d(f，g)→0。

推論9：設 f(x)、g(x) 分別是指數分布 E(λ1)、E(λ2)的密度函數，則：

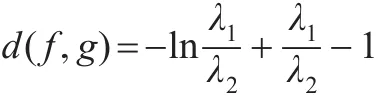
且當 λ1→λ2時，d(f，g)→0 。

推論10：設 f(x)、g(x) 分別是指數分布 E(λ1)、E(λ2)的密度函數，則：且當 λ1→λ2時，d(f，g)→0 。

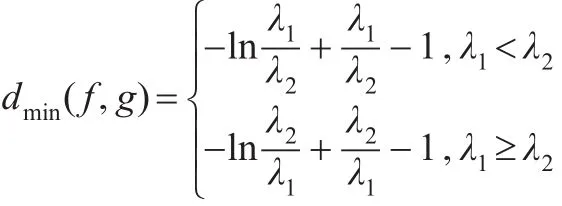
3 幾個距離間的關系

定義4［7］：設 f(x)，g(x)是兩個密度函數，Sf和Sg分離，記為 d2(f，g)。

定義 5［7］：設 f(x)，g(x)是兩個密度函數，稱V2(f，g)=suAp|F(A)-G(A)|是f(x)到g(x)的全變差距離，其中

定理8［7］：以下討論的距離都存在，則：

（1）當 f(x)≥g(x)時，d(f，g)≤d2(g，f)。

（2）V2(f，g)≤ d2(f，g)。

有 d(f，g)，d(g，f)及 min{d(f，g)，d(g，f)} 的定義易得如下定理。

定理9：若以下討論的距離都存在，則：

（1）min{d(f，g)，d(g，f)} ≤d(f，g)≤ max{d(f，g)，d(g，f)} ；

（2）當 f(x)≥g(x)時 d(f，g)≥d(g，f)，且 d(f，g)≥(d(f，g)+d(g，f))≥d(g，f) ；當f(x)≤g(x) 時 d(f，g)≤d(g，f)，且 d(f，g)≤(d(f，g)+d(g，f))≤d(g，f)。

從定理 9中的式（1）還可以看出，當 min{d(f，g)，d(g，f)}充分小時，必有d(f，g)充分小。用最小Kullback-Leibler距離min{d(f，g)，d(g，f)} 來比較兩個密度函數比用d(f，g)刻畫要合理。

4 結束語

相對熵用來度量兩個分布之間的差異程度，相對熵越小，表示兩個分布之間越接近，反之，相差越大，當兩個分布相同時，相對熵為零。本文計算了兩個廣義伽瑪分布之間的相對熵，得到了公式。根據參數的大小，非常容易度量兩個廣義伽瑪分布之間接近程度，或根據兩個廣義伽瑪分布之間接近程度的要求，由公式快捷選擇參數。從相對熵的定義看出，它不滿足傳統的距離中對稱性、三角不等式性等條款。本文定義了最小相對熵。從定義形式上看，并不難理解，最小相對熵是將兩個概率密度函數間的相對熵求較小值，但它的意義在于克服了相對熵沒有對稱性的缺陷。并且最小相對熵充分小時，必有相對熵充分小。用最小相對熵來度量兩個密度函數比用相對熵刻畫更為合理。本文還推導出兩個伽瑪分布、Weibull分布、Rayleigh分布、正態分布、指數分布之間的相對熵及最小相對熵。為實際應用，提供許多方便。

[1]Robert G O,Shau S K.Updating Schemes,Correlation Structure,Blocking and Parameterization for the Gibbs Sampler[J].J R Statist Soc B,1997,(59).

[2]Liu S J,Wong W H,Kong A.Correlation Structure and Convergence Rate of the Gibbs Sampler with Various Scans[J].J R Statist Soc B,1995,(57).

[3]Reiss R D.Approximate Distributions of Order Statistics[M].New York:Springer,1980.

[4]Whittaker J.Graphical Models in Applied Multivariate Statistics[M].Wiley:Chichester,1990.

[5]李開燦,孟朝玲.χ2分布、t分布和F分布的一致漸進正態性[J].北京印刷學院學報,2004,12(3).

[6]金秀巖.廣義Γ分布的Pearson-χ2距離及其漸近性[J].西南師范大學學報:自然科學版,2008,33(4).

[7]李開燦.Pearson-χ2距離的若干性質[J].數學的實踐與認識，2003,33（1）.