穩健總體最小二乘法一元線性回歸的相對有效性探討

劉清，葛永慧

0 引言

線性回歸模型是用于解決數理統計問題中變量之間關系的常規模型，最小二乘法是求解其回歸系數最經典的方法。最小二乘法在求解回歸系數時只考慮線性回歸模型中觀測值含隨機誤差的情況，總體最小二乘法（TLS）是為了顧及觀測值和系數矩陣同時含有隨機誤差的狀況。然而無論是最小二乘法還是總體最小二乘法都不具有抵抗粗差的能力，當觀測值或系數矩陣中包含粗差時，參數估計的結果將會被歪曲[1]。

由于測量人員的工作疏漏以及儀器精密度不同等各種主觀因素，數據采集過程中粗差會不可避免地出現。為了剔除或減弱粗差對參數估計的影響，在回歸分析中應用穩健估計原理，定義穩健回歸的理念。RLS法僅能顧及誤差方程中觀測向量含粗差的情況，因此，在RLS法的基礎上提出了RTLS法——作為一種可顧及系數矩陣和觀測向量中涉及粗差的參數估計方法被提出。一些學者將RTLS法引入到線性回歸模型中，并通過個別算例中RTLS法得到比RLS法更小的單位權中誤差和精度較高的參數解，從而得出在線性回歸中RTLS法比RLS法更為有效的結論。

穩健最小二乘法（RLS）的研究已取得了大量的研究成果[2]，穩健總體最小二乘法（RTLS）的研究也取得了一些成果。楊娟等[3]同樣把基于穩健估計的TLS法應用于GPS高程異常擬合問題，指出基于穩健估計的TLS法能更好地解決GPS高程擬合模型中控制點已知坐標含誤差的問題。陳瑋嫻等[4]提出了穩健總體最小二乘方法為了解決誤差模型中觀測值含有粗差的狀況，并以小角度坐標轉換得出當兩套坐標均含隨機誤差且未含粗差時TLS法優于LS法，當兩套坐標均含隨機誤差且觀測值同時受粗差影響時RTLS法優于TLS法。汪奇生等[5]針對線性回歸中自變量和因變量可能含有粗差的情況，提出線性回歸模型的穩健總體最小二乘算法，并以一元線性回歸為例，得出RTLS法較LS法、TLS法、RLS法能更有效地剔除粗差。

迄今為止，并沒有明確的理論研究說明在一元線性回歸中RTLS法的相對有效性，如果僅僅通過特殊或極個別算例就論證在線性回歸中穩健總體最小二乘法一定優于穩健最小二乘法太過片面，并不足以讓人信服。其次，判斷兩種參數估計方法的相對有效性的比較指標應選取均方誤差，并不能簡單地以單位權中誤差來衡量精度。基于上述分析，為了更精確地進行測量數據處理和后續理論的研究指導，對穩健總體最小二乘法在一元線性回歸中的相對有效性加以分析研究，仍具有一定的迫切性和必要性。

1 模型分類和方法

1.1 線性回歸誤差影響模型的分類

測量數據不可避免地會受隨機誤差和粗差的影響，當運用不同的參數估計方法或建立不同的函數模型時，使得不同的測量數據在參數估計模型中所起的作用也不相同。因此，對一元線性回歸中觀測值和系數矩陣受粗差和隨機誤差不同影響的變化情形下，劃分為三種不同的誤差影響模型，如下：

模型1：此誤差影響模型中僅觀測值含有隨機誤差和粗差，系數矩陣不含隨機誤差和粗差。即線性回歸模型中體現為僅因變量含隨機誤差和粗差。

模型2：此誤差影響模型中僅觀測值含隨機誤差，系數矩陣含隨機誤差和粗差。即線性回歸模型中體現為自變量含隨機誤差和粗差，因變量僅含隨機誤差。

模型3：此誤差影響模型中觀測值含隨機誤差和粗差，系數矩陣僅含有隨機誤差。即線性回歸模型中體現為因變量含隨機誤差和粗差，自變量僅含隨機誤差。

1.2 穩健估計方法

6種常用的穩健估計方法如下[2]：

（1）Huber法：

（2）L1法（殘差絕對和最小法）：

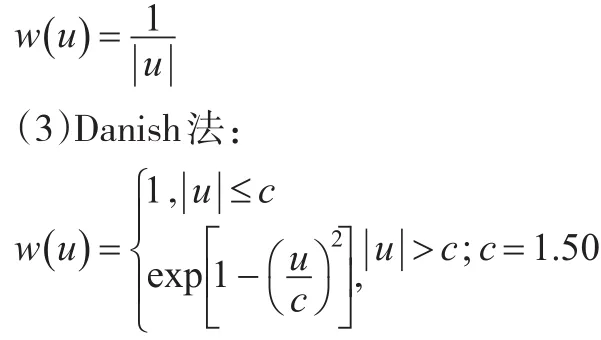
（4）German-McClure法：

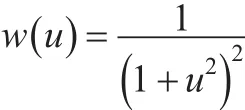
（5）IGG方案：

（6）IGGⅢ方案：

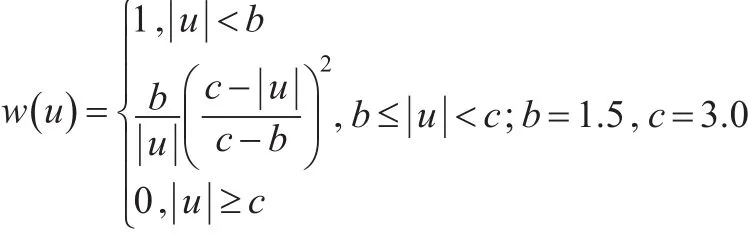
1.3 比較參數估計方法的指標[2]

（1）殘余真誤差均方誤差（參數估計的絕對指標）

其中，設觀測值為Lk；觀測值真值由L?k表示；由參數估計方法獲得的Lk的估值由L?k表示；Lk的真誤差由Δk表示；由參數估計方法獲得的Lk的改正數由Vk表示。其

殘余真誤差均方誤差（Mean Square of Residual True Error），由MSRTE表示：

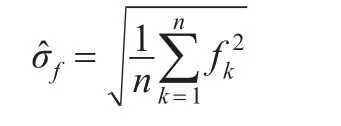
σ?f為殘余真誤差均方誤差，此指標能從根本上將參數估計方法的優劣性和有效性進行實質說明。用統計學的思想對比兩種參數估計方法的相對優劣性和相對有效性，針對同一個參數估計問題，相同參數估計方法進行1000次仿真實驗所獲取的MSRTE的平均值定為殘余真誤差均方誤差[6]，由σ?f來表示。

（2）參數估計的MSRTE之比（相對指標）

在同一參數估計問題中，σ?fa表示由方法A得到的MSRTE，σ?fb表示由方法B得到的MSRTE，令：

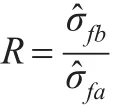
R稱為殘余真誤差均方誤差比。式中，是A方法得到的MSRTE，是B方法得到的MSRTE。當R＞1.0時，A方法優于B方法；當R＜1.0時，B方法優于A方法;當R趨向于1.0時，A和B兩種方法等價。R作為能從實質上對兩種參數估計有效性根本說明的指標存在。繼而，運用統計學的思想對兩種參數估計方法的相對有效性進行說明，和通常是指A、B兩種參數估計方法對于同一個參數估計問題仿真實驗多次（如1000次）的平均值。

在本文中，RTLS法得到的觀測值（回歸系數）估值的殘余真誤差均方誤差與RLS法得到的觀測值（回歸系數）估值的MSRTE之比用指標RR特指，從根本上說明在一元線性回歸中，穩健最小二乘法和穩健總體最小二乘法的相對有效性。

2 算例、實驗與討論

2.1 算例

一元線性回歸模型的理論方程為：

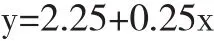
從區間[10,37]中任意選取10個均勻分布的數為x，并通過上述方程獲取真值Y?i，組成10對點作為理論模擬值。由模擬觀測真值Y?i、x，在三種不同誤差影響模型下，加上包含粗差ε=10σ0、其余服從正態分布N(0，0.12)的隨機誤差得到相應的模擬觀測值yi、xi。

以穩健估計Huber法計算結果為例，運用RLS法和RTLS法分別進行參數估計運算，得出觀測值的改正數V、觀測值估值的殘余真誤差以及回歸系數估值a?0、a?1和回歸方程，并通過觀測值估值的殘余真誤差fk計算觀測值估值的MSRTE以及通過回歸系數估值a?0、a?1計算回歸系數估值的殘余真誤差。其中，RTLS具體計算步驟參照文獻[5]。三種誤差影響模型下RLS法和RTLS法的模擬觀測數據和實驗結果見表1。觀測值（因變量）真值由Y?i表示，其中元數由i表示，i=1，2，3。x表示自變量真值，Δ表示服從正態分布N(0，0.12)的隨機誤差，y表示由Y?i和隨機誤差Δ、粗差ε=10σ0共同生成的模擬觀測值。RLS法的觀測值改正數由VA表示，RLS的殘余真誤差由△A表示。RTLS的觀測值改正數由VB表示，RTLS的殘余真誤差由△B表示。

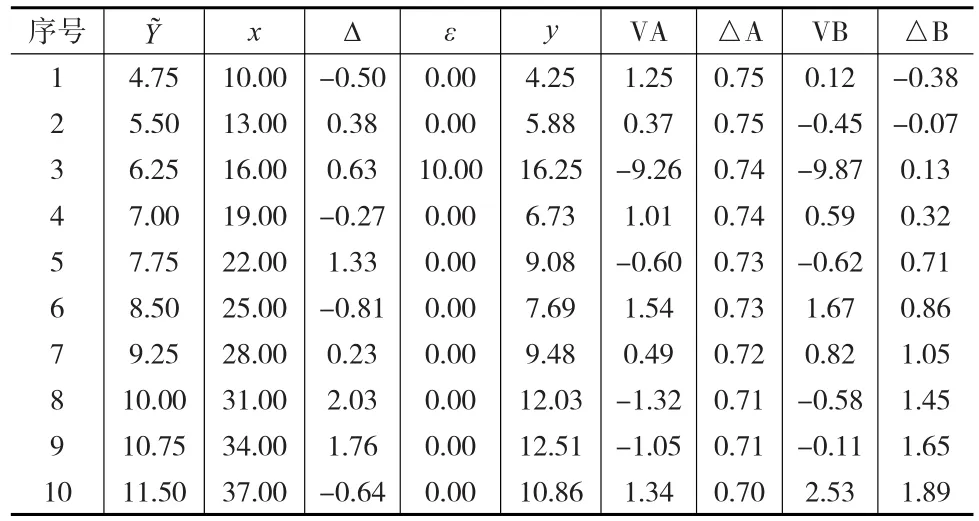
表1 模擬觀測值和真值與RLS法和RTLS法的實驗結果

由RLS 法計算得到的回歸系數估值a?0=3.0233，a?1=0.2481。回歸方程：

由表1中△A列數據可計算得到RLS法觀測值估值y?的MSRTE為：σ?f1=0.73。

RTLS 法 得 到 的 回 歸 系 數 估 值a?0=1.0436，a?1=0.3338。回歸方程：

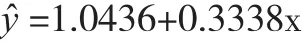
由表1中△B數據得到的RTLS法的y?的MSRTE為：σ?f2=1.05 。

觀測值估值y?的RTLS法和RLS法的殘余真誤差均方誤差比：

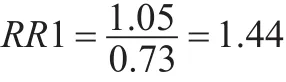
通過一次計算就可以獲得觀測值估值y?的MSRTE，對于仿真1000次實驗計算，取其平均值作為觀測值的MSRTE。

由RLS法計算得到回歸系數估值a?0的殘余真誤差為Δ3=a?0-a?0=0.7733 ，回歸系數估值a?1的殘余真誤差為Δ4=a?1-a?1=-0.0019 。

回歸系數估值a?0通過RTLS法得到的殘余真誤差為Δ3=a?0-a?0=-1.2064 ，回歸系數估值a?1的殘余真誤差為Δ4=a?1-a?1=0.0838 。

回歸系數估值的殘余真誤差可以通過一次仿真實驗計算出，其殘余真誤差均方誤差可由1000次的仿真實驗計算出。

2.2 一元線性回歸的仿真實驗

當給定a?0、a?1和自變量x的取值時，就可通過一元線性回歸的理論模型y?=a?0+a?1x得到理論模擬值，通過運用三種不同誤差影響模型，由理論觀測值加上隨機誤差或粗差生成模擬觀測值。

選取三組不同斜率的一元線性回歸方程：A組、B組、C組，分別為斜率約為tan15°、tan45°、tan75°的一元線性回歸模型，相對應的理論回歸方程為：y?=2.25+0.25x、y?=2.25+1.05x、y?=2.25+3.75x。

在上述A、B、C三組方程中分別根據三種不同誤差影響模型、不同穩健估計方法在觀測值n=6(n表示觀測值個數)的情形下進行仿真實驗。

以觀測值n=6為例，由上述三種不同斜率（tan15°、tan45°和tan75°）的一元線性回歸模型生成的理論模擬值見表2。

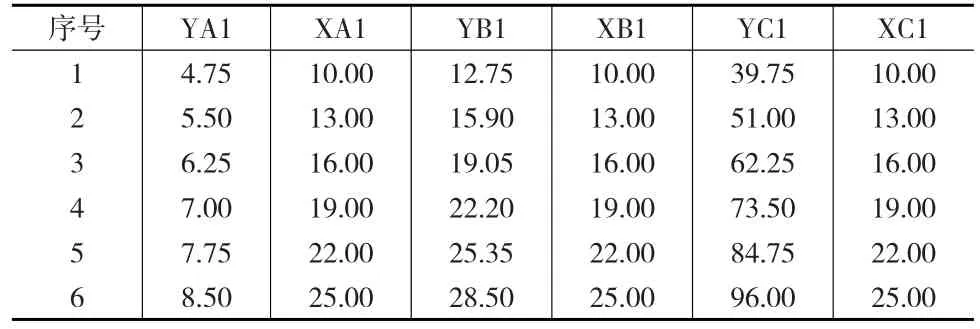
表2 不同斜率的理論模擬值（n=6）

理論模擬值加上隨機誤差或粗差（ε=10σ0）生成模擬觀測值。對于觀測值n=6、三種不同的斜率、三種不同誤差影響模型的情形分別進行1000次仿真實驗（方法同算例2.1）。

n=6，ε=10σ0時RLS和RTLS得到的觀測值估值y?的殘余真誤差均方誤差見表3，由表3可計算得RTLS與RLS觀測值估值y?的殘余真誤差均方誤差之比見表4，回歸系數的估值a?0和a?1通過RTLS和RLS所獲得的MSRTE之比見表5。

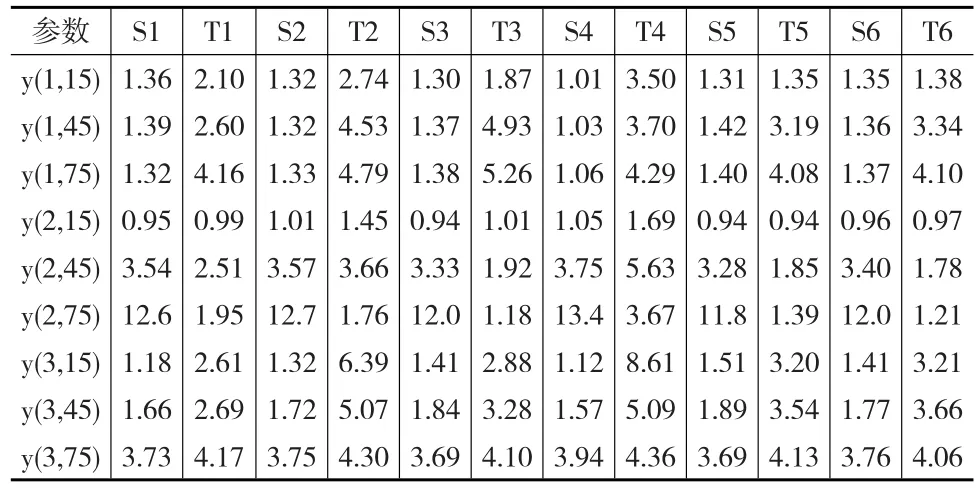
表3 RLS和RTLS的觀測值估值y?的殘余真誤差均方誤差(n=6，ε=10σ0)

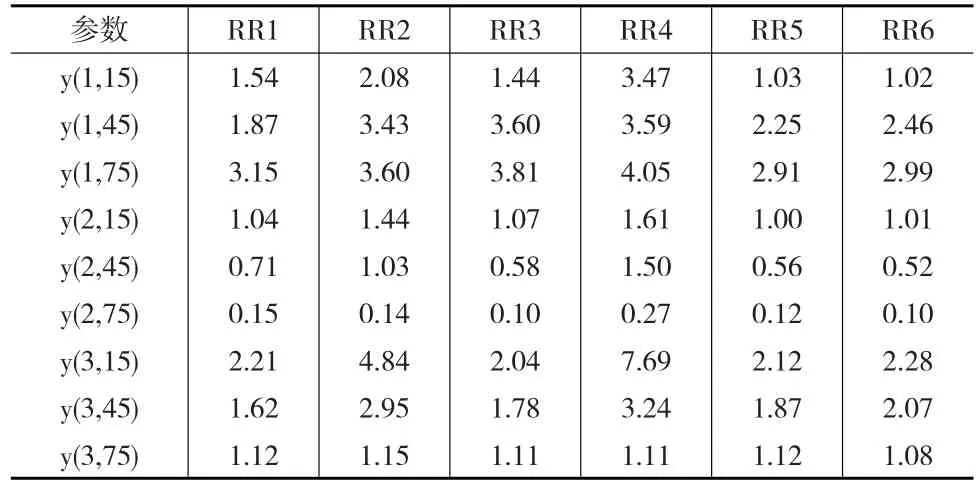
表4 RTLS和RLS的觀測值估值 y?的MSRTE之比(n=6，ε=10σ0)

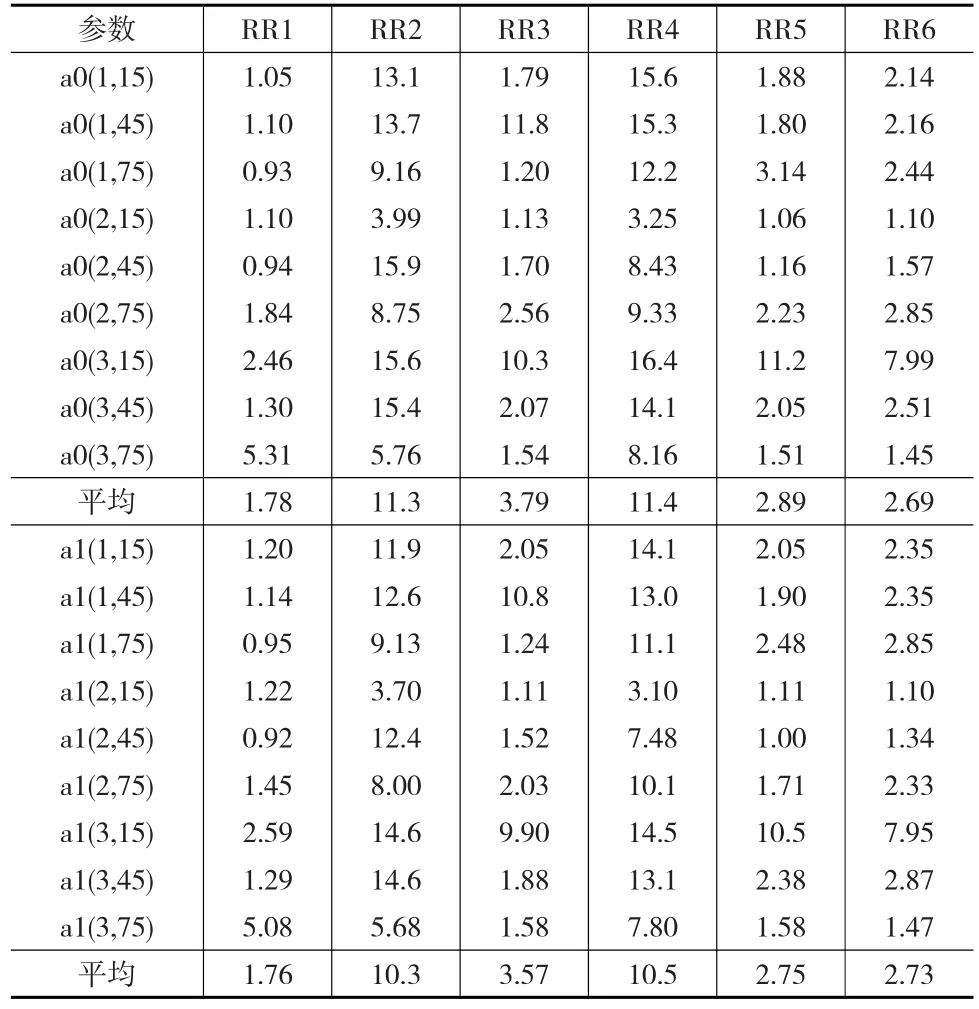
表5 RTLS和RLS的回歸系數的估值a?0和 a?1MSRTE之比 (n=6，ε=10σ0)

（1）第一種誤差影響模型（僅觀測值（因變量）含有粗差和隨機誤差）

對于A、B、C三組不同斜率（tan15°、tan45°和tan75°）以及觀測值（因變量）含有粗差和隨機誤差的情況，通過RLS和RTLS發現所得到的觀測值估值y?的殘余真誤差均方誤差之比（表4）都有RRi＞1.0；RTLS和RLS得到的回歸系數的估值 a?0和 a?1的殘余真誤差均方誤差之比（表5）是絕大多數情況下RRi＞1.0和個別情況下RRi接近1.0。所以RLS無論是對于觀測值估值y?還是對于回歸系數的估值a?0和 a?1相對于RTLS都更有效。

（2）第二種誤差影響模型（系數矩陣含有隨機誤差和粗差，觀測值僅含有隨機誤差的）

對于6種常用的相對有效穩健估計方法，RTLS和RLS在斜率約為tan15°時，所獲得的觀測值估值y?的殘余真誤差均方誤差之比（表4）是絕大多數情況下RRi＞1.0和個別情況下RRi接近1.0，RLS相對于RTLS更有效；RTLS和RLS在斜率約為tan45°時，所獲得的觀測值估值 y?的殘余真誤差均方誤差之比（表4）1.50＞=RRi＞=0.52，RLS和RTLS有效性很難被說明；RTLS和RLS在斜率約tan75°時，所獲得的觀測值估值y?的殘余真誤差均方誤差之比（表4）有 RRi＜=0.27；RTLS相對于RLS更有效。

對于（tan15°、tan45°和tan75°）這三種不同的斜率以及6種常用的相對有效的穩健估計方法而言，通過RTLS和RLS計算獲取的回歸系數估值 a?0和 a?1的MSRTE之比（表5）在絕大多數情況下RRi＞1.0和個別情況下RRi接近1.0。RLS 對于回歸系數的估值 a?0和 a?1比 RTLS 更為有效。

（3）第三種誤差影響模型（觀測值含有隨機誤差和粗差，系數矩陣僅含有隨機誤差）

對于A、B、C三組不同斜率（tan15°、tan45°和tan75°）以及6種常用的相對有效的穩健估計方法而言，RTLS和RLS得到的觀測值估值 y?的殘余真誤差均方誤差之比（表4）是絕大多數情形下RRi＞1.0和個別情況下RRi接近1.0；RTLS和RLS得到的回歸系數的估值 a?0和a?1的殘余真誤差均方誤差之比（表5）都有RRi＞1.0。即無論是觀測值估值 y?還是回歸系數的估值 a?0和 a?1，RLS相對于RTLS更有效。

利用類似的方法，對和n=10和ε=10σ0的情形進行了類似的仿真實驗，所得到的結果與ε=10σ0和n=6的情形相同。

3 結論

本文用不同的誤差（粗差）影響模型、不同的穩健估計方法和不同的斜率，運用仿真實驗的方法，討論了一元線性回歸中RLS法和RTLS法的相對有效性。

針對A、B、C三組（斜率約為tan15°、tan45°和tan75°）的一元線性回歸模型：就觀測值（因變量）的估值而言，在第一種和第三種誤差影響模型下，RLS優于RTLS。在第二種誤差影響模型下，當斜率較小（約tan15°）時，RLS比RTLS相對更為有效；當斜率約為tan45°時，難以說明RTLS與RLS哪個更有效；當斜率較大（約tan75°）時，就RLS而言RTLS相對更為有效。在三種不同的誤差影響模型下，針對回歸系數的估值而言，RLS始終都比RTLS相對更為有效。因此，綜上所述，對于一元線性回歸RTLS相對于RLS并沒有明顯的優越性。

[1]孫同賀，閆國慶，周強波.穩健初值的選權迭代法剔除DEM數據粗差[J].測繪科學，2011,36(3).

[2]葛永慧.再生權最小二乘法穩健估計[M].北京：科學出版社，2015.

[3]楊娟，陶葉青.GPS高程異常擬合的文件總體最小二乘算法[J].大地測量與地球動力學，2014,34(5).

[4]陳瑋嫻，袁慶.抗差總體最小二乘方法[J].大地測量與地球動力學，2012,32(6).

[5]汪奇生，楊德宏，楊騰飛.線性回歸模型的穩健總體最小二乘解算[J].大地測量與地球動力學，2015,35(2).

[6]葛永慧.再生權最小二乘法研究[J].測繪通報,2014,(8).