回歸系數變點估計的快速非迭代抽樣算法
楊豐凱,袁海靜
0 引言
變點問題是指在一隨機序列中存在某一時刻,使得該時刻兩側的序列服從不同的分布。
從上世紀50年代開始,估計一隨機序列中變點的位置成為統計學中的研究熱點之一,Chen等[1]詳細介紹了各種變點模型及其在遺傳學、醫藥以及金融領域的應用。其中一類問題是研究如何有效地估計線性回歸模型中回歸系數的變點位置,該類問題可描述為:對于序列yi,i=1,…n, 存在位置 r,p≤r≤n-p,使得:
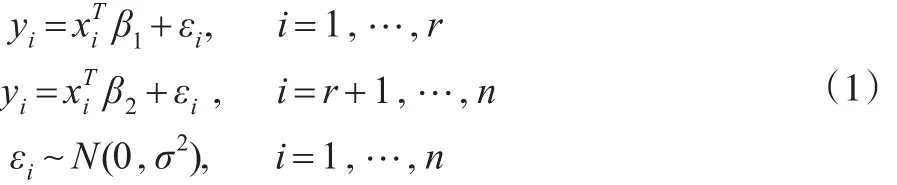
且 εi,i=1,…,n 相 互 獨 立 。 其 中 xi=(1,xi1,…xi,p-1)T,β1,β2為不同的 p 維回歸系數。本文的目標是估計變點位置r。對于該類問題,文獻中的研究方法多是基于似然的方法和貝葉斯方法。其中,Quandt[2,3]發展了基于最大似然估計和似然比檢驗的回歸系數變點檢驗和估計方法,Kim等[4,5]研究了回歸系數變點似然比檢驗的漸進性質。 Ferreira[6],Chin Choy 和 Broemeling[7],Holbert[8]則詳細討論了回歸系數變點估計的貝葉斯方法。Chen等[1,9]則從信息論的角度,提出了基于Schwarz信息準則的變點估計方法。基于馬氏鏈蒙特卡洛(MCMC)的Gibbs抽樣,由于其靈活性和易實施性,是一種有效的貝葉斯變點估計方法,但Gibbs抽樣是一種迭代抽樣算法,所抽取的馬氏鏈是否收斂到后驗分布很難判斷,并且所抽取的樣本也很難保證是獨立的。Tian等[10]發展了一種基于逆貝葉斯公式的非迭代抽樣算法,稱為IBF抽樣,該算法能夠直接從離散的后驗分布中抽取獨立同分布的樣本,然后依據該樣本對相關參數做統計推斷,從而巧妙地避開了Gibbs抽樣的不足之處。Tian等[11]將IBF抽樣算法應用到變點問題的研究中,并討論了泊松變點在醫學數據中的應用。Yang等[12]則研究了正態分布均值變點的IBF抽樣算法。本文基于Yang等[12]的研究,將IBF算法應用到模型(1)中,討論估計回歸系數變點位置的非迭代抽樣算法。分別在弱先驗信息和共軛先驗信息下給出相應變點位置的精確后驗分布,用IBF獲得獨立同分布的樣本,并作相應的統計推斷,大量模擬結果顯示,該算法能夠有效地估計變點位置,并且算法的運行速度比迭代的Gibbs抽樣要快很多。
1 無信息先驗下正態回歸均值變點估計的IBF算法
本文在無信息先驗分布下討論回歸系數變點估計的非迭代抽樣算法。記 y=(y1,…,yn)T,模型(1)的似然函數為:
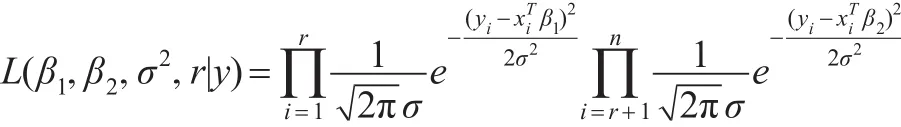
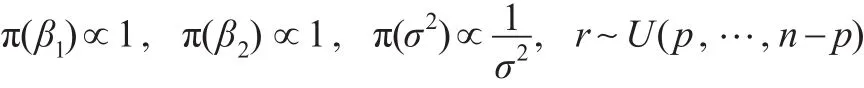
且 β1,β2,σ2,r 相互獨立。 其中 U(p,…,n-p)表示 p~(n-p)上的離散均勻分布,“∝”為正比符號。
1.1 無信息先驗下的條件分布
參數 (β1,β2,σ2,r)的聯合后驗分布:
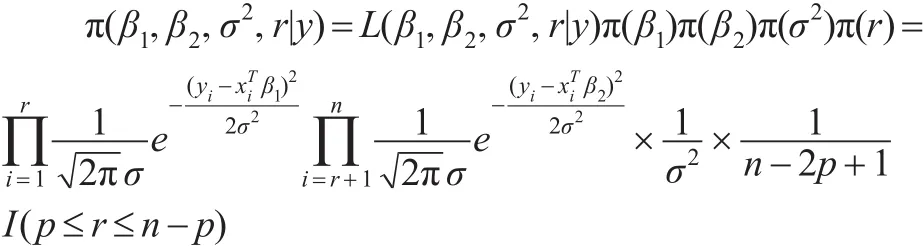
取如下無信息先驗分布:
從而變點位置r的條件后驗分布為:

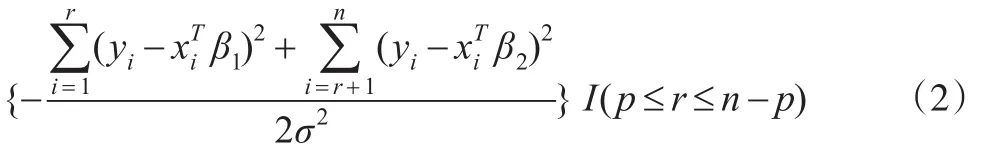
而:
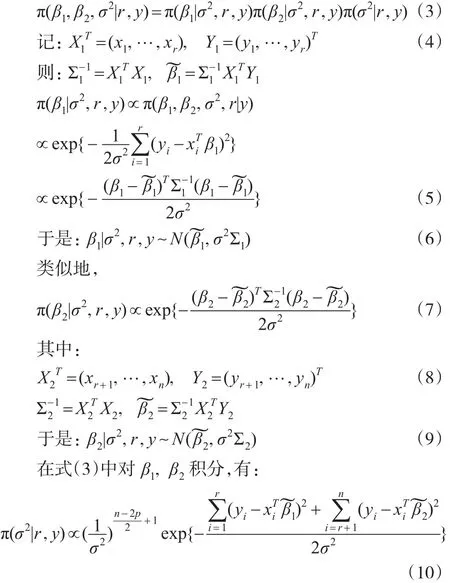
上式右端為逆伽馬分布的密度的核,故有:
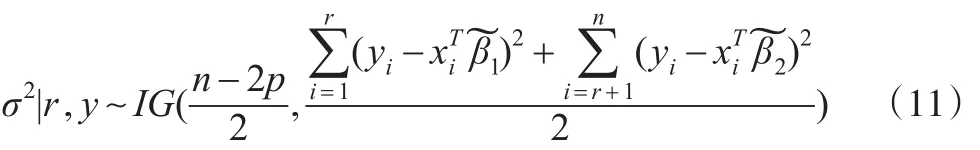
其中 IG(a,b)表示參數為a,b的逆伽馬分布。
1.2 IBF算法
根據Tian等[10,11]所提出的離散缺失數據分析的IBF算法的思想,有:
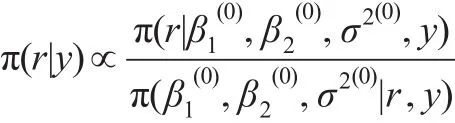
IBF抽樣算法分以下幾步:
第一步:計算
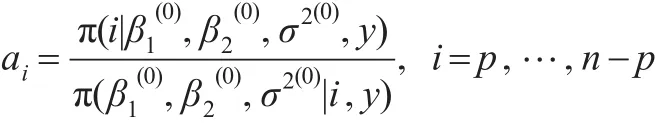
則變點位置r的精確后驗分布為:
P(r=i|y)=λi,i=p,…,n-p
第二步:以概率 λ=(λp,…,λn-p)從集合 S={p,…,布π(r|y)的獨立同分布的樣本,可以根據該樣本對r作統計推斷。
第三步:對 l=1,…,L,根據式(11)、式(6)和式(9),分別產生:
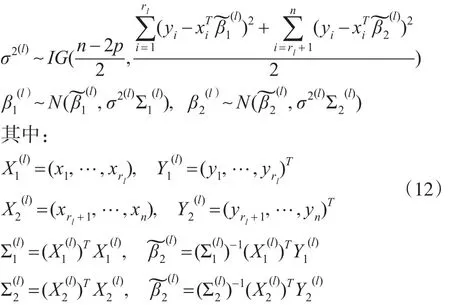
2 共軛先驗下正態回歸均值變點估計的IBF算法
在共軛先驗下研究正態回歸均值變點估計的IBF算法,取如下先驗分布:
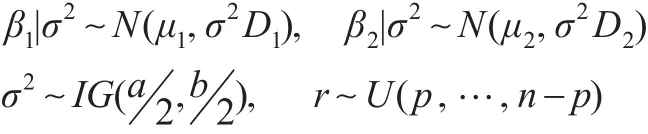
其中μ1、μ2均為 p維常向量,D1、D2均為 p階正定陣,IG(a2,b2)表示參數為a2和b2的逆伽瑪分布。在此假設 β1,β2關于 σ2條件獨立,且 (β1,β2,σ2)與 r 相互獨立。
2.1 共軛先驗下的條件分布
參數 (β1,β2,σ2,r)的聯合后驗分布:
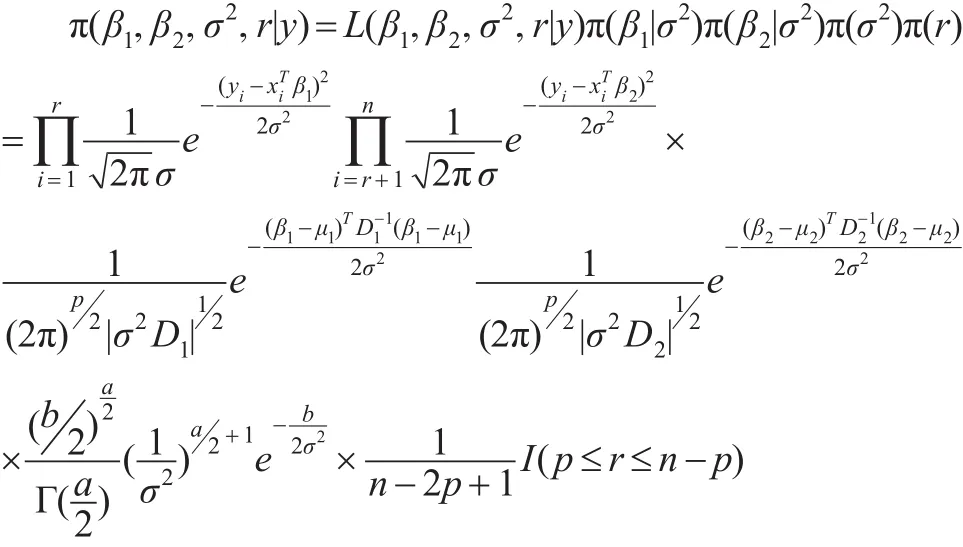
從而變點位置r的條件后驗分布為:
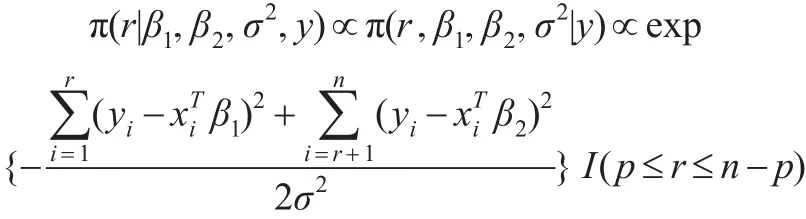
該分布與式(2)相同,與先驗分布的選取無關。而:
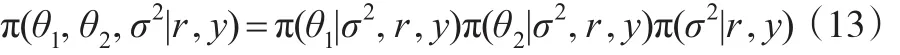
分別計算上式等號右端的三個條件分布。易見:

2.2 IBF算法
類似無信息先驗下的IBF算法,有:
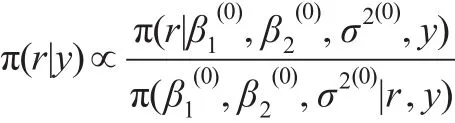
步驟3:對l=1,…,L,根據式(19)、式(15)和式(17),分別產生:
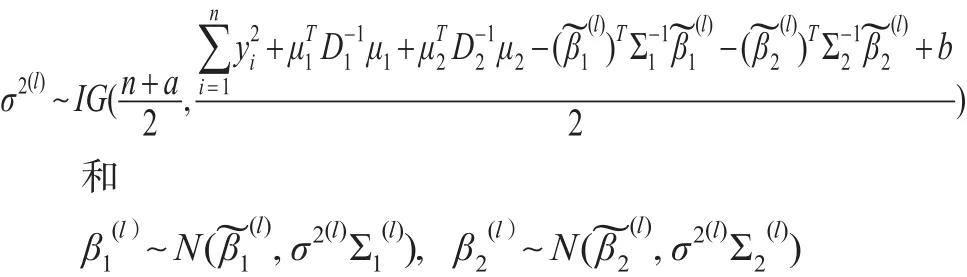
其中:
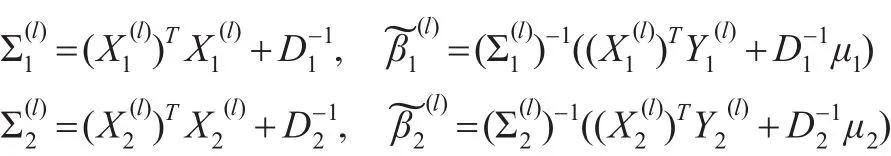
3 模擬
通過模擬,研究用IBF算法估計回歸系數變點位置的效果,并與迭代的Gibbs抽樣算法作比較。考慮如下單變點一元線性回歸模型:
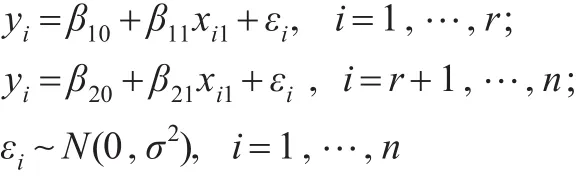
假設εi,i=1,…,n相互獨立。在此取n=200,β10=選取變點位置r=40,60,80,100,120 , 140,160。重復試驗200次,在每次實驗中分別實施IBF算法和Gibbs抽樣算法對變點位置進行估計。在第i次試驗中,記:
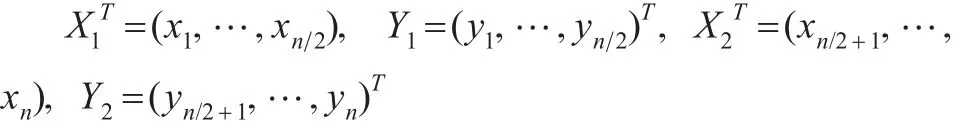
分別取前一半數據和后一半數據所得最小二乘估計作為初值,即有:

取σ2(0)=1。在Gibbs抽樣中,取r(0)=100。采取基于樣本的共軛先驗分布,其中:
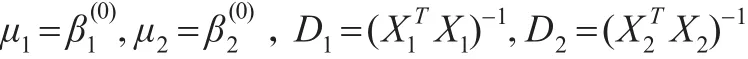
分別模擬產生變點位置r的L=6000個IBF樣本和L=6000個Gibbs樣本,并舍去前3000個作為burn-in樣本,方誤差的平方根(RMS)來衡量估計的精度,即有:
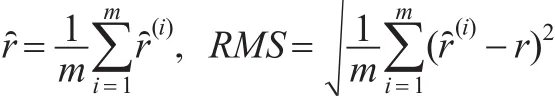
模擬結果如表1所示。

表1 對不同的變點位置,兩種算法的結果比較
表1顯示不論真實變點在何位置,兩種算法所得估計r?都很接近真實變點位置,并且估計的精度RMS都很小,說明兩種算法對真實的變點位置不敏感,都能夠有效地估計變點位置,并且兩種算法所得估計r?以及估計的精度RMS相差微乎其微。
比較對于產生相同的樣本量的兩種算法的計算時間。以r=80為例,本文取J分別為200,400,800,1000,3000,6000,10000,20000。共做200次重復試驗,這200次試驗的平均運行時間time(s)及r的估計r?和均方誤差的平方根(RMS)見表2。
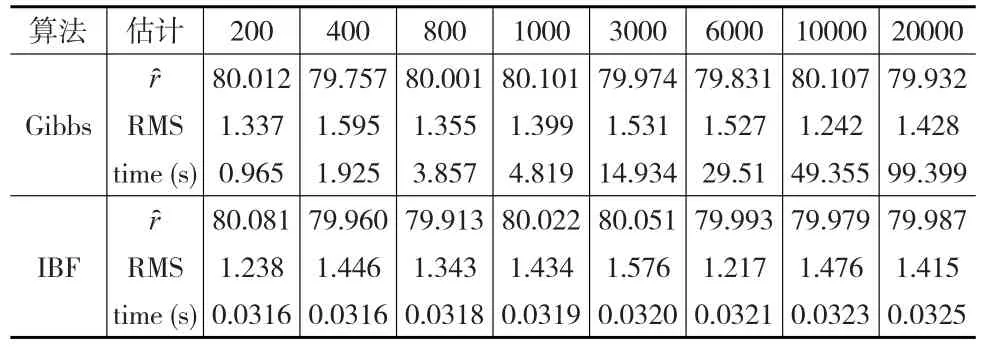
表2 對不同的樣本量兩種算法的結果比較
從表2可以看出,對不同的樣本量,兩種算法所得變點位置的估計值都很接近真值,所得估計的RMS都很小,說明這兩種算法都很有效。但兩種算法所產生相同樣本量的運行時間卻相差很大。當J從200增加到20000時,200次試驗中IBF算法的平均運行時間在0.0316秒到0.0325秒之間,相差只有0.0009秒,變化微乎其微;與之對比,Gibbs抽樣的平均運行時間從0.965秒增大到99.399秒,后者是前者的大約100倍。縱向來比,產生J個樣本的時間比Gibbs/IBF,當J=200時,該比值為30.54;當J=20000時,該比值增大到3058.43。說明要產生相同的樣本量J=20000,Gibbs抽樣的運行時間是IBF算法的運行時間的3058.43倍。可見IBF抽樣比Gibbs抽樣快很多,特別是產生大樣本時。
4 結論
本文提出了估計線性回歸模型中回歸系數變點位置的非迭代抽樣算法(IBF),該算法能夠獲得變點位置的精確后驗分布,進而得到該后驗分布的的獨立同分布的樣本,然后依據該樣本對變點位置做統計推斷。該算法巧妙地避開了Gibbs抽樣等MCMC方法的收斂性診斷問題,所獲樣本為簡單隨機樣本,可直接用來進行統計推斷。模擬顯示該算法能夠有效地估計未知變點位置,并且與迭代的Gibbs抽樣相比,該非迭代抽樣算法的運行時間大大縮短。
[1]Chen J,Gupta A K.Parametric Statistical Change Point Analysis:With Applications to Genetics,Medicine,and Finance(2nd edition)[M].Boston:Birkhauser,2012.
[2]Quandt R E.The Estimation of The Parameters of a Linear Regression System Obeys Two Separate Regimes[J].Journal of the American Statistical Association,1958,(53).
[3]Quandt R E.Tests of the Hypothesis That a Linear Regression System Obeys Two Separate Regimes[J].Journal of the American Statistical Association,1960,(55).
[4]Kim H J,Siegmund D.The Likelihood Ratio Test for a Change-Point in Simple Linear Regression[J].Biometrika,1989,76(3).
[5]Kim H J.Tests for a Change-point in Linear Regression[J].IMS Lecture Notes-Monograph Series,1994,(23).
[6]Ferreira P E.A Bayesian Analysis of a Switching Regression Model:Known Number of Regimes[J].Journal of the American Statistical Association,1975,(70).
[7]Chin Choy J H,Broemeling L D.Some Bayesian Inferences for a Changing Linear Model[J].Technometrics,1980,(22).
[8]Holbert D.A Bayesian Analysis of a Switching Linear Model[J].Journal of Econometrics,1982,(19).
[9]Chen J.Testing for a Change Point in Linear Regression Models[J].Communications in Statistics-Theory and Methods,1998,(27).
[10]Tian G L,Tan M,Ng K W.An Exact Non-iterative Sampling Procedure for Discrete Missing Data Problems[J].Statistica Neerlandica,2007,61(2).
[11]Tian G L,Ng K W,Li K C et al.Non-iterative Sampling-based Bayesian Methods for Identifying Change Points in the Sequence of Cases of Hemolytic Uremic Syndrome[J].Computational Statistics and Data Analysis,2009,53(9).
[12]楊豐凱,袁海靜.正態均值變點識別的非迭代抽樣算法[J].統計與決策,2016,(8).

