自轉旋翼機橫航向穩(wěn)定性分析

王天欣

（西北工業(yè)大學附屬中學 陜西 西安 710000）

1 引言

自轉旋翼機是介于固定翼飛機和直升機之間的一種特殊的機型，它的發(fā)展為直升機后面的崛起奠定了堅實的基礎。自轉旋翼機是第一種直接使用旋翼產(chǎn)生升力的飛機，因此它是直升機的先驅者。自轉旋翼機以無動力旋翼為主要升力面，螺旋槳提供推力或者牽引力，起飛方式主要是滑跑。有些復雜的旋翼機可以實現(xiàn)垂直起降或者超短距起降，因為可以安裝預轉機構或者旋翼槳尖噴氣，自轉旋翼機兼具固定翼飛機和直升機的優(yōu)點，如經(jīng)濟性好、結構簡單、安全性好及振動噪聲小等[1，2]。它在運動和娛樂飛行中越來越流行，但至今沒有發(fā)現(xiàn)它在商業(yè)和軍事中的實際用途，而這和此種飛機的適航性有很大的關系，研究它的穩(wěn)定性對于自轉旋翼機適航性的制定和揭示它的飛行力學本質有著重大的意義。對于自轉旋翼機的研究，國外主要集中在Glasgow大學的Houston教授團隊[3-9]，國內南航的李建波團隊對此也做了大量的工作。著名直升機專家Leshiman教授對自轉旋翼機的技術發(fā)展做了全面的總結，本文研究的對象為西班牙的ELA 07自轉旋翼機，如圖1。

圖1 ELA 07自轉旋翼機

2 旋翼機建模

2.1 部件建模

本文采用部件建模方法，包括機身、旋翼、螺旋槳、尾翼，綜合考慮計算速度和精確度，旋翼誘導速度采用動量理論計算，針對本機型特殊的主旋翼，它的來流是從下至上傳過槳盤，結合它獨特的特性，推導出旋翼氣動模型，其它幾個部件的模型比較簡單，在此不再贅述。

2.2 穩(wěn)定性分析模型

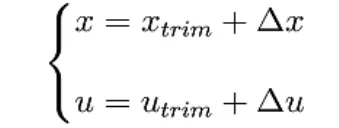
帶入運動方程中即可得到：

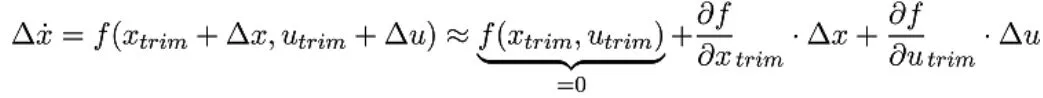
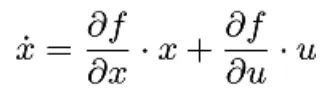
將其表示為狀態(tài)方程形式，令：

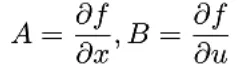
其中A為小擾動線化模型的狀態(tài)矩陣，B為小擾動線化模型的控制矩陣。矩陣A、B的求法有兩種，一種方法是通過數(shù)值方法求解運動微分方程在平衡點處的Jacobian矩陣。這種方法可以快速得到矩陣A、B的近似值而無需進行數(shù)學公式的推導。

3 橫向穩(wěn)定性分析

3.1 橫向模態(tài)求解

運用差分法計算橫向力和力矩對v，p，r，的導數(shù)。所有物理量都是在歐美體軸系定義的，Y是y方向的合力，L為滾轉力矩；為偏航扭矩；v為機體速度在體軸系y方向的分量；p為滾轉角速度；r為偏航角速度；Y為的函數(shù)，且為平衡位置點。

從而可以在復平面畫出自轉旋翼機特征根軌跡，如圖2，箭頭的方向表示速度增大的方向。

圖2 特征根軌跡Fig.2 Identified model eigenvalues

3.2 運動模態(tài)分析

從表2和圖2可以明顯看出，荷蘭滾模態(tài)隨著前飛速度的增加穩(wěn)定性增強，它的特點是對應于橫航向擾動運動特征根的一對共軛復根，為頻率較快、中等阻尼的周期振蕩運動。而螺旋與滾轉的耦合模態(tài)隨著前飛速度的增加穩(wěn)定性減弱，它的特點是低頻，所含的滾轉模態(tài)是衰減很快的單調模態(tài)，其半衰期很短，對應于大負值特征根，主要表現(xiàn)為擾動恢復初期滾轉角速度的迅速衰減變化，而偏航角速度、側滑角等變化很小。螺旋模態(tài)是單調模態(tài)，對應于離原點很近的特征根，不論收斂或發(fā)散都很緩慢，主要表現(xiàn)為擾動運動后期滾轉角（以及偏航角）的變化。

3.3 橫向定量分析

（1）半衰期計算

（2）周期、振蕩頻率、阻尼比計算

4 結語

由于所建立的模型是一種開環(huán)狀態(tài)，所以存在不穩(wěn)定根也是正常的，總體來說，自轉旋翼機的橫航向穩(wěn)定性較好，荷蘭滾模態(tài)在速度較小時不穩(wěn)定，到了40m/s時變得穩(wěn)定，并且隨著速度的增加，穩(wěn)定性逐漸增強，自轉旋翼機高速時穩(wěn)定性較好。滾轉與螺旋的耦合模態(tài)低速時穩(wěn)定，隨著速度增大，穩(wěn)定性減弱，在速度較大時不穩(wěn)定。

[1]頓文強.無人駕駛自轉旋翼機飛行控制技術研究[D].北京航空航天大學，2015.

[2]王煥瑾，高正.自轉旋翼的氣動優(yōu)勢和穩(wěn)定轉速[J].航空學報，2001，22(4):337-339.

[3] Houston S S.Identification of autogyro longitudinal stability and control characteristics[J].Journal of guidance,control, and dynamics,1998，21(3):391-399.

[4] Houston S S.Validation of a rotorcraft mathematical model for autogyro simulation[J].Journal of Aircraft,2000,37(3):403-409.

[5]王俊超，李建波，韓東.自轉旋翼機飛行性能理論建模技術[J].航空學報，2014，12:3244-3253.

[6]王俊超，譚劍鋒，李建波，徐明.基于自由尾跡方法的自轉旋翼氣動特性研究[J].航空學報，2015，11:3540-3548.

[7]王俊超，李建波.機翼對自轉旋翼機縱向穩(wěn)定性的影響[J].航空學報，2014，01:151-160.

[8] Leishman J G.Development of the autogyro:a technical perspective[J].Journal of Aircraft,2004,41(4):765-781.

[9]朱清華.自轉旋翼飛行器總體設計關鍵技術研究[D].南京航空航天大學，2007.