基于區(qū)間重合度的雷達與ESM航跡關聯(lián)算法

(海軍航空工程學院電子信息工程系,山東煙臺264001)

基于區(qū)間重合度的雷達與ESM航跡關聯(lián)算法

關 欣,彭彬彬,衣 曉

(海軍航空工程學院電子信息工程系,山東煙臺264001)

針對時變系統(tǒng)誤差的情況,提出了一種基于區(qū)間重合度的雷達與電子支援措施(ESM)航跡關聯(lián)算法。分析了時變系統(tǒng)誤差對雷達與ESM測量數(shù)據(jù)的影響,將時變系統(tǒng)誤差下航跡的不確定性轉(zhuǎn)化為區(qū)間問題,通過區(qū)間的重合度來衡量雷達與ESM航跡關聯(lián)程度,建立了灰色關聯(lián)分析模型,實現(xiàn)了無需系統(tǒng)誤差配準下的雷達與ESM航跡關聯(lián)。在不同誤差下進行了仿真對比,仿真結果表明,該算法能有效地實現(xiàn)時變系統(tǒng)誤差下的雷達與ESM航跡關聯(lián),具有良好的魯棒性。

航跡關聯(lián);雷達;電子支援措施;系統(tǒng)誤差;區(qū)間重合度

0 引言

在多傳感器信息融合領域,航跡關聯(lián)一直是相當重要且棘手的問題。近年來,由于電子情報系統(tǒng)在軍事領域發(fā)揮著越來越大的作用,異類傳感器的航跡關聯(lián)日益成為國內(nèi)外研究的熱點。作為當前使用最廣泛的兩種傳感器,雷達與ESM的航跡關聯(lián)是典型的異類傳感器航跡關聯(lián)問題[1]。文獻[2-4]研究基于統(tǒng)計理論的雷達與ESM航跡關聯(lián)算法,通常是通過量測構造統(tǒng)計量,然后依據(jù)門限進行關聯(lián)判決。這種方法限制條件少,算法的適用能力較好,但關聯(lián)性能仍需調(diào)高。文獻[5]對統(tǒng)計理論方法進行拓展,提出了基于模糊綜合評判的雷達與ESM航跡關聯(lián)算法,減少了部分計算量。為了更充分地利用雷達與ESM的信息,文獻[6]基于極大似然估計提出了一種直角坐標系下雷達與ESM航跡關聯(lián)方法,并分析了正確和錯誤關聯(lián)概率的表達式,文獻[7]簡化了這一表達式。文獻[8]研究了有偏估計下雷達與ESM航跡關聯(lián)的問題,分析了有偏估計對統(tǒng)計量的影響。由于ESM只有角度信息,為了確保濾波不發(fā)散,要求ESM傳感器相對目標進行一定的機動[9]。文獻[10]在修正極坐標系下構造了不同的關聯(lián)統(tǒng)計量,分析了各種參數(shù)對關聯(lián)方法的影響。文獻[11]在修正極坐標系的前三個狀態(tài)向量的基礎上,增加了兩個新的狀態(tài)量,提高了航跡關聯(lián)性能。但是上述文獻均未考慮系統(tǒng)誤差的影響。

文獻[12]對系統(tǒng)誤差下雷達與ESM航跡關聯(lián)進行了研究,發(fā)現(xiàn)存在系統(tǒng)誤差時,傳統(tǒng)的統(tǒng)計方法構造的統(tǒng)計量不再服從標準的卡方分布,而是服從非中心卡方分布。文獻[13]仍用統(tǒng)計的思路處理系統(tǒng)誤差下雷達與ESM航跡關聯(lián)問題,由于系統(tǒng)誤差是未知的,無法獲知確切門限,并未提出有效的解決方法。上述文獻為分析簡便,將系統(tǒng)誤差描述為恒定不變的常量,而未對時變系統(tǒng)誤差下的情況進行討論[14-15]。本文首先分析了時變系統(tǒng)誤差對雷達與ESM測量數(shù)據(jù)的影響,然后基于灰色系統(tǒng)理論,將時變系統(tǒng)誤差下的不確定性問題,轉(zhuǎn)化為區(qū)間數(shù)的確定問題,避免了統(tǒng)計方法無法確定門限及誤差積累的問題,仿真表明本文方法能有效地解決時變系統(tǒng)誤差下的雷達與ESM航跡關聯(lián)問題。

1 時變系統(tǒng)誤差下雷達與ESM的區(qū)間描述

假設二維情況下,位于同一平臺的雷達與ESM共同對目標進行定位跟蹤,k時刻的位置為(x s(k),y s(k)),目標的位置為(x t(k),y t(k))。雷達在k時刻量測由距離和方位角共同組成,且該量測同時受到時變系統(tǒng)誤差和隨機量測噪聲影響,則

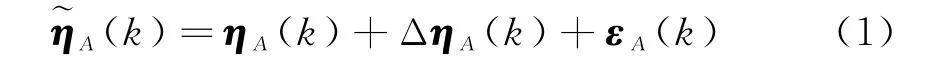
ΔηA(k)雖然是隨時間變化的。但是在實際工程中,傳感器的系統(tǒng)誤差是有范圍的,若超出一定的范圍,則該數(shù)據(jù)是不可信的,不能用于實際當中的。因此,不妨假設雷達允許的最大系統(tǒng)誤差為(本文假設傳感器最大系統(tǒng)誤差大于零),最小系統(tǒng)誤差均為零。

同理,ESM在k時刻的量測

式中,θB(k)為目標相對于ESM的真實方位角,ΔθB(k)為ESM時變的測角系統(tǒng)誤差,ESM測角誤差εB(k)服從具有零均值、恒定方差的高斯分布。不妨假設ESM測角系統(tǒng)誤差最大為最小為零。

對雷達與ESM分別進行跟蹤,濾波效果良好時可忽略隨機誤差,k時刻得到的估計為得到ESM角度估計為由于系統(tǒng)誤差的時變特性,目標的真實位置是無法獲知的。但是當知道系統(tǒng)誤差的變化范圍后,真實目標可能存在的區(qū)域成為不確定區(qū)域,如圖1所示。

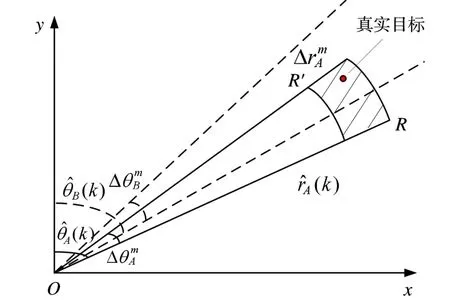
圖1 系統(tǒng)誤差下的不確定區(qū)域

對于雷達目標而言,真實目標不確定區(qū)域是一塊圓環(huán)段區(qū)域,圖中R為雷達目標的估計位置,R′為根據(jù)雷達的最大系統(tǒng)誤差反推得到的最遠的位置,真實目標以極大的概率位于此區(qū)域內(nèi)。對于ESM目標,由于ESM僅有角度信息,只能確定目標位于ESM角度估計和反推的角度之間。可知雖然目標某時刻的具體位置是不確定的,但是目標位置所處的區(qū)間幾乎是確定的,這就將不確定問題轉(zhuǎn)化為確定問題進行分析,接下來對其進行區(qū)間描述。

假設k時刻第i個雷達目標的距離不確定區(qū)間為,其中

i=1,2,…,n A,n A為雷達探測到目標的個數(shù)。由于目標的真實方位范圍可能包含正北方向,即會出現(xiàn)角度值0和2π之間的跳變,所以角度不確定區(qū)間代表從順時針到的區(qū)間,而并不嚴格要求

同理,對于第j個ESM目標角度不確定區(qū)間為,其中

j=1,2,…,n B,n B為ESM探測到目標的個數(shù)。

2 基于區(qū)間重合度雷達與ESM航跡關聯(lián)方法

當雷達目標與ESM目標源于同一個目標時,其真實目標不確定區(qū)域極大概率出現(xiàn)重合。換言之,從統(tǒng)計的角度來講,雷達與ESM真實目標不確定區(qū)域重合度越大,越有可能是源于同一個目標。對于二維情況同地配置的雷達與ESM,由于ESM沒有距離信息與雷達匹配,所以真實目標不確定區(qū)域只考慮角度信息。

一維區(qū)間在實數(shù)范圍內(nèi)存在三種關系:相離、相交和包含。相離表示雷達與ESM真實目標不確定區(qū)域不存在重合,即雷達與ESM目標極大概率來自于不同目標;相交和包含表示雷達與ESM真實目標不確定區(qū)域存在重合,表示雷達與ESM目標可能來自于同一目標,重合度越大,來自于同一目標的可能性越大。令α(I)表示取區(qū)間I的長度,k時刻第i個雷達目標和第j個ESM目標角度不確定區(qū)間的重合度為

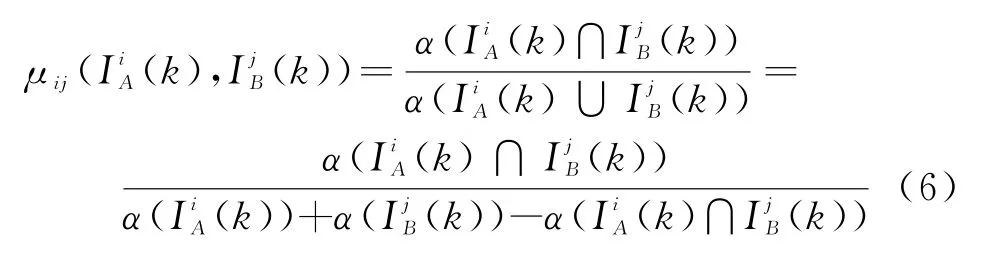
式中,I A∩I B表示區(qū)間I A和區(qū)間I B的交,I A∪I B表示區(qū)間I A和區(qū)間I B的并。

表1 α(I iA(k)∩I jB(k))的表達式

ESM屬于無源傳感器,其探測到的目標對應于輻射源,通常某個平臺(對應雷達目標)上載有若干個輻射源,所以進行雷達與ESM航跡關聯(lián)時,選取ESM的第j個航跡作為已知模式[16],雷達航跡i作為待識別模式,i=1,2,…,n B,文獻[17]給出了灰關聯(lián)四公理,由于本文中來自于同一目標的可能性越大,區(qū)間重合度越大,如果按照傳統(tǒng)方法直接將代入關聯(lián)系數(shù)公式,會導致關聯(lián)系數(shù)不滿足關聯(lián)四公理的接近性。故定義k時刻兩者的關聯(lián)系數(shù)為

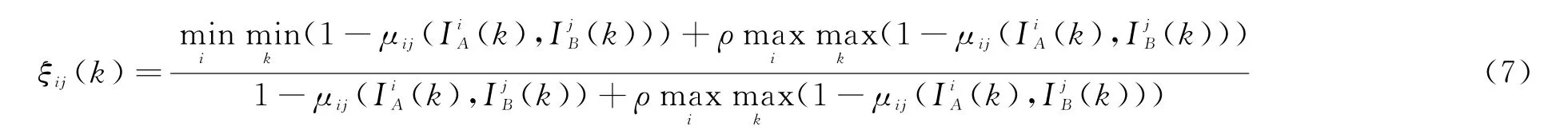
式中,ρ∈[0,1]為分辨系數(shù),一般取0.5。此時,且其值越小,關聯(lián)系數(shù)越大,滿足關聯(lián)四公理。

k時刻ESM航跡j與雷達航跡i的灰關聯(lián)度為

為了對雷達航跡與ESM航跡關聯(lián)進行判決,對關聯(lián)度按遞增排序,采用最大關聯(lián)判別原則,即則判斷k時刻雷達航跡i與ESMj航跡關聯(lián)。

3 仿真分析

為了驗證本文提出關聯(lián)算法的有效性,用本文的算法與傳統(tǒng)統(tǒng)計方法[13]提出的基于角度統(tǒng)計量的算法關聯(lián)性能進行仿真對比實驗。仿真中,正確關聯(lián)概率為Pc=Nc/(Nc+Nm+Nf),錯誤關聯(lián)概率為Pf=Nf/(Nc+Nf+Nm),漏關聯(lián)概率為Pm=Nm/(Nc+Nm+Nf),其中Nc,Nf和Nm依次為實驗中正確、錯誤和漏關聯(lián)的點跡對的數(shù)目,且有Pc+Pf+Pm=1。

假設雷達與ESM位于同一個觀測平臺,平臺初始位置為(0 km,0 km),以π/2的航向和60 m/s的速度勻速直線運動。以(30 km,25 km)與(50 km,45 km)為對角的矩形作為目標存在區(qū)域,隨機產(chǎn)生5個勻速目標,目標的初始速度和初始航向分別在50～70 m/s和0～2π內(nèi)均勻分布[18]。雷達與ESM已實現(xiàn)時間對準且采樣時間均為1 s,允許的漏關聯(lián)概率為0.1,雷達測距的隨機誤差和最大系統(tǒng)誤差均為100 m。

3.1 不同系統(tǒng)誤差對算法的影響

條件設置如表2所示,在上述條件下各進行100次蒙特卡洛仿真,選取正確和漏關聯(lián)概率作為比較指標,結果如圖2和圖3所示。

表2 不同系統(tǒng)誤差設置表

圖3為實驗3條件下雷達與ESM關于某個目標的角度估計,在傳統(tǒng)以高斯噪聲或者時不變系統(tǒng)誤差為基礎的文獻[10-13]中,目標的角度估計往往較平滑,而時變系統(tǒng)誤差下,角度估計與真實狀態(tài)存在嚴重偏差,且偏差隨著時間變化,這為雷達與ESM航跡關聯(lián)增加了難度。

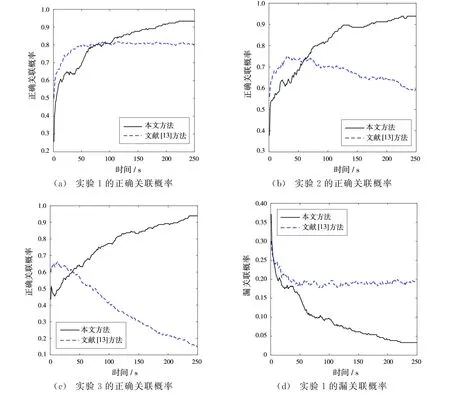
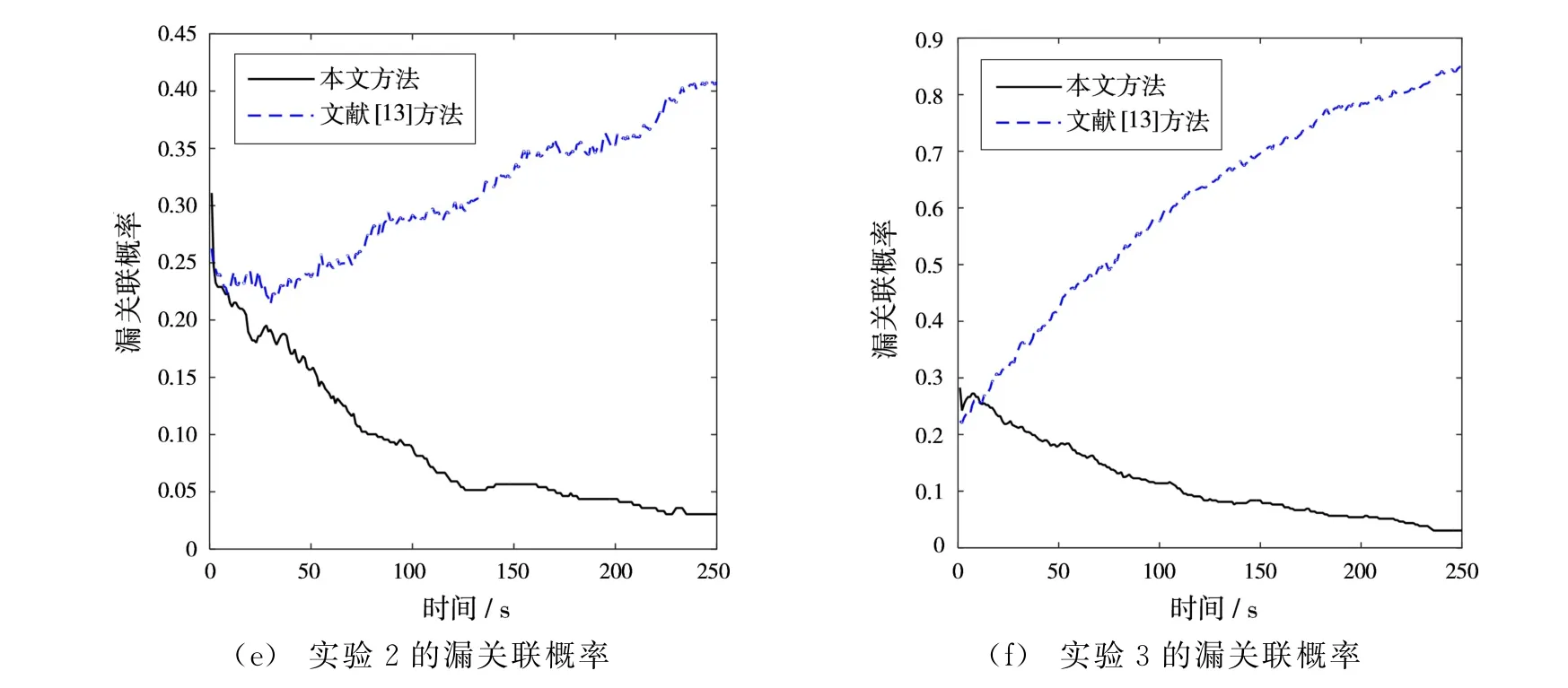
圖2 不同系統(tǒng)誤差下雷達與ESM航跡關聯(lián)概率

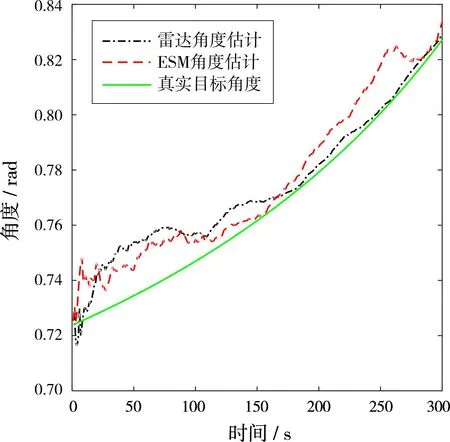
圖3 雷達與ESM關于目標的角度估計

從圖2(a)中可以看出,文獻[13]方法在系統(tǒng)誤差較小時,誤差隨時間累積的效果不明顯,仍表現(xiàn)出較好的關聯(lián)性能;但是隨著系統(tǒng)誤差的增大,漏關聯(lián)概率增加,正確關聯(lián)概率曲線是先升后降的,即隨著時間推進,更多的樣本數(shù)不僅沒有增加有用信息,反而導致誤差累積,說明傳統(tǒng)的統(tǒng)計方法不適用于處理時變系統(tǒng)誤差下雷達與ESM航跡關聯(lián)問題。從圖2可以看出,不同系統(tǒng)誤差下,本文所提方法能保持較高的正確關聯(lián)概率,漏關聯(lián)概率始終低于文獻[13]方法,具有良好的魯棒性。

3.2 不同隨機誤差對算法的影響

條件設置如表3所示,在上述條件下各進行100次蒙特卡洛仿真,選取正確和漏關聯(lián)概率作為比較指標,結果如圖4所示。

表3 不同隨機誤差設置表

圖4 不同隨機誤差下雷達與ESM航跡關聯(lián)概率

從圖4可以看出,文獻[13]方法隨著雷達與ESM的隨機誤差增大,正確關聯(lián)概率也增大,這是因為統(tǒng)計的方法無法獲得存在系統(tǒng)誤差下的確切門限,導致判決門限與關聯(lián)統(tǒng)計量不相符造成的。當系統(tǒng)誤差的最大值大于隨機誤差時,圖4(a)表明本文方法具有較高的正確關聯(lián)概率;隨著隨機誤差的增大,濾波效果下降,可能導致真實目標不位于式(4)和式(5)中的目標不確定區(qū)域,從而導致關聯(lián)性能略微下降,但是正確關聯(lián)概率仍高于80%,優(yōu)于文獻[13]方法。

4 結束語

本文研究了時變系統(tǒng)誤差下的雷達與ESM航跡關聯(lián)問題,提出了一種基于區(qū)間重合度的雷達與ESM航跡灰色關聯(lián)算法。將航跡的不確定性轉(zhuǎn)化為區(qū)間問題,通過區(qū)間的重合度來衡量雷達與ESM航跡關聯(lián)程度,并建立了灰色關聯(lián)分析模型。用本文方法與傳統(tǒng)的統(tǒng)計方法[13]進行仿真對比,仿真結果表明,隨著系統(tǒng)誤差的增大,文獻[13]方法漏關聯(lián)概率迅速增大,正確關聯(lián)迅速減小,而本文方法始終維持較高的關聯(lián)性能,表現(xiàn)出良好的魯棒性;文獻[13]由于判決門限與關聯(lián)統(tǒng)計量不相符,出現(xiàn)了隨著隨機誤差增大,正確關聯(lián)概率增大的反常現(xiàn)象,本文方法關聯(lián)性能略微下降,仍具有80%以上的正確關聯(lián)概率,表明了本文方法的有效性。

[1]何友,王國宏,關欣,等.信息融合理論及應用[M].北京:電子工業(yè)出版社,2010:124-146.

[2]趙宗貴,刁聯(lián)旺,李君靈,等.信息融合工程實踐—技術與方法[M].北京:國防工業(yè)出版社,2014:50-75.

[3]WANG G H,MAO S Y,HE Y.Triple-Threshold Radar to ESM Correlation Algorithm When Each Radar Track Is Specified by Different Number of Meas-urements[J].IEE Proceedings-Radar,Sonar and Navigation,2000,147(4):177-187.

[4]CHEN H,BAR-SHALOM Y.Track Association and Fusion with Heterogeneous Local Trackers[C]∥46th IEEE Conference on Decision and Control,2007:2675-2680.

[5]王國宏,何友.基于模糊綜合和統(tǒng)計假設檢驗的雷達與ESM相關方法[J].系統(tǒng)工程與電子技術,1997(4):13-16.

[6]FARINA A,MIGLIOLI R.Association of Active and Passive Tracks for Airborne Sensors[J].Signal Processing,1998,69(3):209-217.

[7]WANG G H,MAO S Y,HE Y.Analytical Performance Evaluation of Association of Active and Passive Tracks for Airborne Sensors[J].Signal Processing,2003,83(5):973-981.

[8]WANG G H,ZHANG X Y,TAN S C.Effect of Biased Estimation on Radar-to-ESM Track Association[J].Journal of System Engineering and Electronic Techniques,2012,23(2):188-194.

[9]王國宏.利用角度、角度變化率和ITG信息的主被動傳感器數(shù)據(jù)關聯(lián)[J].雷達科學與技術,2003,1(1):39-45.WANG Guohong.Heterogeneous Sensor Data Association by Using Angle,Angle Rate and ITG Information[J].Radar Science and Technology,2003,1(1):39-45.(in Chinese)

[10]SCALA B F L,FARINA A.Choosing a Track Association Method[J].Information Fusion,2002,3(2):119-133.

[11]ZHOU Y F,LI W,LEUNG H.Maximum Likelihood Based ESM/Radar Track Association Algorithm in a New Modified Polar Coordinate[R].Ottawa:Defence Research and Development Canada,2004.

[12]張翔宇,王國宏,李世忠.系統(tǒng)誤差對雷達與ESM航跡關聯(lián)的影響[J].火力與指揮控制,2011,36(7):39-41.

[13]宋振宇,張翔宇,張光軼.系統(tǒng)誤差對異地配置的雷達和ESM航跡關聯(lián)的影響[J].電光與控制,2014,21(3):42-46.

[14]ZHANG F,ALOIS K.Systematic Error Modeling and Bias Estimation[J].Sensors,2016,16(5):729-829.

[15]衣曉,張懷巍,曹昕瑩,等.基于區(qū)間灰數(shù)的分布式多目標航跡關聯(lián)算法[J].航空學報,2013,34(2):352-360.

[16]衣曉,關欣,何友.分布式多目標跟蹤系統(tǒng)的灰色航跡關聯(lián)模型[J].信號處理,2005,21(6):653-655.

[17]劉思峰,黨耀國.灰色系統(tǒng)理論及其應用[M].北京:科學出版社,2010.

[18]龍海鷹,任清安.空管異類傳感器數(shù)據(jù)融合算法研究[J].雷達科學與技術,2010,8(6):526-531.LONG Haiying,REN Qingan.Research on Data Fusion Algorithm of ATC Heterogeneous Sensors[J].Radar Science and Technology,2010,8(6):526-531.(in Chinese)

Track Association Algorithm of Radar and ESM Based on the Interval Overlap Ratio

GUAN Xin,PENG Binbin,YI Xiao
(Department of Electronic and Information Engineering,Naval Aeronautical and Astronautical University,Yantai264001,China)

Aiming at the situation with time-varied systematic errors,a gray track association algorithm of radar and ESM based on interval overlap ratio is proposed in this paper.The effect of time-varied systematic errors on the measurements of radar and ESM is analyzed and the uncertainty of tracks is turned into an interval problem in the presence of time-varied systematic errors.The correlation is measured by the interval overlap ratio and a gray model is established,which realize the track association of radar and ESM without registration.Simulation is carried out with different errors,and the results show that the proposed method can achieve the track association of radar and ESM effectively and has good robustness.

track association;radar;electronic support measures(ESM);systematic errors;interval overlap ratio

TN957

A

1672-2337(2017)01-0061-07

10.3969/j.issn.1672-2337.2017.01.011

2016-08-11;

2016-09-27

國家自然科學基金(No.61032001);教育部新世紀優(yōu)秀人才支持計劃(No.NCET-11-0872)

關欣女,1978年生,遼寧錦州人,教授、博士生導師,主要研究方向為多源信息融合、智能信息處理。

彭彬彬男,1991年生,安徽安慶人,碩士,主要研究方向為異類傳感器航跡關聯(lián)。E-mail:913140043@qq.com

衣曉男,1977年生,山東棲霞人,教授、博士生導師,主要研究方向為無線傳感器網(wǎng)絡、多源信息融合。per.edu.cn/html/releasepaper/2009/09/33.