靜電場電位邊值問題唯一性定理的補充與完整證明

陳文卿 閆 述

(江蘇大學計算機科學與通信工程學院，江蘇 鎮江 212013)

靜電場電位邊值問題唯一性定理的補充與完整證明

陳文卿 閆 述

(江蘇大學計算機科學與通信工程學院，江蘇 鎮江 212013)

本文對靜電場電位邊值問題與解的唯一性定理作了補充與完整的證明．首先將區域邊界與銜接邊界從通常的混稱中區分開來，確認了靜電場邊值問題中第三類邊界條件應有的形式，在解的唯一性定理中增加了銜接條件和無限遠邊界條件，并根據數學表達式的形式重新歸類。然后在區域邊界條件、無限遠邊界條件和銜接條件下電位解的唯一性的證明中，討論了第一、第三類邊值問題電位解的唯一性與全二類邊界條件下電位存在常數差的問題，解除了第三類邊界條件系數為正的限制，說明了整個求解空間為無限大時適用的邊值問題。最后通過例題說明了區域、無限遠和銜接3種邊界條件在解題中的應用。補充后的定理可以更好地作為解題和后續學習的依據和基礎。

電位的邊值問題；區域邊界條件；銜接條件；唯一性定理；證明

電位的邊值問題與解的唯一性是通信和電子信息類相關專業本科階段電磁場與電磁波和電動力學課程中靜電場部分的重要內容，也是求解其他邊值問題的基礎。該課程的現行教材中，普遍證明了第一、第二類邊界條件[1-19]，對第三類邊界條件的定義大多與《數學物理方法》[20,21]中的定義不同[1-11]，有的相同[12-15]。當求解區域不止包含一種媒質或無限大時，也需要將銜接條件[15-17,20-22]和無限遠邊界條件[11-15,22]均納入唯一性定理[15]，并給出完整的證明。為此，本文定義與區分了區域邊界條件與銜接邊界條件，確認了第三類邊界條件應有的形式，將無限遠邊界和銜接條件均納入唯一性定理，并根據Helmholtz定理說明了無限遠邊界條件針對的是Possion方程。在定理的證明中，我們無需規定第三類邊界條件的系數為正[21,22]；將無限遠邊界條件作為齊次第一、第二類條件處理；證明了第一、第三類邊值問題和銜接條件下電位的唯一性，說明了第二類邊值問題電位的解存在常數差的情況；根據銜接條件的數學表達式，將介質與導體的銜接條件歸入第一、第二類邊界條件，在現有工作[23,24]的基礎上，使求解電位邊值問題所依據的唯一性定理的證明更為完備。最后，通過典型的分離變量法例題，說明了區域邊界條件、無限遠邊界條件和銜接條件在解題中的應用。

1 兩種邊界與兩類邊界條件

在靜電(以及更廣泛的電磁)問題中，所要求解區域的邊界稱為區域邊界；如果在此區域中存在一種以上的媒質，不同媒質的分界面稱為銜接邊界[13,20-22](圖1)。區域和銜接邊界上場量所滿足的條件往往通稱為邊界條件[1-12]。為明確起見，建議分別稱為邊界條件和銜接條件。

當求解區域包括場源，均勻、線性、各向同性媒質中電位滿足的Poisson方程為

2Φr=-

(1)

當上述求解區域中無源，電位滿足Laplace方程

2Φr=0

(2)

在區域邊界上，常有3種類型的邊界條件。第一類邊界條件又稱為Dirichlet條件：給定區域邊界上的電位值，

ΦS=f1S

(3a)

第二類邊界條件又稱為Neumann條件：給定區域邊界上電位的法向導數值,

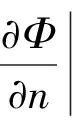
(3b)

第三類邊界條件又稱為Robin條件[16,17]：給定區域邊界上的電位值和電位法向導數的線性組合,

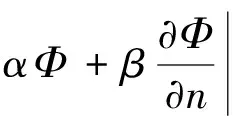
(3c)

式中，α和β均為不為零的實數。第一、第二類邊值問題是第三類邊值問題α和β分別等于零時的特例。第三類邊界條件指的是給定區域邊界上每一點的電位值和電位的法向導數值之和，并不是如式(4)所示那樣在區域的一部分邊界上給定電位值，在另外一部分邊界上給定電位的法向導數值[1-11]。

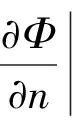
(4)

如果求解區域為整個無限空間，有無限遠處的邊界條件為

式中，R是場點到源點的距離。

當求解區域是分區均勻的，即存在多種媒質(如圖1所示)的情況下，在不同媒質的分界面上，Poisson或Laplace方程不再成立，界面兩邊的場量由銜接條件聯系

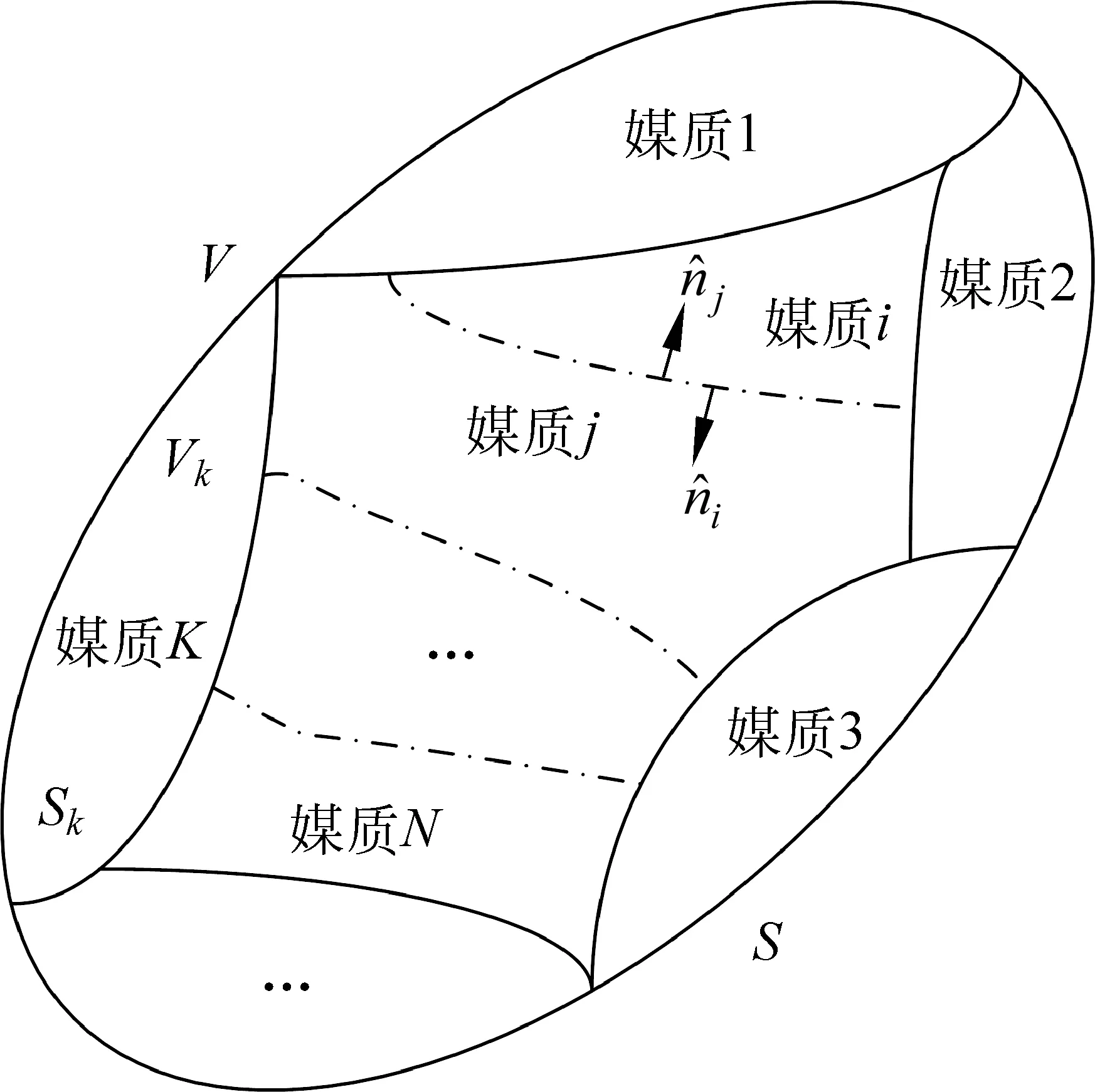
圖1 區域邊界與銜接邊界

式中i≠j，代表媒質i與媒質j；ρS為分界面上的自由電荷面密度。

在介質分界面上沒有自由電荷，銜接條件(6)中的ρS=0，有

在導體與介質的分界面上，由于導體表面為等位面，導體表面上存在感應的自由電荷，故銜接條件式(6)變為

式中C為常數。

區域邊界和銜接邊界可以重合、部分重合或完全不重合。銜接條件(8a)和(8b)分別與第一、第二類邊界條件具有相同的數學形式，故可按區域邊界條件處理。

當求解區域中存在一種以上的媒質時，應在各媒質中分別列出Poisson或Laplace方程，定解條件除給出邊界條件外還要給出銜接條件。

2 完整的電位邊值問題解的唯一性定理與證明

2.1 完整電位邊值問題解的唯一性定理

增加銜接條件和無限遠處的邊界條件后，靜電場電位邊值問題解的唯一性定理可以補充為：在封閉面包圍的介質分區均勻的區域中，當邊界上給定上述第一、第二、第三類邊界條件中的一種(在邊界的不同部分邊界條件的類型可以不同[20,21])，那么區域內的電位由Possion方程或Laplace方程及銜接條件唯一確定。

當求解區域為整個無限空間、源分布在有限區域中時，唯一性定理仍然成立。

對補充后的靜電場電位邊值問題解的唯一性定理分兩步證明，第一步：當求解空間中只有一種媒質時，證明區域邊界條件下解的唯一性；第二步：當求解空間中有一種以上媒質時，證明區域邊界及銜接條件下解的唯一性。

2.2 區域邊界條件和無限遠邊界條件的證明

用反證法。假設在場域中電位φ滿足Poisson方程或Laplace方程，邊界滿足三類邊界條件之一的電位不是唯一的，至少有兩個解，分別記為Φ′和Φ″，令

δΦ=Φ′-Φ″

(9)

將Φ′和Φ″代入Poisson方程(1)和Laplace方程(2)，有

將式(10a)中的兩式和式(10b)中的兩式分別相減后，得到

2δΦ=2Φ′-2Φ″=2Φ′-Φ″=0

(11)

利用第一標量Green公式

(12a)

取式(12a)中兩個標量Ψ和Φ相同等于δΦ，則

(12b)

將式(11)代入上式(12b)，得

(13)

當給定第一類邊界條件

Φ′S=Φ″S=f1(S)

(14a)

那么在邊界S上

δΦS=Φ′S-Φ″S=0

(14b)

故公式(13)

(15)

當給定第二類邊界條件

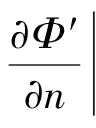
(16a)

那么在域邊界S上

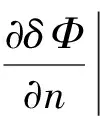
(16b)

故公式(13)

(17)

由式(15)和式(17)可見，對于第一和第二類邊界條件，均有

(18)

式中體積分的被積函數大于或等于零，要使等式成立，被積函數必須為零，即

δΦ=0

(19)

上式表明，電位差δΦ是一個常數，由式(9)可知

δΦ=Φ′-Φ″=C

(20)

由給定的第一類邊界條件式(14)，可知上式中的常數C=0，由于式(9)表示的是V內和S面上所有的Φ′和Φ″，所以邊界面上電位給定時有

Φ′=Φ″

此時電位被唯一確定。

由給定的第二類邊界條件式(16)可知，電位Φ的兩個不同的解相差一個常數

Φ′=Φ″+C

正如對式(20)分析那樣，只要邊界的某一部分存在第一類邊界條件，那么上式中的C=0，電位被唯一確定。如果全部邊界都是第二類邊界條件，那么電位的兩個解相差一個常數，解是不唯一的。鑒于電場強度與電位的梯度關系E=-Φ，故通過電位得到的電場強度E還是唯一的。

第三類邊界條件的證明稍顯復雜。式(3c)中，α和β有同號和異號兩種情況。如果同為正號，式(3c)保持不變；如果同為負號，可將負號歸于等式右邊的函數f3(S)。即當α和β同號時，總可以使α和β為正數，那么當給定第三類邊界條件時

將上面兩式相減后，將式(8)代入

則有

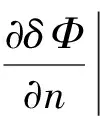
(21)

將式(21)代入式(13)，有

(22)

當α和β異號，假設α為負，那么式(3c)有

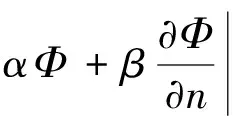
使系數仍為正數。這種情況下，式(12)和式(13)中，在包圍體積V的邊界面S上，相應地

(23)

此時，給定的第三類邊界條件為

將上面兩式相減，并將式(9)代入后，得

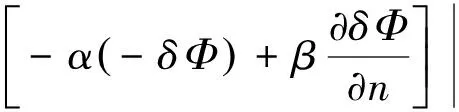
(24a)

那么有

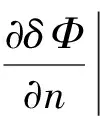
(24b)

將式(24b)代入式(23)，得

(25)

類似地，當設β為負時，也可得到與式(25)同樣的結果。

總之，由于式(22)和式(25)兩邊的被積函數均大于或等于零，面積分的系數均為負，若要使等式成立，等式兩邊必都等于零。所以對于第三類邊界條件，有

與前面第一類邊界條件證明中所做的分析相同，在邊界上滿足第三類邊界條件時，電位Φ是唯一的。

綜上所述，場域中電位Φ滿足Poisson方程或Laplace方程，在邊界上滿足第一、第三類邊界條件之一時，電位Φ是唯一的，并且只要在邊界的某一部分存在第一或第三類邊界條件的一種，電位就可以唯一確定。如果全部邊界均為第二類邊界條件時，電位Φ存在常數差解不唯一，但由此得到的電場強度是唯一的。

對于無限遠邊界，公式(5)意味著源分布在有限區域里，遠處的電位及其徑向偏導數

2.3 銜接邊界條件的證明

在圖1中，在S包圍的區域V內第K個媒質構成的均勻分區Vk中Possion方程(1)和Laplace方程(2)為

仍然用反證法證明。設有兩組不同的解Φ′和Φ″同時滿足唯一性定理的條件，類似式(8)有

(28)

同樣地，將Φ′和Φ″在代入Poisson方程(27a)和Laplace方程(27b)后，有

將式(29a)中的兩式和式(29b)中的兩式分別相減后

(30)

將Ψ=δΦk和Φ=εkδΦk代入第一標量Green公式(11a)中，有

(31a)

將式(30)代入式(31a)后

(31b)

若V內共有N個均勻分區，將會得到N個如式(31b)的方程，累加后有

(32)

式中，包圍Vk的Sk可被分解成界面S的一部分，和(或者)相鄰分區界面的共同部分。設構成界面S的共有L片，構成相鄰界面共同部分的共有M片，故上式的面積分可寫為

(33a)

上式的第二項面積分中，相鄰界面Si與Sj的法向方向相反，且在界面Si與Sj兩邊有銜接條件(6)，式(33a)中

(33b)

將式(33b)代入式(32)后，有

(34)

在2.2中，已經證明上式(34)等號右邊滿足區域邊界條件(3)的面積分為零，有

由于被積函數必定大于或者等于零，若要積分成立，必有

δΦk=0

類似地，上式表明δΦk是一個常數，由式(28)有

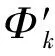
由銜接條件式(7a)和式(8a)可知，上式中的C=0，由此銜接條件得證。

3 分離變量法的解題實例

現以教材中常常出現的分離變量法例題，說明唯一性定理中補充的無限遠邊界條件和銜接條件的作用。

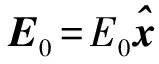
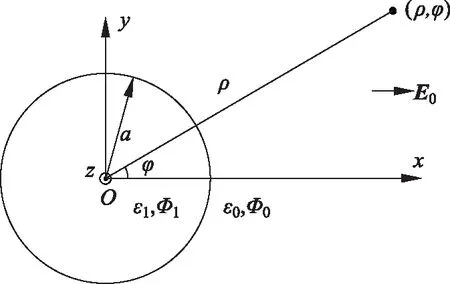
圖2 均勻電場中的介質圓柱

解： 根據界面形狀選取圓柱坐標系，且使z軸與介質柱軸重合。根據已知條件，電場和介質柱在z方向是均勻的，求解區域內無自由電荷分布，電位只是ρ、φ的函數，滿足二維Laplace方程。在ρOφ平面上，介質柱面上的束縛電荷為環形有限分布，根據無限遠邊界條件式(5)，在ρ→∞處，介質圓柱對電位的影響可以忽略。至于外加均勻電場的電位，宜選取柱心電位為參考點，設Φx=0=0則無限遠處的電位

化為圓柱坐標后

Φ∞=-E0ρcosφ

在真空和介質柱交界處，Laplace方程不成立。設介質柱外為區域0，電位為Φ0，柱內為區域1，電位為Φ1，需在這兩個區域中分別列出Laplace方程

介質柱與真空的分界面上無自由電荷，上式中的待求量Φ0和Φ1通過銜接條件(6)

相聯系。

隨后通解形式的確定，待定系數的確定和解的線性組合，按通常的步驟進行。

4 結論

靜電場電位邊值問題解的唯一性定理在解題過程中起著指導作用。明確各類邊界條件的定義，補增銜接條件和無限遠邊界條件，得到完整的定理可以規范解題過程，使解題依據更加充分。電位的邊界問題本質是偏微分方程的邊值問題，定理的補充和完整證明更便于后續學習其他位函數的邊值問題如恒定電流場的電位，無源區恒定磁場的磁位等問題。在無限遠邊界的補充和證明中，僅處理了整個的無限大空間，場域無限大時，無限遠處的電位一般為零，這與電荷分布在有限區域中一般選取無限遠作為參考點一致，對于場域存在局部無限大條件時無限大處電位的確定有待進一步考慮。

對于從實際中抽象出的位函數的邊值問題，大多數的解都是存在的，本文在此前提下證明了解的唯一性。但是，所設邊界條件還應符合物理的、數學的規律，否則可能無解[25]。

[1] 畢德顯. 電磁場理論[M]. 北京: 電子工業出版社, 1985.

[2] 林為干, 符果行, 鄔琳若，等. 電磁場理論: 修訂本[M]. 北京: 人民郵電出版社, 1996.

[3] 楊顯清. 電磁場與電磁波[M]. 北京: 國防工業出版社, 2003.

[4] 謝處方, 饒克謹. 電磁場與電磁波[M]. 北京: 高等教育出版社, 2006.

[5] Cheng, David K. Field and wave electromagnetics[M]. Peking: Tsinghua University Press, 2007.

[6] 楊儒貴. 電磁場與電磁波[M]. 北京: 高等教育出版社, 2007.

[7] 焦其祥. 電磁場與電磁波[M]. 北京: 科學出版社, 2010.

[8] 路宏敏, 趙永久, 朱滿座. 電磁場與電磁波基礎[M]. 北京: 科學出版社, 2012.

[9] 張洪欣, 沈遠茂, 韓宇南. 電磁場與電磁波[M]. 北京: 清華大學出版社, 2013.

[10] 鄒澎, 周曉萍. 電磁場與電磁波[M]. 北京: 清華大學出版社, 2016.

[11] 符果行. 電磁場與電磁波基礎教程[M]. 北京: 電子工業出版社, 2016.

[12] 倪光正. 工程電磁場原理[M]. 北京: 高等教育出版社, 2009.

[13] 郭輝萍, 劉學觀. 電磁場與電磁波[M]. 西安: 西安電子科技大學出版社, 2015.

[14] 雷銀照. 電磁場[M]. 北京: 高等教育出版社, 2008.

[15] 馮慈璋, 馬西奎. 工程電磁場導論[M]. 北京: 高等教育出版社, 2000.

[16] 郭碩鴻. 電動力學[M]. 北京: 高等教育出版社, 2008.

[17] 羅春榮, 陸建隆. 電動力學[M]. 北京: 西安交通大學出版社, 2000.

[18] 尹真. 電動力學[M]. 北京: 科學出版社, 2005.

[19] 羅春榮, 丁昌林, 段利兵. 電動力學[M]. 北京: 電子工業出版社, 2016.

[20] 梁昆淼. 數學物理方法[M]. 北京: 高等教育出版社, 2010.

[21] 郭敦仁. 數學物理方法[M]. 北京: 高等教育出版社, 1991.

[22] 張渭濱. 數學物理方程[M]. 北京: 清華大學出版社, 2007.

[23] 張秋光. 場論(上冊)[M]. 北京: 地質出版社, 1983.

[24] 林建. 恒定電流場的地下3D目標識別及成像技術研究[D]. 江蘇大學, 2010.

[25] 張秋光. 場論(下冊)[M]. 北京: 地質出版社, 1988.

SUPPLEMENTANDCOMPLETEPROOFOFTHEELECTROSTATICBOUNDARYVALUEPROBLEMANDTHEUNIQUENESSOFSOLUTIONS

CHENWenqingYANShu

(School of Computer Science and Communication Engineering, Jiangsu University, Zhenjiang Jiangsu 212013)

The electrostatic boundary value problem and the uniqueness of solutions are supplemented and proved in this paper. At first, the region condition and the convergence boundary are distinguished from the usual mixed singularity. The form of Robin Problem in electrostatic field boundary value problem is confirmed. The convergence condition and the infinite boundary condition are added to the uniqueness theorem of solutions. These boundary conditions are re-classified according to the form of mathematical expressions. Then in the proof of the uniqueness of the potential solutions under boundary conditions, infinite boundary conditions and convergence conditions, the problem of the coefficient of the third kind of boundary condition and the applicative boundary value problem with infinite space are solved. We also demonstrate the uniqueness of potential solutions for Dirichlet and Robin Problem and constant differences in the potential of Neumann Problem. Finally, the application of region, infinity and convergence boundary conditions in problems solving is illustrated by an example. The supplemented theorem can be better used as the basis for solving problems and follow-up learning.

the boundary value problem of potential; regional boundary condition; convergence condition; uniqueness theorem; proof

2017-05-10；

2017-08-31

國家自然科學基金三維CSAMT響應的時域數值模擬方法(41374129)。

陳文卿，碩士研究生，主要研究方向為電磁場理論和計算，chenwq1102@163.com； 閆述，女，教授，主要從事電磁場的教學和科研工作，研究方向為電磁場理論和計算電磁學，yanshu@ujs.edu.cn。

陳文卿，閆述. 靜電場電位邊值問題唯一性定理的補充與完整證明[J]. 物理與工程，2017，27(6)：54-59.

■