基于能量靈敏度矩陣和多閾值搜索的電壓控制分區

， ，(.中國電力工程顧問集團西南電力設計院有限公司，四川 成都 600；.國網四川省電力公司物資分公司，四川 成都 6005；.四川大學電氣信息學院，四川 成都 60065)

基于能量靈敏度矩陣和多閾值搜索的電壓控制分區

鄭武1，康勇2，李華強3
(1.中國電力工程顧問集團西南電力設計院有限公司，四川 成都 610021；2.國網四川省電力公司物資分公司，四川 成都 610052；3.四川大學電氣信息學院，四川 成都 610065)

目前，能量函數的方法用于電壓穩定評估、電網可靠性分析已獲得較為深入的研究。由于節點的能量信息能綜合反映節點的無功注入以及電壓水平，提出一種基于靜態能量函數法和多閾值搜索進行電壓控制分區的新方法。從節點的能量信息出發，提出節點能量相關度指標用于量化節點間無功聯系的緊密程度，并基于此構建系統的能量靈敏度矩陣，最后利用多閾值分解方法對該矩陣進行電壓控制區域劃分。IEEE 30節點系統、118節點系統的仿真結果以及和傳統分區方法的比較驗證了所提方法的有效性和可行性。

靜態能量函數；能量信息；節點能量相關度指標；能量靈敏度矩陣；多閾值分解

0 引 言

無功電壓控制是電網安全控制的重要組成部分，對確保系統安全、穩定和經濟運行具有重要意義[1-2]。

由于無功傳輸的本地特性，系統內電壓分布呈現明顯的區域特點[3-4]，為保證各區域內電壓運行在合理范圍，充分發揮無功電源的控制作用，提高系統運行的安全性和經濟性，將系統劃分為多個相互解耦的無功電壓控制區域已成為一個重要問題。

迄今為止，國內外學者對電壓控制分區做了一定的研究，已經取得的研究成果主要包括：基于啟發式方法的Tabu搜索法[5-6]，以分區中的節點數以及線路作為目標函數，以分區中的變壓器、電容器數量作為約束條件進行優化，但該方法未考慮網絡的物理特征且在系統較大時其計算量比較大。為減少大系統的優化分區計算量，文獻[7]提出基于遺傳算法的兩層搜索方法用于無功分區控制并取得了較好的效果。文獻[8-10]利用圖論的基本理論，提出閾值和多閾值分解法研究電壓分區，該類方法可直接依據靈敏度矩陣來分析，簡單直接，且具有實際意義[11]。文獻[12-13]提出利用聚類算法研究電壓控制分區，該方法將負荷節點映射到發電機節點組成的空間中，并基于此類空間數據對象的坐標定義電氣距離，但映射后節點坐標的物理意義并不清晰。

以上方法為進一步研究電力系統的電壓控制分區提供了極其重要的借鑒作用。由于節點能量狀態能反映節點的無功注入及電壓水平[13],基于靜態能量函數法，這里提出節點能量相關度指標(node energy correlation degree)量化節點間無功聯系的緊密程度，并定義一個能夠反映系統節點間無功、電壓聯系疏密程度的能量靈敏度矩陣(energy sensitivity matrix)，最后利用多閾值分解方法對該能量靈敏度矩陣進行電壓控制區域(voltage control area,VCA)劃分。所提方法和思路的有效性和可行性在IEEE 30、IEEE 118母線系統的仿真結果中得到了驗證。

1 靜態能量函數法和能量靈敏度矩陣

1.1 靜態能量函數的數學模型

根據線路功率輸送關系，多母線中各節點功率平衡等式[11]為

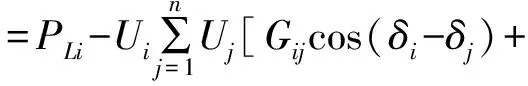
Bijsin(δi-δj)]

(1)

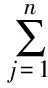
Bijcos(δi-δj))]

(2)

式中:PLi為節點i的注入有功；QLi為節點i的注入無功；Gij為節點i、j之間的電導；Bij為節點i、j之間的電納；δi、δj分別是節點i、j的電壓相角。

靜態能量函數表達式為[13]

(3)

對于具體的某個節點i，基于功率平衡的靜態能量函數表達式為

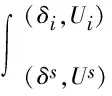
(4)

式中，fi(δi,Ui)、gi(δi,Ui)分別為節點i的有功功率及無功功率平衡表達式。

將式(1)、式(2)代入式(4)，可得多母線系統中第i節點的靜態能量函數Ei的表達式為

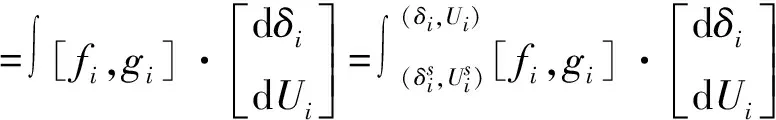
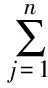
(5)

式中：(Ui,δi)為當前運行情況下各個負荷節點電壓值；(Uis,δis)為系統處于穩定運行點的電壓值。若代入臨界參數值，則Ei表示節點臨界能量。

如果考慮并聯電容器補償，式(5)修改為

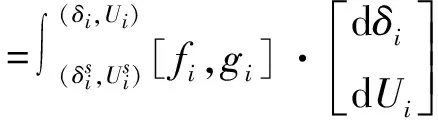
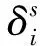
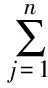
(6)

1.2 能量靈敏度指標構建

依據式(5)、式(6)，無功注入集合Q、電壓U與能量E之間存在如圖1的聯系[13]。

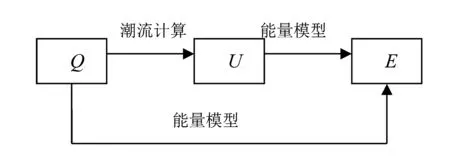
圖1 無功注入集合、電壓與能量之間的聯系

利用靜態能量函數法，式(5)可得到各負荷節點在穩定運行點時的能量值Ei及臨界條件下的能量值Eci。隨著負荷的持續增長，電壓呈不斷下降的趨勢，穩態能量值亦逼近其極限能量值Eci[14]。由圖1，節點電壓通過能量模型影響節點的能量值，同時節點的無功注入作為變量直接影響該節點的能量值。節點能量與電壓以及無功注入之間的相互關系表征了該節點電壓隨能量變化的趨勢。由能量函數模型確定的節點能量狀態與節點的無功、電壓水平密切相關，節點能量值能綜合體現該節點的無功及電壓狀態。

文獻[14]提出節點能量靈敏度指標表示節點電壓隨能量的變化趨勢，并由該節點的能量/電壓趨勢指標判定系統的電壓弱節點，該能量靈敏度指標重在表征節點電壓Ui變化對節點i能量值Ei的影響。

為進一步研究鄰近節點電壓Uj波動對節點i能量值的影響，提出節點能量相關度指標τij來表示鄰近節點間電壓變化對本節點能量的影響：

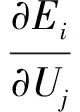
(7)

由于能量值Ei綜合反映了該節點的電壓和無功注入水平，τij的大小表征了不同節點電壓的變化對本節點能量值的影響，因此τij的大小能夠指示相鄰節點與本節點無功相關的緊密程度，亦即無功電壓耦合程度。

1.3 能量靈敏度矩陣

由于節點的能量狀態綜合反映了該節點的無功以及電壓水平，基于這一思想，構建一個與無功/電壓水平緊密相關的能量靈敏度矩陣，并基于此靈敏度矩陣進行VCA劃分。

利用文獻[14]構建的能量靈敏度指標及式(7)構建能量靈敏度矩陣D：

(8)

D是一個n×n矩陣(n為系統節點數)，其實質是以能量對電壓靈敏度的形式反映了系統電壓和無功的動態特性，該矩陣能分辨各相鄰負荷點電壓擾動對系統其他節點無功影響的差異。基于這一差異的大小，可將系統劃分為若干解耦的區域。

D內各元素τij反映的是節點i的電壓波動對節點j能量值的影響，其大小表征了節點i、j的無功電壓耦合程度。一般情況下τij≠τji，考慮到兩節點的電氣耦合對稱性，基于能量信息的無功電壓耦合函數為

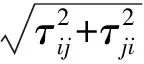
(9)

式中，Sij為節點i、j間的電氣距離，其值反映了節點i、j間的電氣距離大小。Sij越大，對應節點間的電氣距離越小；反之節點間的電氣距離越大。

2 多閾值的分區方法

閾值搜索分區方法是利用圖論的基本理論并結合電力系統的結構特點來研究大系統的結構建模問題。其基本思想是[8]：將系統的變量用圖的節點表示,各變量間的相互關系用連接相應節點的邊表示,各變量間的耦合強度用賦予每一條邊的權重系數表示,從而可將一給定系統用圖的形式表示；然后給定一個門檻值α,消去圖中那些權重小于α的邊,并對完成消去操作后圖的節點進行重新安排,將其中不相連的各個子圖區分出來,則這些子圖實際上就表示相互間的耦合強度小于或等于門檻值α的子系統。這樣,就可將一個大系統分成若干個子系統。

為避免孤立節點的形成并真實地反應電網的實際情況，文獻[10]及文獻[11]提出一種更加符合電網實際運行狀況的多閾值分解法用于電壓控制分區，在理論和實踐應用中取得了較好的效果。為終止搜索過程，根據聚類思想，取分區數量的限制條件為Nmin～Nmax為2～2lnn[10]。

下面利用文獻[11]相關思路分解能量靈敏度矩陣D。其具體算法是對一個n×n階矩陣S進行多閾值分解，由于S是對稱矩陣，只考慮上三角陣：

1)將S中的所有非零元素按其絕對值從大到小排列，得到m1>m2>…>mk；

2)k=1,α1=m1-ε,ε為任意小的正數，利用基本的閾值分解法得到閾值α1下的一種劃分。確定分區個數Nk，若NkNmax就繼續；

3)k=k+1，重復步驟2)至步驟3)，從節點集合中除去已被劃分的節點，由新的閾值劃分剩余的節點子集合，直到分區個數滿足要求為止。

另外，由于電壓靈敏度矩陣的各元素本身體現了電壓對能量的靈敏度信息，在選取區域內主導節點時，可依據區域內各節點在電壓靈敏度矩陣中值的大小確定，即將區域內電壓對能量的變化最敏感者確定為該區域的主導節點。

3 算例仿真

以IEEE 30 、IEEE 118母線系統進行算例分析，以驗證上述分區算法的有效性。

3.1 30節點系統的分區結果

在IEEE 30節點系統的能量靈敏度矩陣中，m1=max(Sij)=0.534 1，ε=0.002。表1給出了在能量電壓靈敏度矩陣下的多閾值分區結果。

表1 ESM下的多閾值分區計算結果

最終獲得的分區結果與文獻[15]的結果對比如圖2所示，圖中實線、虛線分別是表示所提方法和文獻[15]中的方法。

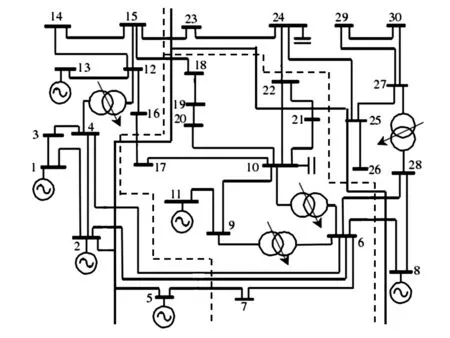
圖2 IEEE 30 節點系統分區結果

圖2顯示了基于ESM的分區結果和文獻[15]的結果的差異。由圖2可看出，兩種分區方法結果基本一致，不同僅存在于對節點5和節點22的劃分。這里將節點5和節點22分別歸于區域2和區域3，而文獻[15]將節點2和節點22分別歸于區域1、2。

事實上仿真結果顯示，電壓能量靈敏度矩陣中S25=0.002 5，S57=0.461 4，表明節點7的電壓波動對節點5將產生更大的影響，節點5和節點7之間的電氣距離更近，節點2電壓波動在節點5處產生的影響較節點7非常有限。因此，區域劃分時應將節點5和7節點劃歸為一個區域。而文獻[15]所劃分的區域1集中了6臺發電機中的4臺，為保證分區后各區域內發電機對本區域內電壓的控制能力，所提方法將5號發電機歸為區域2有其合理性。此外，文獻[7]的分區結果在對節點5的處理上與所提方法一致。從另一側面亦可驗證所提方法結果的正確性。

3.2 118節點系統的分區結果

IEEE 118系統有54個發電機節點和64個負荷節點。利用ESM計算得到的最終分區數為6個，分區結果如圖3虛線所示。

從圖3所示的分區結果來看，利用ESM計算的仿真結果與文獻[16]的基于復雜網絡理論的分區算法及文獻[17]利用的基于慢相關技術的分區結果基本一致。進一步分析區域間相聯各支路的節點能量相關度指標τij發現，各相聯節點間的τij已經非常小。以劃分的區域1、2間的各邊界支路為例，相聯的各支路分別為(8，30)、(17，113)、(17，31)、(16,17)、(14，15),其τij值分別為0.005 9、0.000 5、0.030 8、0.004 8、0.007 3。迭代終止時的閾值為0.0956。這些邊界節點間的τij在迭代終止前依舊遠小于迭代終止時的閾值，說明這些邊界支路的電氣距離很遠，其相鄰節點電壓擾動對本節點的能量影響較小，因此各支路節點間的無功/電壓的相互影響已非常有限。這一結果也說明所提分區方法能保證劃分的區域內部節點聯系緊密，區域外部弱耦合。

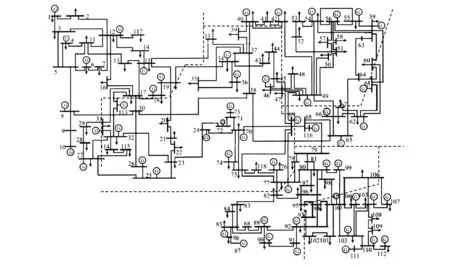
圖3 IEEE 118 節點系統分區結果

3.3 分區時間

算法采用MATLAB 6.1編程實現，在CPU為1.80 GHz、內存1 GB的PC機上運行。計算時間如表2所示(不包括潮流計算的時間，最終計算時間為多次計算后取均值)。

表2 計算分區的時間

所提方法是基于靜態能量函數的數學模型，得到ESM后進行VCR劃分，靜態能量函數的數學模型決定了利用所提算法進行分區的速度優越性。

4 結 論

基于靜態能量函數的數學模型，提出節點相關度指標用于構建系統的能量靈敏度矩陣，基于此，利用多閾值分解法提出一種電壓控制分區的新方法。理論分析和算例仿真結果表明：

1)由靜態能量函數構建的能量靈敏度矩陣能準確地反映各節點間電壓和無功相關的緊密程度。最終劃分的各區域滿足“區域間弱耦合，區域內強聯系”的分區要求，算例仿真的結果表明了該算法的有效性。

2)靜態能量函數的數學模型決定了所提算法在速度上的優越性。特別是在大型網絡分區的計算上時間優勢更加明顯，可望用于分區的在線計算。

3)所提出的基于能量靈敏度矩陣進行VCR劃分的思想概念清晰，無需修改系統的網絡模型，更接近實際運行的系統，較其他算法更易實現。

以上結論為無功電壓控制分區方法提供了新的思路，對維護系統的電壓穩定性具有現實意義。需要說明的是，由于能量函數的數學模型依賴系統的運行方式，其分區結果也取決于系統的運行方式。

[1] 李宏仲，金義雄，程浩忠，等．基于改進粒子群優化算法并計及靜態電壓穩定性的電力系統無功規劃[J]．電網技術，2005，29(22)：50-55．

[2] 盛戈皞，江秀臣．基于多Agent 的二級電壓控制系統的實現及性能分析[J]．電網技術，2005，29(24)：42-48．

[3] 馮光明，陸超，黃志剛，等.基于雅可比矩陣的電壓控制區域劃分的改進[J]. 電力系統自動化，2007，31(12)：7-11.

[4] Schlueter R A, Hu i, Chang M W, et al. Methods for Determining Proximity to Voltage Collapse[J]. IEEE Trans. on Power Systems,1991,6(1):285-292.

[5] Chang C S，Lu L R，Wen F S. Power System Network Partitioning Using Tabu Search[J].Electric Power Systems Research, 1999,49(1):55-61.

[6] 劉大鵬，唐國慶，陳珩.基于Tabu搜索的電壓控制分區[J].電力系統自動化，2002，18(3)：18-22.

[7] 胡澤春，王錫凡，王秀麗，等. 用于無功優化控制分區的兩層搜索方法[J].電網技術，2005，29(24)：37-41.

[8] 范磊，陳珩. 二次電壓控制研究(一)[J].電力系統自動化，2000，24 (12) : 20 - 24.

[9] 方鴿飛，劉君華，呂巖巖．基于樹形分布的電壓控制分區[J]. 電力系統及其自動化學報，2007，19(1)：83-87.

[10] 張忠靜 , 陳 剛 , 關仲,等．基于閾值搜索和動態分散的電壓/無功分區算法[J]. 重慶大學學報(自然科學版),2006,29(12)：52-55.

[11] 丁曉群,黃偉,章文俊,等.基于電壓控制區的主導節點電壓校正方法[J].電網技術,2004,28(14):44-48.

[12] 夏道止.電力系統分析[M]．北京:中國電力出版社，2004.

[13] 劉群英，劉俊勇，劉起方.基于能量信息的電壓穩定性量化指標研究[J]. 電力自動化設備，2008，28(8):8-13.

[14] 鄭武，李華強，陳靜，等．基于靜態能量函數法確定交直流系統最優無功補償點的確定[J]. 電力自動化設備，2010,30(8):45-49.

[15] Mori H, Takeda K. Parallel Simulated Annealing for Power System Decomposition [J]. IEEE Transactions on Power System,1994,9(2):789-795.

[16] 倪向萍，阮前途，梅生偉,等．基于復雜網絡理論的無功分區算法及其在上海電網中的應用[J]．電網技術，2007,9(31):6-12.

[17] Yusof S B，Rogers G J，Alden R T H．Slow Coherency Based Network Partitioning Including Load Buses[J]．IEEE Trans. on Power Systems，1993，8(3)：1375-1382．

Since the energy information can synthetically reflect the reactive injection and the voltage of node bus, a new voltage control partitioning method is proposed based on static energy function and multi-threshold search. With the energy information of node, the node energy correlation degree index (NECDI) is proposed to evaluate the reactive relevance between two nodes. Based on the NECDI, the energy sensitivity matrix (ESM) is established. In the end, the ESM is decomposed to get the voltage control area (VCR) by multi-thresholds search method. Simulation results in IEEE 30 and IEEE 118 bus systems and the comparison with the traditional partitioning method verifies the validity and practicability of the proposed method.

static energy function; energy information; node energy correlation degree index; energy sensitivity matrix; multi-threshold search

TM714

A

1003-6954(2017)05-0005-05

鄭 武(1986)，研究方向為電力系統規劃;

康 勇(1984)，研究方向為計算機網絡。

2017-05-03)